交变载荷作用下焊接接头残余应力释放机理
(上海交通大学 海洋工程国家重点实验室, 上海 200240)
0 引 言
焊接具有经济、高效、便捷的特点,被广泛运用于船舶和海洋平台建造的各个环节。由于焊接是一个瞬间加热再冷却的过程,焊缝附近材料发生不均匀膨胀和收缩,使结构产生变形和残余应力,影响装配精度和结构强度[1]。海洋结构物在波浪环境中频繁遭受交变载荷的作用,容易造成焊缝附近具有较高残余应力区域的应力重新分布,发生应力释放现象[2-4],影响结构的疲劳寿命。本文研究焊缝附近区域焊接残余应力的释放规律,分别对交变载荷作用下垂直和平行于焊缝方向的残余应力的变化特点进行研究,并讨论载荷幅值、应力比等因素对应力释放的影响规律。
1 研究方法
采用顺序耦合热弹塑性有限元法[5-6]计算焊接接头的残余应力和变形,整个过程分为两个步骤:首先,根据特定的焊接条件确定热源模型,考虑材料属性和热分析边界条件,忽略应力场的影响进行焊接温度场计算;其次,将温度场计算结果以载荷的形式作用于力学模型,根据材料力学属性和边界约束条件计算结构的力学响应,得到焊接应力场。在此基础上,采用非线性有限元法研究交变载荷作用下焊接接头的残余应力释放问题,定义材料随动强化模型,施加多工况交变载荷,计算得到焊接接头在不同外载荷作用下的应力场,与焊接初始应力场进行对比,研究残余应力的变化规律。整个分析流程如图1所示。

图1 分析流程图
2 试验设计
2.1 试件尺寸
研究平板焊接接头沿垂直和平行于焊缝方向的残余应力释放问题,忽略沿板厚方向的残余应力。研究对象包括焊缝垂直和平行于交变载荷方向的两种试件,分别测量两种试件位于焊缝一侧的3个测量点沿交变载荷方向的应力。试件材料为Q235钢,外形尺寸相同,具体试件尺寸与测点布置情况如图2所示。试件尺寸为430 mm×140 mm、厚度为3.6 mm,测试段尺寸为160 mm×80 mm,夹持段尺寸为80 mm×140 mm,测试段与夹持段之间通过半径为65 mm的圆弧连接,焊缝长度为80 mm,L1和L2为测点所在直线,测点A、B、C在L1和L2上分别距离焊缝中心线12 mm、20 mm、32 mm和10 mm、18 mm、28 mm。

图2 两种试件的尺寸及测点位置
2.2 焊接和拉伸试验
焊接试验包含3块试件,其中:试件1、2的焊缝垂直于交变载荷方向,用于研究垂直于焊缝方向的残余应力释放规律,焊接速度略有不同,两个试件相互对照以分析偶然误差对焊接试验验证的干扰;试件3的焊缝平行于交变载荷方向,用于研究平行于焊缝方向残余应力的释放规律。焊接采用手工表面堆焊的方式,焊接电流为120 A、电压为25 V、焊丝规格为SH507Φ3.2 mm。分别记录3次焊接的焊接时间和焊缝尺寸,如表1所示,其中焊缝宽度和高度为多次测量的平均值。试件焊接效果如图3所示,方框为焊缝边缘所在位置。

表1 焊接数据记录

图3 试件焊接效果图

图4 电解抛光效果
采用X射线应力测量仪测量试件沿拉伸方向的表面残余应力。在测量前,对试件测试区域进行打磨除锈、电解抛光等表面处理,以防止氧化膜对测量精度产生不利影响。经表面处理后的试件如图4所示。
在焊接试验基础上选取试件1进行单次循环拉伸试验。拉伸试验在MTS试验机上进行,如图5所示。采用准静态加卸载方式对试件进行拉伸,此为线性单次循环载荷,最大拉伸载荷29 kN,加卸载速度为5.8 kN/s,当拉伸载荷达到最大值时,对应试件测试段内的平均拉应力为100 MPa。

图5 拉伸试验过程
3 数值模拟
3.1 有限元模型
通过ABAQUS/standard软件进行数值模拟,根据试件几何尺寸建立三维有限元模型,采用SOLID模型建模[7]。在焊接过程中,热量输入集中在焊缝区域附近,为保证温度场模拟结果的准确性,同时提高计算效率,在温度梯度较大的焊缝及其附近区域采用精细有限元网格,在远离焊缝区域逐渐过渡为较稀疏网格。焊缝垂直于测试段长边方向的试件模型包含67 520个单元和82 794个节点,焊缝平行于测试段长边方向的试件模型包含79 072个单元和95 768个节点。采用3点约束模拟焊接过程中的自由状态,有限元模型及约束条件如图6所示。

图6 有限元模型及约束条件
3.2 模拟结果验证
为验证数值模拟方法的准确性,分别对试件焊后及拉伸后的残余应力测量值和计算结果进行比较。图7为试件焊后沿x轴方向(拉伸载荷方向)残余应力S11的分布云图。试件1、2焊缝中段具有较高的拉应力,首尾端为压应力,由于试件1热输入量高于试件2,因此残余应力数值和高应力区域面积更大;试件3靠近焊缝区域有较高的拉应力,沿垂直于焊缝方向逐渐过渡为压应力,在焊缝横截面上的残余拉压应力保持平衡状态。图8和图9分别为焊接后和拉伸后应力模拟与试验结果对比图。由图8和图9可以看出,焊接、拉伸数值模拟结果与试验结果较吻合,验证了本文采用的数值模拟方法的准确性。

图7 沿x轴方向残余应力分布云图
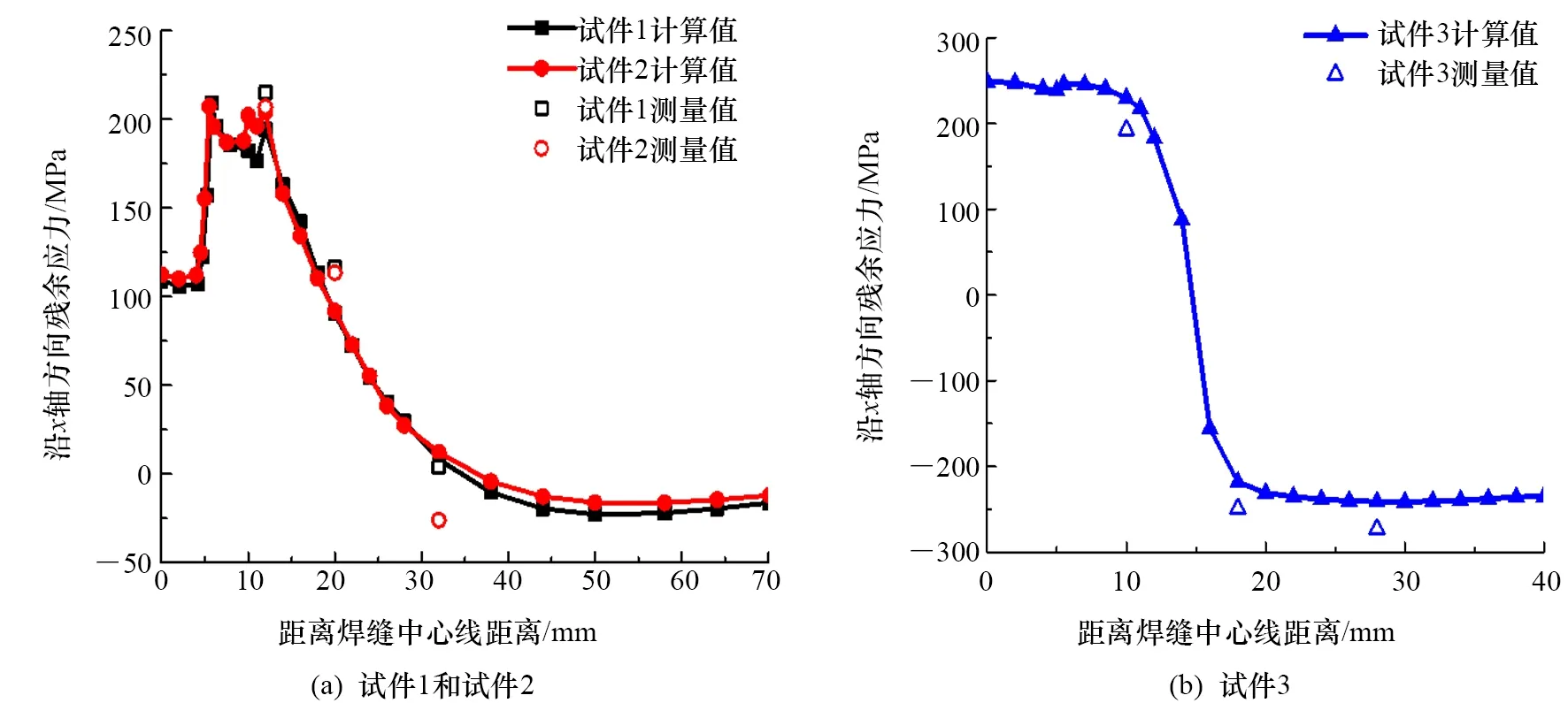
图8 焊接后残余应力测量值与计算结果对比

图9 试件1焊接和拉伸后应力测量值与计算结果对比

图10 载荷幅值为29.0 kN时的加卸载时历曲线
4 应力释放因素分析
4.1 加载幅值对应力释放的影响
为讨论单向拉伸时交变载荷幅值对应力释放的影响规律,选取加载幅值为29.0 kN、43.5 kN、58.0 kN和72.5 kN等4种工况,对应加载达到最大值时试件测试段平均拉应力σa分别为100 MPa、150 MPa、200 MPa和250 MPa。采用准静态线性加卸载方式,循环加载时最小载荷与最大载荷的比值(应力比)为0,周期为10 s,循环次数为10次。载荷幅值为29.0 kN时的加卸载时历曲线如图10所示。
图11为试件1在不同幅值载荷作用下,分别经历1次和10次载荷循环后,L1直线上的点沿x轴方向残余应力的分布情况。从图11可以看出:4种工况下试件均出现应力释放现象,且载荷幅值越高,加载后应力分布曲线偏离原曲线的程度越大,应力释放越明显;1次和10次循环加载后的应力分布曲线完全重合,循环次数对应力释放无明显影响。
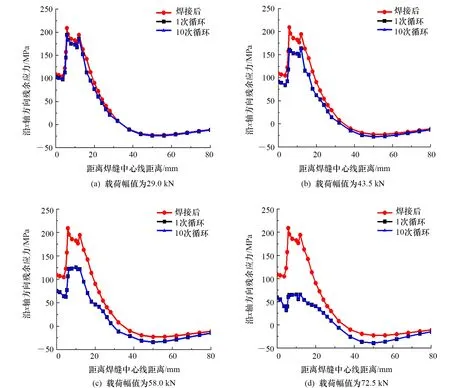
图11 试件1焊接残余应力在不同载荷作用下的分布情况
图11中5~15 mm区域初始残余应力较高,在载荷作用下应力超出屈服强度而产生塑性应变,使得局部区域累积塑性应变增加。图12为载荷幅值为72.5 kN工况下,L1直线上距焊缝中心线12 mm的A点沿x轴方向残余应力和累积塑性应变的时历曲线,可以看出:在第一个循环的加载阶段,A点应力超出屈服强度后产生塑性应变,累积塑性应变增加;当加载达到最大值时,A点应力低于初始残余应力σ0与载荷幅值作用下平均应力σa之和,此时累积塑性应变达到最大值,卸载后应力值σ0′低于σ0,出现应力释放现象;在随后的载荷循环周期内,A点的应力为σ0′与σa的线性叠加,累积塑性应变保持不变,未出现新的应力释放现象。

图12 载荷幅值为72.5 kN工况应力和累积塑性应变时历曲线
将应力变化量与初始应力的比值定义为应力释放率。表2为不同载荷作用下A点累积塑性应变与残余应力释放率之间的关系。当载荷幅值为29.0 kN时,虽然A点累积塑性应变未发生变化,但是附近材料内的应力场发生了改变导致A点应力状态发生变化;随着载荷幅值的增加,累积塑性应变和残余应力释放率逐渐提高;当载荷幅值为72.5 kN时,残余应力释放率达到72.31%,A点的应力显著减小。由图11、图12和表2可见,载荷幅值提高会产生更大的塑性应变,应力释放现象更明显。
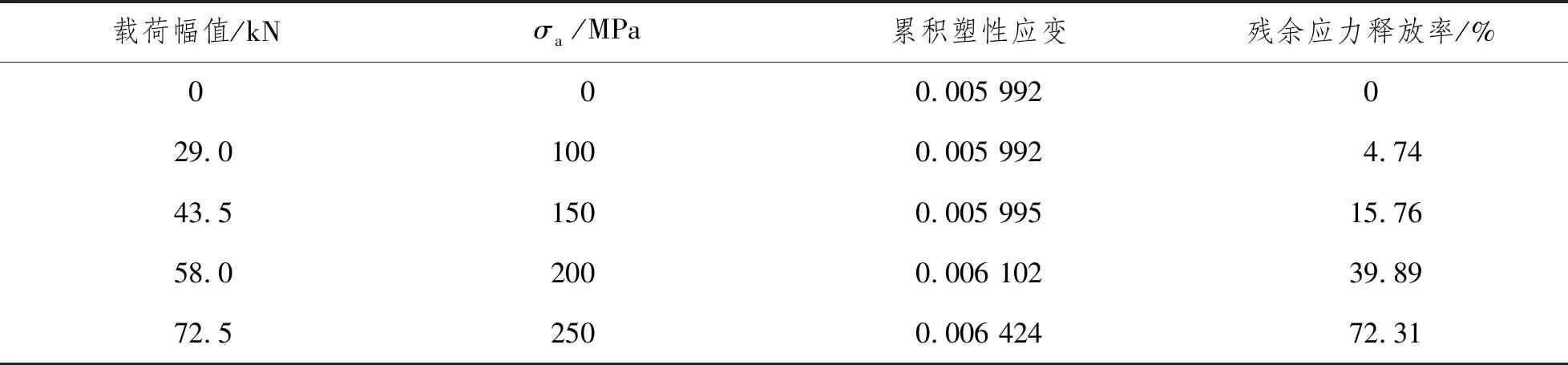
表2 不同载荷作用下A点累积塑性应变与残余应力释放率
4.2 加载顺序对应力释放的影响
为研究加载顺序对应力释放的影响规律,分别对4种载荷幅值采用幅值递增和递减两种加载顺序,即按29.0 kN、43.5 kN、58.0 kN、72.5 kN和72.5 kN、58.0 kN、43.5 kN、29.0 kN的加载顺序,计算A点处残余应力和累积塑性应变。不同加载顺序下的残余应力和累积塑性应变时历曲线如图13所示。由图13可见:当幅值递增时,A点应力在每次加载结束后均出现下降,累积塑性应变在43.5 kN、58.0 kN和72.5 kN等3个加载中出现增加,数值与表2中等幅加载结果一致;当幅值递减时,累积塑性应变仅在第一次加载中出现增加,后续加载对残余应力和累积塑性应变无影响。两种加载顺序最终的应力、应变结果与72.5 kN等幅加载一致,可见应力释放与加载顺序无关,受最大加载幅值影响。

图13 不同加载顺序下残余应力和累积塑性应变时历曲线
4.3 应力比对应力释放的影响
为研究不同应力比对应力释放的影响,选取载荷幅值为66.7 kN(平均应力230 MPa)、应力比分别为0.5、0、-0.5和-1.0等4种情况,计算多次循环后残余应力和累积塑性应变的变化情况。
图14和图15为一次加载循环后L2直线上的点沿x轴方向残余应力的分布情况。从图14可以看出,当应力比为-1.0时,残余应力释放程度更大,其他工况应力分布曲线完全重合。将应力比为-1.0工况的首个加载循环以1/4周期为间隔输出应力数值,如图15所示。从图15可以看出,残余应力在一个周期内经历两次释放过程:第一次发生在0T~0.25T的拉伸加载阶段,高拉应力区域出现塑性应变,发生应力释放现象,其他区域应力值有所降低;第二次则发生在0.50T~0.75T的压缩加载阶段。对比发现,图15中0.50T时刻的残余应力分布与图14中应力比为0.5、0和-0.5等3种工况下的残余应力分布一致,可见在这3种工况下,由于不存在反向加载或反向加载未能超过材料屈服强度,试件仅能在第一个循环的拉伸阶段产生塑性应变,后续加载使试件变形处于弹性范围,对应力释放无影响。
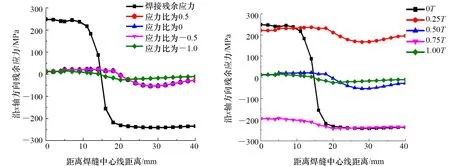
图14 不同工况残余应力分布情况 图15 应力比为-1.0时不同阶段残余应力分布情况
当应力比为-1.0,正、反向加载达到最大值时,测试段均能产生230 MPa的平均应力,由于包辛格效应[8],材料一个方向屈服强度的提高会使反向加载屈服强度降低,试件上存在一点由于拉伸发生硬化导致压缩时屈服强度低于230 MPa,在循环载荷作用下产生持续的塑性应变。选取距L2直线45 mm、距焊缝中心线13 mm、初始残余应力为31.8 MPa的D点,该点在拉伸、压缩两个加载阶段均会超过屈服强度产生塑性应变,累积塑性应变不断增大,如图16所示。
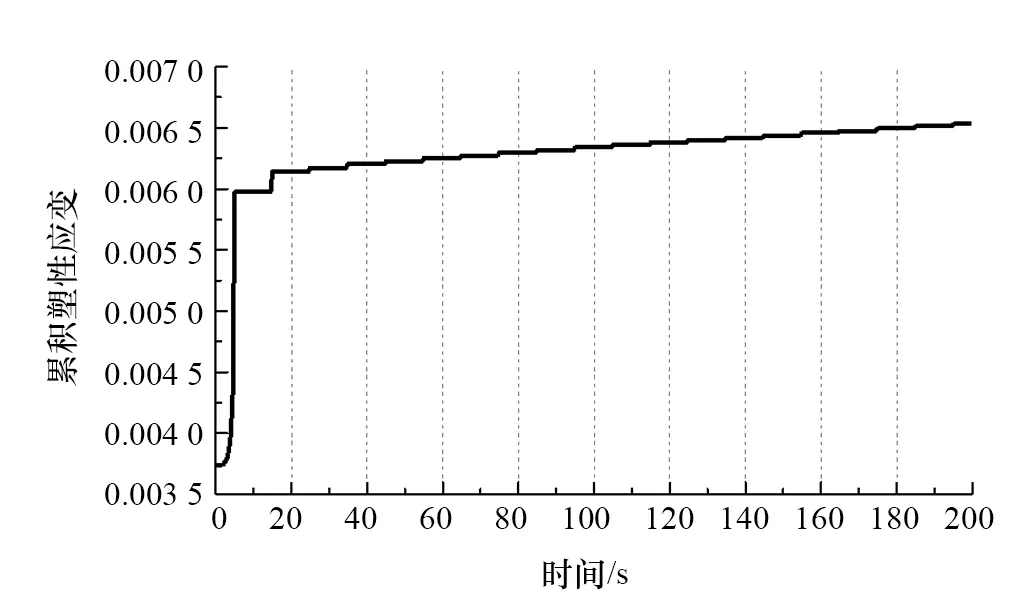
图16 累计塑性应变时历曲线
表3为D点沿x轴方向残余应力在每个循环末的数值。从表3可以看出:在第一个循环后该点由拉应力变为压应力,应力数值明显降低,后续循环使该点压应力数值略有提高,在2~10次循环后残余应力变化量与初始值的比为0.092 8,在11~50次循环后比值变为0.023 6。可见持续的塑性应变会引起应力的持续释放,然而循环次数的增加对应力释放效果的影响迅速降低。

表3 每个循环末横向残余应力数值
5 结 论
采用数值模拟方法研究载荷幅值、应力比等因素对焊接接头残余应力释放的影响规律,主要结论如下:
(1) 在单向加载时,残余应力释放程度与加载最大幅值有关,与加载顺序和周期数无关。
(2) 当存在反向加载但加载幅值较小时,试件无法在反向加载阶段再次产生塑性应变,应力释放效果与仅拉伸的工况相同;当反向加载幅值较大时,试件会出现持续的应力释放现象,第一个加载周期对应力释放起主要作用。
(3) 累积塑性应变的增加是产生应力释放现象的关键因素,提高残余应力释放率需要从有效增加相关区域塑性应变的角度考虑。

