Nonlinear Numerical Simulation for Flexible Pipes Carcass Wet Collapse
-,-,-
(Naval Architecture and Ocean Engineering R&D Center of Guangdong Province,South China University of Technology,Guangzhou 510641,China)
Abstract:As a typical failure mode of flexible pipes,it is essential to investigate the carcass collapse.Considering the influence of an inner sheath layer, the carcass wet collapse finite element model with an inner sheath layer was created in this paper.Nonlinear numerical simulation of collapse behavior is carried out based on the arc-length method. The influence of the initial ovality, contact nonlinearity and material nonlinearity on carcass collapse characteristics is systemically investigated. Moreover,the results were also compared with those of the pure carcass collapse model without an inner sheath layer under the same condition. The research results indicate that the critical collapse load decreases with the increase of initial ovality,which shows a negative correlation.It will have a great influence on the critical collapse load considering the contact nonlinearity and material nonlinearity. And the specific performance is that the critical collapse load will increase with the increase of frictional coefficient and the yield stress of material, which shows a positive correlation. The critical collapse load increases slightly considering the influence of inner sheath layer,which shows that the inner sheath layer plays a role on bearing the external pressure,but has little influence on the carcass critical collapse load.
Key words:flexible pipe;carcass;collapse failure;nonlinear numerical simulation
0 Introduction
Flexible pipes have been widely applied in the marine oil and gas field due to their superior mechanical properties and convenience in transportation and installation. The structure of flexible pipes is complex since they are composed of many metal layers and polymer layers,each of which has their own function. Carcass, the innermost layer of flexible pipes, is used to bear the outer pressure and prevent the collapse failure. The collapse can be classified into the wet-collapse and dry-collapse. In the wet-collapse, it is assumed that when the outer sheath layer is damaged, the water will enter the annulus area, and inner sheath layer and carcass will bear all outer pressure. Thus the wet-collapse is a more dangerous failure condition compared with the dry-collapse.Therefore,the investigation of the carcass wet collapse is of great significance.
Some scholars studied the collapse behavior of flexible pipes and also obtained some important results. As for the analytical calculation, most scholars assume that the cross section of the flexible pipes is equivalent to a homogeneous cylinder, and then solve the critical collapse load based on the Timoshenko elastic stability theory[1]. Generally, there are four equivalent methods used at present. Zhang et al[2]made use of cross section area equal method to simplify the carcass to a homogeneous cylinder and then get the critical collapse load. de Sousa et al[3]took unit area bending stiffness equal method and assumed that the unit area bending stiffness is equal between the initial model and equivalent model. Neto et al[4]took the same bending stiffness equal method, but assumed that the bending stiffness of unit axial length is equal between the initial carcass and equivalent cylinder. In addition, Tang et al[5]proposed the strain energy equivalent method to transform a Representative Volume Element (RVE) of the carcass layer into a homogeneous shell with an equivalent thickness. Although the theoretical methods are easy to operate, the simulation results by different equivalent methods differ significantly.On the other hand, only the critical collapse load under ideal condition can be obtained by the analytical method, because the method cannot take into account the influence of carcass geometric defects, contact conditions and material nonlinearity. Thus some of scholars used some numerical analysis tools to analyze the carcass collapse. Neto et al modeled two carcass collapse finite element models, the carcass lay angle was considered respectively and ignored in the two models. The results show that the carcass lay angle has little influence on the critical collapse load and the theoretical methods cannot accurately predict the critical collapse load[6]either. The similar conclusions were also drawn by Cooke[7]. Nogueia et al presented a simplified numerical model based on beam element. Although it is convenient for calculation, the result is inaccurate due to the hypothetical restriction of element itself[8].Loureiro Jr and Pasqualino[9]evaluated the collapse behaviors of flexible pipes under combined bending and external pressure,and thought it was more practical with respect to collapse under curved pipes.Tang et al[10]ignored the carcass lay angle and established the quarter carcass finite element model based on ANSYS software. It is concluded that the pipe initial ovality and materials elasticplasticity will have a great impact on the critical collapse load. However, the effect of inner sheath layer on collapse characteristics is not considered.
Due to the fact that the theoretical method cannot consider the influence of carcass geometric defects,contact conditions and material nonlinearity,the finite element numerical analysis method is adopted in the paper and the carcass collapse numerical model is created by ABAQUS software. Since the FE models in the literature contain only carcasses, the influence of an inner sheath layer is taken into account in this paper and the collapse model is built with the carcass and inner sheath layer included.Based on the created FE models,the nonlinear numerical simulation for flexible pipes carcass collapse was done and the influence of the initial ovality, contact nonlinearity and material nonlinearity on the carcass collapse characteristics is investigated. Moreover, the results are also compared with those of the carcass collapse model without an inner sheath layer.
1 Pipeline collapse theory
The theoretical method for solving the pipeline critical collapse load is mainly based on the classical Timoshenko elastic stability theory[1].Timoshenko analyzed the elastic collapse instability of the annulus structure in detail in his work. And he assumed that the radial deflection is small deformation and the tangential direction of the thin rod is neglected in the derivation process.

whereωis the deflection of a circular ring,θis the circular angle,Mis the moment on the circular section,EIis the bending stiffness on the circular section, andRis the ring curvature radius.
Assuming that the plane ring is subjected to uniform external pressureq, the analytic solution of the elastic instability can be obtained based on Eq.(1).As shown in Fig.1,assuming that there is initial maximum radial deflectionω1, thus the initial displacement at the other section of the ring can be expressed asωi=ω1cos(2θ). The radial displacement is recorded asωunder the uniform outer pressureq, thus the bending moment at any cross section can be expressed as:
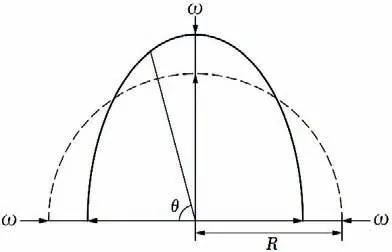
Fig.1 Schematic diagram of plane ring with initial imperfection

Substituting Eq.(2)into Eq.(1),the following is reached
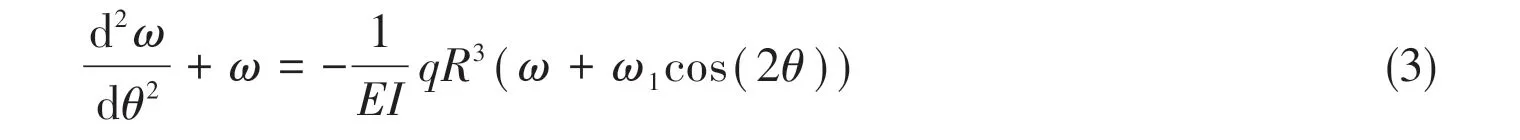
Based on the boundary continuous conditions of differential equation at the points A, B, C and D,the analytical solution of Eq.(3)can be obtained.

Eq.(4) is just the analytical expression for the radial displacement of a plane ring elastic buckling under uniform external pressure.qcris the first-order critical collapse load of a plane ring.

For the case of rectangular ring cross section,the bending stiffness can be further expanded and the critical collapse load formula can be obtained.

wheretis the thickness of the plane ring.

Tab.1 Equivalent thickness calculating methods
The real carcass cross section is complex.As a result,the key point is how to get the equivalent thickness of carcass cross section in order to use Eq.(6) for solving the critical collapse load.It is mentioned above that there are four main thickness equivalent methods.These equivalent thickness calculating methods are shown in Tab.1. It should be noted that although there are the four main thickness equivalent analytic methods,the consistent conclusion for the accuracy of different methods was not obtained. Moreover, the analytic method cannot take into account the influence of carcass geometric defects,contact conditions and material nonlinearity.
2 Collapse numerical model
The disadvantage of the theoretical method in evaluation of the collapse behavior mentioned above is that the influence of contact nonlinearity and material nonlinearity is ignored.Thus the finite element tool is chosen to simulate the carcass collapse in the paper.
2.1 Geometric parameters and material properties
Based on the model set-up in Ref.[6], the numerical collapse model having the carcass and inner sheath layer is established. Fig.2 shows the carcass cross section shape. Tab.2 and Tab.3 show the detailed carcass geometric and material parameters, respectively. The inner sheath layer geometric and material parameters are shown in the Tab.4.
The carcass lay angle has little influence on the critical collapse value under uniform external pressure[6-7].Therefore,the carcass lay angle is not considered in the model creation.Considering the symmetry of structure at the same time, the 2-pitch quarter carcass collapse numerical model was established as shown in Fig.3.
Fig.2 Carcass cross section shape

Tab.2 Carcass cross section parameters

Tab.3 Carcass geometric and material parameters

Tab.4 Inner sheath layer geometric and material parameters

Fig.3 Carcass collapse finite element model

Fig.4 Diagram of boundary condition and load
2.2 Boundary condition and load
Fig.4 shows the scheme of model boundary condition and load. The displacement ofXdirection is limited atX=0 and the displacement ofYdirection is limited atY=0. At the same time,a node freedom degree at the end is restricted in theZdirection in order to avoid axial displacement of rigid body. As for the load application, the outer pressure directly exerts on the outer surface of the inner sheath layer.
2.3 Contact and nodes coupling
The red lines in Fig.5 denote the contact position of the carcass with respect to inner sheath layer and the adjacent surfaces of carcass.The carcass collapse behavior under different contact conditions was analyzed in the paper, including bonded contact, surface to surface frictional contact and frictionless contact.The detailed analysis results are reported in Section 3.2.

Fig.5 Contact between layers and nodes coupling
Some nodes need to be coupled in order to set up the cyclic symmetric boundary conditions and ensure the same pitch. Four groups of coupling nodes, A1-A2, B1-B2, C1-C2 and D1-D2, were arranged as shown in the Fig.5. The equation coupling method in ABAQUS was chosen to ensure equal freedom degree inX,YandZdirections.
3 Results and discussion
3.1 Eigenvalue buckling analysis
The carcass eigenvalue buckling analysis is firstly carried out without considering the initial ovality defect and material nonlinearity to obtain the critical collapse load. The load is regarded as the input value of the external pressure load for the next nonlinear buckling analysis. The first order eigenvalue buckling results are focus at present. Thus the eigenvalue extraction number is set as 1 and the calculated first order eigenvalue is 67.137. The eigenvalue of 67.137 means that the carcass critical collapse load under the eigenvalue buckling analysis is 67.137 MPa.The carcass first-order eigenvalue buckling mode is shown in the Fig.6.It can be seen that the carcass first buckling mode is elliptical.

Fig.6 Carcass first order eigenvalue buckling mode
3.2 Nonlinear buckling analysis
Based on the eigenvalue buckling analysis results, the arc length method is used to analyze the carcass nonlinear buckling characteristic by considering the large deformation and nonlinear options. The load-displacement curves under different conditions are obtained, among which the ordinateUis the displacement and the coordinate LPF is just the load proportionality factor.It can be found that the displacement changes very little with the outer pressure increasing at the initial stage of the curves. With the increase of outer pressure, the carcass buckling failure occurs, where a small load increment will cause a large displacement change. Thus the corresponding transverse coordinate value right now can be set as the critical collapse load.
3.2.1 Collapse characteristics under different initial ovality
The real carcass usually has a certain initial ovality due to the influence of manufacturing error and the radial compression in the pipeline installation process. Thus it is necessary to study the effect of this geometric defect on the carcass collapse characteristics.
The formula for calculating ovality defined by API(American Petroleum Institute)is[12]:

whereDmaxandDminrepresent the maximum and minimum inner diameter,respectively.
The carcass collapse characteristics under the initial ovality of 0.2%, 1%, 2% and 3%were analyzed in this paper, of which 0.2% is the default initial ovality from the specifications of API Recommended Practice for Flexible Pipe[12]. The contacts between layers and between strips are set as bonded and the material is regarded to be linearly elastic. The application of initial defect ellipticity is based on the deformation of eigenvalue buckling analysis, and the modal scaling factor is adjusted in the Risk analysis.The initial ovality is applied by changing the modal scaling factor in the Risk analysis of ABAQUS based on the deformation results of eigenvalue buckling analysis. Fig. 7 shows the collapse curves (load-displacement curves) under different initial ovalities. Tab.5 shows the critical collapse values under different initial ovalities according to Fig.7. It can be found that the carcass critical collapse load shows small amplitude reduction with the increase of the initial ovality.
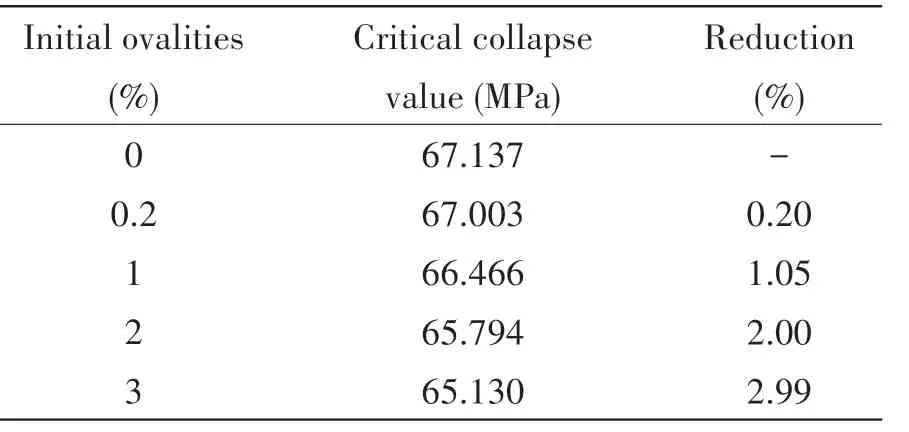
Tab.5 Critical collapse values under different initial ovalities
3.2.2 Collapse characteristics under contact condition
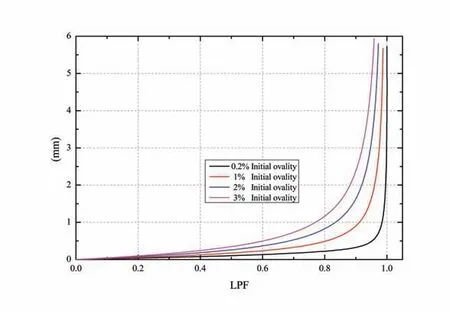
Fig.7 Load-displacement curves under different initial ovalities
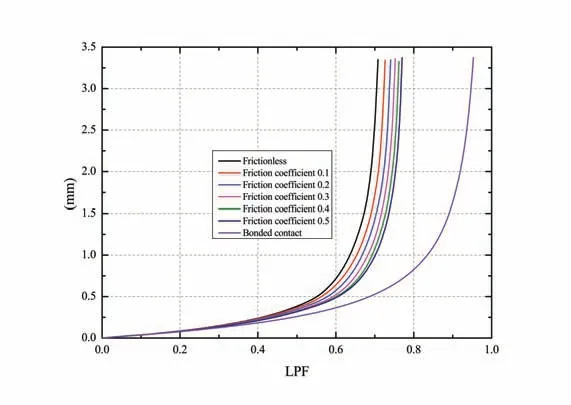
Fig.8 Load-displacement curves under different contact conditions
Based on the analysis results above,with the initial ovality set as 2%,the carcass collapse characteristics under different contact conditions were analyzed. Three kinds of contact conditions including bonded contact,frictional contact and frictionless contact were considered to analyze the impact of contact nonlinearity on the carcass collapse behavior.The contact tangential behavior was simulated by Coulomb friction model with the frictional contact and the friction coefficient set respectively at 0.1 to 0.5. Fig.8 shows the collapse curves (load-displacement curves)under different contact conditions.Tab.6 shows the critical collapse values under different contact conditions according to Fig.8.It can be found that the carcass critical collapse value reduces greatly considering the contact nonlinearity, and the carcass critical collapse value increases with the increase of the friction coefficient.

Tab.6 Critical collapse values under different contact conditions
3.2.3 Collapse characteristics considering the material nonlinearity
The materials of carcass and inner sheath layer above were considered to be in the linear elastic stage.But the real carcass and inner sheath layer would have obvious elastoplastic deformation under the real working state,which may have a pronounced influence on the carcass collapse behavior.Thus it is necessary to investigate the collapse characteristics under the material elastoplastic condition. The carcass material stress-strain relationship is described by the Ramberg-Osgood equation with the yield stress set to be 320 MPa and 420 MPa, respectively[11].The carcass material stress-strain curve is shown in Fig.9.For the internal sheath layer,a multi-linear elastic material model was selected, Fig.10 shows the material stress-strain curve of internal sheath layer.

Ramberg-Osgood equation:whereεis the strain,σis the stress,Eis the modulus of elasticity,σyis the yield stress,c1andc2are 3/7 and 10,respectively.
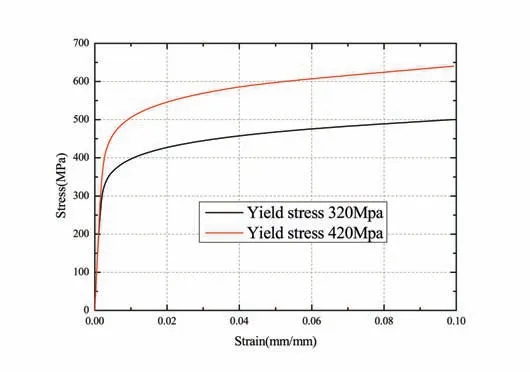
Fig.9 Carcass material stress-strain curves
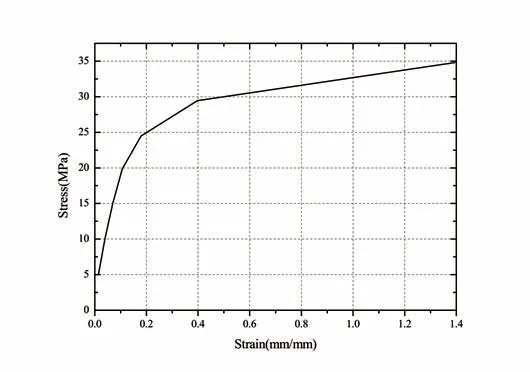
Fig.10 Inner sheath layer material stress-strain curve
The initial ovality was set as 2% and the contact condition was set as frictional contact with a frictional coefficient of 0.2.Then the carcass collapse characteristics considering the material nonlinearity were analyzed. Fig. 11 shows the collapse curves (load-displacement curves) considering the material nonlinearity. Tab. 7 shows the critical collapse values considering the material nonlinearity according to Fig.10. It can be found that the carcass critical collapse value reduces greatly considering the material nonlinearity. Moreover,the carcass critical collapse value increases with the increase of the yield stress.
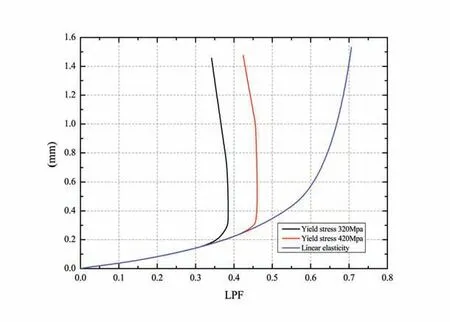
Fig.11 Load-displacement curves considering the material nonlinearity

Tab.7 Critical collapse values considering the material nonlinearity
4 Comparative analysis between models with and without an inner sheath layer
To investigate the function of an inner sheath layer for bearing the outer collapse load, the carcass collapse model without an inner sheath layer (Model I)was created to compare with the model with an inner sheath layer (Model II). The collapse characteristics under three kinds of conditions between the two models were analyzed and the collapse curves (load-displacement curves) are shown in the Fig.12. It can be found that the critical collapse values slightly increase considering the influence of the inner sheath layer,which indicates that the inner sheath layer plays a role on bearing the outer collapse load, but it has little influence on solving the carcass critical collapse value.
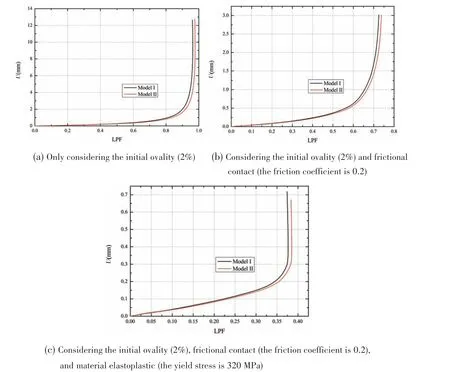
Fig.12 Comparison of collapse curves between Model I and Model II under different conditions
5 Conclusions
The carcass wet collapse model including an inner sheath layer was modeled in this paper,and the influence of the initial ovality,contact nonlinearity and material nonlinearity on the carcass collapse characteristics was also considered separately.Moreover,the comparison between the model with an inner sheath layer and the pure carcass model without an inner sheath layer was carried out.The following conclusions are reached:
(1) The initial ovality will reduce the collapse resistance of the pipeline, thus the carcass initial ovality should be limited as much as possible during the manufacturing and installation process.
(2) The contact condition and material nonlinearity have a great influence on the carcass critical collapse load, which should be taken into consideration in pipeline design process. The specific performance is that the critical collapse load decreases greatly when considering the friction contact and the material elastic-plastic.The critical collapse load increases with the increase of the friction coefficient and the critical collapse load also increases with the increase of the yield stress.
(3) The critical collapse load increases slightly considering the influence of an inner sheath layer, which shows that the inner sheath layer plays a role on bearing the outer collapse load,but it has little influence on the carcass critical collapse load.
- 船舶力学的其它文章
- Effective Elastic Modulus Characteristics of Buoyancy Materials of Full-ocean-depth Manned Submersible
- Fatigue Strength Assessment of Welded Joints Using Strain Energy Density Method Based on NSIF
- Hydrodynamic Analysis of a Spar Platform under Asymmetrical Mooring System
- Effects of Inflow and Outflow of Floodwater on the Parametric Roll of a Damaged Ship
- Analysis of Drilling Riser in Re-entry Operation Under Complex Currents
- Numerical and Experimental Study for SCR with Cable3D

