基于PSO的SVR模型在多联机功耗预测上的应用

李昱瑾1 陈焕新 刘江岩

(1 华中科技大学中欧清洁与可再生能源学院 武汉 430074； 2 华中科技大学能源与动力工程学院 武汉 430074)

变制冷剂流量的多联机空调系统[1]相对于传统的集中空调系统具有系统设置、安装维修、使用管理、适应负荷变化等多方面的灵活性及控制系统选择的多样性等优点。可广泛适用于中小型建筑物的空气调节，或较大型建筑物基于使用功能需要分区进行空气调节、空调运行时间不统一的系统中[2]。

在能源有限的前提下，保证建筑舒适度的同时，如何有效降低建筑物空调系统能耗成为目前重要的研究内容。多联机空调系统作为主流空调系统之一，对其能耗进行预测分析在能源管理、运行策略优化、控制优化等方面均有重要的意义。

现代智能预测技术是指利用计算机对历史数据进行自主学习、智能构建预测模型的方法。支持向量机[3-4]是目前基于统计学习理论的机器学习方法中比较新的理论成果，凭借训练样本小、泛化能力好、实用性强等优点，能较好地解决陷入局部最优、非线性等问题，在能耗预测方面优势突出。

从能耗预测技术[5-6]在行业内的发展情况而言，基于支持向量机的能耗预测模型也是当前的主流选择。刘江岩等[7]分别建立了支持向量回归(support vector regression，SVR)、BP神经网络(back propagation neural network，BPNN)、决策树(classification and regression tree,CART)三种预测模型对地铁站内环境温度进行时序性预测。结果表明基于SVR的时间序列预测模型精度比BPNN和CART更高。魏来[8]在区域建筑能耗的预测中,发现运用支持向量机模型和自助多元自适应回归样条法的预测效果最好。Han Xinyu等[9]建立了一种粒子群优化算法PSO(particle swarm optimization)-SVR温度补偿模型，来改善压力传感器受温度漂移影响而造成的精度和可靠性下降的问题。通过优化SVR的惩罚系数C和核参数γ，改善了粒子陷入局部最小值的问题，预测结果表明PSO-SVR模型的补偿精度高，效果优于径向基(radial basis function，RBF)网络和支持向量机(support vector machine, SVM)。叶小岭等[10]运用基于非线性递减惯性权重和自适应变异的粒子群优化(adaptive mutation particle swarm optimization,AMPSO)支持向量机(AMPSO-SVM)方法对湿度传感器进行温度补偿，并与遗传(genetic algorithm,GA)支持向量机(GA-SVM)和标准粒子群支持向量机(PSO-SVM)优化方法进行了对比。结果表明：AMPSO-SVM模型预测相对误差绝对值均在3%之内，同时仅在25步迭代之后就达到了最优值，相比于其他方法有抗早熟能力强、搜索精度高、收敛速度快的优点。李丹等[11]针对标准粒子群优化(PSO)算法存在易陷入局部极值点的缺点，提出了一种基于物种概念的动态多种群粒子群优化算法(dynamic multi-particle swarm optimization,DMPSO)，经DMPSO优化SVM模型参数，并利用快速傅立叶变换(FFR)进行频谱分析来确定SVM的输入量。电力系统短期负荷预测的实际算例表明，与传统预测方法相比，该方法具有更高的预测精度和鲁棒性。Fan Guofeng等[12]提出一种新的基于支持向量回归(SVR)的负荷预测模型，对于高频数据集，利用具有全局寻优能力的粒子群算法(PSO)来确定SVR模型的3个参数，通过对比不同竞争预测模型之间的性能，验证了该模型具有预测精度高、鲁棒性强的优点。对于多联机系统，研究大多集中在其性能的提高和与其他HVAC系统的对比分析上，但对多联机系统的功耗评估关注很少，因此本文以多联机系统功耗作为主要研究对象。另外，通常使用SVR模型进行预测研究时，模型参数选择一般采用网格搜索和交叉验证相结合的方法，网格寻优步长选取过大或过小会造成模型预测精度低或优化运算时间过长的问题，实际应用效果不理想。

本文引入PSO算法来改善SVR模型的模型参数，提高求解效率并获得更精确的解，从而提高SVR预测模型对多联机系统功耗的预测精度和稳定性。图1所示为研究流程。

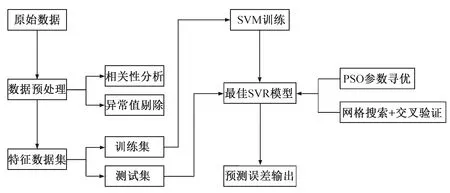
图1 研究流程

1 PSO-SVR能耗预测模型

1.1 SVR模型

支持向量回归方法基本思路为：在训练数据集有限的条件下，建立输入与输出之间连续的函数关系，使预测误差尽可能小并保证回归函数的平滑性。

针对多联机系统，支持向量回归问题可以描述为：对于实验获得的多联机系统运行数据集H，假设其目标预测变量“总功率”与其他测量的相关变量x={x1,x2,…,xi}之间存在f(x1,x2,…,xi)=WHx+b的函数关系，其中，W为权重系数向量，b为偏置项。本文目标是通过数据分析建模来拟合多联机系统的“总功率”与其他相关变量之间存在函数关系。即多联机系统的能耗预测问题转化为对回归函数f(x1,x2,…,xi)=WHx+b的拟合问题。如果要得到较高精度多联机系统能耗的预测结果，则必须提高回归函数的拟合精度。应用SVM进行回归分析时，需要引进核函数将输入空间通过非线性映射的方式转化到高维的特征空间中并对其进行线性处理，根据核内积并以不敏感损失函数ε为准则，得出非线性的拟合模型并使其间隔最大。从而使回归函数f(x1,x2,…,xi)的精度达到最大，得到最优的多联机系统能耗预测结果。

1.2 PSO算法

粒子群优化PSO算法是一种随机搜索算法，他能以较大的概率收敛并得到全局范围的最优解。在动态的、多目标的优化问题中，相比传统优化算法，PSO算法具有更快的搜索速度以及避免陷入局部最优的能力。相比遗传算法，PSO算法没有其复杂的种群交叉和变异操作，保留了基于全局的搜索策略。因此，应用PSO算法到本文的多联机系统的SVR能耗预测模型参数优化中，也能为问题的解决提供很好的帮助。

PSO算法[13-15]的概念可以简单地从这样一个生物学的场景来类比：有一群鸟在一块特定的区域搜索食物，在这个区域内只有一块食物，但是这些鸟并不知道食物的具体位置。这些鸟在寻找食物的过程中，不断地根据可能发现食物位置的鸟提供的信息，改变自己的位置和飞行速度，以求更接近食物的位置。显然，寻找到食物最优的策略就是在目前离食物位置可能最近的鸟的周围区域进行搜索。

对于本文所研究的多联机系统SVR能耗预测模型的参数寻优问题，参数惩罚系数C、核参数γ的最优解就相当于上述场景中的两块食物，而每一只鸟就是我们寻求最优解的工具——“粒子”。而迭代运算就在这些鸟不断缩小食物所在位置的搜寻范围的过程中得以体现。

主要算法内容：对于由n个粒子组成的粒子群，在本文所需要解决的多联机系统SVR能耗预测模型的双参数寻优问题空间中，每个粒子都需要完成搜寻目标参数C和γ最优位置的取值任务，并将每一次迭代所求的最优解带入多联机系统SVR能耗预测模型的回归函数中进行均方误差(mean square error,MSE)分析，直至模型回归函数的MSE达到全局最优，将对应的搜索解输出为全局最优解，得出多联机SVR预测模型的参数寻优结果。

每个粒子在每一次迭代完成后，所处的位置可以表示为xi=(xi1,xi2,…,xiD)，此刻对应的速度可以记为vi=(vi1,vi2,…,viD)。对粒子群体进行更新即迭代运算时，其速度和位置的更新公式如式(1)和式(2)所示：

vid(t+1)=ωviD(t)+c1r1[piD(t)-xiD(t)]+c2r2[pgD(t)-xiD(t)]

(1)

xiD(t+1)=xiD(t)+viD(t+1)

(2)

式中：ω为惯性权重，用于控制粒子飞出多联机系统SVR模型参数寻优的问题空间、群体“爆炸”现象的发生；r1和r2为[0,1]之间的随机数；c1和c2为学习因子，代表粒子自我总结和向群体中优秀个体学习的能力；pi和pg分别为当前时刻局部搜索(即每个粒子的)最佳位置和全局搜索(即所有粒子的)最佳位置。对于每个粒子的速度的取值范围还需加以限制，以控制搜索的快慢来控制其搜索精度。

图2所示为PSO-SVM的算法流程。

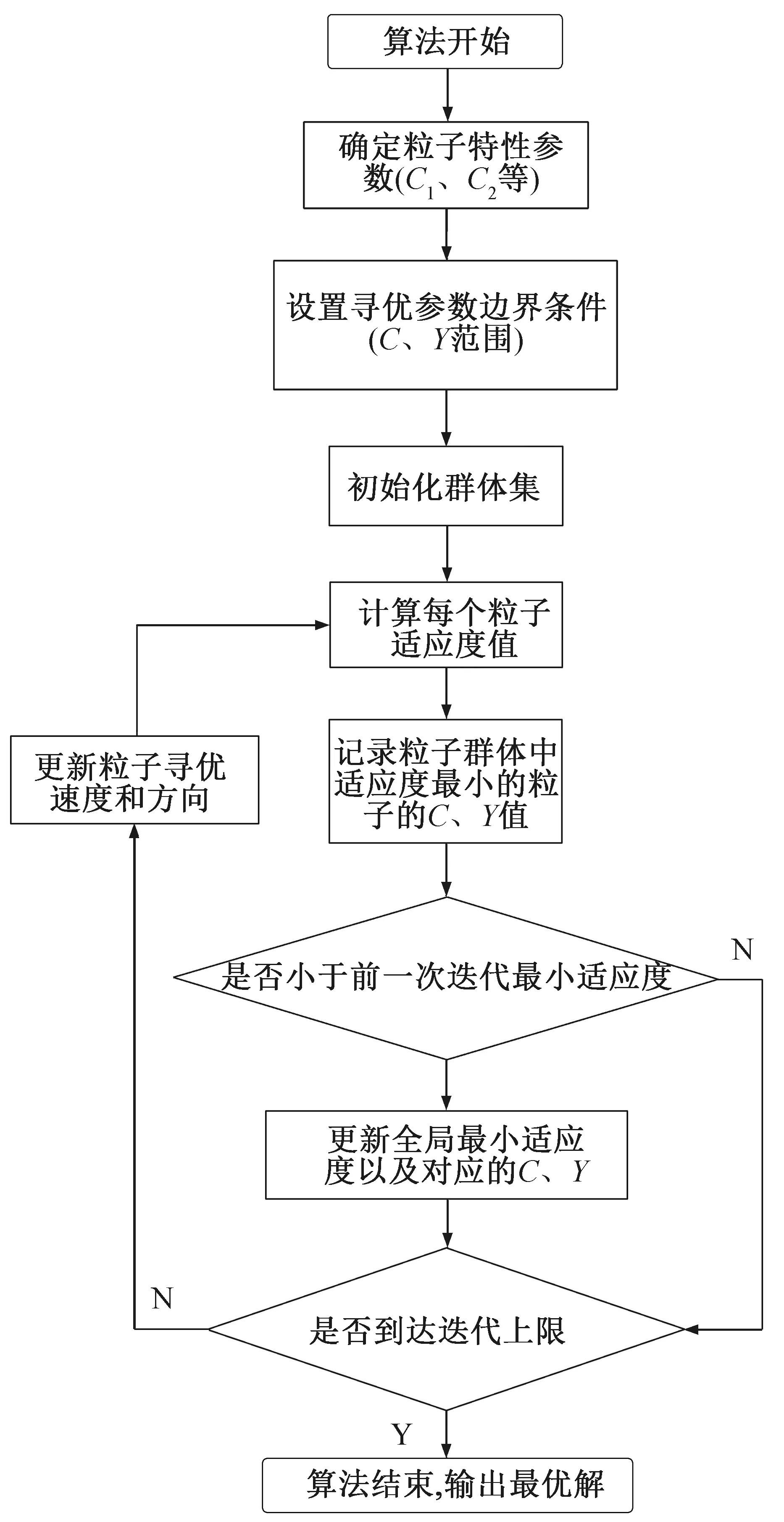
图2 PSO-SVR算法流程图

2 实验数据来源

2.1 多联机能耗数据采集及特征分析

图3所示为多联机(variable refrigerant flow，VRF)系统的结构。根据研究的多联机系统能耗预测问题的需要，在相应机组位置设立传感器来采集可能需要的各类多联机系统运行参数，各传感器位置如图3所示。室外机组额定制冷量为28 kW，室内机组额定制冷量为2.8、3.6、5.0、7.1、11.2 kW。制冷剂为R410A，名义充注量为9.9 kg，压缩机为全封闭涡旋式压缩机。

实验前已经对多联机系统和各测量仪器进行故障排查，保证各机组部件都能正常有效的运行。实验时设定制冷剂充注量占比为95.75%进行机组测试，记录的实验数据包含室内/外温度、压缩机运行频率、排气温度、模块温度、壳顶温度、母线电压及电流、模块高压、模块低压、化霜温度、过冷器液出温度、过冷器气出温度、气分进管温度、气分出管温度、室外机EXV、过冷器EXV、总功率，共18个参数，最终获得1 869组实验数据。

实验采集的多联机系统运行参数共有18个，除去研究的目标变量“总功率”，剩余的参数数量过多。针对多联机系统的功耗问题，应选取与机组自身相关的变量参数作为研究变量。这些变量中，并非所有的参数都对“总功率”的变化产生影响，或者相对其他参数对“总功率”的影响具有独立性。因此，需要对原始的多联机实验数据集进行数据的特征分析，来确定对“总功率”的变化趋势影响相对较显著的几个变量，并把这些变量的数据和“总功率”作为最终的针对能耗预测模型研究的数据集。将原始多联机运行数据集中所有的测量参数与“总功率”作相关性分析，对筛选出的与多联机机组相关13个参数分别用字母A到M进行指代，依次为：A-压缩机运行频率、B-压缩机排气温度、C-压缩机壳顶温度、D-化霜温度、E-过冷器液出温度、F-过冷器气出温度、G-气分进管温度、H-气分出管温度、I-室外机制热EXV、J-过冷器EXV、K-压缩机电流、L-压缩机模块温度、M-总功率。相关性分析结果如图4所示。

表1所示为与总功率M相关性较强的特征变量的相关性系数。将图4中相关性明显较强的4个运行参数选为预测模型的特征变量。

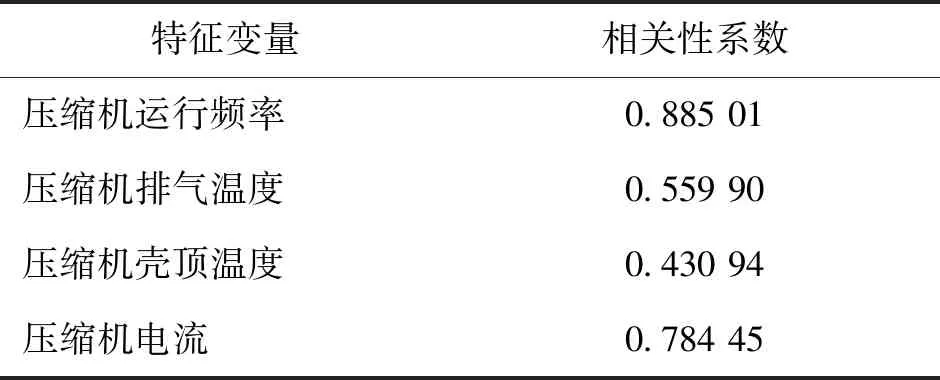
表1 特征变量的相关性系数

2.2 多联机系统SVR能耗预测模型

采用“总功率”和与其相关性最强的7个变量的实验数据(相关性系数绝对值大于0.35)作为预测模型的训练数据。由于采集的多联机系统运行数据不具备时序性的特征，在划分训练集和测试集时可采用随机种子方法，按训练集占总数据80%，其余数据作为测试集的比例进行数据随机分组。

SVR能耗预测模型核函数选择普适性良好的高斯径向基函数，模型设计参数网格寻优结果为惩罚系数C=10，核参数γ=0.25。测试集的预测结果评价情况如表2所示，MAE(mean absolute error)为平均相对误差，MSE(mean square error)为平均均方误差，RMSE(root mean square error)为均方根误差，MAPE(mean absolute percentage error)为平均相对百分误差。

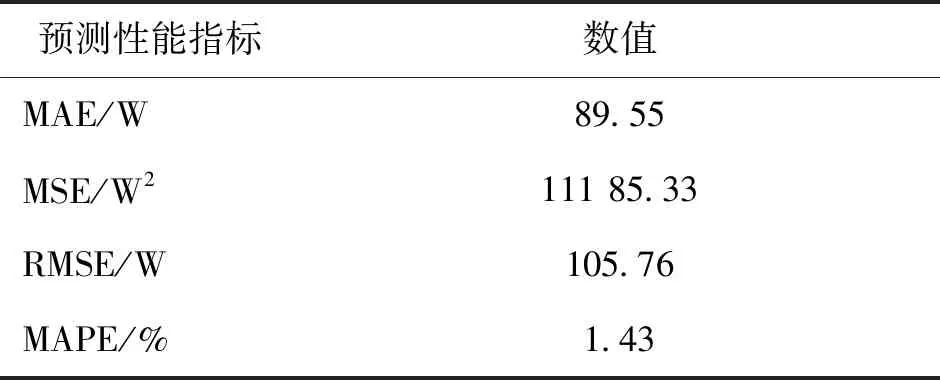
表2 测试集预测性能指标

由表2可知，相对百分误差MAPE=1.43%，表明SVR预测模型对多联机系统的能耗预测精度较高，MAE、MSE、RMSE数值均在正常范围内。图5所示为测试集预测绝对误差。结合表2中数据，SVR能耗预测模型预测稳定性良好，预测误差波动小，最大不超过400 W，集中分布在200 W以内。

3 PSO-SVR模型能耗预测结果及分析

3.1 PSO参数寻优结果

图3 多联机系统的结构

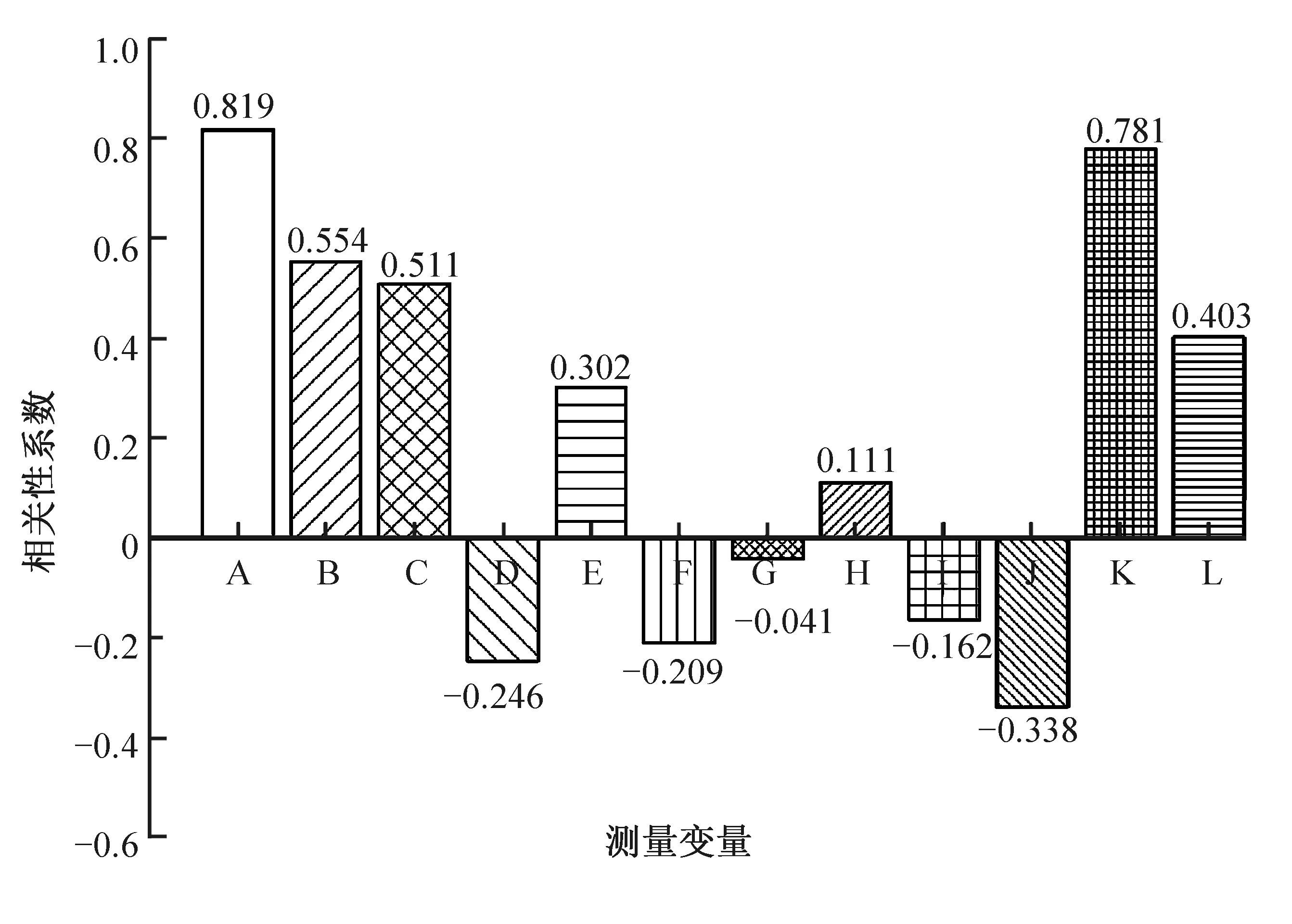
图4 相关性分析结果

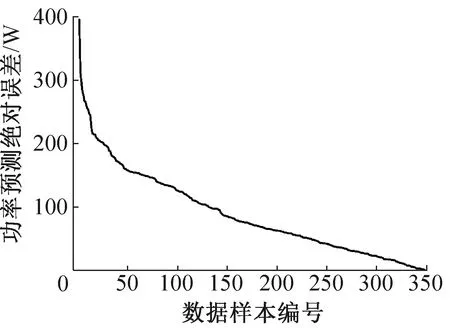
图5 SVR模型测试集预测绝对误差

设定粒子数目为20，迭代次数定为100次，学习因子根据文献推荐设定c1=c2=2，惯性权重初始取值为ω=1.2。用SVR模型5倍交叉验证的求得的平均MSE值作为目标适应度函数，对惩罚系数C和核参数γ进行参数寻优，并对粒子设置了自适应的变异因子以防止陷入局部最优化的求解循环，从而确保寻优结果的可靠性。

图6所示为PSO算法对多联机SVR预测模型参数寻优过程变化曲线。

图6 PSO算法对多联机SVR预测模型参数寻优过程变化曲线

由图6可知，群体最优适应度从迭代初始就得到了较好的寻优结果。PSO-SVR最终的参数寻优结果为C=10 000，γ=4.275。表3所示为参数寻优过程，模型参数优化问题在第7代就得到了全局最优解。

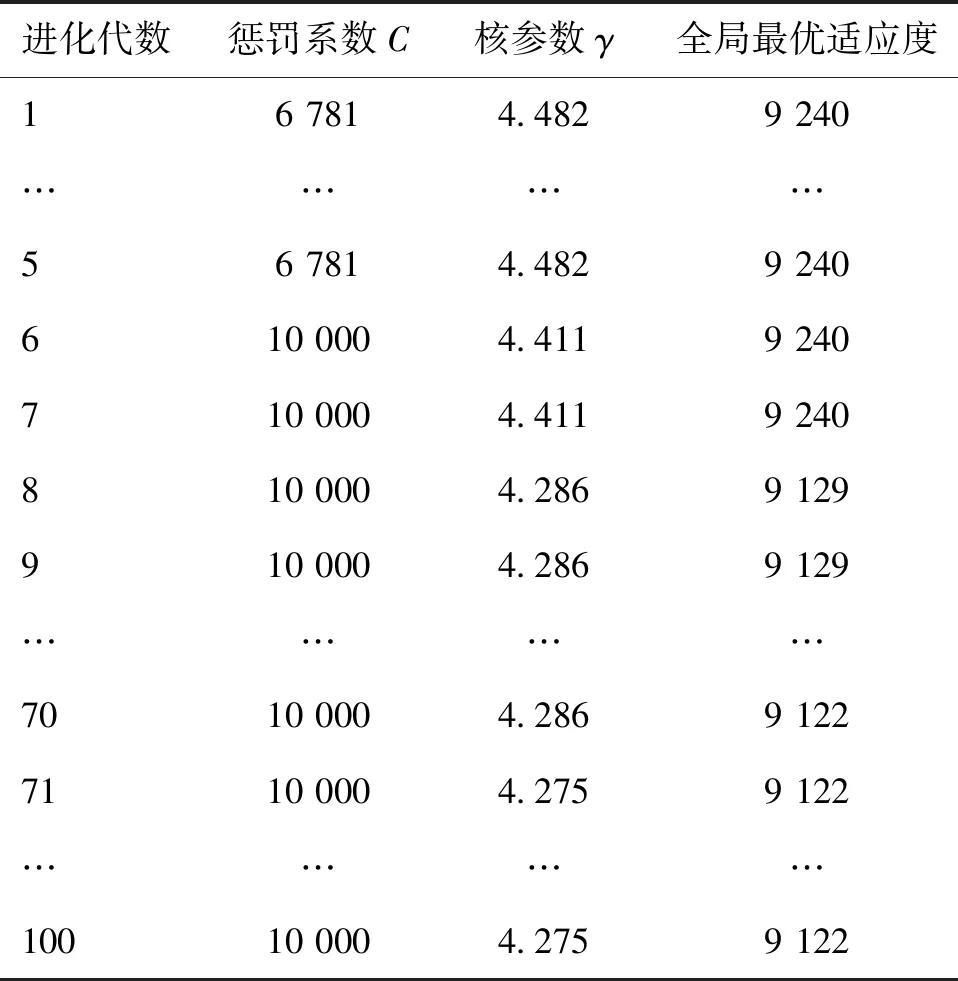
表3 参数C和γ优化过程记录

3.2 PSO-SVM模型预测结果

3.2.1 与SVR模型预测结果的对比

使用PSO算法寻优得到的参数结果重新设定SVR预测模型的惩罚系数C和核参数γ，测试集的预测结果如表4所示。各性能评价指标数值相较原始的SVR能耗预测模型，均有明显的下降，证明了PSO算法优化效果显著。

表4 使用PSO算法后测试集预测性能指标

图7所示为PSO-SVR模型测试集预测绝对误差。从预测绝对误差分布情况来看，整体预测绝对误差均控制在300 W以内，相比于图5中单一的SVR模型的测试集预测绝对误差分布情况，整体预测绝对误差波动范围大幅减小，多联机系统SVR能耗预测模型预测精度和稳定性均得到很好的优化。

图7 PSO-SVR模型测试集预测绝对误差

3.2.2 与经验公式计算结果进行对比

根据电压、电流、相位差、功率因数等参数，也可以通过理论公式计算得出多联机机组的实时功率。由于多联机机组部件较多，实验相关参数数目不足，因此无法通过电流、电压、相位差等参数来直接计算整个多联机组的功耗。为了对比理论公式计算法与PSO-SVR预测模型的优劣，在已有数据的基础上，通过制热量与功耗之间的关系来分析公式计算法的理论误差。

对于制热工况，制热量Qc可以由焓差法[16]按式(3)计算：

(3)

式中：qa为空气体积流量，m3/s；ha,i和ha,o分别为进、出口空气焓值，kJ/kg；va为湿空气的比容，m3/kg；da为空气的含湿量，g/(kg干空气)；Qlk为室内漏热量，W。

(4)

Y=1-0.548Δp/pB

(5)

ha=f(To,db,To,wb,pa,psp)=

(6)

Qlk=αlkAlk(Ti,db-To,db)

(7)

式中：Y为膨胀系数；pB为大气压，Pa；Δpn为喷嘴进出口两侧的压差，Pa；Cd为喷嘴的体积流量，m3/s；To,db,To,wb分别为干球温度和湿球温度，K；Xs=0.622pWS/(pB-pWS)为饱和空气含湿量，g/(kg干空气)，pWS为饱和蒸气压，Pa；αlk为漏热系数；Alk为漏热面积，m2；Ti,db为室内干球温度，K。

根据标准JJF 1059.1—2012[17]中的不确定度计算方法，对VRF制热能力的测量不确定度分析如式(8)所示：

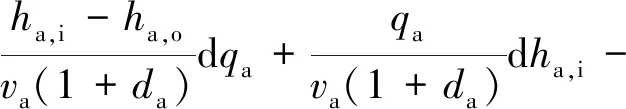
(8)

则可以按式(9)计算制热量的不确定度：

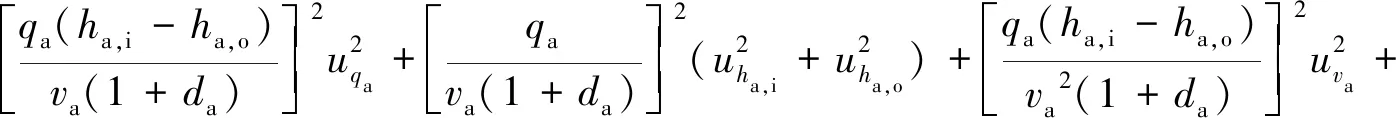
(9)

传感器的测量精度直接决定了不确定度的大小，表5中列出了各变量测量的不确定度。根据表中数据可以计算得出：c12uqa2=886.24，c22(uha,i2+uha,o2)=35 305.05，c32uva2=21.40，c42uda2=0.75，c52uQlk2=0.63。根据式(6)可以求得uQc=217.97 W。

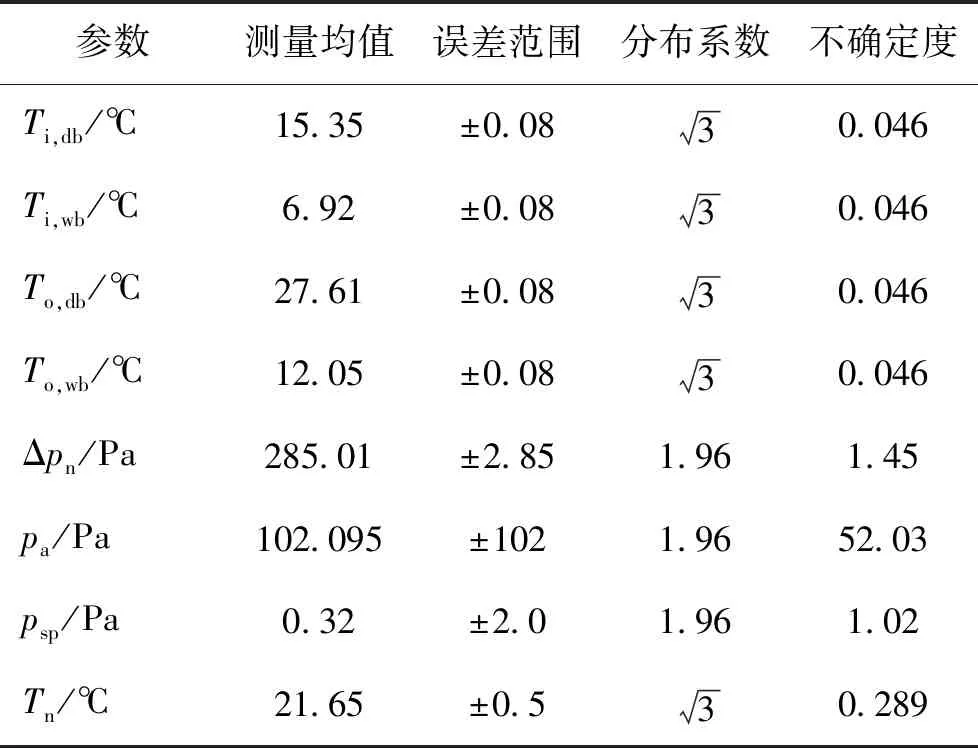
表5 各测量参数的测量不确定度

由能效比EER=Qc/WVRV，WVRV为多联机机组的功率， W。

机组功率的计算的不确定度uWVRV：

(10)

式中：Qm为制热量，W；EERm为能效比。

根据测量数据可得多联机机组功率的计算精度，各评估指标数值如表6所示。

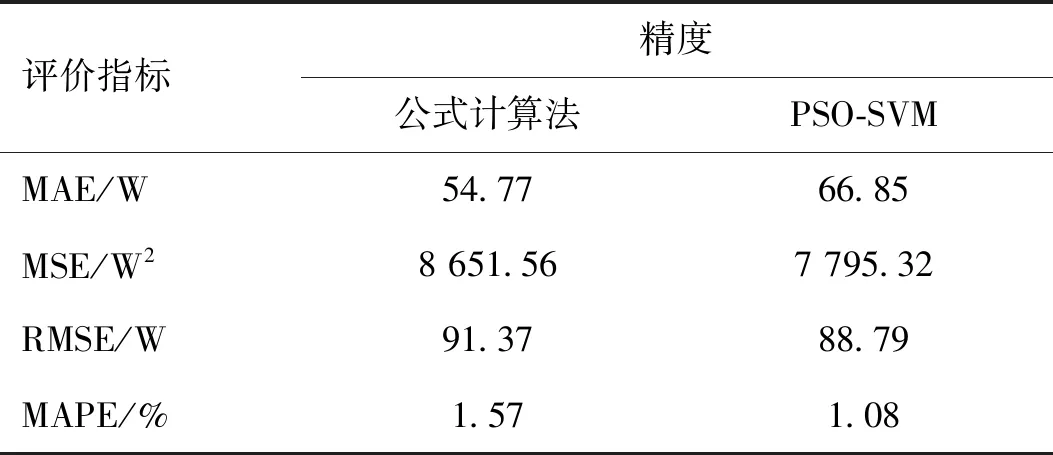
表6 公式计算法的精度

由表6可知，与理论公式计算法相比，PSO-SVR预测模型整体预测精度有大幅度下降，且预测精度的波动较小，预测稳定性更好。因此，运用PSO-SVR预测模型对多联机系统运行功率进行预测具有很好的适用性，相比于公式计算法，测量变量较少，测量系统更简单，经济性更好。

4 结论

本文将粒子群优化算法与支持向量回归方法相结合，建立了粒子群优化算法支持向量回归(PSO-SVR)预测模型，用于多联机的能耗预测，并通过与单一SVR模型预测结果进行对比，得出如下结论：

1)与单一SVR预测模型相比，PSO-SVR模型，MAE由89.55 W降至66.85 W，MAPE由1.43%降至1.08%，预测误差显著降低，预测精度更高。

2)与单一SVR预测模型相比，PSO-SVR模型的预测误差波动范围得到较好控制，RMSE由105.76 W降至88.79 W，保证了模型的稳定性。

3)相比于功率公式计算法，PSO-SVR预测模型整体预测误差有大幅下降，MAPE由1.57%降至1.08%，且预测误差波动较小，RMSE由91.37 W降至88.79 W，预测稳定性更好。

4)运用PSO-SVR预测模型对多联机系统运行功率进行预测具有很好的适用性，相比于公式计算法，仅需少量的测量变量，避免了测量系统的复杂性，经济性更好。

5)粒子群优化算法对多联机系统的SVR能耗预测模型性能改善效果显著，较大提升了能耗预测精度。