简化三方程转捩模型在高超声速流动中的应用

蔡林峰, 李昊歌, 赵文文, 陈伟芳

(浙江大学 航空航天学院, 浙江 杭州 310027)

0 引 言

对于高超声速飞行器而言，当流动发生转捩时飞行器表面热流和摩阻急剧增加。因此准确预估转捩起始点位置、转捩区长度，对于高超声速飞行器工程设计，尤其是热防护设计,具有重要意义，是目前航空航天工程中的关键问题。

采用转捩模型的RANS方法计算高效，是工程实践中开展流动转捩研究较为经济可行的技术手段，其中以Walters和Cokljat[1]、王亮和符松[2-3]以及Lantry和Menter[4]等人的研究最具代表性。Lantry等[4]提出的γ-Reθ t转捩模型完全基于当地化变量，能够和现代CFD程序相兼容，具备三维复杂外形转捩流动模拟能力，在工程中得到了广泛的应用。针对机翼、平板边界层流动的众多研究[4-6]表明，γ-Reθ t转捩模型能够准确捕捉各种类型的低流速边界层转捩，但对高超声速边界层流动转捩现象预测能力有限。为此，Kaynak等[7]基于来流马赫数对γ-Reθ t转捩模型经验关系式进行了可压缩修正，并针对超声速平板开展了数值验证工作。Gary等[8]对马赫数8尖锥进行了数值计算，研究了来流马赫数对γ-Reθ t模型中压力梯度参数的影响。国内孔维萱等[9]采用γ-Reθ t转捩模型对马赫数3～7范围内的高超声速尖锥流动进行了数值计算，验证了该模型具备高超声速边界层流动转捩模拟预测能力。张晓东等[10]给出了一种基于当地马赫数的γ-Reθ t转捩模型可压缩修正关系式，并在高超声速双楔和平板算例中的得到了验证。张毅峰等[11]通过压力梯度参数和普朗特数对γ-Reθ t转捩模型进行了修正，并在多个高超声速尖锥转捩流动的模拟中都得到了不错的结果。郑赟等[12]参考高超声速风洞实验数据对γ-Reθ t转捩模型提出了改进，通过数值计算分析了原始γ-Reθ t转捩模型对高超声速边界层转捩流动预测结果与实验值不吻合的原因。周玲等[13]则在符松和王亮[2-3]提出的转捩模式上进行了壁面温度影响修正，并针对高超声速飞行器前体边界层强制转捩开展了数值研究。

本文作者所在课题组[14]在γ-Reθ t转捩模型的基础上，通过去掉转捩动量厚度雷诺数输运方程，提出了简化三方程转捩模型。该模型经验关系式简单，对低速机翼、高超声速平板等边界层流动有良好的模拟预测能力。但在对高超声速双楔模型的数值模拟中发现，壁面热流计算结果与实验值存在一定差距。因此，本文将在该模型的基础上引入湍流模型和转捩模型的可压缩修正方法，研究可压缩修正对简化三方程转捩模型预测高超声速流动转捩的影响，为该模型的进一步改进提供参考。

1 数值计算方法

1.1 控制方程

控制方程由三维可压缩Navier-Stokes方程、k-ωSST湍流模型方程和间歇因子输运方程组成。方程基于结构网格有限体积方法求解，时间离散采用计算效率更高的LU-SGS隐式方法，空间对流通量采用AUSMPW+格式结合MUSCL差值方法进行求解。

1.2 简化三方程转捩模型

在原始γ-Reθ t转捩模型中，动量厚度雷诺数输运方程的作用是将边界层外的信息传播至边界层内，并将转捩判据、经验关系式和间歇因子联系起来。Coder和Maughmer[15]的研究表明，通过定义一个当地化的压力梯度参数Hc=yΩ/U来构造新的经验关系式，可以去掉转捩动量厚度雷诺数输运方程并取得较为合理的模拟结果。类似的，定义参数Tw=RTΩ/ω于表征剪切力和压力梯度大小，从而构建一个新的临界动量厚度雷诺数经验关系式：

Reθ c=900.0-810.0×

(1)

同时，定义转捩区域控制函数为：

Flength=max(0.1,30.0lnTu∞+89.97)

(2)

式(1)和式(2)中系数由平板转捩流动拟合得到。综上，耦合间歇因子γ的输运方程和k-ωSST湍流模型方程可得完整的简化三方程转捩模型为：

(3)

上式中Pγ和Eγ分别表示间歇因子输运方程的生成项和破坏项，其具体形式有：

Pγ=Flengthca1ρS(γFonset)0.5(1-ce1γ)

(4)

Eγ=ca2γρΩFturb(1-ce2γ)

(5)

最终通过间歇因子γ修正湍动能输运方程来耦合简化转捩模型与k-ωSST湍流模型，可得修正后的湍动能输运方程生成项和破坏项分别为：

(6)

(7)

为有效模拟流动分离，间歇因子γ的修正公式如下：

Freattach,2)Fθ t

γeff=max(γ,γsep)

(8)

相比于原始的γ-Reθ t转捩模型，简化三方程转捩模型(算例中用k-ω-γ表示)减少了一个输运方程，且经验关系式更为简单，无需迭代求解。后续将对该模型进行可压缩修正，进而开展高超声速转捩流动的数值研究。

2 压缩性修正

2.1 湍流模型压缩性修正

针对高超声速湍流流动，国内外学者提出了多种不同形式的k-ωSST湍流模型可压缩修正方法(算例中湍流模型可压缩修正用TUCC表示)。本文将采用Wilcox等人[16]提出的可压缩修正方法对湍流模型进行修正，从而提高k-ωSST湍流模型对高超声速湍流流动的模拟能力。修正形式如下：

β*=β*[1+ξ*F(Mt)]

(9)

β=β-β*ξ*F(Mt)

(10)

其中：

ξ*=2.0,Mt0=0.25

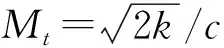
2.2 简化转捩模型压缩性修正

简化转捩模型的临界动量厚度雷诺数经验公式是根据平板实验数据拟合得到的，在应用于高超声速可压缩流转捩问题时需要进行适当的可压缩修正。因此，文献[10] 给出了一种基于来流马赫数的可压缩修正方法(算例中记为TRCC)。该方法定义了一个来流马赫数函数来对临界动量厚度雷诺数进行修正，具体修正形式如下：

F(Ma∞)=(1+0.38)0.5

(11)

3 数值计算结果与分析

3.1 高超声速平板流动

算例取自文献[17]，高超声速平板长1.5 m，计算来流条件见表1。计算网格224×150，壁面第一层网格y+小于1。

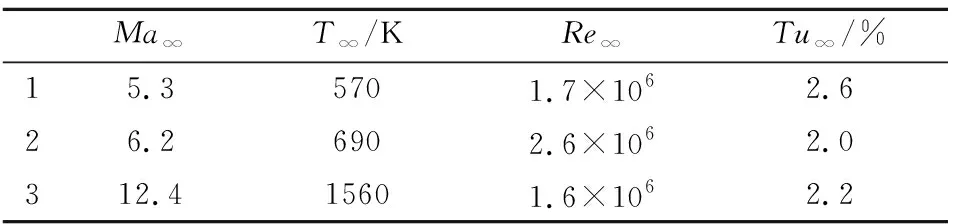
表1 来流条件

图1至图3分别给出了三种不同计算来流条件下高超声速平板壁面斯坦顿数分布。可以看到，完全层流和完全湍流模型计算结果与实验值相差较大，无法捕捉流动转捩现象。增加简化三方程转捩模型后，计算结果能够实现层流到湍流的转捩过渡，并且转捩起始位置、转捩区长度、转捩前后平板壁面斯坦顿数都能够与实验数据以及文献[18]中的计算结果相吻合。可见简化三方程转捩模型对于简单平板高超声速转捩流动具有不错的模拟能力。此外，从图1至图3中可以看到，添加可压缩修正后，虽然对高超声速平板转捩位置等无明显影响，但壁面斯坦顿数在转捩后湍流区域有所下降，相比实验结果偏低，后文将通过复杂几何模型转捩流动的数值计算对该模型及其可压缩修正在高超声速转捩流动中的应用开展进一步的研究。

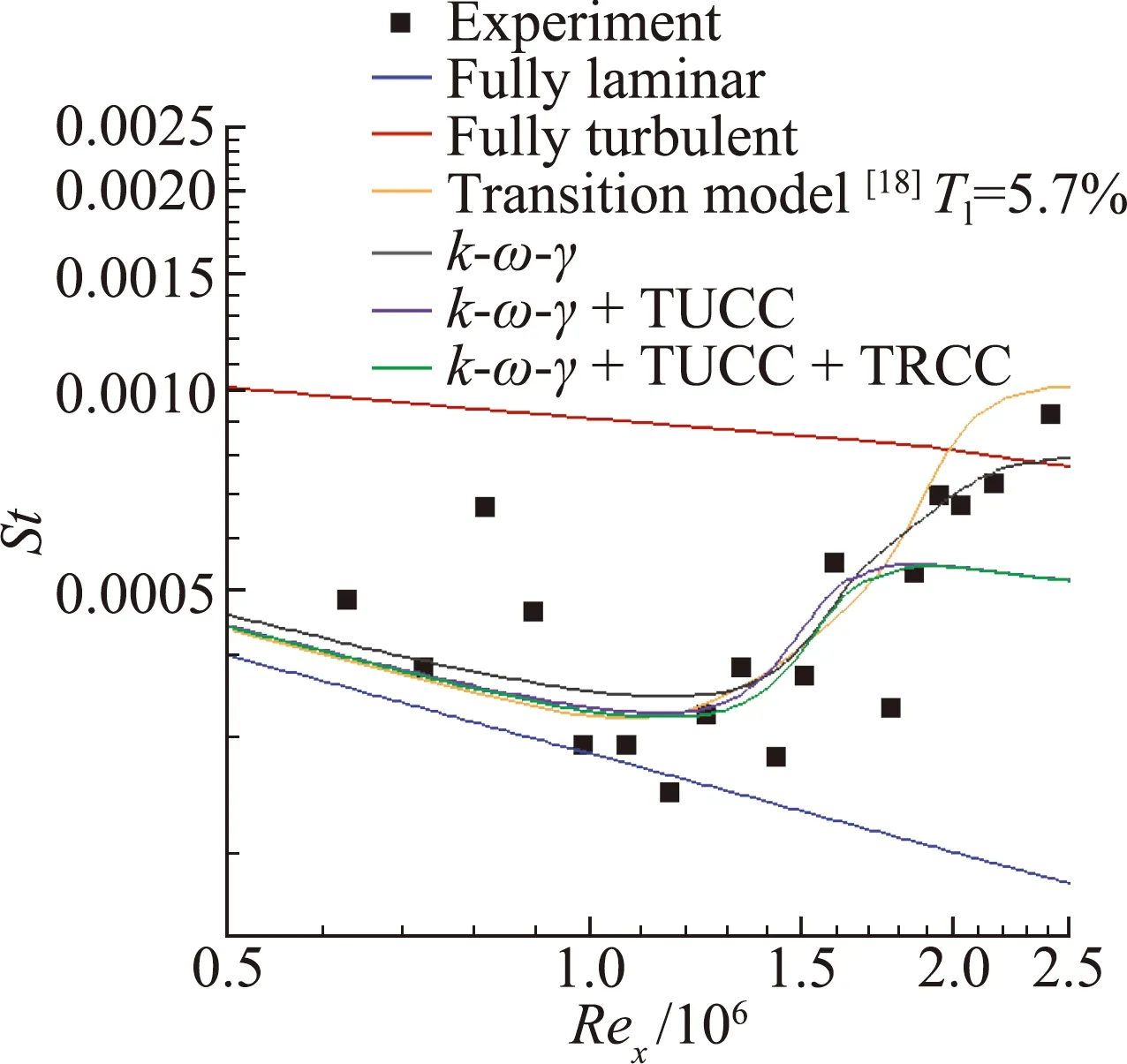
图1 计算条件1时的高超声速平板壁面斯坦顿数分布图

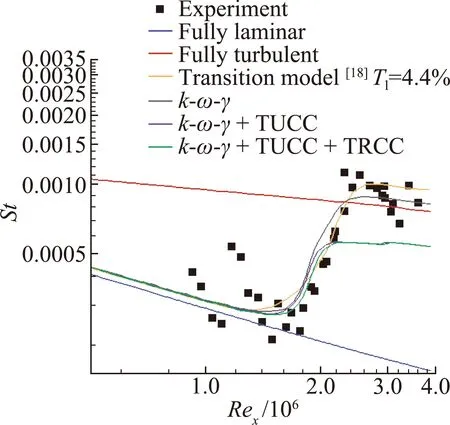
图2 计算条件2时的高超声速平板壁面斯坦顿数分布图

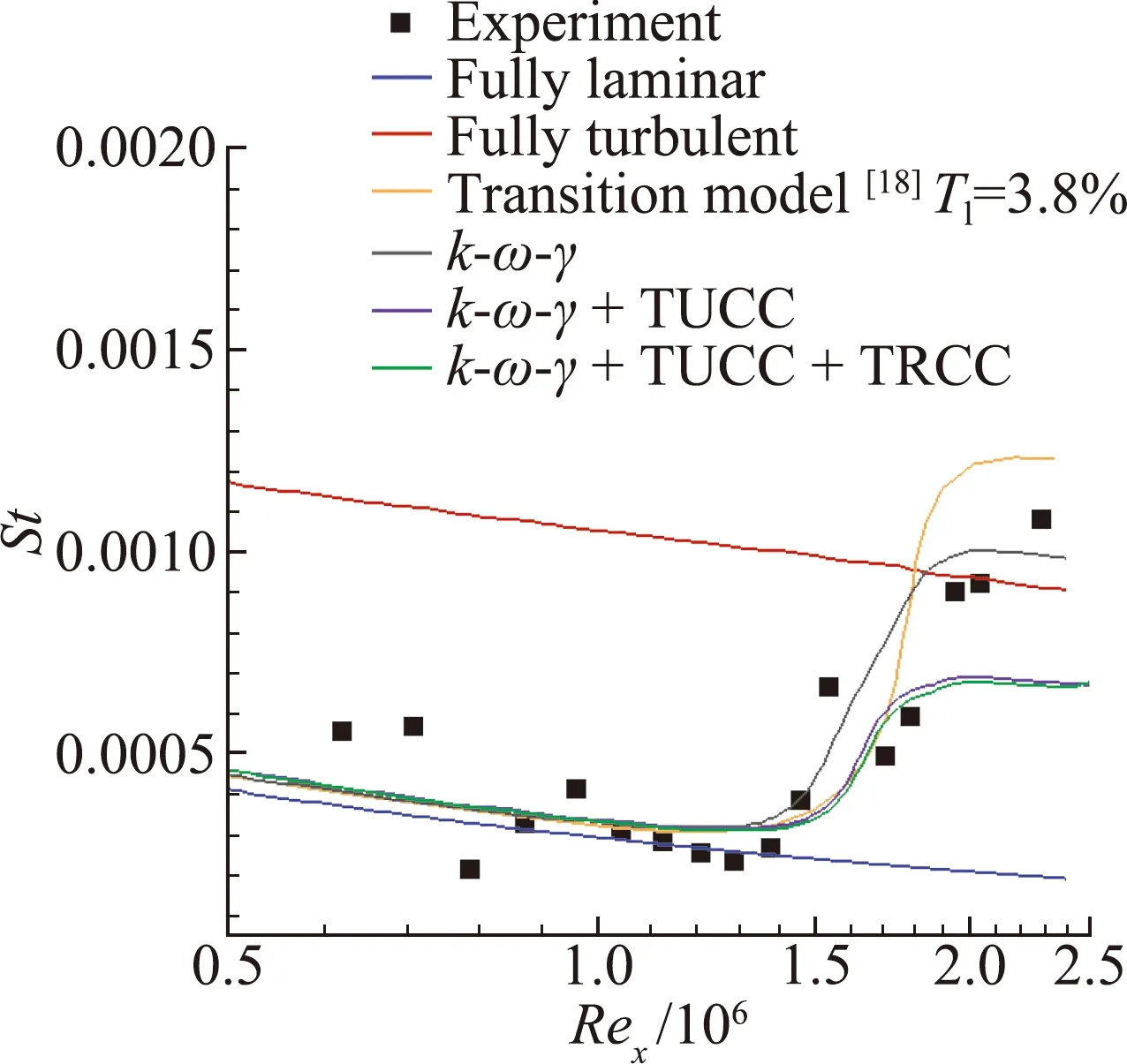
图3 计算条件3时的高超声速平板壁面斯坦顿数分布图

3.2 高超声速双楔流动

双楔模型外形如图4所示，前缘钝化半径0.5 mm，其中两个坡的角度分别为9°和20.5°。来流马赫数为8.1，静压为520 Pa，静温为106 K，来流单位雷诺数为3.8×106/m，来流湍流度0.9%，壁面温度为300 K。计算网格见图5，壁面第一层网格y+小于1。

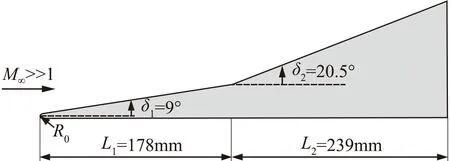
图4 双楔模型几何外形

图5 双楔模型计算网格示意图

图6是采用原始简化三方程转捩模型计算得到的流场马赫数云图，流场结构与实验结果基本一致。拐角处可以看到明显的流动分离和再附，分离激波和再附激波在拐角后交汇，之后再与头部诱导的弓形脱体激波相交。

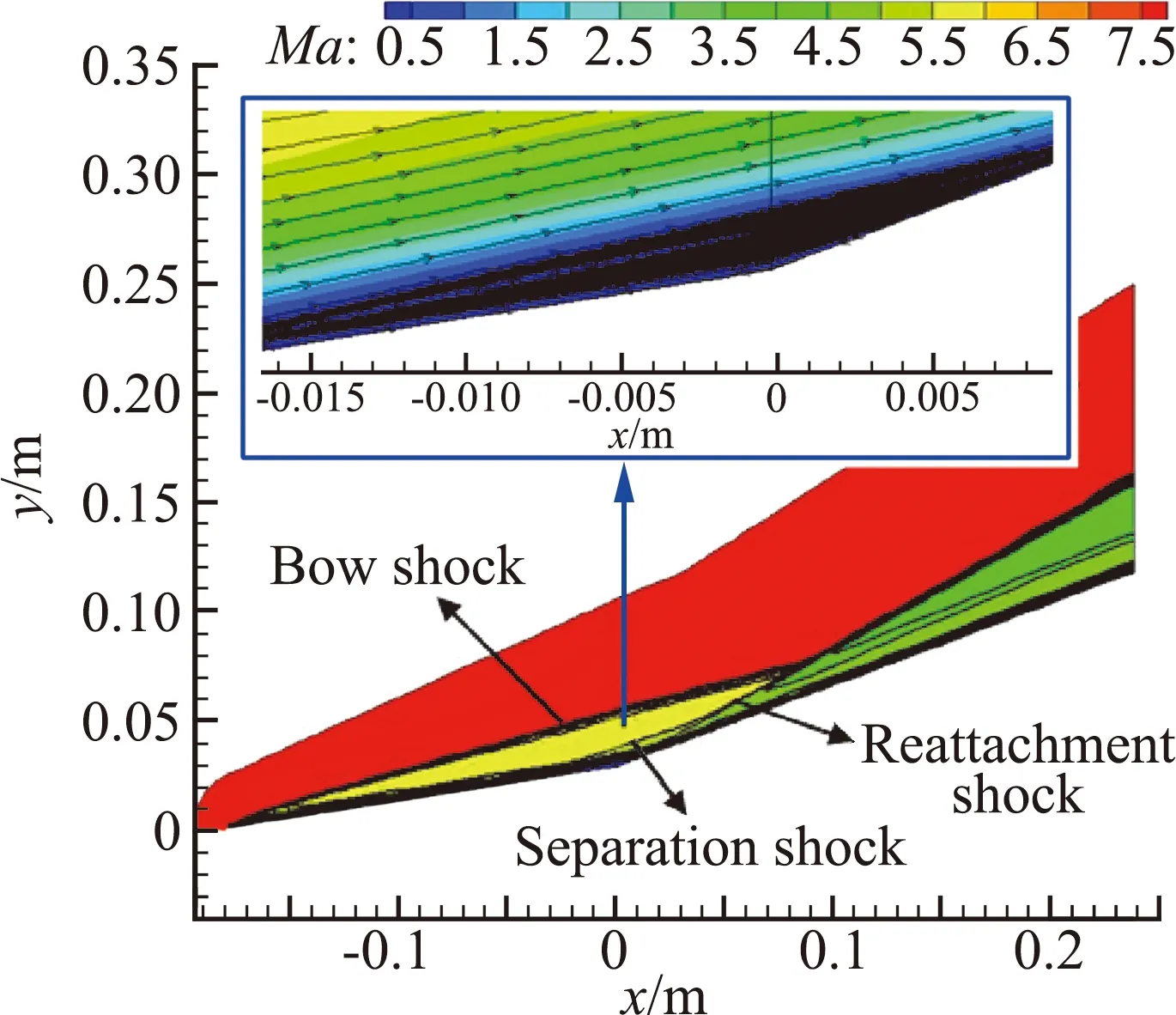
图6 双楔模型马赫数分布云图

双楔模型壁面斯坦顿数、压力系数分布图见图7和图8。从图中可以看出简化三方程转捩模型相比完全层流模型和完全湍流模型,计算结果与实验值更为接近。且从计算结果可以看出，在拐角处流动分离转捩为湍流，壁面斯坦顿数明显增大，说明流动转捩为湍流后壁面热流急剧增大。但是，对比实验结果也可以看到,流动发生转捩后，原始简化三方程转捩模型计算得到的壁面斯坦顿数相比实验值明显偏高，与实验值存在一定误差。对比图7中添加湍流模型可压缩修正后的结果可以看到，流动转捩后壁面斯坦顿数计算结果相比实验值偏高，主要是由于原始的k-ωSST两方程湍流模型不适用于高超声速湍流流动造成的。对k-ωSST两方程湍流模型增加可压缩修正后湍流区热流计算结果得到了明显改进。但图8中湍流模型可压缩修正添加前后压力系数分布曲线无明显变化，可以看出，湍流模型可压缩修正对壁面压力系数分布无影响。可见，湍流模型的可压缩修正方法能够有效降低双楔模型湍流区壁面热流的模拟结果，使之与实验结果更为吻合。相应的，添加简化转捩模型可压缩修正后，模型能够更好地描述流动的压缩性，计算得到的转捩区域增大，双楔模型壁面斯坦顿数、压力系数与实验值更为吻合，具有不错的修正效果。

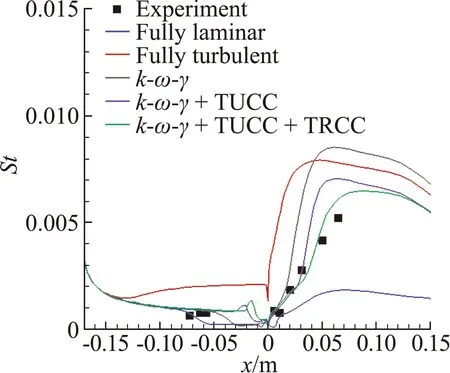
图7 双楔模型壁面斯坦顿数分布图

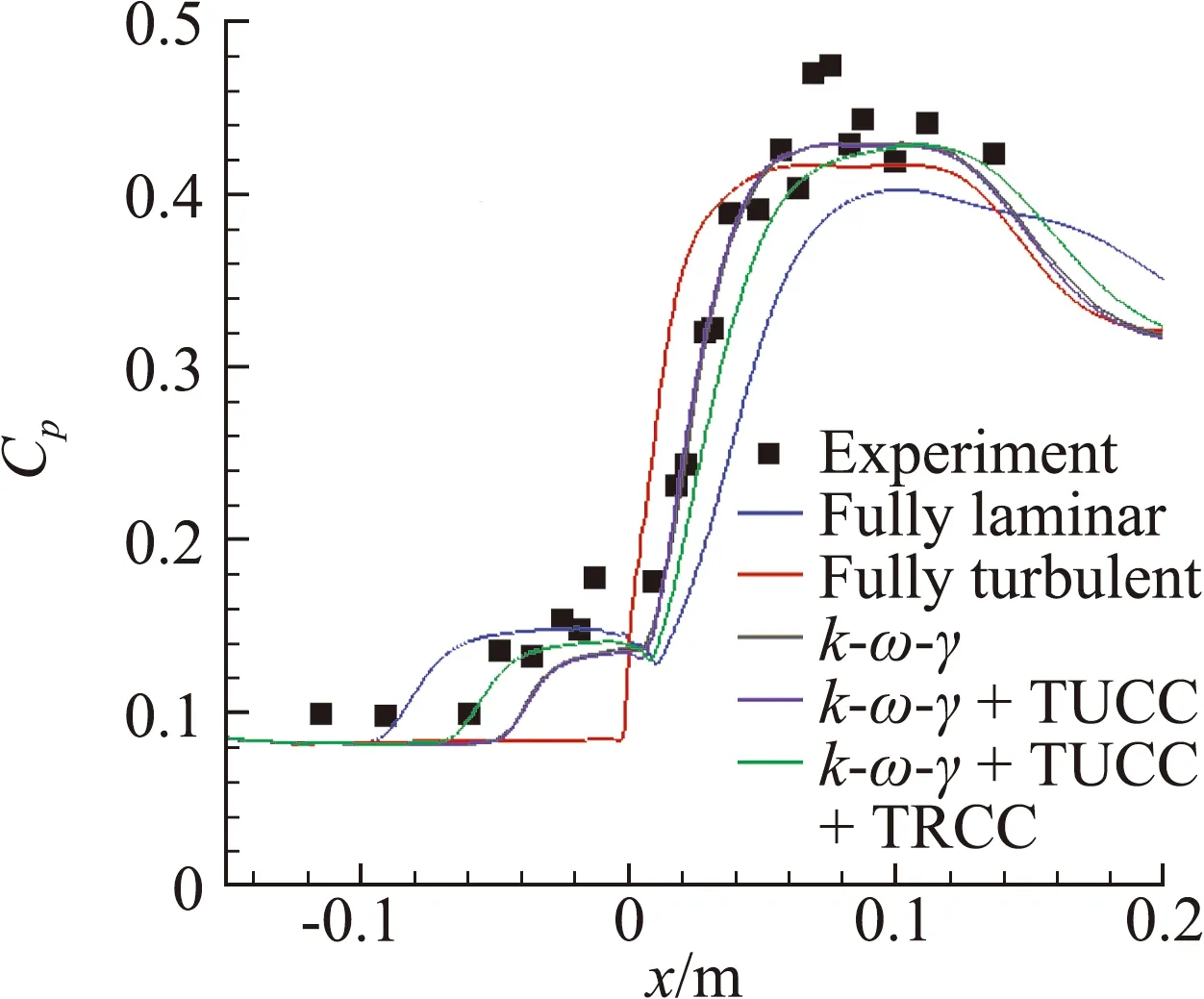
图8 双楔模型壁面压力系数分布图

3.3 高超声速尖锥流动

高超声速尖锥算例取自文献[19]。如图9所示，尖锥长2.35 m，半锥角为7°。计算来流马赫数7.15，静压7722 Pa，静温214 K，来流单位雷诺数9.64×106/m，湍流度0.06%，壁面温度300 K。采用半模计算以减少网格量，尖锥对称面上网格如图10所示，其中壁面第一层网格间距为1×10-6m。

图9 尖锥外形

图10 尖锥对称面网格示意图

由图11可以看到，相比于全层流模型和全湍流模型，简化三方程转捩模型能够准确捕捉流动转捩现象，在0.67 m位置处流动发生转捩，与实验结果相吻合。此外，从图11中可以看到湍流模型和转捩模型的可压缩修正对转捩位置没有影响。其中湍流模型可压缩修正主要用于确保k-ωSST湍流模型对高超声速湍流流动模拟的准确性，降低了流区的热流计算值。而转捩模型可压缩修正主要用于确保对转捩区流动压缩性的准确描述，从而保证转捩区长度的准确计算，最终复现了实验结果。

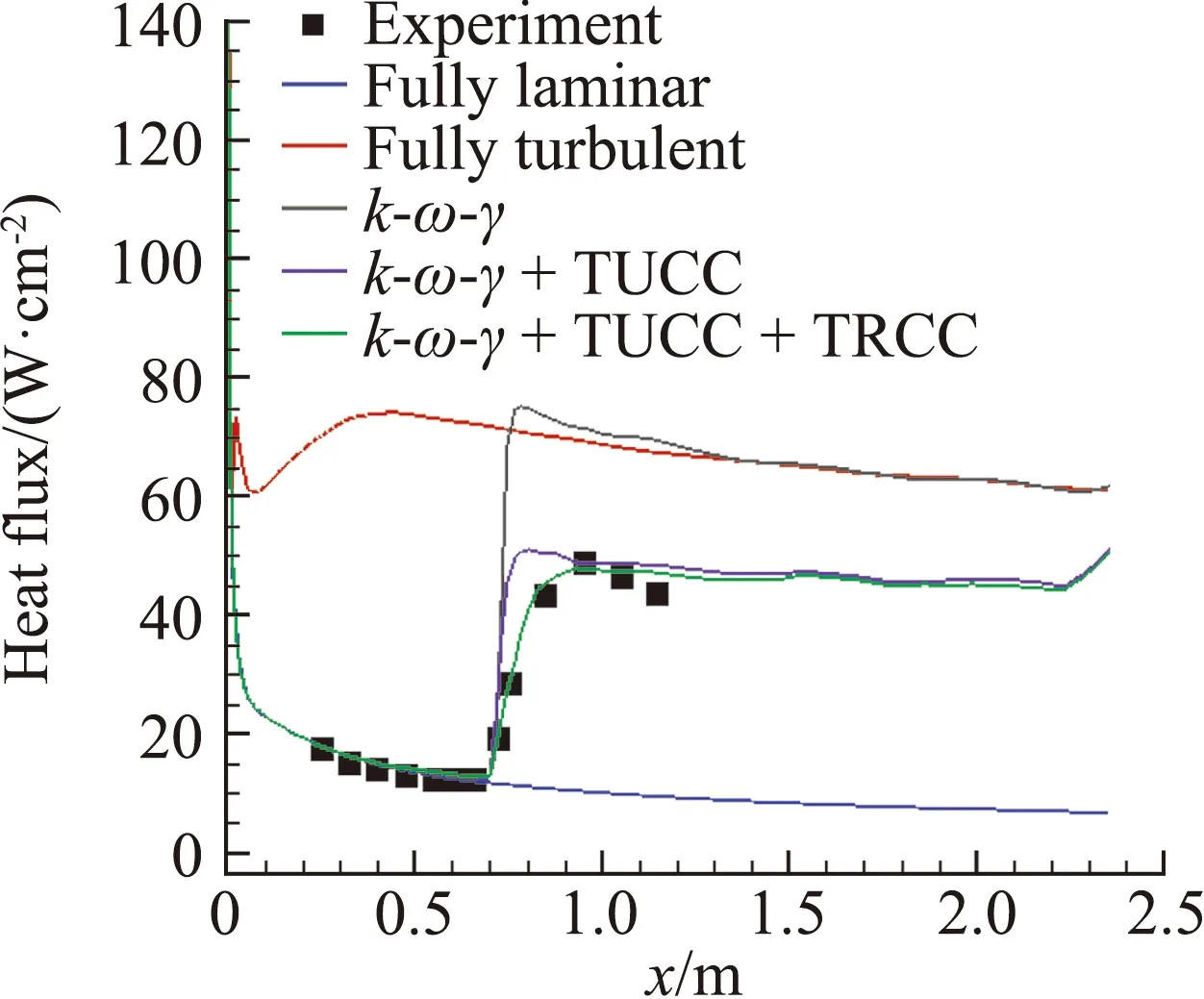
图11 尖锥壁面热流分布

4 结 论

通过对湍流模型和简化转捩模型进行可压缩修正，研究了简化三方程转捩模型在高超声速转捩流动中的应用。对比高超声速平板、双楔、尖锥的数值计算与实验结果，得出以下结论：

1)简化三方程转捩模型对于高超声速转捩流动具有模拟预测能力，能够较好地复现流场结构，准确捕捉转捩起始位置，但对壁面热流和转捩区长度的模拟结果与实验数据存在差距，需要引入合适的可压缩修正方法来提高模型计算精度。

2)湍流模型可压缩修正方法主要用于修正湍流区的壁面热流模拟结果，而简化转捩模型临界动量厚度雷诺数经验关系式对转捩区长度影响较大，添加可压缩修正能够改进模型对高超声速流动转捩的模拟能力。

3)简化三方程转捩模型经验关系式由平板转捩数据拟合得到，对于双楔、尖锥模型需要添加修正后才能够更为准确地预测壁面热流、转捩区长度。计算结果与计算外形相关，发展更具普适性的高超速边界层转捩预测方法仍然需要更深入的探索研究。