2种壁厚偏差模型的管材液压成形厚度分布研究

刘 琴， 杨连发， 郭 建， 何玉林

(桂林电子科技大学 机电工程学院，广西 桂林 541004)

利用液压胀管技术，能够将管材胀形成具有复杂曲面形状且强度性能更好的产品，同时能使材料的利用率更高、成本更低，符合环保节能需求[1]。在管材液压胀形中，将薄壁管的壁厚假设为均匀的情况下，直管的自由胀形看作具有旋转对称性的形状，但是在实际的工业生产中，管材加工的过程会产生表面缺陷和尺寸精度、管材机械性能不高等缺陷[2]，导致金属管的管壁厚度并不总是均匀的。在利用金属管材进行液压成形，需要较高的尺寸形状精度的成形件时就必须考虑管材的壁厚不均匀。

不少学者为提高管材成形后壁厚的均匀性做了不少的研究。Yang等[3]在分析脉动液压的管材自由胀形时发现，经脉动加载路径诱导的组织演变有助于提高管材的形状精度和壁厚均匀。吴量等[4]研究发现，成形模具对管材的摩擦系数越小，胀形后的最大减薄量越小。崔亚平等[5]在研究大减径比阶梯管坯的液压胀形时发现，增加轴向力可使材料的流动性和补料效果更好，使得管材胀形后的截面壁厚均匀性增加。也有不少学者根据实际管材存在的壁厚偏差对管材胀形进行了研究。Kuwabara等[6]发现初始厚度的均匀性取决于制造工艺，厚度越均匀，管材的成形性越高。Fuchizawa等[7]在研究初始偏心距管材、初始厚度偏差为1%～4%时，认为胀形过程中厚度偏差的增加取决于初始壁厚偏差的程度。文献[8-9]研究管材的初始壁厚偏差对自由胀形的影响发现，自由胀形过程中壁厚偏差的增加与管材材料和管端边界条件有关。He Zhubin等[10]研究了具有不同初始偏心距的薄壁管的液压胀形发现，薄壁管的变形行为和成形极限与偏心距有很大关系，偏心距越大，变形截面的椭圆度越大。王海艳等[11]对厚度为1 mm的消音管进行模拟和实验对比发现，消音管胀形后壁厚相对偏差小于3%，且相对变化趋势一致，说明模拟软件能够较好地反映管材胀形后的壁厚分布。

鉴于此，针对实际的管材壁厚分布，提出2种壁厚偏差模型，探讨2种壁厚模型胀形后的优缺点，为管材液压成形的成形件得到更好的壁厚均匀性提供技术支撑。

1 模型和模拟参数的设置

1.1 模型的提出

对于标准外径为25 mm，标称壁厚为0.6 mm的管材，测量得到管材壁厚偏差率为8.9%～11.9%，最大壁厚为0.66 mm，最小壁厚为0.59 mm。对长度为110 mm、中截面(管材长度为55 mm处)的初始壁厚偏差率为9.3%的管材进行液压自由胀形，对管材初始最厚处与最薄处做好标记，胀形后管材如图1所示。利用DIC技术可以得到管材最大胀形高度hmax为17.83 mm，最小胀形高度hmin为16.54 mm，最大胀形高度发生在壁厚最薄处，说明壁厚的分布与管材的成形极限和胀形后的形状均匀性有很大的关系。

图1 管材自由胀形图

根据壁厚分布比较偏心距、椭圆2种壁厚偏差模型，设置2种模型的壁厚偏差率都为10%。偏心距模型的偏心距为0.03 mm，最大壁厚和最小壁厚分别为0.66 mm和0.60 mm，如图2(a)；椭圆模型的圆心与外径圆的圆心重合，如图2(b)。为了保证2种模型的壁厚偏差率一致，椭圆模型的最大壁厚和最小壁厚与偏心距模型相同。管材的壁厚偏差率定义为：

其中：tmax是管材周向最大壁厚；tmin是管材周向最小壁厚。

图2 2种壁厚偏差模型

1.2 模拟的简化与设置

依据实际的液压成形实验，在对液压成形不失真和计算结果的准确性影响不大的前提下对有限元模拟模型进行简化：1)假设密封柱和模具为刚体，忽略在胀形过程中的弹性变形；2)因为液压成形是冷变形，所以不考虑在胀形过程中由摩擦和变形等引起的温度变化。通过ABAQUS有限元软件对管材液压胀形过程进行模拟。有限元数值模拟模型中,主要包括密封柱、模具和管材，密封柱和模具均视为恒温刚性体，管件设置为变形体。

无缝钢管作为液压胀形的模拟管材，管材密封柱的形状与管材内径一致，管材长度110 mm，密封柱和模具的长度为30 mm，胀形区长度为50 mm，其中模具的内径设置为12.5 mm，外径为15 mm。密封柱和模具与管材的接触设置为面与面接触，摩擦系数统一设置为0.15，建立模型并且划分网格。模型中选用六面体网格，管材的网格尺寸为0.4 mm。由于密封柱和模具为刚体，不参与模拟的计算，密封柱和模具的网格尺寸根据系统默认设置为3.4 mm和4.2 mm。2种模型的内径不同，所以两者的密封柱模型不同，2种模型的密封柱网格个数也不一样，2种模型的网格数量如表1。

有限元模拟装置模型如图3所示。坐标系定义为：X轴和Y轴为管件的径向，Z轴为管的轴向，坐标原点为管件左端面圆心。管材端部在胀形过程中

表1 有限元模型各部件网格数量

图3 有限元模拟装置模型

受到模具的径向约束，中间部分不受模具约束，在液压力作用下产生自由变形。密封柱和模具设置为X、Y、Z方向不发生位移，且不发生旋转。设置管材的X、Y、Z方向位移不受约束。

2 有限元模拟结果与分析

管材在液压力作用下的自由胀形过程中，成形主要由管材壁厚的变薄和轴向的自然收缩来完成。图4(a)为偏心距模型的胀形结果图，图4(b)为椭圆模型的胀形结果图。

图4 2种模型的胀形结果图

由于未在有限元模拟软件中设置管材胀形破裂条件，在模拟软件ABAQUS的场输出胀形时液压力增加到35 MPa，模拟的胀形高度与实验的实际管材胀破时高度接近，取此时的场输出数据进行分析。表2为在液压力达到35 MPa时，取2种模型外径的中心原点为基准，得到2种模型的胀形高度。在相同的液压力作用下，偏心距模型的胀形高度略低于椭圆模型，但偏心距模型的形状偏差率大于椭圆模型，椭圆模型胀形后的形状更均匀。这是因为偏心距模型壁厚超过基准厚度0.6 mm部分大于椭圆模型，薄处的材料流动性更好。径向最大位移发生在初始壁厚最薄的部位，从最薄部位过渡到最大壁厚部位，径向位移逐渐减小，这与实际的试验结果相符。

表2 2种模型的胀形高度和形状偏差率

2种模型胀形后壁厚分布如图5所示。从图5可看出，偏心距模型的最小壁厚为0.440 mm，椭圆模型的最小壁厚为0.433 mm。根据材料的体积不变原则，椭圆模型的最小壁厚小于偏心距模型，其胀形区最大高度高于偏心距模型。胀形后的偏心距模型最大壁厚为0.543 mm，椭圆模型的最大壁厚为0.513 mm，虽然2种模型初始最大壁厚相同，但在胀形后的壁厚偏差率(18.5%)比偏心距模型的壁厚偏差率(23.4%)更低。偏心距模型的周向最薄处减薄了0.160 mm，最厚处减薄0.117 mm；椭圆模型的周向最薄处减薄了0.167 mm，最厚处减薄了0.147 mm。椭圆模型的最厚位置与最薄位置相差90°，偏心距模型的最厚位置与最薄位置相差了180°，椭圆模型的材料流动性更高。

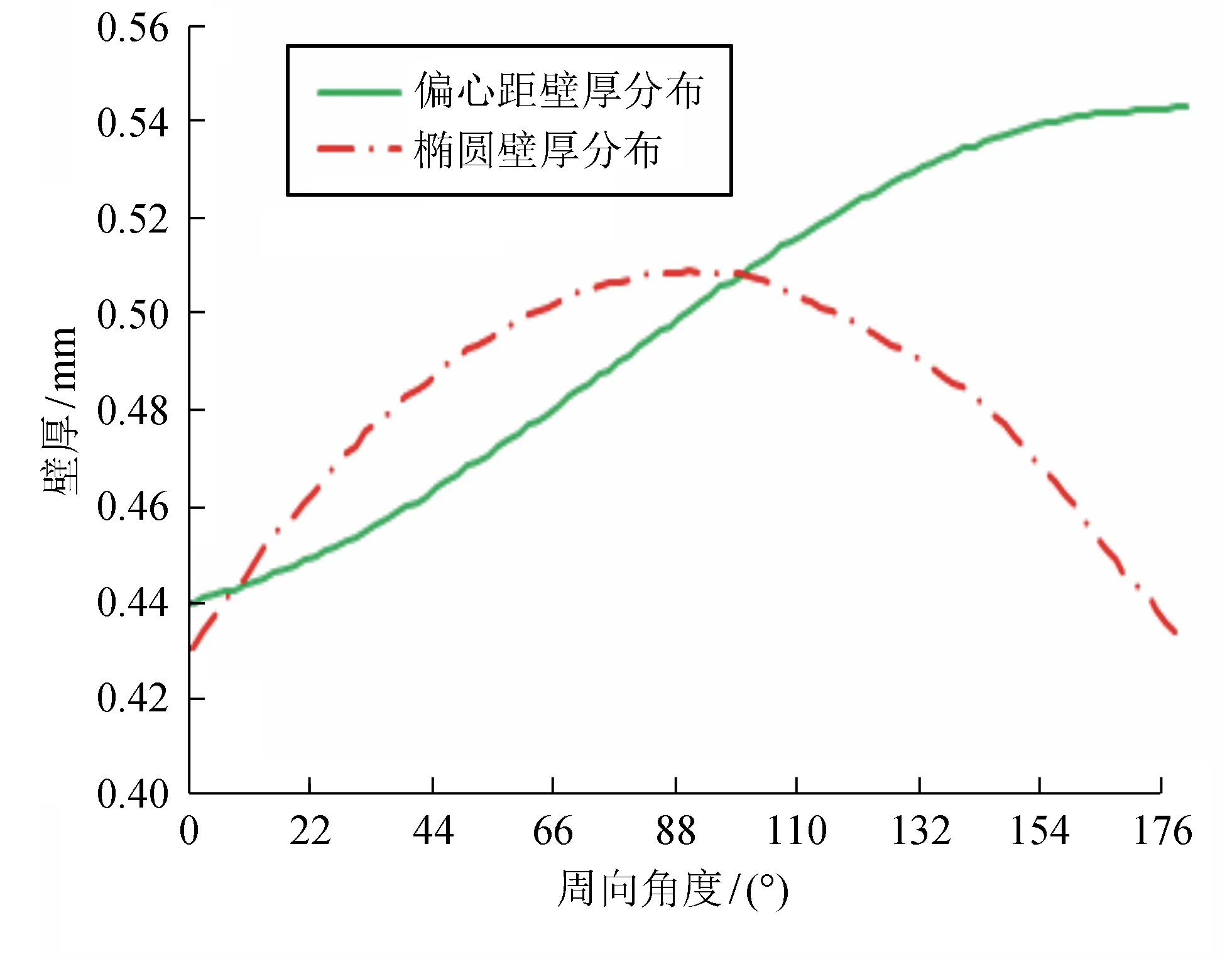
图5 2种模型胀形后壁厚分布

3 结束语

通过ABAQUS模拟软件，对2个初始壁厚偏差率相同、壁厚分布不同的管材进行有限元模拟，对模拟结果比较分析，得出如下结论：

1)在相同的初始壁厚偏差率下，随着胀形的进行，2种模型的壁厚偏差率都在不断增加，但偏心距模型胀形后的壁厚偏差率比椭圆模型大。

2)在胀形的过程中，由于2种模型初始壁厚分布的差异，径向最大胀形高度在管材周向最薄处，这与实际的试验结果相符。说明在薄处的材料流动性更好，椭圆模型的管材材料流动性比偏心距模型更高。

3)在相同的壁厚偏差率下管材液压胀形，椭圆模型能在周向得到更均匀的壁厚分布和更低的形状偏差，所以在实际生产中，要想得到胀形后尺寸精度更高的胀形件，在相同的壁厚偏差下，应选择椭圆模型的管材。