基于 Q 学习算法的高速铁路列车 节能优化研究

张 淼，张 琦，张梓轩

ZHANG Miao1，2，3，ZHANG Qi2，3，ZHANG Zixuan4

（1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 通信信号研究所，北京 100081；3.中国铁道科学研究院集团有限公司 国家铁路智能运输系统工程技术研究中心，北京 100081；4.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

(1.Postgraduate Department， China Academy of Railway Sciences， Beijing 100081， China；2.Signal and Communication Research Institute， China Academy of Railway Sciences Corporation Limited， Beijing 100081， China；3.National Research Center of Railway Intelligence Transportation System Engineering Technology， China Academy of Railway Sciences Corporation Limited， Beijing 100081， China；4.State Key Laboratory of Traffic Control and Safety， Beijing Jiaotong University， Beijing 100044， China)

0 引言

近年来，随着人民对运输速度及服务质量需求的不断提高，我国高速铁路运行里程得到飞速增长。截至2018年底，我国高速铁路运营里程达2.9万km，超过世界高速铁路总里程的65%。高速列车的运行速度和运行距离的增长伴随着巨大的能源消耗，高速铁路系统能耗总量的不断上涨及对高效环保和可持续发展的倡导，使高速铁路节能方法和技术研究十分关键。据统计，整个高速铁路能耗的80%均来自牵引能耗[1-2]。高速列车在规定的时间内有多种不同的驾驶策略到达目的地，站间不同驾驶策略的运行能耗图如图1所示。高速列车节能驾驶策略是在保证列车准点、安全的前提下，寻求一条牵引能耗最小的运行曲线。列车最优节能驾驶策略实质上是一类最优控制问题，列车的牵引力和制动力是优化控制的输入变量，列车速度和位移是列车状态变量。约束条件是站间运行时分，线路限速、变坡道、牵引力和制动力限制等，优化目标是最小化运行过程中的牵引能耗，最终目的是求得列车在站间的最优驾驶序列及相应的转换点。

图1 站间不同驾驶策略的运行能耗图Fig.1 Energy consumption diagram of different driving strategies between stations

近些年，国内外的学者们运用多种方法对列车运行能耗的优化问题进行研究，王轶[3]引入迭代学习控制理论，对高速列车的基本阻力公式(Davis公式)的参数进行辨识。衷路生等[4-6]基于高速列车单质点力学行为的随机离散非线性状态空间模型，从概率的角度解决了模型中存在不完全可测列车状态的困难，同时应用子空间建模方法提出了高速列车的子空间预报模型，并针对高速列车过程模型存在时变参数的特点，又进一步提出基于时变遗忘因子的子空间建模方法。

节能运行控制的目标就是寻找一系列列车运行方式的转换点，将列车运行的各个区间联系起来，同时满足正点的要求。Liu等[7]和Khmelnitsky[8]建立列车运行的最优控制模型，利用庞特里亚金原理分析出列车的最优驾驶工况。Howlett[9]研究具有广义运动方程的列车控制问题中最优驾驶策略的确定问题,利用庞特里亚金原理分析连续控制问题最优策略的必要条件。Ko等[10]针对非线性最优控制问题用动态规划方法寻找能量最小的最优轨迹。Miyatake等[11]分别用动态规划法、梯度法和序列二次规划法得到列车的最佳速度曲线。Wang等[12]以能耗和舒适度为目标，分别用伪谱法和混合整数线性规划方法解决最优控制问题。Lu等[13]提出一种基于距离的列车轨迹搜索模型，在此模型上分别应用蚁群算法、遗传算法和动态规划算法寻找最优列车速度轨迹。Chang等[14]提出一种遗传算法，使用适当的惰行控制优化列车运行能耗，分析出列车惰行区间的变化规律。刘建强等[15]依据高速列车牵引特性和阻力特性曲线，提出一种列车节能运行控制方法，基于此方法求解得到列车运行能量消耗最低所对应的最大速度值。马晓娜等[16]运用萤火虫算法，求解能耗最低的工况转换序列。在满足精确停车与准时性的基础上，使得列车运行能耗指标降低14.33%。宋文婷等[17]充分考虑列车的牵引特性和运行线路条件，构建定时约束下的列车操纵模型，获得能耗最小的运行速度曲线。孟建军等[18]结合列车牵引计算方程和选定的线路约束条件, 运用遗传算法对列车运行的节能曲线和运行曲线多目标优化。王鹏玲等[19]引入自适应遗传算法，在列车满足安全、准点、乘车舒适等约束条件的前提下，寻找各工况转换点，使列车运行能耗最小。曹佳峰等[20]以节能运行为目标，以牵引计算为基础，充分考虑实际运行线路条件，提出两阶段优化方法，分别构建时间约束下的列车节能模型。王月仙[21]研究了关于动车组列车能耗的关键影响因素。

传统的列车运行控制方法都是基于固定模型的，不能适应于列车复杂的运行条件，并且未能充分利用列车运行的海量重复性数据。因此，基于人工智能中的强化学习方法，提出一种基于Q学习算法的列车节能驾驶控制算法，将列车运行的速度-位移状态空间离散化，建立列车运行状态的能耗和时间奖励计算方法，进而根据列车状态值函数确定列车最优驾驶策略。

1 基于Q学习算法的高速铁路列车节能优化分析

1.1 构建列车节能优化控制模型

将高速列车看作一个刚体，假设列车是单质点模型，以列车能耗优化为目标，考虑牵引力和制动力限制、线路限速、站间运行时间等约束，构建列车节能优化控制模型。

（1）构建单质点列车动力学模型。根据牛顿力学原理，单质点列车动力学模型可表示为

式中：s为距离，m；t为列车运行时间，s；v为列车运行速度，m/s；m为列车质量，kg；f(s)为当前位置列车施加的牵引力，N；g(s)为当前位置列车施加的制动力，N；r(v)为列车包含滚动摩擦阻力和空气阻力在内的基本阻力，可由戴维斯方程表示为r(v)= av2+ bv + c，其中a，b，c是由车辆确定的特性参数；ra(s)为线路附加阻力，一般包括坡道附加阻力和曲线附加阻力，可表示为ra(s) =mgu(s) +p(s)，其中u(s)为线路坡度，g为重力加速度常数，p(s)为曲线附加阻力。

（2）构建列车节能优化目标函数。列车牵引能耗方程可表示为

式中：J为列车的牵引能耗，J；S为列车运行距离，m。

（3）分析列车运行约束条件。列车运行过程中需满足：在初始状态和末状态速度均为零；列车运行过程中速度不得超过规定限速，施加的最大牵引力或制动力应不大于列车能够提供的最大牵引力或最大制动力；列车实际运行时间近似等于规定站间运行时间。

1.2 基于Q学习算法的列车运行能耗优化模型

1.2.1 Q 学习算法

Q学习算法属于强化学习的方法之一，任务的执行者称为决策者，决策者从周围的环境感知当前的状态，根据当前状态选择相应的动作与环境产生交互，环境受到决策者动作的影响，会反馈给决策者一个奖励值和新的状态，决策者根据新得到的状态再采取新的动作，如此循环往复。决策者的目标是在与环境的交互过程中获得最大的总奖励的期望值。Q学习算法主要由3部分组成，具体如下。

（1）基于当前策略π(s)与环境进行交互，得到若干片段及每次与环境交互的奖励rt。

（2）根据这些片段及奖励求取并更新状态动作值函数，其初值可以任意设置，其更新公式为

式中：Qπ

t(St，At)和Qπt+1(St，At)分别为当前t时刻和更新后t+1时刻的状态动作值函数；St为t时刻的状态；At为t时刻的动作；ɑ为学习率；γ为折扣因子。

（3）根据公式 ⑷ 得到的状态动作值函数，对策略进行优化得到更好的策略，优化的规则为：对于任意状态s，均有

式中：S和A为状态和动作的集合；π'(s)为新的策略，其与环境继续交互，将得到新的片段。

（4）以此类推，经过多次迭代后，即可得到最优的策略和最优的状态动作值函数。

1.2.2 基于Q学习算法的列车运行能耗优化模型

列车优化控制要综合考虑运行能耗和运行时间，列车的状态动作值函数包括2部分，分别为关于能耗的值函数(对列车运行到当前状态能耗的评价)和关于时间的值函数(对列车运行到当前状态花费时间的评价)。列车在每一状态可采取的动作由列车当前的最大运行能力决定。列车状态包括当前列车的位置和速度2部分。首先定义每个状态下可采取的动作，采用随机策略选取每个状态下的动作，得到若干片段，选取满足时间要求的片段更新2个值函数，最后将2个值函数进行加权得到该状态动作值函数。根据得到的状态动作值函数采取贪婪策略选取表格中的状态序列，得出列车速度-距离曲线，并计算曲线能耗。步骤如下。

（1）选取可达状态，构建列车状态空间。对于列车的状态空间，从起点开始，距离间隔为m，速度间隔为n，得到满足限速条件的列车状态空间S= (st(xt，vt))，xt为t时刻列车位置；vt为t时刻列车速度；则st(xt，vt)表示t时刻列车的位置和速度。

定义初始状态为s0(x0，v0)，其中x0= 0，v0= 0；定义末状态为sk(xk，vk)，其中xk=S，vk= 0。当前状态st(xt，vt)可达的下一状态st+1(xt+1，vt+1)，需满足

式中：xt和xt+1分别为t和t+1时刻状态下的列车位置；vt和vt+1分别为t和t+1时刻状态下的列车速度；agmax为t到t+ 1时刻列车的最大减速度；afmax为t到t+ 1时刻列车的最大加速度；Δt为t和t+1的时间间隔。

如果2次状态间可达，则列车采取以下节能策略运行至下一状态：①若vt＜vt+1，列车从xt最大加速到vt+1再巡航至xt+1；②若vt=vt+1，列车从xt巡航至xt+1；③若vt＞vt+1，并且vt+1大于从t时刻惰性到t+ 1时刻的速度，则列车先巡航再惰行至xt+1；④若vt＞vt+1，并且vt+1等于从t时刻惰性到t+ 1时刻的速度，则列车惰行至xt+1；⑤若vt＞vt+1，并且vt+1小于从t时刻惰性到t+1时刻的速度，大于从t时刻最大制动到t+1时刻的速度，则列车从xt先惰行再最大制动到xt+1。

2次状态间的能耗可以表示为

2次状态间的时间可以表示为

（2）构建能耗矩阵和时间矩阵。建立能耗矩阵E= (Eij)k×k，Eij表示从状态si转移到状态sj所需的能耗；建立时间矩阵T= (Tij)k×k，Tij表示从状态si转移到状态sj所需的运行时间。如果si和sj2个状态间不可达(如当前状态通过最大加速度或减速度也无法到达下一状态)，则对应的Eij和Tij均定义为无穷大。

（3）构建并更新值函数矩阵。通过随机选取动作策略与列车环境进行交互，得到满足时间要求的片段。建立能耗值函数矩阵Q_E= (Q_Eij)k×k，Q_Eij表示从状态si转移到状态sj的能耗值函数；建立时间值函数矩阵T_E= (T_Eij)k×k，T_Eij表示从状态si转移到状态sj的时间值函数。利用仿真所得片段更新两个值函数。

①根据公式 ⑷，能耗值函数矩阵Q_E更新函数可表示为

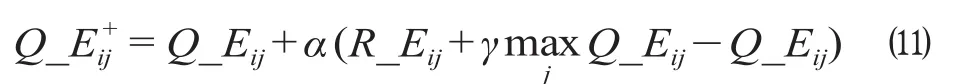
式中：R_E= (R_Eij)k×k为能耗奖励函数矩阵，R_Eij=log (M-Eij)，其中M为换算因子，表示能耗越高能耗奖励越低。

②更新时间值函数矩阵Q_T。初始化Q_T，当列车运行路径中所有时间矩阵值之和满足时间要求，则所有状态的时间值函数加1。不可达状态间的时间值函数为负无穷大。

（4）创建状态动作值函数。对能耗值函数和时间值函数进行加权得到状态动作值函数为

式中：λ为能耗值函数矩阵Q_E的权重系数，用于将能耗和时间值函数平衡为同一数量级。

利用列车最小运行能耗与运行时分一一对应的关系，采用二分法求得最优的λ值，从而得到最优解。

（5）计算能耗值。经步骤（1）至步骤（4），根据选取的状态序列画出列车速度-距离曲线，并计算能耗值。

2 仿真实例

2.1 仿真环境

以京沈客运专线(北京—沈阳)黑山北—阜新站间线路为例，选用CR400BF型动车组列车进行仿真，黑山北—阜新站间线路信息如表1所示，车辆参数如表2所示，黑山北—阜新站间线路坡度值如图2所示，列车基本运行阻力如图3所示。

表1 黑山北—阜新站间线路信息Tab.1 Line information between Heishan North Railway Station and Fuxin Railway Station

表2 车辆参数Tab.2 Parameters of train

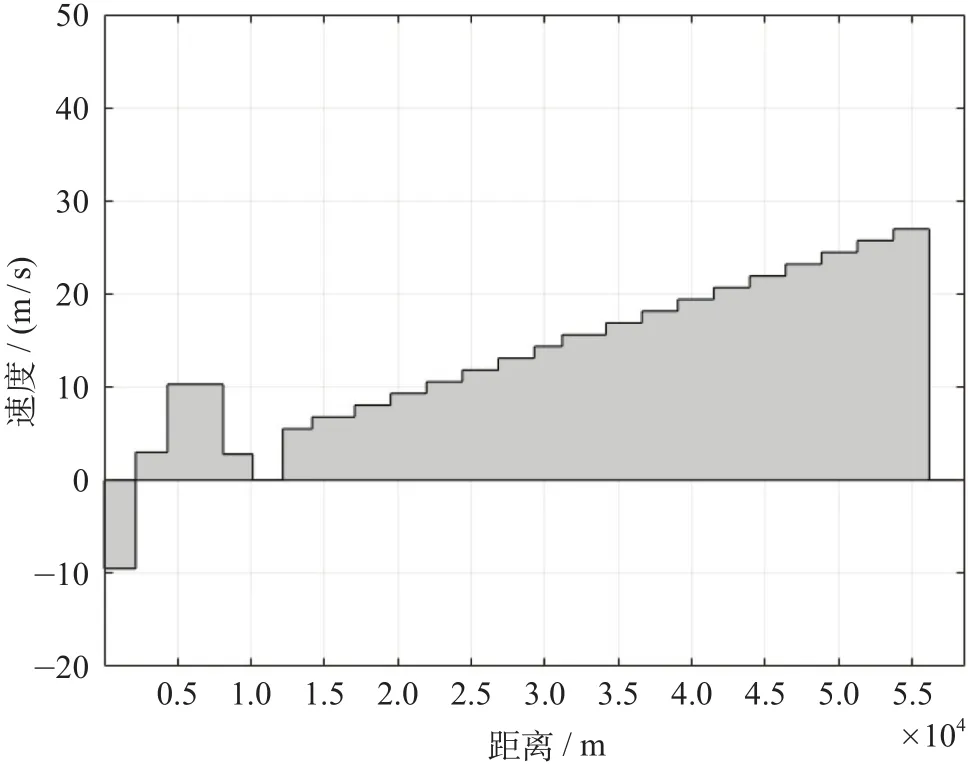
图2 黑山北—阜新站间线路坡度值Fig.2 Line gradient value between Heishan North Railway Station and Fuxin Railway Station

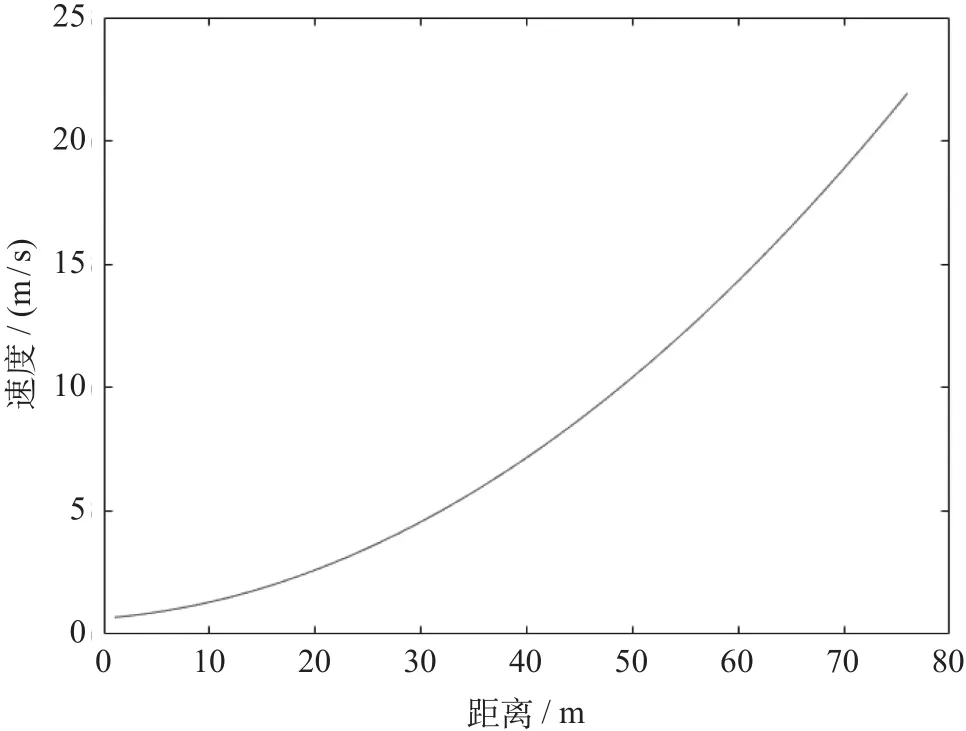
图3 列车基本运行阻力Fig.3 Basic running resistance

将列车看作质点，算法参数如表3所示。

2.2 仿真结果

参数λ与列车运行时分一一对应，因而采用二分法自动求解满足时间要求的λ值。λ与运行时分的关系如图4所示。

表3 算法参数Tab.3 Algorithm parameters

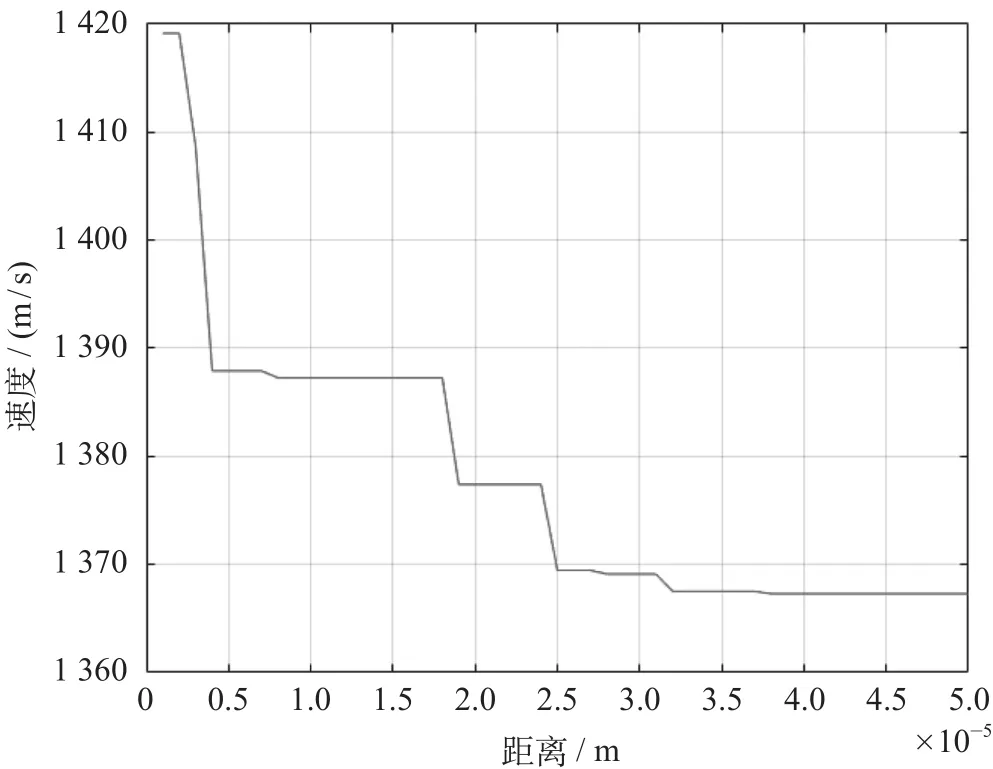
图4 λ与运行时分的关系Fig.4 Relationship of λ and running time

随着时间值函数矩阵的训练次数的增加，算法的有效性能够得到持续提升，仿真结果如表4所示。

采用Q学习算法在时间值函数矩阵训练次数6×106次情况下得到基于Q学习算法(6×106)的列车运行距离-速度曲线如图5所示，在训练次数1×107次情况下得到基于Q学习算法(1×107)的列车运行距离-速度曲线如图6所示。由图6可知，训练次数增加后列车的准时性得到了进一步的提升，运行时间减少了8 s，但能耗仅增加了4%。

采用传统DP算法得到基于DP算法的列车运行距离-速度曲线如图7所示，虽然运行时间减少4 s，但能耗增加了8.8%。

Q学习算法在求最优解的过程中去除了大量的不可达状态，使得其求解空间远小于传统DP算法的求解空间，节省了程序运行时间。同时该算法还具有持续学习的能力，随着训练次数的不断增加求解结果越来越准确与优化。

表4 仿真结果Tab.4 Simulation result

图5 基于Q学习算法(6×106)的列车运行距离-速度曲线Fig.5 Distance-speed curves of train running based on Q-learning algorithm (6×106)

图6 基于Q学习算法(1×107)的列车运行距离-速度曲线Fig.6 Distance-speed curves of train running based on Q-learning algorithm (1×107)

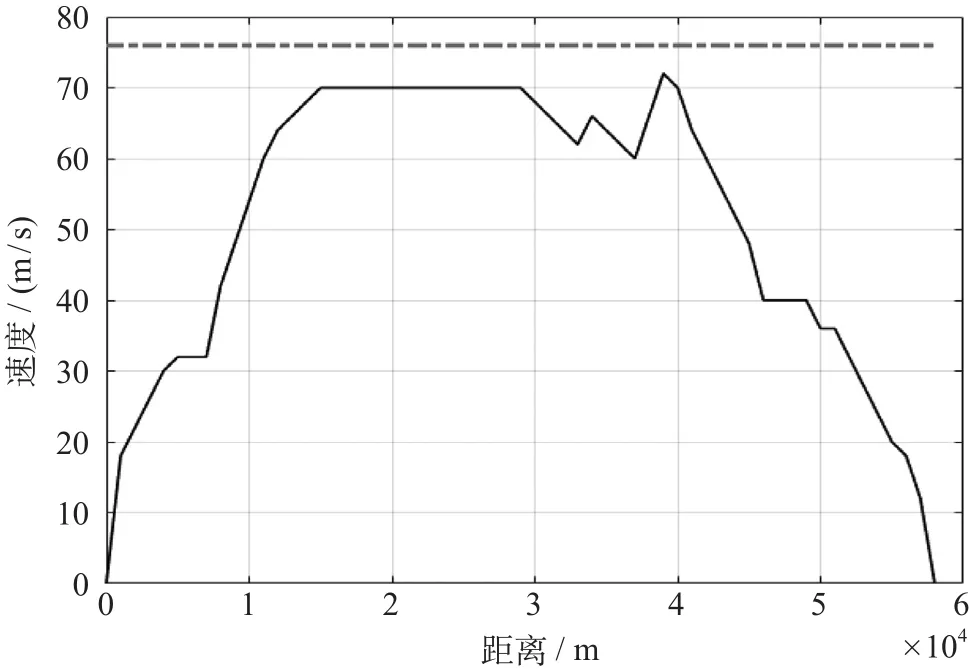
图7 基于DP算法的列车运行距离-速度曲线Fig.7 Distance-speed curves of train running based on DP algorithm

3 结束语

在建立列车节能控制数学模型的基础上，利用Q学习算法求解列车的最优能耗运行策略，突破了传统的基于固定模型的列车运行优化方法，能够适应多种复杂的列车运行环境和线路条件，并充分利用列车历史运行大数据，在满足准时性和乘客舒适度的前提下，有效地减少列车牵引能耗，仿真结果表明该算法较传统DP算法能够在更短的时间内获得更优的节能运行策略。列车智能控制算法集成了现有ATO系统的控制原理和先进的人工智能方法，可以根据不断积累的优秀司机驾驶数据进行优化迭代，在实际列车运行控制系统中具有相当的应用潜力，为未来更智能的列车自动驾驶提供研究思路。