具有非线性发生率且含Ornstein-Uhlenbeck过程的SIS传染病模型
李海燕,韦煜明,彭华勤
( 广西师范大学数学与统计学院,广西桂林 541004)
0 引言
传染病历来是危害人类健康的大敌,用数学模型描述传染病的病理机制已经有很长的历史,其中最经典的模型是Kermack和McKendrick提出的用于描述麻疹、乙肝等传染病的SIR仓室模型[1],让传染病模型进入了定量分析的时代. 随着问题的深入,人们开始研究一些由SIR演化而来的模型[2-4],讨论其动力学性质,得到疾病灭绝的条件.然而,在实际生活中,传染病系统不可避免的受到环境噪声的干扰.因此,越来越多的学者在传染病建模中考虑随机因素的影响,并研究了随机传染病模型的动力学行为[5-8]. 例如Lin等[9]提出了白噪声干预下的随机SIS传染病模型
(1)
其中B(t)为标准布朗运动,σ2>0表示白噪声强度,S(t)表示t时刻易感者人口的数量,I(t)表示t时刻感染者人口的数量, 假设总人口不变,即S(t)+I(t)=N,β表示疾病的传播系数,μ表示自然死亡率,γ表示疾病的恢复率,文献[9]的作者研究了模型(1)中疾病灭绝与持久的条件以及波动强度对疾病产生的影响.张丽萍等人[10]研究了如下具有非线性发生率的随机SIS传染病模型的动力学行为
(2)
其中α是饱和发生率,张丽萍等人利用Feller检测和随机比较原理得到了决定疾病灭绝和持久的随机基本再生数.
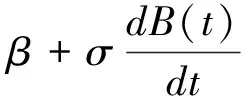
dβ(t)=θ(βe-β(t))dt+ξdB(t),
(3)
其中,θ和ξ为正常数,θ为回复速率,ξ为波动强度,βe为接触系数的长期平均水平.对(3)式积分,得到
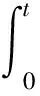
,
(4)
其中,β0∶=β(0).易知β(t)的期望为
E[β(t)]=βe+(β0-βe)e-θt,
(5)
β(t)的方差为
(6)
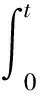
因此,(4)式可写成如下形式
(7)
其中
因为在实际生活中,染病者与易感者的接触率不一定满足双线性关系,即疾病的发生率一般是非线性的,所以本文在[10,11]的基础上,为了更好的描述环境变化对传染病的影响,主要研究一个包含Ornstein-Uhlenbeck过程且具有非线性发生率的随机SIS传染病模型.将(7)式代入到模型(2)中,得到如下随机模型
因为S(t)+I(t)=N,所以只考虑如下方程:
(8)
其中初值I(0)=I0∈(0,N).
基于文献[10]的理论,本文通过构造合适的Lyapunov函数,利用鞅的强大数定理等相关的随机微分方程的知识,讨论SDE模型(8)疾病持久和灭绝的条件,并且研究波动强度和回复速率对疾病的影响.
1 全局正解的存在性和唯一性
对于模型(8)这样一个随机微分方程,首先考虑其解的存在唯一性.本文中记
a∧b=min{a,b},a∨b=max{a,b}.
定理1.1 对任意初值I0∈(0,N)系统(8)存在唯一的正解,并且对所有的t≥0,I(t)依概率1位于(0,N)中.即
P{I(t)∈(0,N)∶t≥0}=1
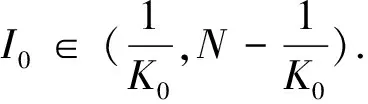
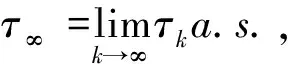
τ∞=∞a.s.,则τe=∞(I(t)∈(0,N)).
现用反证法证明τe=∞a.s..
如果τ∞<∞,则存在T>0和ε∈(0,1)使得P(τ∞≤T)>ε.因此存在一个正整数k1>k0使得对所有的k>k1满足
P(τk≤T)≥ε,
定义一个C2-函数V∶(0,N)→R+如下
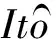
其中
如果β0≤βe,则βe+(β0-βe)e-θt≤βe;如果β0>βe,则βe+(β0-βe)e-θt≤β0.因此
LV(I)≤CV(I)
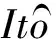
因此
由Grouwall不等式知
EV(I(t∧τk))=V(I0)eCT
(10)
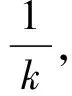
V(I(τk,ω))≥k,
根据(10)式有
V(I0)eCT≥E[XΩk(ω)V(I(τk,ω))]≥kε,
令k→∞,则∞>V(I0)eCT>∞,矛盾,所以τ∞=∞a.s.,即系统(8)存在全局唯一正解.
2 疾病的灭绝性与持久性分析
2.1 疾病的灭绝性分析
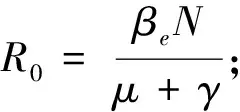
定理2.1 如果
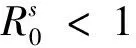
(11)
或
(12)
则对于任意初值I0∈(0,N),SDE模型(8)的疾病灭绝.
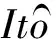
(13)
其中
记
易证
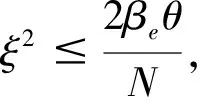
根据(13)式,有
(14)
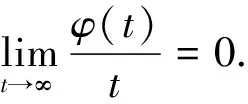
因为
是一个局部鞅,根据鞅的强大数定理[15]知
根据(14)式有
在条件(12)下
同理,根据(13)式有
所以
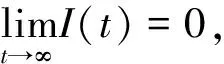
2.2 疾病的随机持久性性分析
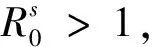
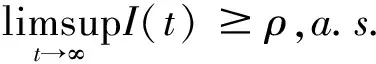
(15)
和

(16)
其中
(17)
是
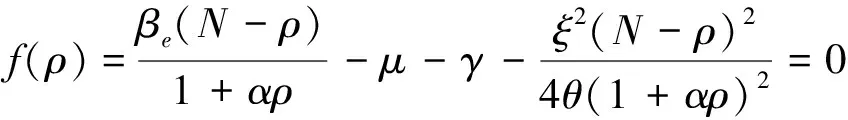
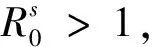
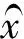
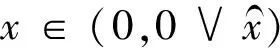
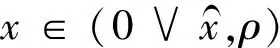
a3)当x∈(ρ,N)时,f(x)<0且严格单调递减.
现在证明(15)式成立,假设(15)式不成立,则存在一个充分小的ε∈(0,1),使得
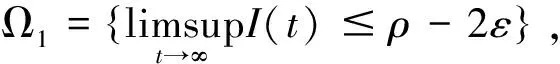
I(t,ω)≤ρ-ε(t≥T(ω)),
(18)
选择充分小的ε使得f(0)>f(ρ-ε).根据a1)a2)和a3)式有
f(I(t,ω))≥f(ρ-ε) (t≥T(ω)),
(19)
根据鞅的强大数定理,存在Ω2∈Ω和P(Ω2)=1,使得对每一个ε∈Ω2,有
(20)
(i)如果β0>βe,则有
现在固定ω∈Ω1∩Ω2,根据(19),(20)两式,对T≥T(ω)时
则有
因此
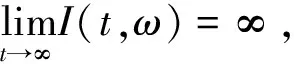
这与(18)式矛盾,所以(15)式成立.
(ii)如果β0<βe,则有
则存在Ω3∈Ω且P(Ω2)=1,使得对每一个ω∈Ω3,
现在固定ω∈Ω1∪Ω2∪Ω3,同样得到
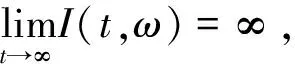
这与(18)式矛盾,所以(15)式成立.
现在证明(16)式,如果(16)式不成立,则存在一个充分小的δ∈(0,1),使得P(Ω4)>δ,其中
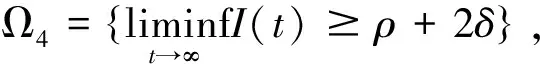
I(t,ω)≥ρ+δ(t≥T(ω))
(21)
根据a2),a3)和(20)式知
f(I(t,ω))≤f(ρ+δ) (t≥T(ω))
(22)
则此时存在一个Ω5⊆Ω且P(Ω5)=1,使得对每个ω∈Ω5,
固定ω∈Ω2∪Ω4∪Ω5,根据(13),(20)和(22)知,对t≥T1(ω)有
综合(21)式,有
因此
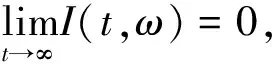
这与(21)式矛盾,从而(16)式成立.
3 波动强度和回复速率对疾病的影响
定理2.1和定理2.2讨论了环境干预下疾病灭绝性和持久性,接下来将讨论波动强度和回复速率对传染病动力学的影响.
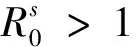
ρ是严格递减的,并且有
和
证明:计算
因为
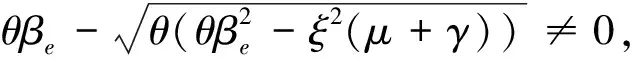
同时有
当R0>2时,
当1 定理3.1得证. ρ是严格单调递增的,并且有 和 证明:计算 因为 因为ρ关于θ是严格单调递增的并且有界,所以有 同时有 当时R0>2, 当1 定理3.2得证. 本文利用随机微分方程的相关知识,讨论了一个具有非线性发生率且含Ornstein-Uhlenbeck过程的随机SIS传染病模型疾病灭绝与持久性的条件.更精确的说,如果θ>θ*或者ξ<ξ*,疾病将持久;如果θ<θ*或者ξ>ξ*,疾病将灭绝.这说明大的波动强度和小的回复速率有助于抑制疾病的爆发,因此,可以通过增大波动强度或减少回复速率来控制疾病的爆发,这在生物学上为疾病的控制提供了理论依据.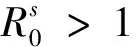
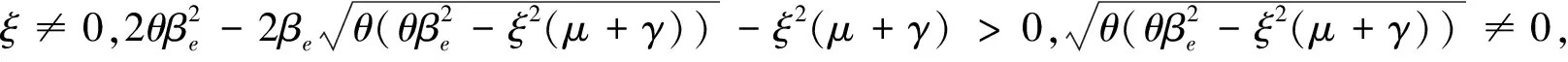
4 结论

