船撞荷载作用下大跨度斜拉桥梁轨相互作用规律研究
左 杨 肖 祥 何雄君
(武汉理工大学交通学院 武汉 430063)
0 引 言
船舶撞击桥梁问题在土木工程界一直得到了较大的关注.Woisin[1]基于结构损伤与变形线性假定的基础上,考虑水流作用得出了具有代表性的船撞荷载.Petersen[2]基于船撞的统计分析与简化数值计算得到了适合于设计分析的船撞力经验公式.此后大量学者对该问题进行了较为深入的分析研究,得出了一系列实用的船撞力计算公式, 并在世界各国形成了设计规范.AASHTO规范基于已有的研究成果,给出了适合于驳船和货船船撞力计算的通用公式[3].我国相关桥梁设计规范也规定了船撞力大小的取值公式[4-5].
梁轨相互作用研究始于Siekmeier对轨道阻力-位移之间的相互关系的理论分析[6].鲍列耶夫柯[7]基于解析法提出了无缝线路纵向附加力的计算公式.文献[8]对桥梁轨道面制动力率和有效制动力率进行多次测试.文献[9]基于提出的准静态分析理论,第一次建立了梁轨相互作用整体分析模型.文献[10]建立了可以模拟纵向力传递过程的理想弹塑性纵向阻力模型,且该模型可采用有限元方法实现.我国对梁轨相互作用的研究先后经历了考虑桥梁伸缩力和挠曲力、计算钢轨纵向位移和钢轨附加应力、考虑纵向阻力与支座类型等多因素对简支梁桥梁轨相互作用的影响,以及桥梁纵向力传递特性等阶段[11].最近,国内外对梁轨相互作用的研究开始采用三维非线性有限元方法建立梁轨一体化模型,这种建立模型的方式能更彻底的研究梁轨相互作用规律.
国内外学者对船撞问题以及梁轨相互作用问题进行了大量的理论分析和实验研究,但在现有梁轨相互作用研究中,多是考虑桥梁伸缩力、挠曲力等附加力影响,并未直接分析船舶撞击下的梁轨相互作用影响,对其作用规律尚不明确,因此,文中以实际大跨度公铁两用斜拉桥为背景,对船撞荷载作用下的梁轨相互作用规律进行了分析研究.基于LS-DYNA3D对船舶撞击荷载进行了有限元动力学分析,接着基于ANSYS结构分析模块分析了常规船撞荷载作用下该桥的梁轨相互作用规律,及不同吨位船撞荷载、不同撞击高度和桥塔下部装有防撞钢套箱时梁轨作用的变化规律.最后,采取合理的防撞方案对防撞效果进行了分析.
1 船撞力分析
1.1 工程背景
以重庆白居寺公铁两用斜拉桥为背景,该桥跨径布置为107 m+255 m+660 m+255 m+107 m,见图1.该桥主塔为水滴形混凝土桥塔,塔高236 m;主梁为板-桁结合钢桁梁,两主桁间距为18 m;每个主塔共设置了40对斜拉索,拉索桥面锚固间距为15 m.

图1 桥梁结构图(单位:cm)
1.2 船撞力时程曲线
根据该公铁两用斜拉桥所在航道的通航要求,该斜拉桥应能承受5 000 t级货船撞击.为研究该斜拉桥在船舶撞击荷载作用下的梁轨相互作用,选取3 000 t级和5 000 t级船舶两种船型作为代表船型,代表船型相关参数见表1.

表1 代表船型参数
基于LS-DYNA3D通用程序模拟船舶撞击桥梁的过程,仿真模型见图2a).仿真建模过程中,为保证船首结构刚度的准确性,船首结构根据实际尺寸进行建模,船身部分采用二维刚体建模方式进行简化,整船质量通过调整材料密度来实现.附加水质量取船舶质量的4%(一般取2%~7%船体质量),并采用提高船体钢材密度方式实现.船舶-桥梁刚度比较小时,桩土效应对船桥碰撞过程及碰撞力影响较小,因此,采用塔墩底部固结的边界条件以忽略桩土效应的影响.船首结构与桥梁塔墩的接触方式采用面面接触.船桥碰撞属于钢与混凝土之间的摩擦,模型中动、静摩擦系数取0.3,且不随压力变化.船首结构部分在撞击过程中将会发生大变形,因此,钢材选用KINEMATIC材料模型,该种模型适用于碰撞荷载作用下金属材料的模拟.桥塔混凝土材料为C40,采用HJC本构模型进行模拟.
在基于LS-DYNA3D的仿真分析中,船舶撞击速度取4.5 m/s,并选取桥轴线的法线与撞击速度方向的夹角为0°以模拟船舶正面撞击斜拉桥的典型最不利情况.模拟船桥碰撞后得到的3 000 t和5 000 t级船舶撞击力的时程数据,见图2b).由图2b)可知,3 000 t级船舶正撞力在0.355 s达到最大值27.8 MN,5 000 t级船舶正撞力在0.585 s达到最大值34.4 MN,且5 000 t级船舶撞击桥梁的持续时间明显更长.
由仿真分析可得到的3 000 t级、5 000 t级船舶的最大撞击力及最大值时间周期,利用经验公式及规范公式亦可得到最大撞击力及最大值时间周期的计算结果,见表2.由表2可知,利用沃辛公式计算的船撞力数值最大,采用LS-DYNA3D模拟船舶撞击桥梁得到的船撞力数值介于沃辛公式和AASHTO规范公式的计算结果之间,但明显大于其他规范公式的计算结果,因此研究采用LS-DYNA3D模拟船舶撞击桥梁得到的船撞力是基本合理的.基于此,采用LS-DYNA3D模拟船舶撞击桥梁,进而得到各种撞击角度、撞击高度的船撞时程荷载.
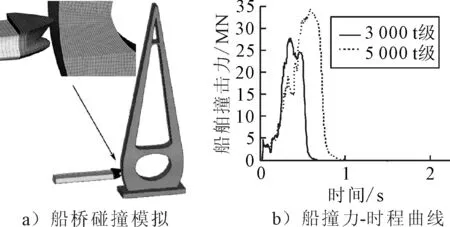
图2 船桥碰撞模拟及船撞力图
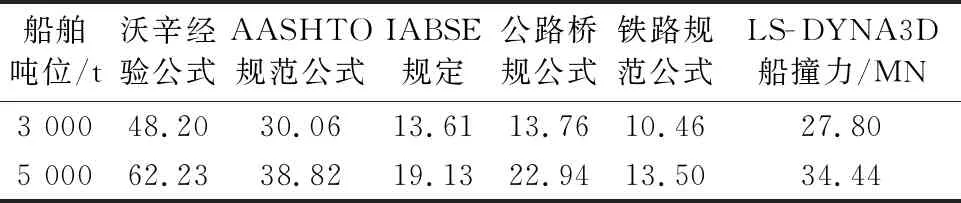
表2 船撞力对比结果MN
2 斜拉桥模型
基于ANSYS有限元软件结构分析模块,并将桥塔下部结构进行了简化,建立该斜拉桥全桥有限元模型见图3.模型中取顺桥向为X方向、竖桥向为Y方向、横桥向为Z方向,采用BEAM4单元模拟主桁架、主塔、轨道纵梁和钢轨.考虑LINK10单元具有双线性刚度矩阵特性,单元受压时刚度就会消失,其可以模拟轴向仅受拉或仅受压杆单元,因此选取LINK10单元模拟松弛状态下的斜拉索,并且采用等效弹性模量法考虑斜拉索的垂度引起的非线性影响;采用SHELL63单元模拟上下层钢正交异性桥面板.
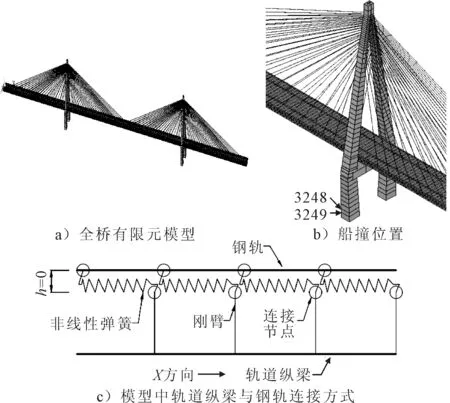
图3 斜拉桥有限元模型图
ANSYS建模过程中,为合理模拟线路-纵梁之间的相互作用,采用细化纵梁和钢轨的节点划分,每隔0.75 m建立一个节点;在桥头两端分别建立伸出钢桁架梁240 m的钢轨,并在钢轨端点处进行固结以减小路基的影响.为保证钢轨的空间线形,可通过采用带刚臂的纵梁来模拟梁轨相互作用;对于纵梁和钢轨之间的纵向阻力,可通过刚臂和钢轨在X方向采用COMBIN39非线性弹簧单元连接,在Y,Z两个方向以耦合方式连接.由于钢轨截面面积较小,可忽略其转动,因此约束钢轨绕X方向的转动.全桥模型共采用了16 000个BEAM4单元,160个LINK10单元,920个SHELL63单元,3 682个COMBIN39单元.
3 船撞荷载作用下的梁轨相互作用
3.1 5 000 t级船撞荷载作用下的梁轨相互作用分析
根据该斜拉桥所在航道的通航要求,航道最高通航水位为198.25 m,最低通航水位为166.84 m,最高和最低通航水位分别对应于有限元模型节点为3248和3249高度处.纵梁与钢轨横向相对位移反应了纵梁对钢轨的约束力的大小,直接反应梁轨相互作用的情况.
选取5 000 t级船舶作为代表船型,船舶撞击位置选择船舶在航道上能正常航行的最低通航水位所对应的3249号节点,针对该撞击荷载进行数值计算,并选取跨中、1/4跨作为梁轨相互作用的研究断面,得到其横向梁轨相对位移值见图4.由图4可知,5 000 t级船撞荷载作用下,梁轨横向相对位移值在跨中和1/4跨断面处数值差异较小,其最大相对位移值均小于2.0 mm,说明梁轨横桥向变化趋势基本一致.

图4 5 000 t级船撞荷载作用下横向梁轨相对位移值
3.2 不同船撞荷载作用下梁轨相互作用分析
选取3 000 t和5 000 t级两种船撞荷载,船舶撞击位置选择3249号节点.主要分析两种船撞荷载作用下,梁轨跨中、1/4跨断面处的横向相对位移变化规律,见图5.由图5可知:①两种船撞力作用下的梁轨跨中和1/4跨节点相对位移值波动范围为-2.0~2.0 mm,说明船撞力的大小对梁轨相对位移值变化趋势的影响并不大;②梁轨相对位移值受船撞力大小影响较大,且船撞力越大,梁轨相对位移越大.
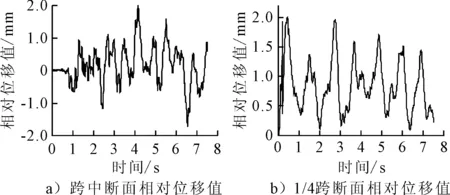
图5 两种船撞荷载下梁轨横向相对位移值
3.3 船舶撞击桥梁不同高度时梁轨相互作用分析
选取5 000 t级船舶作为代表船型,船舶撞击桥梁位置选取3248号节点和3249号节点,主要对梁轨跨中断面处横向相对位移值变化规律进行研究,见图6.由图6可知,船撞荷载作用桥塔下部不同高度情况下,梁轨跨中节点的横向相对位移值最大值接近3.0 mm,说明船撞点的高低对铁轨的位移有较大的影响,且船撞点越高,其对位移大小的影响越显著.

图6 不同高度时梁轨Z向相对位移值
3.4 防撞装置对梁轨相互作用影响规律分析
船桥碰撞时,当桥梁未安装防撞设施,梁轨相对位移最大值接近2.0 mm;若梁轨相对位移继续扩大将会造成桥梁线路结构的破坏,如桥上混凝土轨枕的开裂,甚至是钢轨扣件的损坏等线路结构损伤问题.因此,为保护桥梁线路结构在正常运营期间的安全,有必要对桥梁安装防撞设施时梁轨相对作用进行讨论研究,
为研究防撞装置的防撞效果,选取钢-泡沫铝填充结构作为防撞装置,并将其安装于桥塔下部适当位置.基于LS-DYNA3D对安装防撞装置后的船撞桥进行仿真模拟,有限元模型见图7a),最终计算分析得到船撞力时程曲线见图7b).由图7可知,带有防撞钢套箱时其船撞力最大值接近20 MN,相比于裸墩有很明显的减小,减小幅度达到42.8%,但时间周期明显增大.将带有防撞钢套箱时的船撞力作用于该斜拉桥模型,选取3249号节点作为撞击位置,得到典型断面梁轨横向的相对位移见图8.桥梁跨中的梁轨相互作用对桥上整个轨道结构而言,较为重要.由图8a)可知,安装防撞钢套箱时,桥梁跨中的横向最大梁轨相对位移显著小于2.0 mm,相对于裸塔有非常显著的减小,说明防撞设施对于桥梁跨中的轨道结构的保护作用很明显.此外,由图8b)可知,1/4跨处的横向最大梁轨相对位移也显著减小,其效果较跨中处稍差,这也与防装设计以跨中作为控制断面有关.

图7 带有防撞装置的船桥碰撞模拟及船撞力图

图8 5 000 t级船撞荷载作用下梁轨横向相对位移
4 结 论
1) 根据LS-DYNA3D通用程序模拟得到的船撞力,经过与经验公式和规范公式对比后是合理的;模拟船桥碰撞过程中,船舶吨位的大小对船撞力的大小有比较明显的影响,既影响碰撞持续时间,也影响船撞力最大值出现的时间周期.
2) 船舶撞击桥梁时,桥梁及桥上轨道结构会出现比较明显的位移,并且船撞力的大小、船舶撞击高度等对梁轨相对位移有不可忽视的影响.
3) 梁轨相互作用分析研究表明,船桥碰撞过程中,在桥梁结构适当位置安装防撞装置后,船桥碰撞过程中传递至桥梁的能量被部分消耗掉,使梁轨相对位移有了显著的减小,从而在一定程度上能更有效的保护桥梁的安全.
因此建议在桥梁适当位置设置防撞装置或缓冲消能设施,使船舶撞击桥梁对桥上轨道结构的影响减小,从而不影响桥梁的正常使用.

