基于改进支持向量机的工程造价预测模型∗

朱琳 刘春

（四川建筑职业技术学院网络管理中心 德阳 618000）

1 引言

造价预测对工程费用、工程计划等都有影响，在工程管理领域具有十分重要地位，因此工程造价预测一直是人们关注的焦点［1］。在工程造价预测过程中，由于受到多种因素的影响，工程造价预测的建模过程十分复杂，因此工程造价预测也是工程管理研究中的一个难点，成为当前一个重要的研究方向［2］。

针对工程造价预测问题，国内外许多学者和专家进行了深入研究，提出许多工程造价预测模型［3～5］。当前工程造价预测模型可以划分为两大类：传统模型和现代模型，其中传统模型主要包括定额法、工程量清单法等［6］，其中定额法根据国家发布的预算定额对工程造价进行预测，该模型的工程造价预测结果不会过低或者过高，预测错误较小，但是该方法没有考虑市场竞争因素、人为因素以及技术改进因素，而且建模和预测的效率十分低，不适应大工程的造价预测［7～8］。工程量清单法是针对定额法的不足提出来的，实际应用中由于没有考虑企业之间的恶性竞争，工程造价预测的误差大，缺陷十分明显［9～10］。现代工程造价预测模型又划分为两类：线性模型和非线性模型，其中线性模型主要包括模糊数学模型、多元线性回归模型，工程造价变化具有一定的随机性和非线性，而线性模型不能刻画工程造价的非线性变化特点，工程造价预测误差高［11］。非线性模型主要包括各种神经网络和支持向量机，神经网络虽然具有很好的非线性拟合能力，但只有在训练样本数量大的条件下才能展现出高精度的非线性拟合结果，当训练样本不足时，工程造价的预测误差大，同时神经网络的结构又十分复杂，学习速度慢［12］。支持向量机没有训练样本数量大的限制条件，在训练样本不足的情况下也可以得到较好的工程造价预测结果，但存在学习速度慢的缺陷［13～14］。最小二乘支持向量机是一种改进的支持向量机，克服了神经网络要求训练样本数量大的缺陷，在许多非线性预测领域得到了成功的应用，同时也为工程造价预测提供了一种新的建模工具［15］。

针对当前工程造价预测模型存在的预测精度低、建模效率低等不足，提出了基于改进支持向量机的工程造价预测模型，并采用在Matlab 2014R工具箱实现了工程造价预测的仿真对比实验，结果表明，改进支持向量机大幅度提高了工程造价预测精度，而且工程造价整体预测性能要明显优于对比模型，具有更高的实际应用价值。

2 相关理论

2.1 改进支持向量机

支持向量机具有良好的泛化能力，不存在神经网络等智能优化算法存在的过拟合缺陷，但学习速度相当慢，建模效率低，为此有学者提出了一种改进的支持向量机——最小二乘支持向量机。相对于支持向量机，最小二乘支持向量机的优势主要表现在：1）约束条件改为等式，简化了学习过程，学习速度明显加快；2）误差损失结果作为训练结果的评价指标，改善了回归效果。对于样本集：D={(xk，yk)|k=1，2，…N } ，采用径向基函数作为最小二乘支持向量机的核函数Ψ(⋅，⋅)，定义为

式中，σ表示核宽度。

从最小二乘支持向量机的工作过程可以发现，其需要确定两个参数，而支持向量机回归过程中需要确定3个参数，最小二乘支持向量机的建模速度大幅度提升。最小二乘支持向量机的回归目标优化函数为

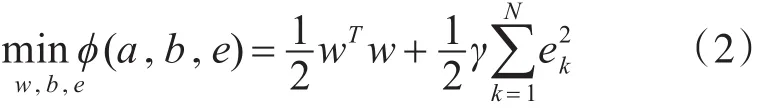
其中，γ表示惩罚系数，式（2）的约束条件为

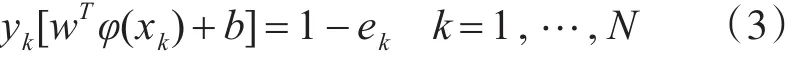
为了解决式（2）问题，引入拉格朗日乘子法建立如下等式：

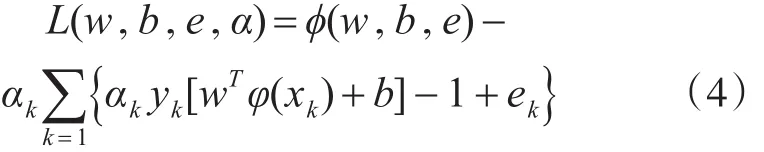
式中，αk∈R为拉格朗日乘子。

式（4）优化的条件是w，b，ek，αk的偏导数为零，即有

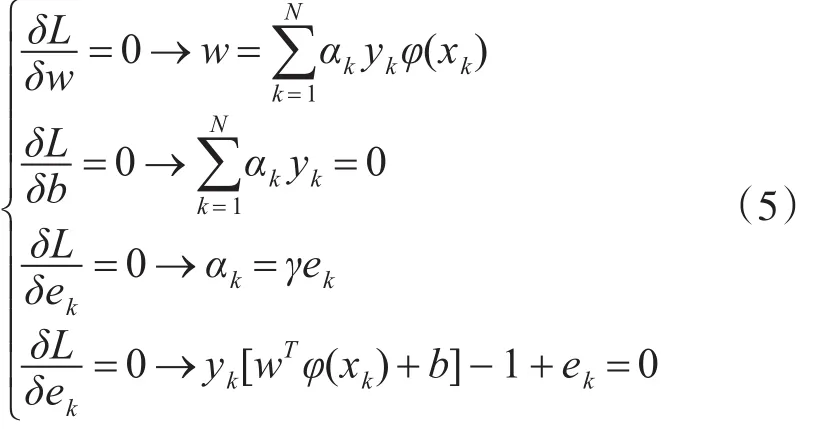
这样式（4）可以转变式（6）的求解过程。

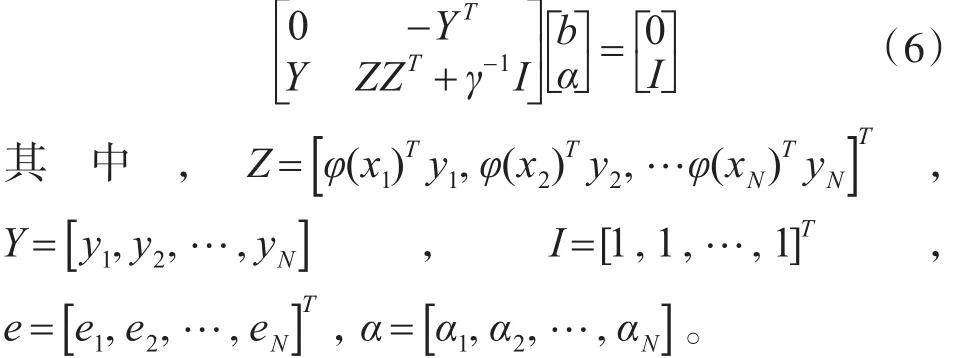
根据Mercer理论和Ω=ZZT可以得到

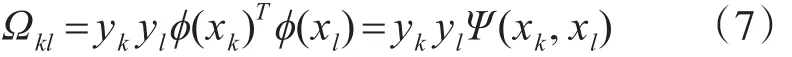
最小二乘支持向量机的最优回归函数为

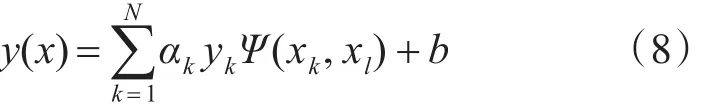
2.2 粒子群优化算法

受到鸟群捕食行为的启发，有学者提出了粒子群优化算法。每个粒子代表解空间中的一个解，粒子当前搜索的最优解为个体极值（pbest），而粒子群当前搜索的最优解为全局极值（gbest）。在实际应用中，适应度函数的值用于衡量粒子的优劣程度，而且每个粒子均根据自身和群体极值不断更新自己状态，从而产生新一代粒子群。

设粒子群中的粒子数为M，第i（i=1，2，…，M）个粒子的位置为xi，其当前最优位置为pbest［i］，对应的速度为vi，粒子群的当前最好位置为g，那么在第t+1时刻，可以根据式（9）和（10）更新粒子i的状态：

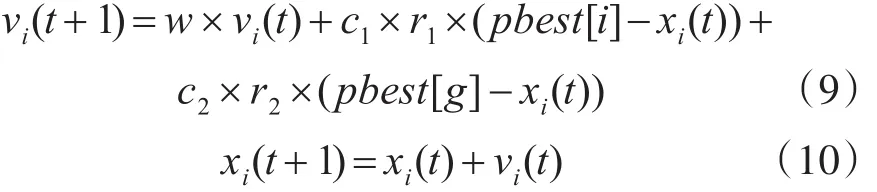
式中，c1，c2为学习因子，r1和r2是［0，1］上的随机数；w为惯性权重，w的调整方式为

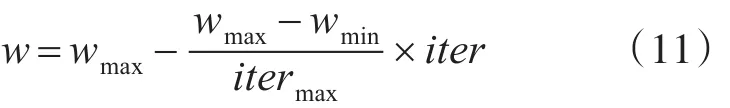
式中，iter表示迭代次数。

3 改进支持向量机的工程造价预测模型

1）收集工程造价历史数据，由于历史数据变化范围大，对工程造价建模过程具有一定的干扰，为此做如下处理。

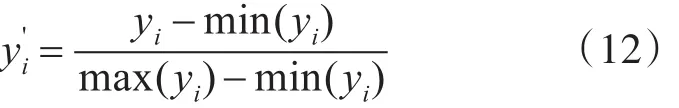
2）将处理后的工程造价数据划分为两部分：训练样本和测试样本，训练样本用于改进支持向量机的学习，建立工程造价预测模型，测试样本用于分析工程造价模型的泛化性能。

3）将训练样本输入到改进支持向量机中进行学习。

4）采用粒子群算法优化改进支持向量机的参数γ和σ的值，建立工程造价预测的回归模型。

5）采用建立好的工程造价预测模型对工程造价的测试样本进行预测，并分析工程造价预测模型的泛化性能。

基于改进支持向量机的工程造价预测模型的工作流程如图1所示。

图1 改进支持向量机的工程造价预测流程

4 仿真实验

4.1 源数据

采用某市2015-2018年的工程造价数据作为实验数据，去掉一些无用数据，共得到150个数据点，工程造价数据具体如图2所示。采用Matlab 2014R工具箱实现了工程造价预测的仿真实验。

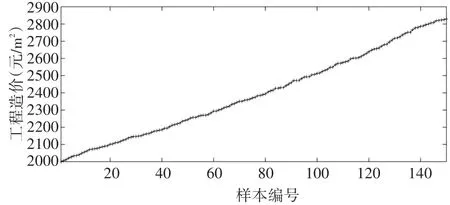
图2 实验数据

4.2 结果与分析

选择最后50个样本作为工程造价的测试样本，其余工程造价样本作为训练样本，采用粒子群优化算法确定改进支持向量机的参数γ＝100.175，σ=1.974，建立工程造价预测模型，然后对工程造价测试样本进行预测，得到如图3所示的预测结果。工程造价的预测偏差如图4所示，对图3和图4的预测结果进行分析可以清楚看出，改进支持向量机可以描述工程造价的实际变化特点，可以很好地捕捉工程造价的变化趋势，预测偏差相当小，可以忽略不计，从而得到了十分理想的工程造价预测结果。

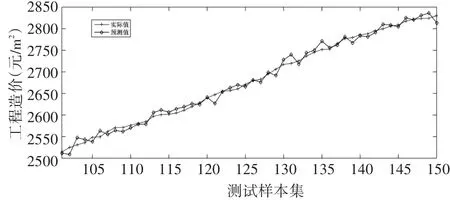
图3 改进支持向量机的工程造价预测结果

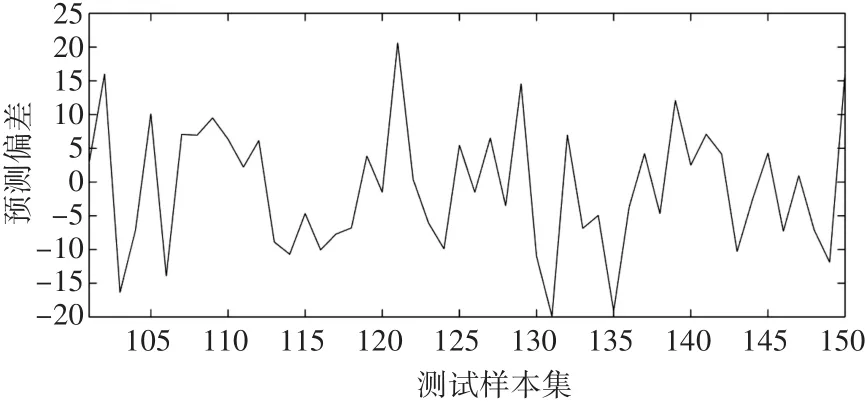
图4 改进支持向量机的工程造价预测偏差

为了验证改进支持向量机的工程造价预测结果优越性，设计了几种对比模型：1）支持向量机的工程造价预测模型（SVM）；2）BP神经网络的工程造价预测模型（BPNN）；3）多元线性回归的工程造价预测模型（MLR）。全部工程造价预测模型的预测精度、预测误差以及平均建模时间（秒，s）如表1所示，对表1的实验结果进行分析，可以知道：

1）MLR的工程造价预测精度最低，预测误差最大，这是因为MLR是一种线性建模方法，只能描述工程造价的线性变化特点，而无法描述工程造价的非线性变化特点，预测结果不理想。

2）BPNN的工程造价预测精度也偏低，这主要是由于BPNN是一种基于大样本的机器学习算法，预测结果不稳定，出现了许多过拟合的工程造价预测结果，导致工程造价预测误差偏大。

3）SVM的工程造价预测精度比较高，而且工程造价预测误差相当的小，但是平均建模时间长，使得工程造价预测的建模效率低。

4）改进支持向量机的工程造价整体预测性能最优，相对于对比模型，具有十分明显的优越性，对比结果也验证了本文模型用于工程造价建模和预测的优越性。

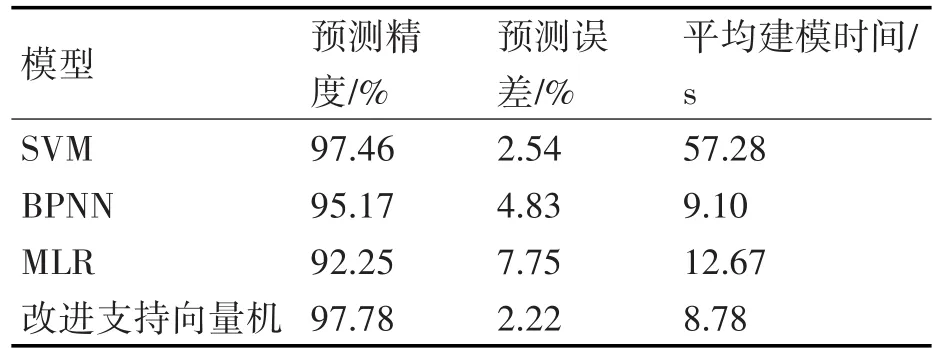
表1 与其它模型的工程造价预测结果对比

5 结语

工程造价预测建模具有重要的实际应用价值，针对当前模型无法准确描述工程造价非线性变化特点的局限性，提出了基于改进支持向量机的工程造价预测模型，采用最小二乘支持向量机强大的非线性建模能力对工程造价的变化特点进行拟合，并引入粒子群算法对工程造价预测模型的参数进行在线性优化，工程造价预测的仿真实验结果表明，改进支持向量机可以准确从工程造价历史数据中挖掘到工程造价变化趋势，能够获得了高精度的工程造价预测结果，同时提高了工程造价的建模效率，整体性能要显著优于其它工程造价预测模型，在工程管理中具有广泛的应用前景。