线性时滞系统稳定性自动化控制方法研究

周秋坤，刘 桦，陈剑雪，段倩倩，郭海泉

（上海工程技术大学 电子电气工程学院，上海 201600）

0 引言

从线性时滞系统理论观点出发，任何系统当前状态变化都会不可避免的受到外界干扰影响，这种影响称之为时滞，具有时滞属性的系统被称为时滞系统。对于线性时滞系统来说，系统功能研究是建立在该系统稳定性基础上的，但在实际生活中由于环境变化等因素难免会存在一些无法避免的时滞问题，这种问题的产生在很大程度上会导致系统功能性差，甚至出现不稳定现象[1]。因此，线性时滞系统稳定性研究是从时滞系统基本点出发的，同时研究线性时滞系统稳定性判据也是控制该系统的重点。稳定性是控制系统重要特征之一，因此，研究时滞系统控制方法可使线性时滞系统处于稳定状态。目前，有关线性时滞系统的问题正在研究中，随着MATLAB工具箱的不断完善，需将研究重心转移到线性时滞系统稳定性自动化控制中[2]。

当前，针对线性时滞系统稳定性自动化控制方法主要有两条主线，分别是频域和时域，时滞系统分析是在频率域中进行的，此时需要一个超越方程，求解过程相对比较复杂，尤其是在系统存在不确定因素时求解更为复杂。文献[3]提出一种不确定线性时滞系统模型参考自适应控制方法，采用差分方程增广处理系统的状态变量，同时将时滞系统动力学方程转变为增广状态方程。参考得到的时滞系统动力学方程构建相应的参考模型，最后运用模型控制律，确保闭环参考模型系统的稳定性。分析实验结果可知，该方法能够在时滞不确定的情况下，实现对系统的控制。但是由于没有考虑到线性时滞系统稳定性分析问题，导致控制效果较差。文献[4]提出前提不匹配的模糊时滞系统的稳定与控制方法，依据线性矩阵不等式给出保守性较小的时滞依赖的稳定性准则。在此基础上结合不匹配策略，设计模糊状态反馈控制器，运用该控制器实现对时滞系统稳定性的控制。分析实验结果可知，该方法下的线性时滞系统与实际控制下的运行轨迹存在一定的偏差，控制效果不理想。

根据上述分析可知，研究控制线性时滞系统稳定性的方法是具有必要性的，本文对时滞系统稳定性分析做了详细描述，也总结了相关成果，考虑外界干扰，提出了基于轨迹跟踪的线性时滞系统稳定性自动化控制方法。

1 问题描述

在进行线性时滞系统稳定性自动化控制之前需要充分考虑具有代表性的状态线性时滞系统：

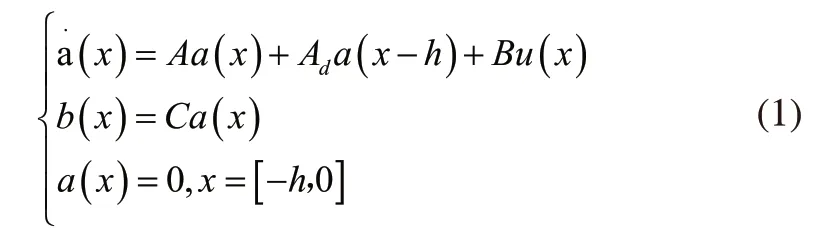
式(1)中：a(x)表示线性时滞系统状态；u(x)表示线性时滞系统控制输入；b(x)表示线性时滞系统控制输出。标量h为线性时滞系统常数时滞；A、Ad、B、C表示已知的适当维数实数矩阵。

根据式(1)，设计状态反馈矩阵：

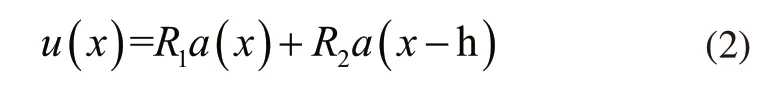
式(2)中：R1、R2表示状态反馈矩阵参数。

1）当R1≠0、R2=0时，为无记忆状态反馈矩阵；

2）当R1=0、R2=0时，为有记忆状态反馈矩阵。

因此，无记忆状态反馈矩阵是有记忆状态反馈矩阵的特殊表现形式[5]。

根据问题描述得出，本文研究主要包括两个方面：一是针对线性时滞系统进行稳定性分析，使得系统对于任何常数都具备满足渐近稳定的条件；二是针对所获取的结论进行仿真研究，验证该结论的有效性[6]。

2 线性时滞系统稳定性分析

根据上述描述的问题，从工程实践角度分析，线性时滞系统的存在往往会导致系统失去稳定性。线性时滞系统稳定性分析流程如图1所示。

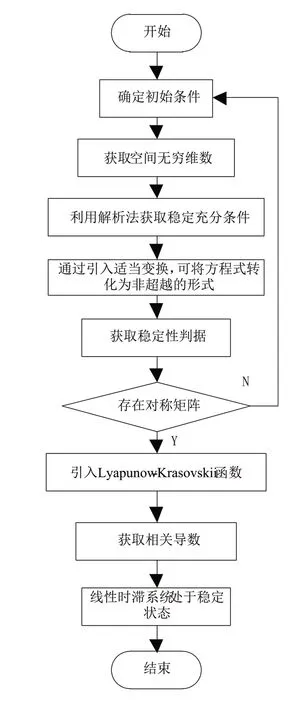
图1 线性时滞系统稳定性分析流程

根据线性时滞系统稳定性分析流程，以单时滞方程为例：

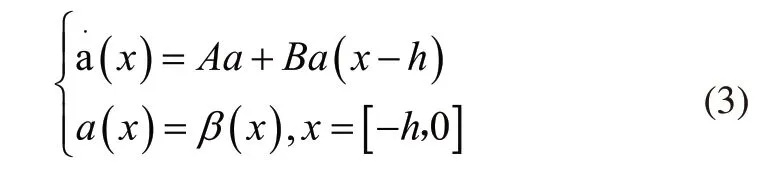
式(3)中，h＞0为线性时滞状态，初始条件是在[-h,0]连续方程式中确定的，线性时滞系统中x＞0的行为不仅仅依赖于0时刻的状态，还与该时间段内的运动息息相关，由此可知解空间具有无穷维数。利用解析法进行相关研究，以此获取稳定充分条件，通过引入适当变换，可将方程式转化为非超越形式，得到稳定性判据[7]。

根据上述分析，选取Lyapunow-Krasovskii泛函如下所示：

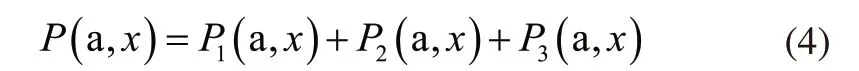
其中：

对称矩阵Q，W，E都为对称正定矩阵，由此可知：

P（a，x）＞0，由上述公式可得：

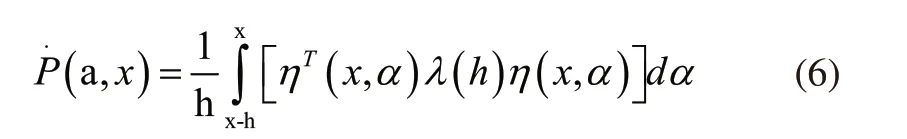
其中：

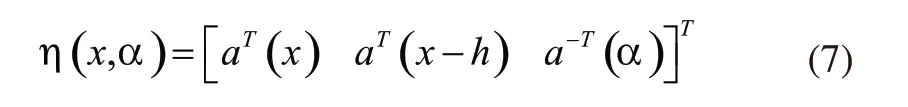
如果式(7)小于0，那么：

即P（a，x）为Lyapunow函数，由上述公式可推断出该函数成立，因此线性时滞系统(1)对所有的（0，范围内都是趋于稳定状态的[11,12]。

3 基于轨迹跟踪的线性时滞系统稳定性自动化控制研究

基于上述内容，提出了基于轨迹跟踪的线性时滞系统稳定性自动化控制研究方法，其基本思路为：根据输出的动态信息以及期望输出轨迹，使用相对简单的学习方式，修正控制输入，并进行迭代控制。在既定时间区域内，经过若干次迭代处理后，可使系统确定精确的目标轨迹[13]。

通过设计容错控制器kf（x），保证线性时滞系统的状态收敛到参考系统状态中，控制器设计方案如图2所示。

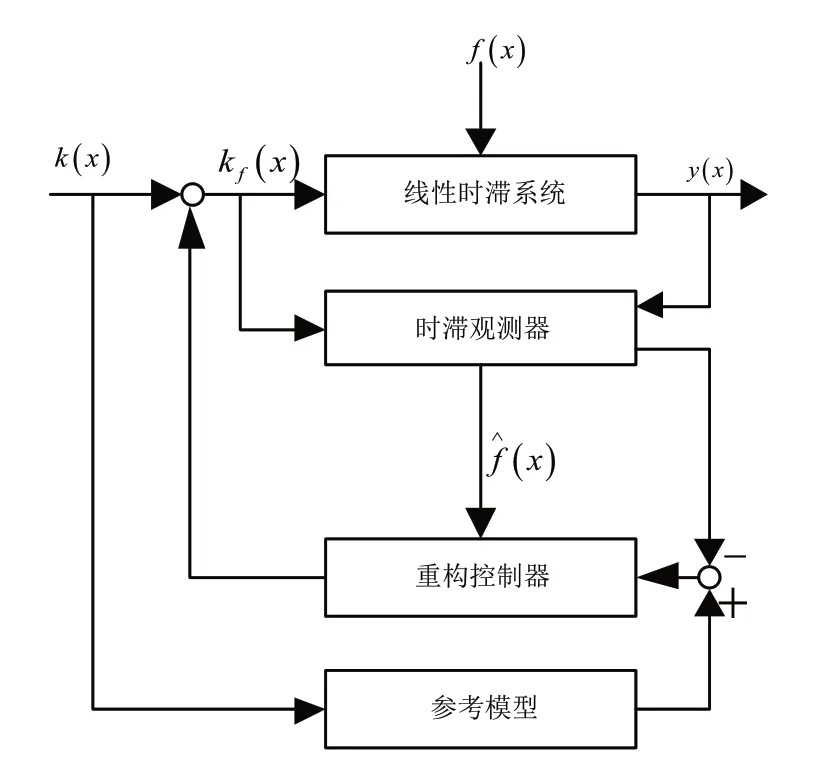
图2 控制器设计方案

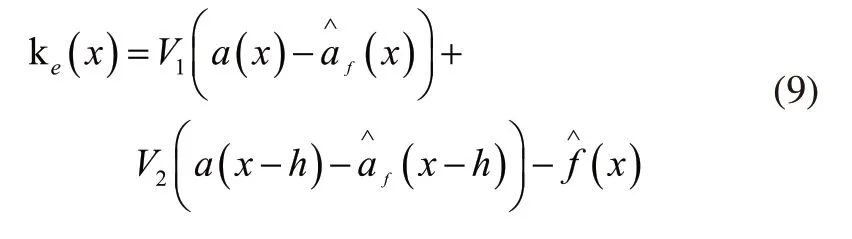
其中，V1、V2表示状态反馈增益矩阵，该矩阵的设立就是为了保证系统稳定性，且在无记忆状态反馈矩阵控制和有记忆状态反馈矩阵控制之间的差值最小化[15]。除此之外，容错控制设计方案还需了解矩阵相关参数，为了估计af(x)和f(x)，需充分考虑观测器。

为了方便描述，在不出现歧义情况下，省略x，在该设计过程中，应先定义状态跟踪误差e1、状态估计误差e2、输入误差e3和控制出现错误估计误差e4以及输出估计误差e5：

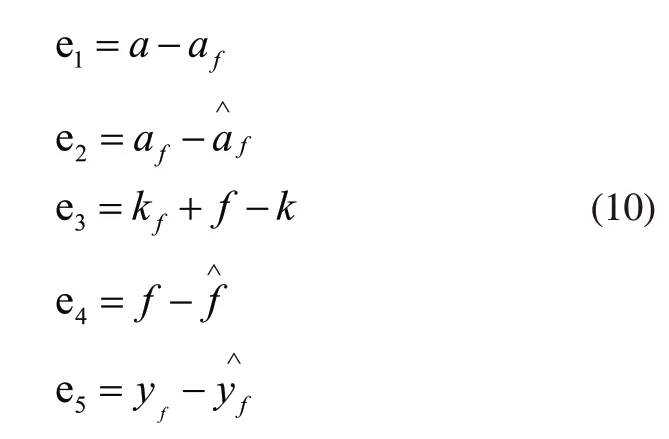
通过上述公式加减m1af、m2af(h)以及f项，可得到：

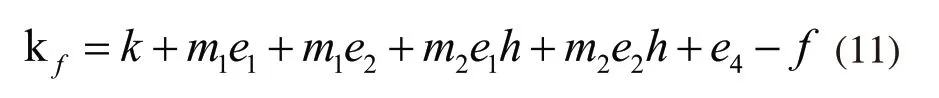
因此，e3可表示为：

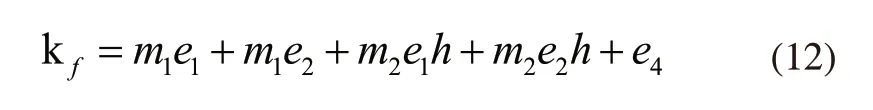
根据上述公式，得到e1和e2导数为：

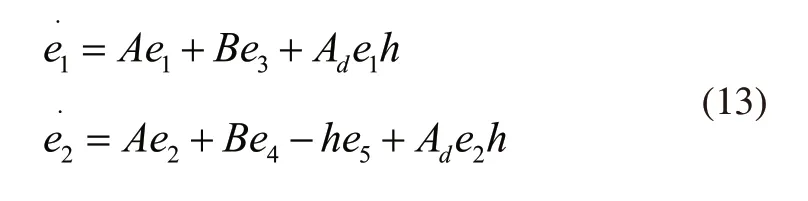
控制出现错误估计误差导数为：

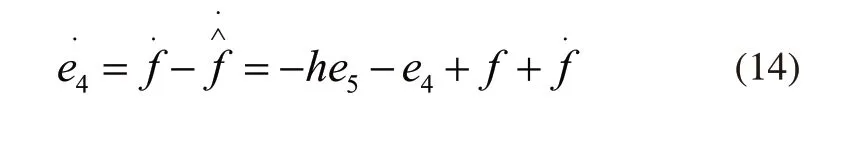
进一步整理，可得到输出误差导数方程：

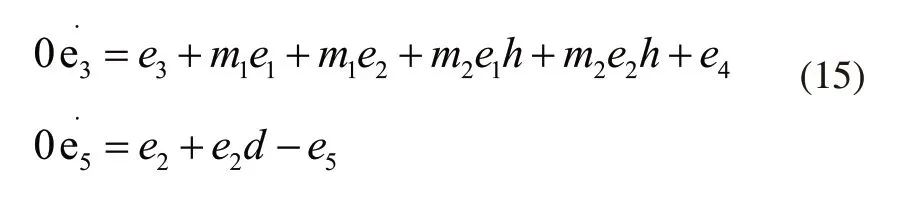
将上述公式组成如下广义系统：

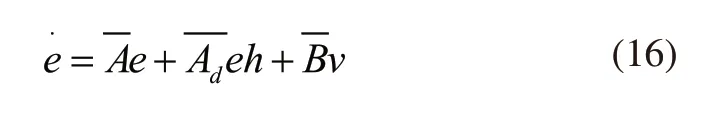
其中：

在已知常数下，如果存在适当维数正定矩阵，则状态跟踪误差e1、状态估计误差e2、输入误差e3和控制出现错误估计误差e4以及输出估计误差e5的增益小于该常数。此时存在Lyapunow-Krasovskii泛函下的广义系统稳定值小于既定界限值，由此完成线性时滞系统稳定性自动化控制。

4 仿真实例

为了验证提出的基于轨迹跟踪的线性时滞系统稳定性自动化控制研究方法有效性，需进行仿真实验分析。充分考虑式(1)形式的线性时滞系统，其系数矩阵如下所示：

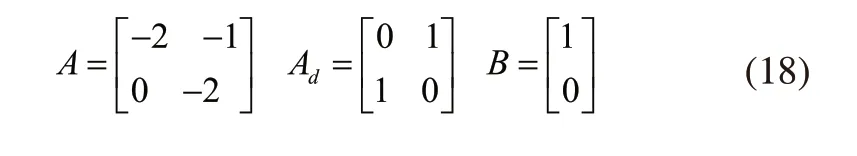
基于此，可得到不同的时滞上界，如表1所示。

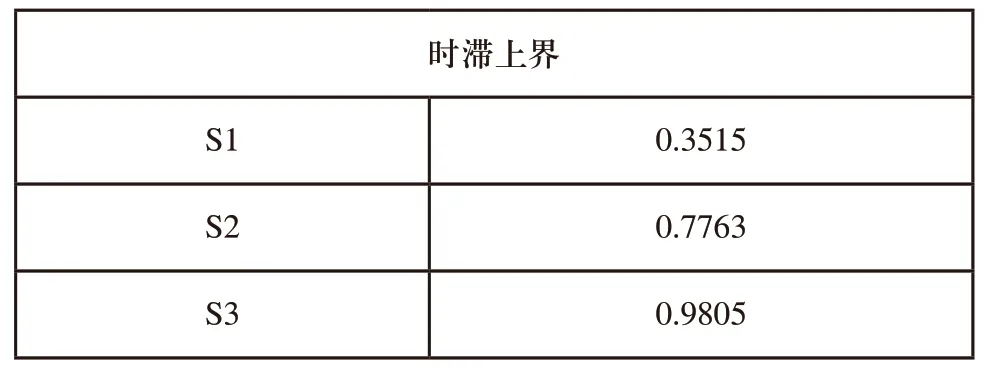
表1 不同的时滞上界

图3 依次为5和10时的线性时滞系统状态曲线

以S3数据为基准，将不确定线性时滞系统模型参考自适应控制方法（文献[3]方法）、前提不匹配的模糊时滞系统的稳定与控制方法（文献[4]方法）与基于轨迹跟踪的控制方法的控制效果进行对比分析，结果如图4所示。

不同方法下的线性时滞系统状态曲线，如图4所示。

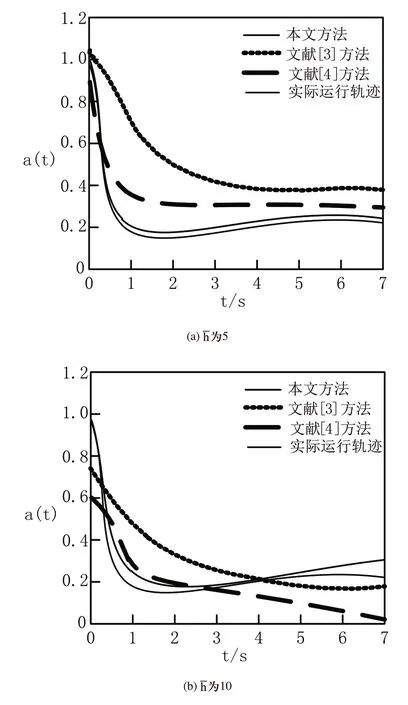
图4 不同方法下的线性时滞系统状态曲线

为了进一步验证本文方法控制效果更好，需将不同方法的控制效果进行对比分析，结果如表2所示。

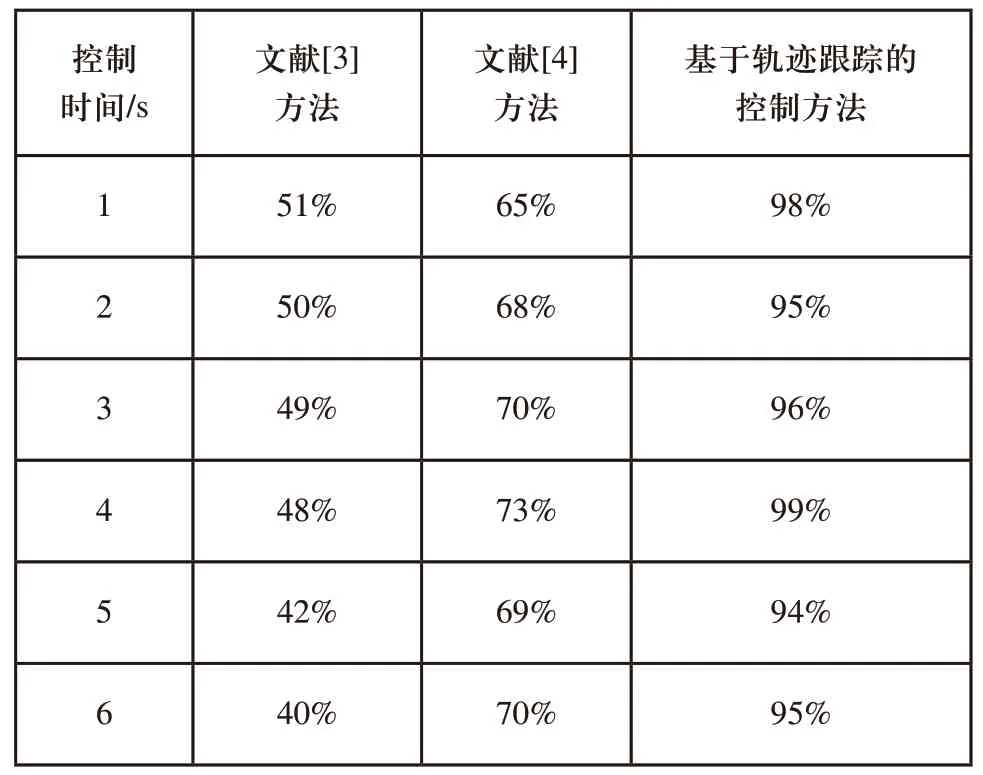
表2 两种方法的控制效果对比分析

根据表2所示对比结果可知，采用文献[3]方法的控制效果始终低于55%，且在控制时间为6s时，该方法控制效果达到最低为40%；采用文献[4]方法的控制效果始终低于73%，且在控制时间为1s时，该方法控制效果达到最低为65%；采用基于轨迹跟踪的控制方法控制效果始终高于90%，且在控制时间为4s时，控制效果达到最高为99%，由此证实了基于轨迹跟踪的线性时滞系统稳定性自动化控制方法是具有有效性的。

5 结语

时滞的存在会导致系统极其不稳定，因此对时滞系统稳定性研究是具有必要性的。研究的内容主要包括三个方面：

1）描述时滞问题所在，提出无记忆状态反馈矩阵和有记忆状态反馈矩阵。

2）分析时滞系统稳定性，并构建Lyapunow-Krasovskii泛函，获取最新不等式，得到时滞系统稳定判据。

3）根据系统稳定性依据，利用基于轨迹跟踪控制方法，得到保守性较高的系统控制条件。

根据实验结果可知，与传统方法相比，本文方法的控制效果更好，充分验证了该方法的有效性。

虽然本文方法较好的解决了传统方法存在的问题，但是在线性时滞系统的稳定性问题上需要进一步完善，有必要从以下三个方面探究：

1）在Lyapunow-Krasovskii泛函选取上，需构造泛函使问题变得更加简单，同时得到稳定性判据，这是需要继续解决的问题。

2）在不等式问题上，需利用更加先进技术推进不等式的计算，这也是未来需要努力的方向。

3）在控制领域中，单纯分析稳定性是不足的，需对系统进行严格控制，保证系统达到稳定状态。