拖曳系统变速拖曳的振动响应

王志博

（江苏科技大学，江苏 张家港 215600）

0 引 言

海洋拖曳系统通常在复杂的海洋环境中工作，其母船在海况多变的水面上航行时，在风、浪、流的作用下，有时难以维持恒定的航速和航向。受不稳定的航向和不断变化的拖曳速度的影响，拖曳系统会产生振动响应。拖曳系统由拖曳体、拖曳缆和母船组成，在拖航过程中可利用母船的加速运动使其迅速抬升，避免在抵近海底观测时与障碍物发生碰撞。通过提高拖曳系统的运行速度，不仅能快速提升拖曳体，减小其下潜深度，而且能在拖曳速度更快时使缆内的张力减小。

拖曳系统加速运动时，拖曳缆的张拉力迅速增大，对拖曳缆产生冲击作用，使拖曳系统发生振动。从能量的观点看，拖曳系统的加速运动使得其在较短的时间内产生了一定量的动能，作为柔性空间系统，为达到新的能量平衡状态，除了水流作用力耗散部分动能以外，需以振动的形式耗散剩余动能。然而，高张力的拖曳缆和拖曳体构成的拖曳结构是低阻尼的运动结构，由于阻尼水平较低，动能因拖曳缆的振动而扩散，最终被绕缆和拖曳体周围的流体吸收。

NIEDZWECKI等[1]建立海洋缆冲击张力的有限元模型，并通过冲击试验对其有效性进行验证，该模型对阻尼的近似估算较为粗略，不适于对拖曳缆空间弯曲的振动传递进行描述。HUANG等[2]和VASSALOS等[3]采用集中质量方法建立拖曳系统的计算模型，并将其应用于规则波激励下的拖曳系统的运动响应分析中。HENNESSEY等[4]开展缆绳的冲击张力试验，总结缆绳张力受冲击作用之后的快速振荡衰减的特征。PLAUT等[5]对系泊缆绳的冲击运动进行模拟和总结。WANG等[6]对水面操纵引起的拖曳运动响应进行系统的归纳比较，提出典型的非线性运动响应。王志博等[7]建立模拟悬吊拖曳体冲击张力的运动模型并进行求解，获得冲击张力的分布特征。唐友刚等[8]模拟系泊缆的冲击行为，建立离散有限元方法模拟缆绳的冲击作用。张素侠[9]和程楠[10]对不同张力水平下的冲击响应进行建模和计算，给出松弛型系泊缆的冲击响应规律。王志博等[11]和朱克强等[12]对拖曳缆在长周期的运动冲击作用下的运动进行模拟。李英辉等[13]将拖曳体的运动与缆绳的运动相耦合计算二者的运动情况，但针对冲击状态下的拖曳拖体的六自由度运动求解，采用该方法会出现数值困难。

然而，拖曳缆在受冲击作用时出现的张力现象与系泊状态是不同的。拖曳系统在加速阶段受到的冲击张力属于短时的张力振荡，对该现象的捕捉需具有较高的时间分辨率。本文采用自适应时间区分方法与有限差分格式相结合的方法求解ABLOW等[14]和WU等[15]建立的动力学模型，拖曳系统振动的响应频率必然与拖曳缆的放缆长度、动量输入水平、拖曳系统的初始拖曳速度和最终拖曳速度、缆型及拖体质量有关。对拖曳系统的加速运动过程进行模拟，着重对拖曳系统的振动响应频率和冲击特征进行分析。此外，为给拖曳系统前期设计参数的选取和应用工况的设计提供参考，对振动传递承担效应进行综合分析。

1 数值计算模型

拖曳缆的放缆长度通常较大，扭转刚度和弯曲结构刚度对拖曳缆运动的影响通常可忽略。本文将较长的缆看作截面为圆形的光滑柔性缆，不考虑缆的扭转结构刚度和局部弯曲刚度效应，以及拖曳系统的振动传递受到的这2种结构刚度的影响。建立水深方向为z轴负方向的全局坐标系O-xyz，在拖曳缆上截取微元ds，该微元受到重力、浮力、水流作用力、附加质量力和缆内张力等力的作用，ABLOW等[14]应用牛顿第二定律在随体坐标系O-tnb中建立缆元的受力平衡方程，进而利用欧拉变换关系将微元的受力平衡方程转换到全局坐标系O-xyz中，建立动力学模型，即

本文运用该模型计算拖曳系统加速运动过程中在冲击张力作用下的响应运动，利用盒式差分格式求解ABLOW等[14]给出的模型。空间结构矩阵的对角线系数为

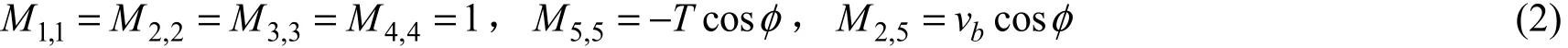
非对角线的非零系数为

时间相关系数矩阵的非零变量为

源项Q的非零项表示为

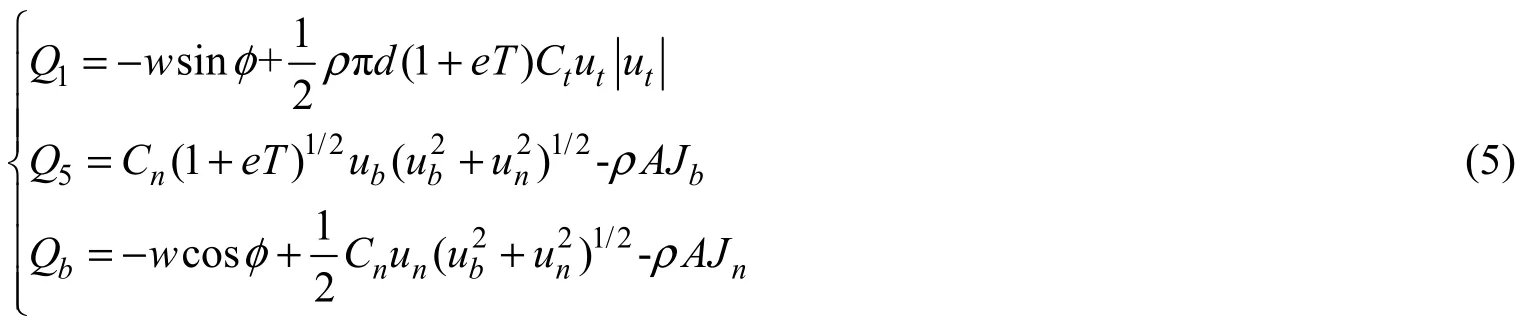
式(1)～式(5)中：w为单位缆长质量；ma为缆的附加质量系数；A为缆元迎流面积；e为缆受到的张拉应变量；k为缆的张拉模量；Cn和Ct为缆元受到的水流阻力系数；Jb和Jn为海流速度在缆元处的法向和切向分量。

未知变量为缆内张力T、缆的运动速度(vt,vn,vb)和相位角θ、φ。

观察结构矩阵可知，在加速运动的情况下，拖曳系统在张力的作用下出现振荡现象，导致该结构矩阵的性质发生一定的变化，振荡越小表示2次迭代值之间的变化越小。

根据牛顿第二定律将拖曳体简化为质点运动，有

质量系数矩阵表示为

式(6)～式(10)中：m为拖曳体质量；maX、maY和maz为拖曳体三向附加质量；LX、LY和LZ为拖曳体的三向特征长度；V为拖曳体排水体积；u为拖曳体运动速度。

本文以Burgess推导的盒式格式为基础，在每个时间步长内增加松弛因子，在时间步长内多次迭代计算满足求解精度要求，求解离散方程。

为避免每个时间步长内的张力求解值的差别较大造成数值求解不稳定，采用自适应时间步长的方法求解上述盒式差分格式。首先取时间步长为某个初始时间步长T0，令k=1。

若在该时间步长内计算收敛，则仍需令k增大，计算新时间步长对应的张力值与上一个时间步长对应的张力值的差别。通过不断增大k值，得到2个时间步内的张力值的差别满足相对误差ε＜0ε，即可认为达到对振动作用的时间分辨率。

本文利用HUANG等[2]给出的算例（见表1）进行验证，在该拖曳系统的基础上扩展进行加速运动的振动响应计算。拖曳缆水下端在O-xy水平面的运动轨迹与水深z向的升沉历程的计算结果对比见图1。通过比较可知，拖曳体的升沉运动与水平面内的运动轨迹基本一致，验证了该模型对应程序的正确性。

在HUANG等[2]给出的算例的基础上，为考查拖曳系统参数变化对不同加速度的响应，设计表1所示的拖曳系统结构参数的变化，改变拖曳缆的放缆长度和拖曳体的质量，设计表2所示的拖曳系统加速时间段和起止拖曳速度。

表1 拖曳系统结构参数

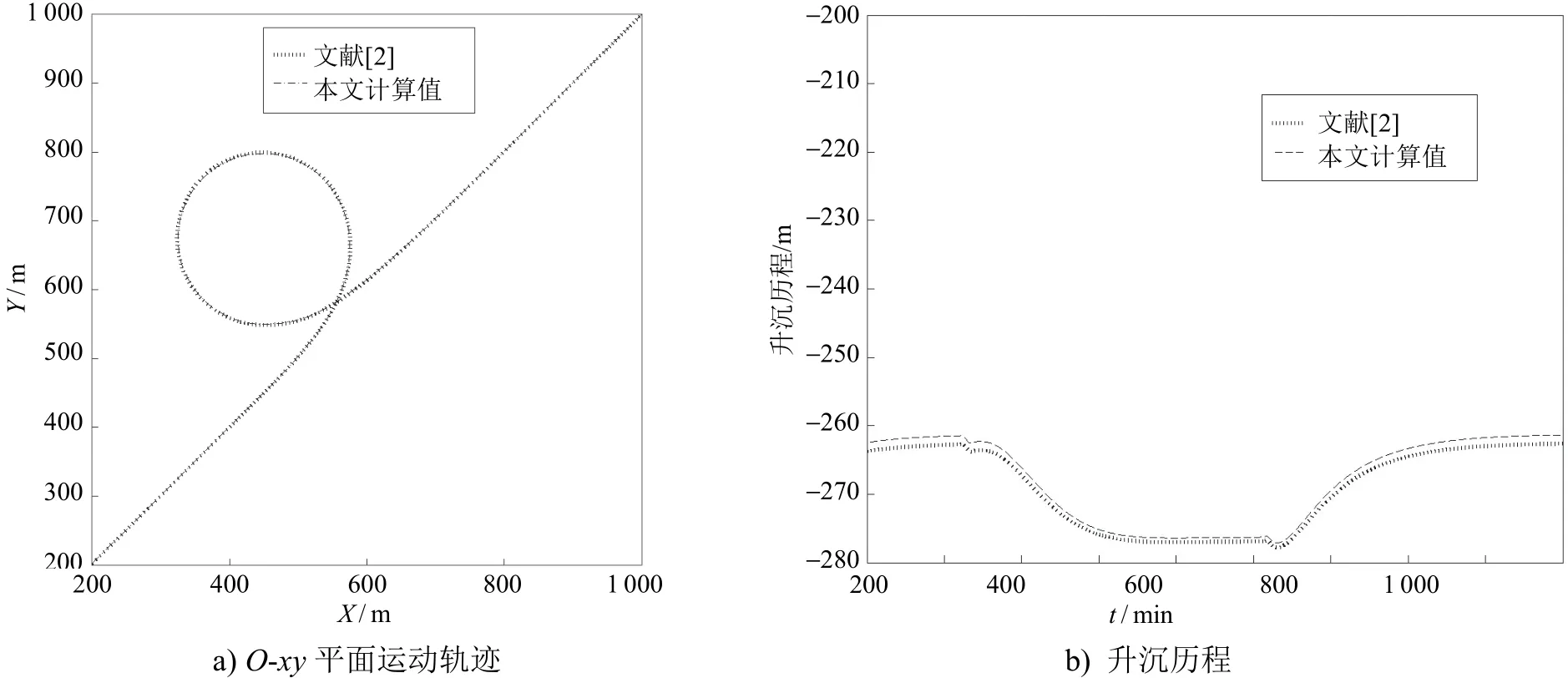
图1 文献[2]算例的计算验证

表2 拖曳系统加速时段与起止拖曳速度

2 加速运动与拖曳系统的结构参数的振动响应

2.1 设定加速时段与加速度，起始速度与终止速度不同的振动响应

拖曳系统在不同拖曳速度下的沉深和缆形不同，缆内的张力水平不同，因此在不同的初始速度下加速到一个较高的速度，必然会造成拖曳体沉深下降，缆内的张力下降。图2为拖曳体在不同加速阶段的升沉运动响应。加速阶段存在张力的2个振荡响应分别为初始阶段的振动响应和终止阶段的振荡响应，随着张力的不稳定变化，拖曳体的高度先增大后减小。

图3为拖曳系统进入加速阶段时的冲击张力的振荡情况。计算结果显示：在较小的拖曳速度下进入加速状态，拖曳缆内的冲击张力较小；随着初始拖曳速度的增大，拖曳缆内的张力冲击峰值增大，在几秒钟的时间内，缆内张力多次振荡，随后缓慢减小，对应于拖曳缆的空间缆型是缓慢爬升，拖曳系统在获得稳定的动能输入之后呈现出良好的线性行为。图4为终止阶段的拖曳缆的张力的振荡特征。尽管终止阶段速度不同，拖曳系统在动能输入停止之后的振荡显示冲击张力的峰值几乎没有变化，在短时间内经历了多个振荡衰减之后，拖曳缆内的张力趋于新的稳定值。

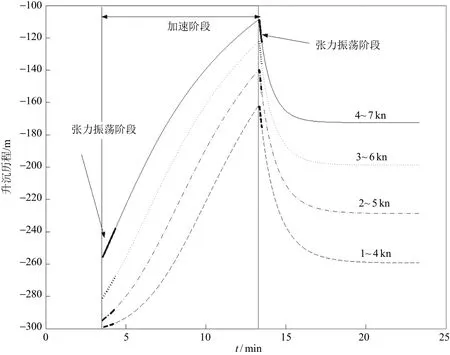
图2 加速阶段的拖曳体的升沉运动历程（缆长300m，拖曳体质量3000kg）

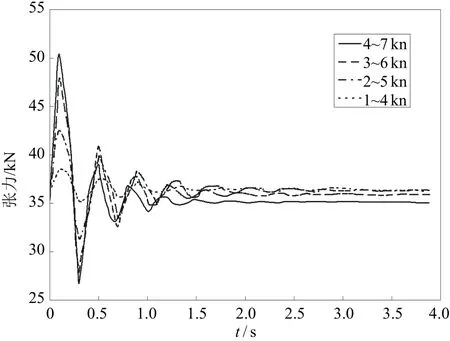
图3 初始加速阶段的缆振动张力历程（缆长300m，拖曳体质量3000kg，10min加速）

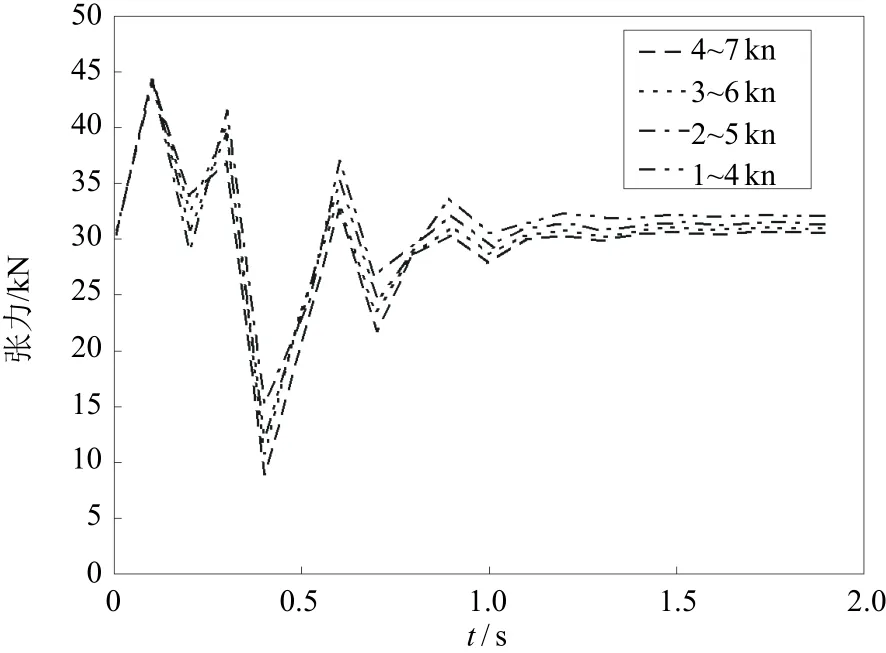
图4 终止加速阶段的缆振动张力历程（缆长300m，拖曳体质量3000kg，10min加速）

2.2 起始速度与终止速度相同的情况下不同加速时段和不同加速度振动响应

为分析拖曳系统受到的不同程度的加速作用对冲击张力的影响，设定起始速度为 2kn，终止速度为6kn，图5和图6为加速起始阶段和加速终止阶段拖曳缆内张力的振荡现象。由图5和图6可知：加速时间越短，拖曳系统受到的冲击作用越显著，拖曳缆的张力峰值越大，拖曳系统内的张力峰值随着拖曳缆的张拉作用越迅速衰减；随着拖曳缆的加速度减小，拖曳缆内的振动时间段增长。终止阶段的张力振荡显示出不同的振荡规律，在短时加速之后出现小张力阶段，随后又出现冲击峰值。这是由于拖曳缆加速结束之后，由于附加质量的作用，水流对冲击有阻滞作用。图 7为初始阶段和终止阶段的加速运动状态，随着加速时段的增长，冲击现象逐渐消失，更多地呈现出小张力的张力振荡现象。

图5 不同时间起始加速阶段的振动响应（缆长300m，拖曳体质量3000kg）

图6 不同时间终止加速阶段时的振动响应（缆长300m，拖曳体质量3000kg）

图7 张力振动的峰值 （缆长300m，拖曳体质量3000kg）

2.3 拖曳体质量对振动响应的影响

将拖曳体的质量调整为 400～1000kg，计算拖曳系统在相同初始速度、终止速度和加速时间段的运动响应。图8和图9为2个阶段的张力振动响应。随着拖曳体质量的增大，振荡冲击作用的张力峰值越大，但振荡持续的时间并未增加，加速结束之后张力峰值随着拖曳体质量的减小而增大，振荡冲击的时间段没有显著变化。加速结束阶段的张力峰值大于加速起始阶段的张力峰值。

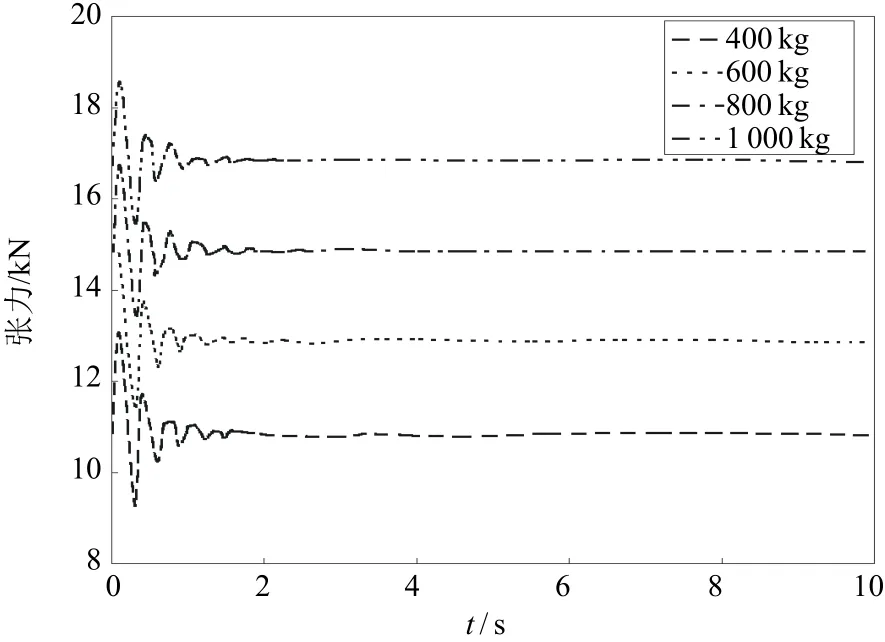
图8 加速起始阶段振动衰减（25min加速，缆长300m）

图9 加速结束阶段的振动衰减 （25min加速，缆长300m）

2.4 放缆缆长对冲击作用和频率的影响

可预见拖曳缆增长之后的弹性效应显著增大，对加速运动引起的2个阶段的张力振荡作用的持续时间增长。在由1kn加速到6kn的加速时段为25min的情况下，由于放缆长度增加，拖曳缆的张力峰值显著增大，振荡幅度和冲击效应显著增强（见图10和图11）。

图10 不同放缆长度对初始加速阶段的振动响应（25min加速，拖曳体质量3000kg）

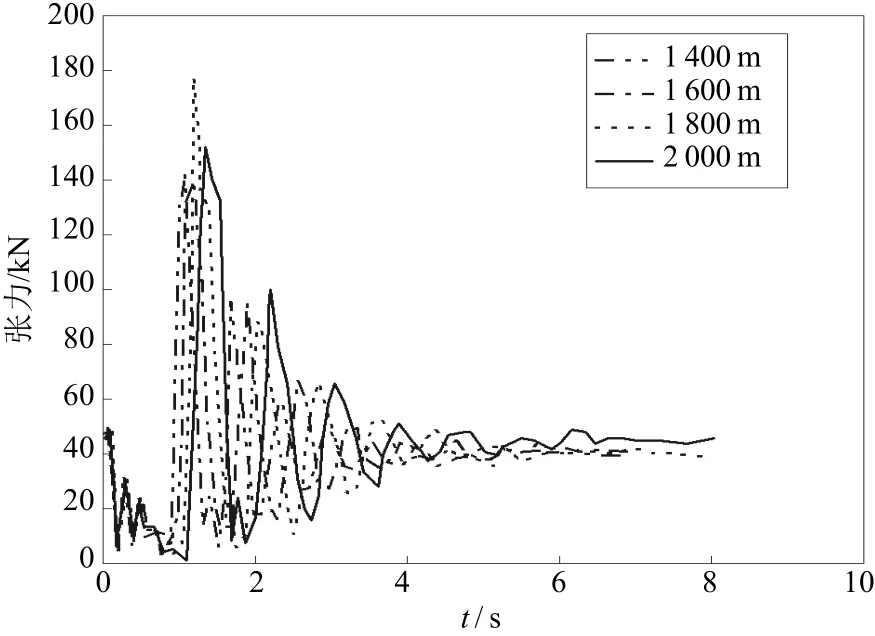
图11 不同放缆长度对加速终止阶段的振动响应（25min加速, 拖曳体质量3000kg）

3 结 语

本文通过建立自适应数值时间分辨方法，准确地模拟了拖曳系统受到加速运动激励而发生的短时振动现象。通过对拖曳系统在直航拖曳情况下进入加速阶段之后的2段短时振荡激励作用进行分析发现：

1) 加速过程中拖曳缆内的张力振荡先增大，后缓慢减小，对应于拖曳缆的空间缆型是缓慢爬升，拖曳系统在获得稳定的动能输入之后呈现出良好的线性行为。终止阶段对应的张力历程是张力陡降，随后出现冲击作用，冲击张力显著大于起始阶段的张力。

2) 拖曳体质量增大，振荡冲击作用显示的峰值增大，振荡持续的时间不随拖体质量发生变化，加速终止阶段的峰值随着拖曳体质量的减小而增大。

3) 加速时间越短，2个阶段的冲击作用越显著；加速时间越长，张力振荡的时间越长。

4) 放缆长度增大，拖曳系统的冲击效应显著增强。