某节制闸水流流动特性数值模拟研究

吕晓波 李太民 唐 波 施 翔

（1.江苏省骆运水利工程管理处 江苏宿迁 223800；2.宿迁市水务勘测设计研究有限公司 江苏宿迁 223800）

1 工程概况

节制闸按排洪50年一遇设计，100年一遇校核，设计校核排洪流量1 000 m3/s，建成后将全面提升其所在河段的防洪、排涝、灌溉、发电等综合功能。节制闸共7孔，每孔净宽10.0 m，闸孔总净宽70.0 m，闸底板宽20.0 m，底板面高程8.5 m，底板上设新型圆角梯形堰，堰顶高程11.5 m，上游堰高3.0 m，配弧形钢闸门和绳鼓启闭机进行闸孔泄流控制；闸墩中墩厚1.2 m，边墩厚1.0 m，闸墩顶高程20.0 m；节制闸一侧设2孔3.0 m净宽小水电孔，设2台机组，每台容量160 kW。节制闸上游设35.0 m宽钢筋砼护坦，护坦面高程8.5～12.0 m；节制闸下游消力池长40.0 m，池深2.0 m，池面高程6.0 m；海漫长50.0 m，面高程为6.5～7.5 m，纵坡为3%；抛石防冲槽深3.5 m，面高程6.5 m。

2 节制闸三维水流数值模拟

随着计算机技术的飞速发展及水动力学计算方法的进步，对水流问题进行数值模拟研究已被广泛运用于水利工程。近年来，计算流体力学的广泛应用，涌现出不少数值计算软件，如Flow-3D、Fluent等，其中Flow-3D对水流自由表面有较精确的追踪优势。本文采用Flow-3D软件对节制闸水流流动特性进行数值模拟研究。

2.1 数值模拟基本理论

对流体进行数值模拟的实质就是将连续流体用离散方式在计算机上进行处理，即将时间和空间上都连续的物理量的场对应成有限多个离散点，建立起一定规则的变量方程，进行求解。通过调整变量，计算出其他物理量，从而得到流体各相关量的关系。

2.1.1 控制方程

采用完整的纳维-斯托克斯方程[1]（Navier-Stokes equation）作为控制方程:

式中:U=（u，v，w）为流速；ρ为压力；G 为重力和非惯性力；Τ 为应力张量；K（u，v，w）为拽力；RSOR/ρ为因质量注入产生的加速度；F为表面张力等合外力。

2.1.2 紊流模型

流体数值计算需选择合适的紊流模型。紊流的数值模拟通常有直接数值模拟、大涡数值模拟和雷诺时均模拟三种。本文研究对象为过闸水流的紊流流动，涉及螺旋流和孔流，部分区域流线不规则，水面形态复杂。RNG k-ε紊流模型比标准k-ε紊流模型能更好地处理高应变率及流线较大弯曲的流动[2]，故采用RNG k-ε模型运用雷诺时均算法对过闸水流进行数值模拟。

RNG k-ε模型[3]由Yakhot和Orzag于1986年研究提出，其方程形式如下所示:

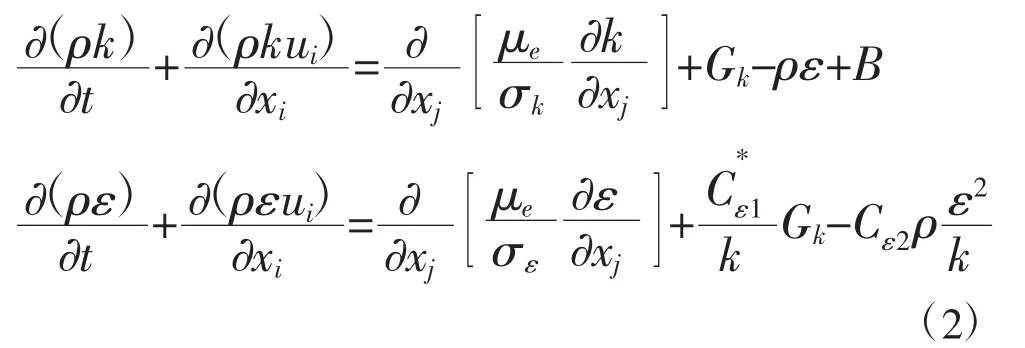
式中:xi，xj为空间坐标位置；ui为时均流速分量；B为体积力项；p为时均压强；μ为分子动力粘性系数；ρ为流体密度；μe为分子有效动力粘性系数；Gk为产生项。

方程中的系数分别为:

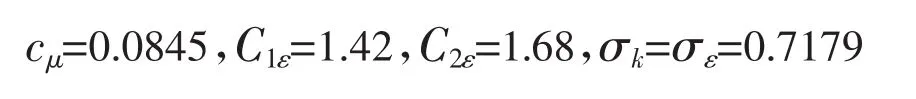
2.1.3 自由表面模拟

水利工程中大部分水流均带有自由液面，对自由表面的模拟是数值模拟的难题之一。国内外有关专家针对此问题做出了各种研究，提出了多种处理方法，如 VOF 法[4]、刚盖假定法[5]、标高函数法[6]、MAC 法[7]等。本文采用Flow-3D中VOF法模拟自由水面。

VOF法由Dr.Hirt和Dr.Nichols于1975年发表提出，VOF法的原理是利用流体占据网格单元的体积比值函数来追踪自由面的变化。这种方法不仅能追踪流体表面上的质点，还能追踪流体表面的变化。VOF法中定义了一个函数F，表示流体的体积分数，即单元网格内流体体积与网格体积的比值，且每个单元体中只存在一个F函数。

F函数满足如下方程:

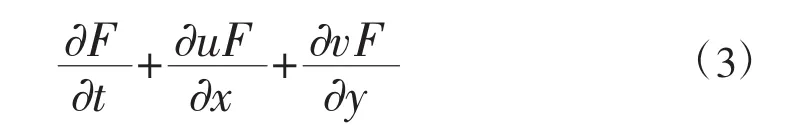
由上式可得各单元体中的流体体积分数F，从而追踪出自由表面的位置。若F=1，表示整个单元体中完全充满了流体；若0＜F＜1，表示单元体中含有流体和气体等其他相的物质，即流体未完全充满单元体；若F=0，则表示单元体中没有流体。

2.1.4 边界条件的设定

边界条件的选择和设定是CFD数值模拟的重要组成部分，边界条件给定模型边界处的变量以及该变量随时间或空间的变化规律。常见的边界条件有压力、速度、对称、自由出流、壁面等边界条件。

本文针对过闸水流流态，选择了速度、压力、壁面和自由出流四种边界条件。在压力进口设置中设定上游水深，出口设置为一定水深的自由出流。

2.2 节制闸三维模型建立

三维模型以某节制闸工程为原型，采用CAD绘图软件按1∶1比尺建立，然后导入Flow-3D软件进行数值模拟，三维模型如图1所示。模拟范围为闸前后长度共400.0 m，上游204.0 m，下游196.0 m，涵盖主要研究区域。

网格划分采用Flow-3D中FAVOR技术，用矩形网格描述曲面模型，模拟的准确性较高。FAVOR利用线性差分来刻画模型面积，能自由捕捉模型表面，用较少的网格模拟复杂问题。因节制闸附近水流流态变化较大，为准确模拟水流流态及捕捉水面线，在节制闸附近采用网格局部加密技术。节制闸三维模型共剖分1 574 727个网格，网格接近立方体，均匀有序排列，划分网格后的三维有限元模型如图2所示。

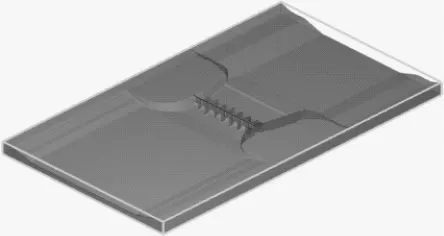
图1 节制闸三维模型结构图

图2 闸的三维水流模型网格剖分示意图

2.3 模拟结果及分析

2.3.1 电站不运行各工况上下游水面线

根据节制闸运行情况，电站不过流7孔闸门均匀开启，校核工况下，上游水位17.5 m，下游水位17.0 m，泄洪闸通过1000.0m3/s流量，闸门开启高度为4.88 m；设计工况下，上游水位17.0 m，下游水位16.5 m，泄洪闸通过1 000.0 m3/s流量，闸门开启高度为4.79 m。计算工况表如表1所示。

表1 节制闸运行计算工况表（电站不运行）

校核及设计工况下上下游水面线如图3、图4所示。

图3 校核工况节制闸上下游水面线

图4 设计工况节制闸上下游水面线

由图3、图4可知，校核及设计工况下，上游水位相对稳定，水面线无明显变化。因下游水位较高，出闸水流为淹没出流，消力池内水位有所降低，出消力池后水位逐渐恢复。

2.3.2 电站不运行各工况上下游水流流速分布

电站不运行各运行工况节制闸上下游水流流速分布如图5、图6所示。

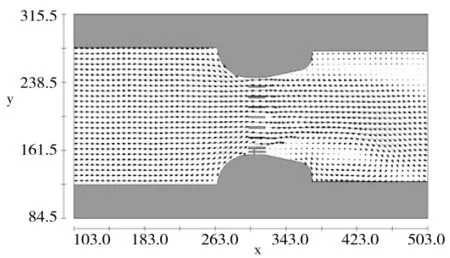
图5 校核工况节制闸上下游水流流速分布

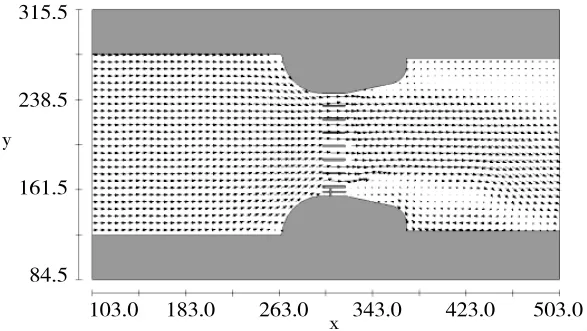
图6 设计工况节制闸上下游水流流速分布

由图5、图6可知，校核及设计工况下，上游来流平顺，水流流速分布均匀。因电站进水口不过流，主流略偏向左侧，下游消力池及下游渠道右侧有低流速回流区存在。

2.3.3 电站运行各工况计算

为研究电站运行时节制闸过流及闸后水流流态，增加计算电站运行工况，各工况下水流物理参数如表2所示。

表2 节制闸运行工况表（电站运行）

各工况下节制闸上下游水流流速分布如图7、图8所示。

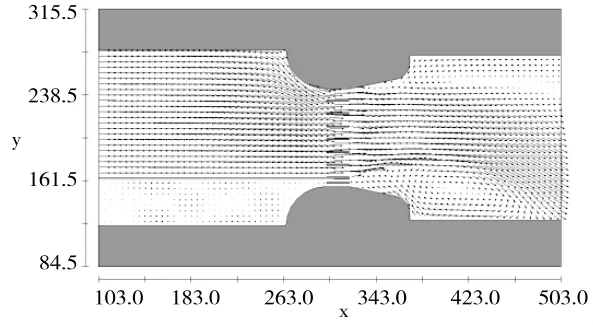
图7 校核工况节制闸上下游水流流速分布

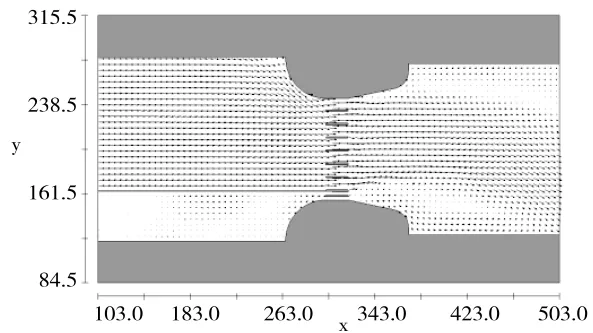
图8 设计工况节制闸上下游水流流速分布

由图7、图8可知，校核及设计工况，电站过流情况下，上游来流平顺，水流流速分布均匀。因电站侧流量仅有10.0 m3/s，主流略偏向左侧，下游消力池及下游渠道右侧依然有低流速回流区存在。上游侧电站侧低流速区存在是因确定水闸与电站分流比而采取分区处理的原因，上游侧流速分布与真实情况有所差异，但并不会影响下游流速分布。

2.3.4 闸门开启运行方式计算

节制闸开启泄流时，为避免闸下水流出现偏流、回流及折冲水流等不良流态，节制闸各闸孔开启方式一般为同步均匀开启或对称开启。为研究电站运行时，闸门不同开启方式对水闸过流及闸后水流流态的影响，进行了闸门运行开启方式的计算比较，为便于比较，闸下计算水位选取设计工况的16.5 m，并采用相同流量进行研究，计算工况见表3，计算结果如图9、图10、图11 所示。

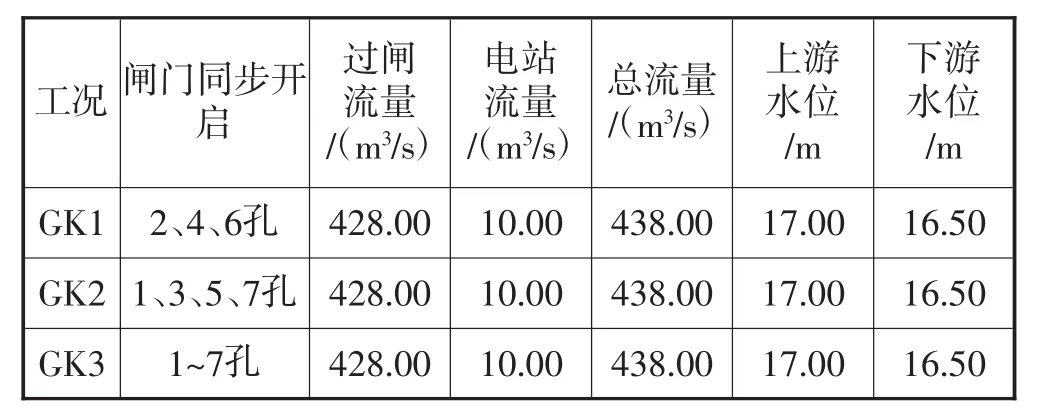
表3 闸门开启运行方式计算工况表

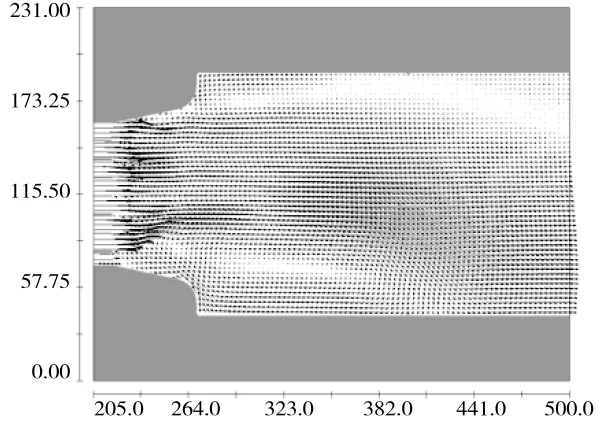
图9 工况GK1节制闸下游水流流速分布

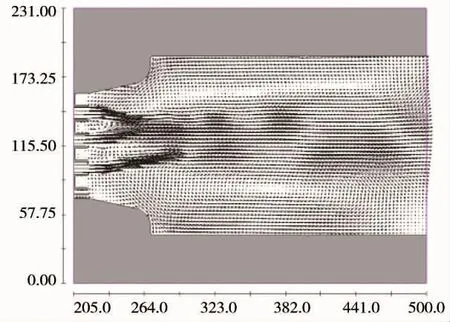
图10 工况GK2节制闸下游水流流速分布

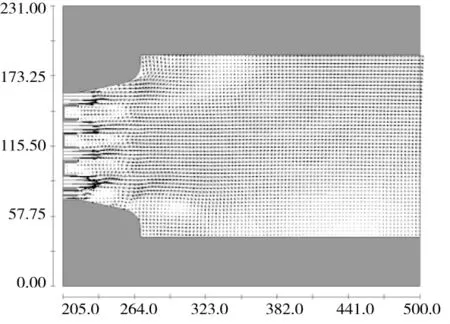
图11 工况GK3节制闸下游水流流速分布

由图9～图11可知，在上下游水位一致、过闸流量相同、电站过流情况下，不同的闸门运行方式，节制闸下游流速分布规律并不相同。当节制闸2、4、6孔同步开启时，因主流集中于节制闸下游河道中部，两侧均出现明显回流区；当节制闸1、3、5、7孔同步开启时，节制闸下游流速分布相对均匀，因受电站侧过流的影响，节制闸下游右侧出现较小范围回流区；当节制闸1～7孔同步均匀开启时，节制闸下游右侧出现较大范围回流区。分析其原因，首先因受电站侧过流的影响；其次节制闸下泄相同流量下，靠近电站侧闸孔出流水体动量小于其它工况，主流受电站侧回流区挤压较强。

3 结语

本文基于三维水流数学模型，运用Flow-3D软件，选取RNG k-ε紊流模型和VOF法模拟了节制闸不同泄流方式闸下水流的流动规律；得出电站不同运行工况节制闸上下游水面线、水流流速分布，闸门不同开启方式闸下游水流流速分布。数值模拟结果可为节制闸的运行管理及优化调度提供科学依据。