基于多信息素蚁群算法的联合任务分配方法

魏得路，张雪松，胡 明

(1.电子科技大学，四川 成都 611731； 2.中国电子科学研究院，北京 100041)

0 引 言

舰载航空兵作为航母编队攻防作战的核心力量，预警机、战斗机、电子战飞机、反潜机、无人机、勤务机等多机种联合执行作战任务是航母编队的基本作战样式。要使得联合作战发挥最大效能，必须合理的分配任务，使得各作战平台在合适的地点和时间去执行合适的任务。任务分配问题的模型主要有车辆路径问题模型、动态网络流优化模型、多旅行商问题模型等，它是一个NP完全问题。对于此类问题，精确算法大多难以求解，因此多采用近似算法，如贪心法和启发式算法等。其中贪心算法主要有动态列表规划(Dynamic List Scheduling，DLS)算法[1-2]，以及基于DLS改进的MPDLS算法等。文献[3]将布谷鸟搜索算法与MPDLS算法结合，以任务完成时间以及资源利用率为优化目标求解了任务的分配。启发式算法有禁忌搜索、模拟退火等搜索算法[4]，以及遗传算法、蚁群算法、粒子群算法等群体智能算法。文献[5]将导弹群对多目标的问题建模，采用遗传算法求解。文献[6]将多无人机任务分配问题建模为多旅行商问题模型，并采用蚁群算法求解。

然而，当前对于任务分配的研究，还存在几个问题。首先，大多数研究忽略了作战半径的影响。在作战半径与战场尺度相比较小情况下，作战半径对距离的影响不大，但对于预警机及某些无人侦察机来说，其作战半径较大，不可忽略。第二个问题是大多数研究没有考虑多机种联合任务的分配，对联合任务分配没有提出有效的解决方案[7]。针对以上两点，本文将分配问题建模为复杂的多旅行商问题，以图中边的组合作为分配问题的解，改进蚁群算法为多信息素蚁群算法，通过蚁群的学习对图进行剪枝搜索，为任务分配问题提供了一个有效的解决方案。

1 联合任务分配问题模型

1.1 基本描述

飞行平台与联合任务的描述为：

(1)联合任务是作战的目标，其相应的属性有：任务Ti,i=1,2,3…N的位置坐标Positioni=(xi,yi)；任务Ti需要的执行时间tdi；任务Ti需要的平台的类型和数量矢量bi=(bi1,bi2,bi3,…bim)，其中bim表示任务Ti需要的类型为m的平台的数量。

(2)飞行平台是任务的执行者，它的属性有：平台Pi,i=1,2,3…M的类型tpi；平台Pi的位置Positioni=(xi,yi)；平台Pi的移动速度vi；平台的作战半径Ri。

任务的执行矩阵代表着平台与任务的匹配关系。对于m个平台，n个任务的任务分配问题，执行矩阵是一个mn的矩阵。如式(1)中矩阵E表示一个执行矩阵，其中xij=1代表平台Pi参与执行任务Tj，否则代表平台Pi不参与执行任务Tj。根据该矩阵的第i行可得到平台Pi参与的所有任务；相应的，根据矩阵第j行，可得到参与Tj的所有平台。

(1)

1.2 平台的路线模型

联合任务分配中，存在平台参与多个任务的情况，这就要求计算出平台抵达每个任务的时间。各类型舰载机作战半径各不相同，轰炸机、战斗机等需要在任务点几公里内进行作战，而预警机侦察机等甚至可以在一百甚至几百公里外参战。在估算平台执行任务的航程时，需要考虑到平台的作战半径。目前大多数对于任务分配的研究都忽略了作战半径的影响，直接使用平台和任务之间的距离当作平台参与任务需要飞行的距离，导致估算时与实际情况相差较多。

考虑到作战半径对平台执行任务的影响，以及以下两个因素：(1)平台最快到达可执行任务点；(2)充分利用平台在任务区内等待其他协作平台到位的空闲时间。本文提出了一种新的平台移动方式，如图1，平台当前将要执行的任务为任务1，平台的接下来一个任务为任务2，并且定义平台飞行中两个关键位置：(1)任务进入点，即平台进入任务区的位置；(2)任务执行点即平台执行任务的位置。则平台的移动方式为：

(1)对于任务1，平台的移动方式为从当前位置到任务位置直线移动，保证最快的时间到达任务区，直到平台与任务之间距离小于或等于平台作战半径，这时平台所处位置为任务进入点(图1(a)中a点)；

(2)此时平台已经可以开始执行任务，但可能处于等待其他平台就位状态中，此时平台移动目标为当前任务区中离任务2最近点(图1(b)中b点)；

(3)移动过程中，若其他参与平台已就位，则任务1开始执行，这时的位置为平台的任务1执行点(图1(c)中c点)；

(4)任务1执行完毕后，平台开始向下一个任务移动，目标为任务2的任务区进入点(图1(c)中d点)，移动方式与任务1移动方式相同。

图1 平台移动方式

通过这种方式，充分利用了平台等待的时间，将平台参与的所有任务的路线以迭代的方式计算出来，所有平台共同迭代可以求得所有任务的开始执行时间以及完成所有任务的时间，为后续航线规划提供更精确的支持。

下面分析这种航程估算方式与传统方式的差别。如图2所示，两种估算方式的对应的航程分别为a-c-d和a-O1-e，其中c的位置为线段ab上一点。若平台进入任务1的路线与任务2的夹角为θ，平台作战半径为R，任务之间距离为d，当c点位于a和b时，两段航程之间的距离差的最大值和最小值分别如公式(2)和(3)所示。

(2)

(3)

随着夹角θ在(0-180)之间不断增加，航程距离差逐渐减少。θ为180时，航程差为0，而θ为0时，航程差为最大值2R。

随着作战半径的增加，航程差逐渐增加。公式(2)和(3)证明，随着作战半径的增加，传统的忽略作战半径的航程估算误差值越来越大。

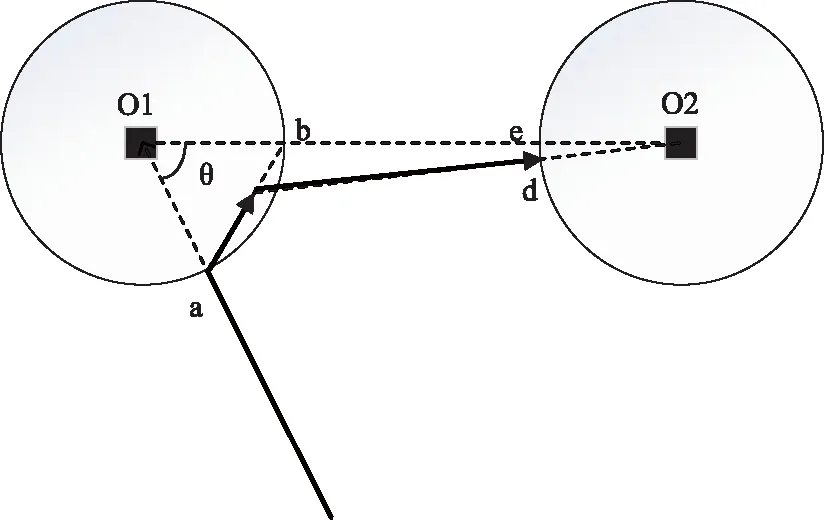
图2 航程比较示意图

1.3 任务分配问题数学模型

联合任务分配的问题可以描述为：对于若干平台和任务的场景，找到或调整任务的分配顺序和任务的执行矩阵，在满足平台的参数、任务的要求等约束条件下，达到最优化目标。本文重点研究平台在空间上的移动与协作，以最小化任务完成时间为目标，将联合任务分配问题的约束条件和目标函数定义为：

约束条件：

(1)任务完成约束。对于每一个任务，根据任务需求的平台类型和相应的数量，选择参与该任务的平台，选中的数量不少于任务需求。

(2)平台可达性约束。平台在执行任务时，要在任务执行时间之前抵达任务区。

目标函数：完成所有任务花费的时间最短。

本文以MTSP模型为基础，将平台和任务看作旅行商和城市，将任务之间的迁移代价看作城市之间的距离，将任务的分配看作城市的访问，将联合任务预分配问题描述为协作多旅行商问题(Collaborative Multiple Salesman Problem，CMTSP)模型：存在若干旅行商和一定个数的城市，其中旅行商分为几个类型，每个城市需要一定个数的各种类型的旅行商一起表演一段时间，寻找旅行商在所有城市表演完成的最短时间以及访问方案。将该问题表示成图问题，旅行商对应图中的节点，城市之间的路线对应图中的边，问题的解为图中某些边的组合，这样就把联合任务分配问题表示成了一个图问题。

其数学描述如公式(4)所示。其中(t1,t2,…tn)代表各个任务的完成时间，bij和numij分别代表第i个任务需要的第j类飞机数量和参与该任务的数量，公式约束条件中第一部分表示对于每个任务，参与执行任务的平台数量不少于任务需求的数量。公式中frt(i,j)表示平台Pi到达j任务的时间，由任务之间的航程与平台速度相除得到，其中航程按照本章第四小节的方法来进行计算。task(m,k)表示平台Pm任务列表中执行的第k个任务的编号，tdj为编号j的任务需要的执行时间，则tj-tdj为该任务的开始执行时间。约束条件第二部分表示，对于每个平台，平台抵达须执行任务的时间不晚于任务开始时间。

min max(t1,t2,…tn)

(4)

2 多信息素蚁群算法

联合任务分配问题是NP问题，在规模较大时难以用精确算法求解。某些贪心算法如合同网算法中并不能找到完美的任务排序与平台选择策略，且没有对结果的反馈以学习更优的选择策略。启发式算法中，遗传算法并不能很好的利用一些现有规则，而蚁群算法天然的带有启发函数这个概念，可以更好地利用经验知识，同时使用信息素修补经验知识的不足。因此，本文以合同网的思路改进蚁群算法，对联合任务分配问题进行求解，如图3所示。其中任务排序策略和平台选择策略都使用启发函数和信息素结合的方式，终止条件定义为到达最大迭代次数或者算法已经收敛，反馈通过对信息素进行调整来实现。

图3 问题求解思路图

2.1 基本蚁群算法

M.Dorigo根据蚂蚁在寻找食物中的行为，发现蚂蚁可以在协作的情况下发现觅食的较短路线。经过研究发现，蚂蚁在移动的过程中会释放一种称为信息素(pheromone)的物质。蚁群之间通过信息素进行沟通，信息素越多的地方蚂蚁也会倾向于向那个方向移动。若在蚂蚁与食物之间有几条路线可以选择，刚开始的时候，所有路上都没有信息素，蚂蚁会随机移动。而随着蚂蚁的不断移动，较短路线上走过的蚂蚁数量较多，也会留下更多的信息素吸引其他蚂蚁过去，使得最短路线上的蚂蚁数量越来越多。

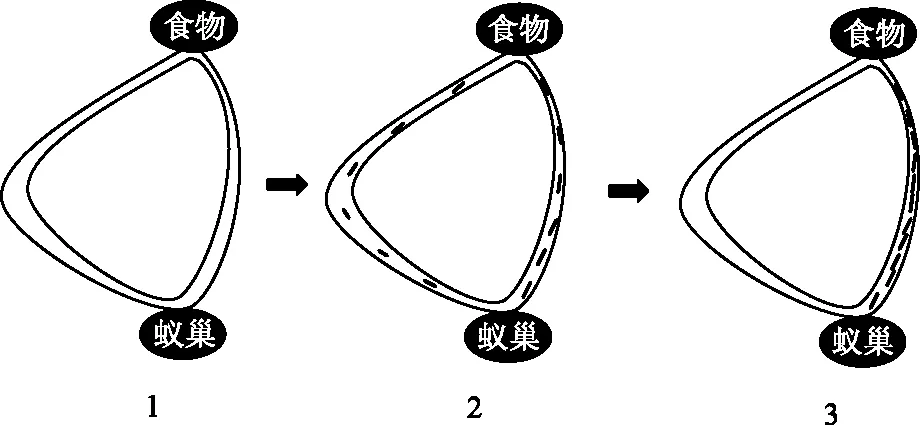
图4 蚁群寻路示意图

如图4所示，在蚂蚁搜寻食物过程中，没有信息素的时候蚂蚁随机选择路线，当某条路径较短，蚂蚁在此条路径上来回移动的次数较多，因此该条路径上留下的信息素会逐渐增加，而信息素的积累也会诱使蚂蚁选择该条路径，这样就形成了一个正反馈。最终，大多数蚂蚁选择的哪条路线很可能就是觅食的最短路线。当然，信息素不是一成不变的，它还有挥发性。蚂蚁并不完全根据信息素的含量来选择路线。大多数的蚂蚁倾向于选择信息素含量高的路线，也有少数蚂蚁会随机选择路线，若有蚂蚁找到了更短的路线，则更短路线上信息素会逐渐增加，原路线上的信息素逐渐挥发，新的更短路线会成为大多数蚂蚁的选择。

(5)

某些无效路径上的信息素需要进行调整，以防止其吸引其他蚂蚁。若在t+n时刻所有蚂蚁移动完成，则t+n时刻对路径Lij上的信息量按公式(6)进行调整。

(6)

公式(6)中p表示信息素的挥发因子，表示信息素在该次更新中先衰减为原来的1-p倍。在算法中，p的值很重要，会影响到算法的收敛速度。若p的值过大，则信息素难以积累，算法随机性过大，算法容易波动，难以收敛；若p的值过小，则算法收敛速度太快，容易收敛到局部最优解，难以进行大范围的搜索。公式(6)中的δij(k,t)表示编号k的蚂蚁在i城市与j城市之间移动增加的信息素。

算法中蚂蚁不断地移动，最终信息素收敛到目标路线上，也就对原问题做出了求解。

2.2 算法改进策略

2.2.1多信息素

多信息素蚁群算法采用城市被访问的时间作为基础构造启发函数，算法中的蚂蚁移动由蚁群算法中的单个蚂蚁移动变为一组的多个蚂蚁的共同移动，算法中的信息素更新则是各蚂蚁更新对应的那一种信息素。

一个经典案例为：飞行平台的数量为m，任务数量为n，平台类别数为t，每一个种类的平台个数分别为(a1,a2,…at)，Pik表示类别为i的第k个平台，任务Tj需要的各类型平台数量分别为(bj1,bj2,…bjt)。下面依次案例介绍算法中的启发函数、蚂蚁的移动以及信息素的更新等。

2.2.2启发函数

启发函数是多信息素蚁群算法中重要的一部分，它作为一种“经验知识”，引导算法进化的方向，影响算法的效果。好的启发函数引导算法搜索适当的区域，让算法在更短的时间内获得较好的效果。蚁群算法求解TSP中，大多使用城市间距离的倒数作为启发函数，即离当前访问城市更近的城市，其启发函数的值越大，在信息素相同的情况下，被访问的概率也越大。在CMTSP中，城市和旅行商之间存在双向选择，选择下一个城市时要多个旅行商共同选择，选择去往该城市的旅行商时也需要一起选择。也就是说，求解CMTSP的多信息素蚁群算法需要有两个启发函数，一个选择城市，一个选择去往该城市的旅行商。

在这里，本文以飞行平台可以抵达任务区的时间为基础构造启发函数。公式(7)中frt(ik,j)表示平台Pik到达任务Tj任务区的时间，x和y代表相应的平台或任务的位置坐标，Rik代表平台的作战半径。公式8中RTij表示类别为i的飞机可抵达任务j的任务区的最小时间，fnmax(k,l)表示序列l中第k大的值，bji为任务Tj需要的类别为i的平台的数量。公式(9)表示任务Tj可被执行的最早时间的倒数作为启发函数Q(j)，其中Δ为修正因子，防止时间为0使得启发函数无穷大。

(7)

RTij=fnmax(bji,(frt(i1,j),frt(i2,j),…frt(iai,j))

(8)

(9)

因此，任务选取的启发函数可以描述为：该任务在当前状态下可最早被执行时间的倒数。若任务可在较短的时间内完成，即平台参与该任务的代价较低，则该任务的启发值较大，会更优先的被选择执行。

任务选取平台的启发函数也是根据平台抵达当前任务的时间得到。若当前选中任务为Tj，则平台Pik参与Tj的启发函数Q1(i,k,j)如公式(10)所示，其值为平台到达该任务区的时间的倒数，Δ为修正因子。

(10)

2.2.3蚂蚁移动

蚂蚁的移动是蚁群算法核心的一环，蚂蚁根据信息素和经验知识的引导移动的过程也是一个解的组合构造过程，因此这一步骤与问题本身性质有着紧密的结合。基本蚁群算法求解TSP时蚂蚁的移动指单个蚂蚁根据禁忌表在城市之间移动，直到走完所有的城市，构造出TSP的一个解。多信息素蚁群算法中蚂蚁的移动代表的是一组蚂蚁的共同移动。对于m个旅行商和n个城市的CMTSP，算法使用m只蚂蚁代表m个旅行商，用蚂蚁的移动代表旅行商访问城市。蚂蚁移动的过程主要步骤为：

Step1：初始化已访问城市列表；

Step2：从未访问的城市选择一个作为下一个将要访问的目标；

Step3：根据城市的需要，选择几个蚂蚁访问该选中的城市。若找不到满足条件的蚂蚁，则蚂蚁移动结束，且没有获得一个可行解；

Step4：确定这几只蚂蚁共同的访问时间，更新这几只蚂蚁的状态；

Step5：更新城市状态为已访问；

Step6：若所有城市访问已完成，则蚂蚁的移动结束，获得一个移动方式，否则转Step2；

(11)

(12)

式(11)中综合m种信息素，依据信息素对应的平台的类别，对信息素分类处理。式(12)中α、β分别为信息素和启发函数重要性因子，α的值越大则信息素的影响越大，算法的搜索空间更大；β值越大，表示启发函数的影响越大，算法的搜索更精细致。

若编号k的城市被选中，接下来要选择去往k的蚂蚁。Step3根据城市k需要的旅行商的种类，同样采取赌轮盘的方式，从每个种类的蚂蚁中抽取该种类所需数量的蚂蚁去往该城市。以第i类为例，该种类共有ai个蚂蚁，当前城市k需要第i类蚂蚁数量为bki，则赌轮盘目的为从ai个蚂蚁中抽取bki个，已经被选中的蚂蚁会从allowed表中移除，保证不会重复抽取。抽取的依据也是信息素含量和启发函数，第i类编号x的蚂蚁每轮被选中的概率如公式(13)所示。

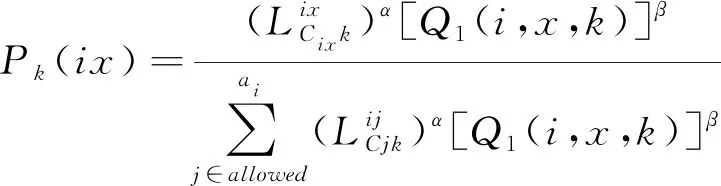
(13)

抽取完成后，综合所有蚂蚁的抵达时间，确定所有选中蚂蚁访问的最终时间，更新选中蚂蚁的状态，继续选择下一个城市直到所有城市访问完毕。

2.2.4信息素更新

信息素是蚁群算法中蚂蚁对问题信息不停的试探中学习到的知识，同时指引着蚁群的动作，影响着算法的搜索方向和收敛结果。为了防止信息素残留在无效路径，对当前的信息素进行挥发操作，即当前所有信息素按一定比例减少。之后，根据各组蚂蚁解得质量情况，计算各组蚂蚁的适应度，进行信息素的增加。

在多信息素蚁群算法中，为了精确的描述问题，增加了多种信息素，信息素组合的种类更多，算法更容易进入局部最优解，因此采用少数精英更新和更新次数控制两种策略，其中将当前全局最优解作为精英的一个。

少数精英更新策略指只有种群中适应度较高的一部分参与信息素的更新，精英不仅包含最优解，还包含次优解。这种策略与上述的最优解更新类似，与最优解更新相比，既保留了较好个体的信息，又淘汰了较差的个体，兼顾了搜索速度与效果。

更新次数控制策略指每段信息素在每次迭代中可以更新的次数不超过某个值。这个策略旨在减缓算法收敛速度，增加算法的搜索空间。同时可更新次数采取变化的数值，算法初期为了全局搜索并避免过早收敛，将该值设置的较小；算法后期增加该值进行局部空间的搜索。

每组蚂蚁更新信息素增加量根据该组蚂蚁的适应度来计算。本文中使用种群中所有组蚂蚁游历完所有城市后的时间计算各组蚂蚁应更新的信息素含量，若各组蚂蚁游历时间最大值为tmax，最小值为tmin，若某组蚂蚁遍历的时间为t，则该组增加的信息素如公式(14)所示。

(14)

式(14)中μ为每次更新最多的信息量，w为权重参数，值越大则该组蚂蚁更新的信息素与最大值差距越大，该组蚂蚁的路线越容易被淘汰。每组蚂蚁增加信息素时，只增加本组内蚂蚁经过的路线的信息素。

信息素更新的步骤主要有：

Step1：初始化所有种类信息素每段上的已更新次数；

Step2：计算各组蚂蚁的适应度和信息素更新量；

Step3：场上信息素按照信息素挥发速率进行衰减；

Step4：将所有组蚂蚁的信息素更新量进行排序，选取前v组作为精英；

Step5：选中的v组蚂蚁按照更新量依次增加信息素，若某种信息素在某段更新次数达到最大更新次数则跳过这段的信息素的更新。

2.3 算法步骤

算法流程图如图5所示，算法的整体步骤为：

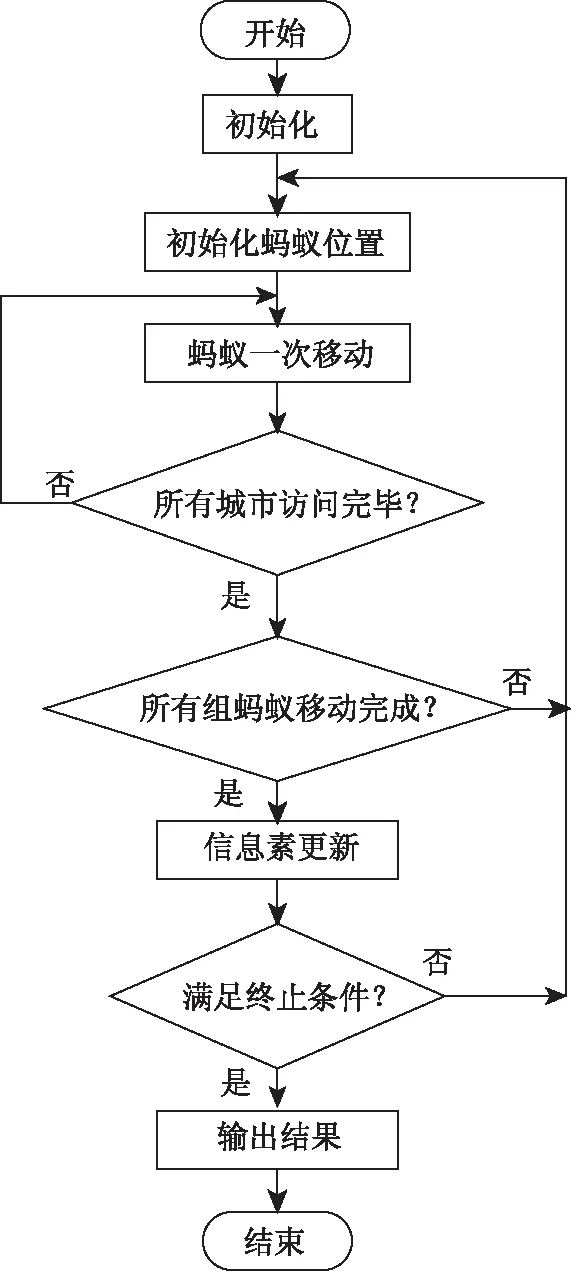
图5 多信息素蚁群算法流程图

Step1：算法参数初始化，包括蚁群组数量、最大迭代次数、信息素挥发比例、信息素最大更新次数等；

Step2：初始化信息素分布，初始状态时设置所有信息素为同一固定值。

Step3：进行各组蚂蚁的移动；

Step4：进行信息素的更新，包括信息素的衰减和增加；

Step5：若满足停止条件如达到最大迭代次数则算法停止输出算法结果；否则转Step3。

2.4 算法分析

多信息素蚁群算法中的蚂蚁和旅行商的互相选择的思路来自于合同网协议的合同签约流程，其选择的策略是在启发函数的基础上通过信息素含量进行调整，同时信息素的含量在不断学习中进行修正。由于问题中飞行平台在任务之间迁移时有一定的马尔科夫性质，即平台在任务之间的迁移代价与前置任务的关系较小，因此只保存任务之间迁移的信息素，减少了需要保存的信息。

原问题为NP问题，其复杂度为指数级。多信息素蚁群算法中，若旅行商个数为n，种群个体组数2n，每组蚂蚁个数m，迭代次数为c，蚂蚁移动中单次旅行商的选择复杂度为O(mn)，平台的选择为O(m)，所以蚂蚁移动完成的总复杂度为 O((mn+m)n)；信息素更新的复杂度为O(mn^2)。因此算法的总复杂度为O(cmn^3)，为多项式复杂度。在平台数量固定的情况下，随着任务数量的增加，算法单次迭代时间与任务数量的三次方呈线性关系。算法中的各组蚂蚁可以并行移动，信息素的更新也可以并行计算，因此算法可以通过并行计算，使得执行时间缩短。

3 仿真结果及分析

3.1 算法仿真结果

本文的仿真环境为i7+Windows下的Matlab，蚁群算法参数设置为：信息素挥发率0.2，种群个数为任务总数的两倍，迭代次数为100，启发因子为0.5。首先对一个简单实例进行仿真验证。该案例中，战场为1000 km×1000 km的矩形空间，共有8架飞行平台，分为三种类型，各类型的的数量分别为2，2，4，各平台的作战半径、移动速度、初始位置如表1所示；须执行任务共有8个，各任务的位置以及需求如表2所示。平台与任务的初始分布如图6所示。

表1 平台参数表

表2 任务参数表

图6 平台任务初始分布图

算法求解的结果如下：表3代表每个任务开始执行的时间；表4代表每个平台执行的任务列表，包括执行的任务编号和执行位置；图7中以平台为起点的曲线是根据平台路线模型得到的各个平台的飞行路线，这里的路线与表4的任务列表一一对应。对比表1和表2的参数，可以看到这个方案可以满足所有任务完成这个条件，且所有平台的执行任务点都在任务区内。

表3 任务执行时间表

表4 各平台执行任务顺序

续表4

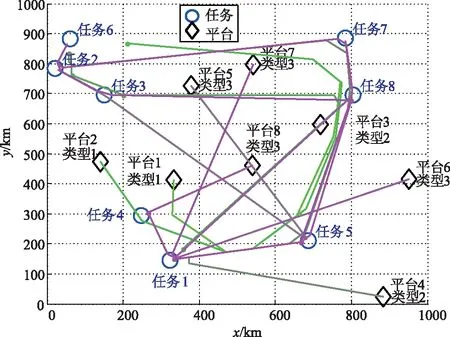
图7 平台估算航程图

算法收敛曲线如图8所示。对于此简单案例，算法最优值在迭代12次达到最低点，算法平均值也在迭代60次左右到达最低点且趋于平稳，算法收敛的最优解为3.04 h，是最后一个任务完成的时间。图中可以看到，算法具有随机寻优的特性，在算法初期算法最优值和平均值都有很大波动，代表算法在大范围的搜索；算法后期算法最优值和平均值波动较小，算法在进行局部的搜索，在小范围继续寻找更优解。

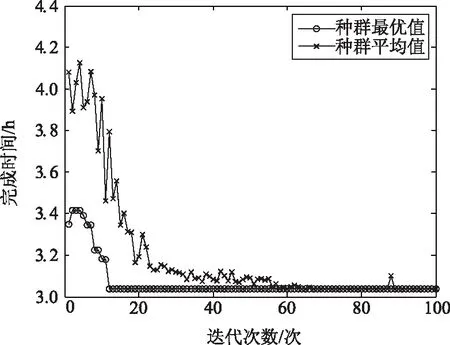
图8 算法结果收敛图

图9展示了算法迭代结束后，平台1对应的信息素的分布图。图中的九个端点中有八个代表着任务的位置，最后一个端点代表平台1的初始位置。图中线的粗细代表信息素的含量大小，线越粗代表这两个端点之间的信息素越多，也就代表平台更倾向于连续执行这两个端点代表的任务。由于任务2和任务3不需要类型1的平台参与，因此图中连接这两个任务的路线上的信息素很少。由图可知，信息素已经积累到了几条主要的线路上，几条线路可以组成由平台位置为起点的一条路径，该图中路径为起始位置-1-5-8-7-6，与平台1的任务列表1587相对应。方案中平台1并没有参与执行任务6，是因为平台2也可执行任务6，且两者执行效果相近，因而相持不下，并没有完全的淘汰掉其中一种，保留了两种可能性。

图9 平台1对应的信息素分布图

3.2 对比试验

对上述案例，同时运行多信息素蚁群算法与遗传算法，两种算法的最优解变化曲线如图10(a)所示。由图可知，两种算法最终求解的结果相差不大，但多信息素蚁群算法的收敛速度稍快一些，且有多次的下降，而遗传算法的下降点较少。因此，蚁群算法是在启发函数的指引下逐渐进化的，而遗传算法是更暴力的随机寻优，多次迭代才会找到更优解，且更优解可能效果变化会更大。

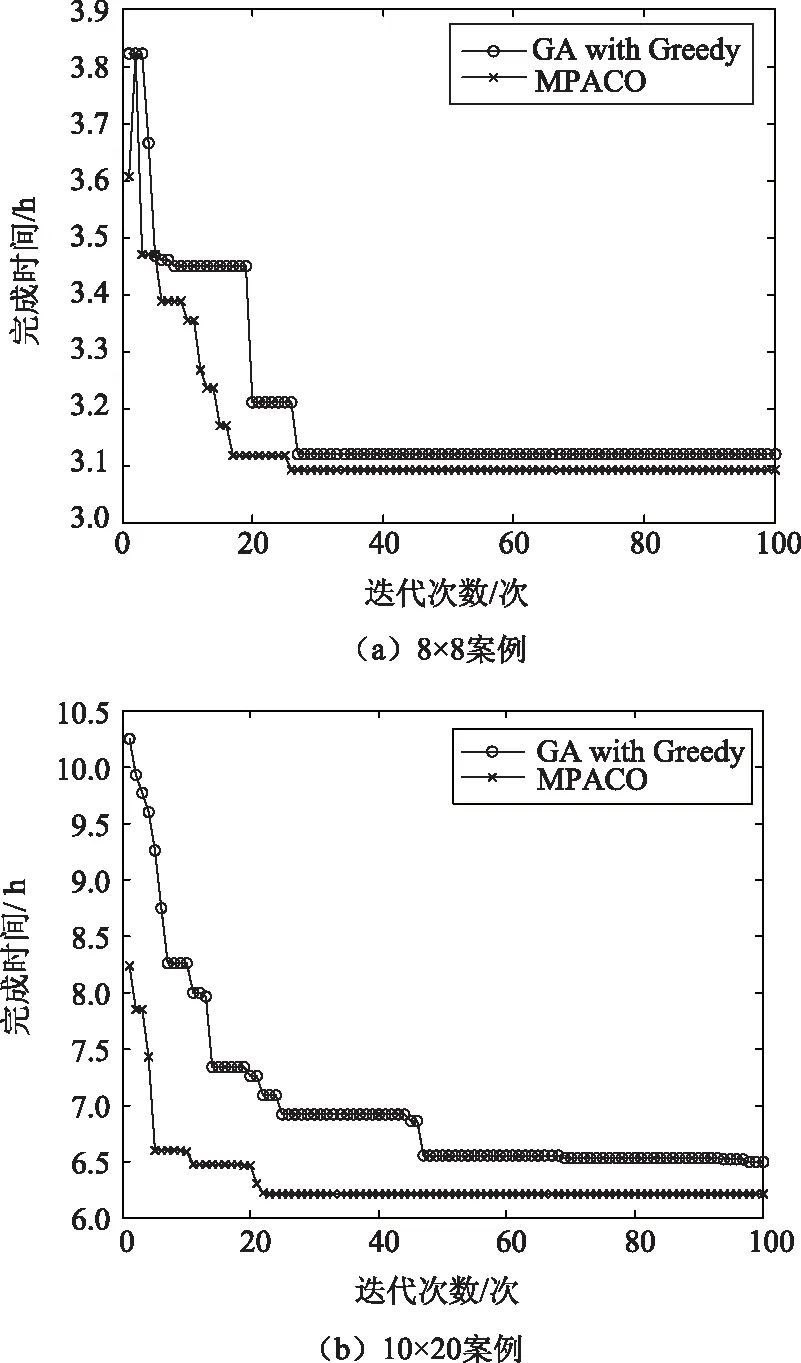
图10 算法收敛曲线对比图

下面对另一个复杂的案例进行算法对比，该复杂案例中任务数量为20，参与平台数目为10，其任务属性和平台属性由随机产生。两种算法运行结果对比如图10(b)所示。图中，最终两种算法求解的结果分别为6.21 h和6.50 h。多信息素蚁群算法在初始状态、收敛速度和收敛结果上都优于遗传算法。因此，在解空间很大的时候，遗传算法的随机产生的初始状态较差，且需要较长的时间搜索找到收敛的方向，而多信息素蚁群算法在启发函数的引导下，初始状态的结果就优于遗传算法，且最优解下降速度较快，最终也收敛到了更优的解上。

为了测试两种算法在任务数量与平台数量比例不同时的表现，在设定平台数量为8，任务数量为8-31之间，随机产生多组初始数据，算法运行后的平均结果如图11所示。在平台数量为8的时候，当任务数量小于12的时候，遗传算法的综合效果略好于多信息素蚁群算法，当任务数量大于或者等于12的时候，多信息素蚁群算法的效果超过遗传算法。任务数量在8-31范围时，多信息素蚁群算法效果平均优于遗传算法5%，分配结果任务完成平均时间差为0.37 h，两者相差最多的时候达到20%，时间差达到1.65 h。随着任务数量的增加，多信息素蚁群算法的效果与遗传算法相差越来越大。在求解TSP问题时，蚁群算法的效果优于遗传算法。而随着任务数量的增加，联合任务分配问题越来越趋近于TSP问题，因而由蚁群算法为基础的多信息素蚁群算法取得到更好的结果。因此，多信息素蚁群算法尤其适用于任务较多的情形。

图11 不同任务数量下算法结果对比图

3.3 算法运行时间

设定机群平台数量12，任务数量从1开始递增，算法的每次迭代时间与任务数量的关系如图12所示，其中横坐标X数值为任务数量的三次方。由图可知，算法单次迭代运行时间与任务数量的三次方成近似线性关系，与本文算法分析的结果相吻合。

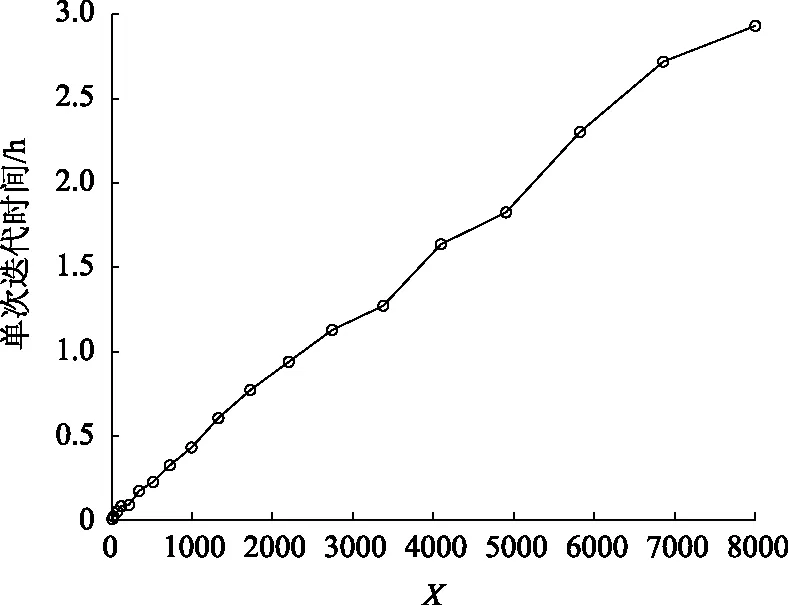
图12 算法单次迭代时间与任务数量曲线图

4 结 语

研究工作考虑到平台作战半径对联合任务分配的影响，建立了基于平台作战半径的路线模型，并将联合任务分配问题建模为复杂的多旅行商问题，通过图的方式将分配结果进行表示，改进蚁群算法，为每一个旅行商提供一种信息素并改变信息素更新策略，以图学习的方法求得图中边的组合作为任务分配的结果。仿真结果表明，该方法有效的解决了多类型平台共同执行多任务的任务分配问题，提供了稳定有效的解决方案。今后的研究重点将是动态环境下对分配方案的调整，以及在任务平台资源化描述的基础上资源调度的方法。