基于FFT算法的物联网终端网络自适应节点部署方法

刘 玲

(山东艺术学院,山东 济南 250013)

0 引 言

物联网是一种将传感器、用户和技术装置采用某种现代通信技术连接的信息化、智能化网络，物联网结构可分为网络层、中间层、应用层和感知层，其中感知层为物联网的终端，可有效连接信息世界和物理世界[1]，其通过有线或无线方法将不同仪器设备上的传感器有效连接，构成一个具有信息采集和控制功能的物联网终端网络。物联网终端网络中需要多个自适应节点共同完成某种工作，需要自适应节点具有较强的覆盖率和通信能力，因此需要对其进行合理部署。

目前，针对物联网终端网络自适应节点部署问题，已有一些专家学者提出了相关方法。如文献[2]提出了一种利用加权人工鱼群算法部署传感器节点的方法，引入标准人工鱼群算法并加入权重，用以自适应地选择人工鱼的视觉和步长，通过人工鱼觅食、聚群和追尾等行为，优化网络覆盖区域内传感器节点。但是经该方法部署后，有效节点的数量较少，节点覆盖率降低了；文献[3]提出了一种虚拟力扰动指数权值递减型粒子群算法，提高了粒子进入局部搜索的速度，并异构节点间的虚拟力来影响节点进化过程，得到了更多的覆盖率，但节点耗能偏高；文献[4]提出了一种基于VL图分割的节点自主部署方法，对目标区域做VL图划分并分配覆盖任务，分配到任务区间的节点通过构造VL受控多边形来确定下一轮目标位置，其它节点则计算所受虚拟力来确定下一轮目标点位置。同时网络各个节点逐轮更新自身位置。虽然该方法提升了有效节点的数量，但每一轮任务的覆盖率较低，节点耗能偏高，应用效果依旧不理想。

离散傅氏变换快速算法(Fast Fourier Transform，FFT)是一种用于信号处理和数据分析的算法，因此将FFT应用到物联网终端网络自适应节点的部署中，根据节点部署特点计算物联网终端网络覆盖率，再利用虚拟力算法和通信门限控制将节点间虚拟力控制在合理范围，在此基础上采用FFT算法构建虚拟力的函数模型并引入基函数矩阵，优化自适应节点间虚拟力，加强对自适应节点的优化部署，增加有效节点数量并扩大网络覆盖率。

1 物联网终端网络自适应节点部署方法

本文自适应节点部署方法的总体框架图如图1所示。其核心在于进一步的优化部署，见FFT变换算法加入到虚拟力函数模型中，从而优化节点间的虚拟力，完成优化部署。

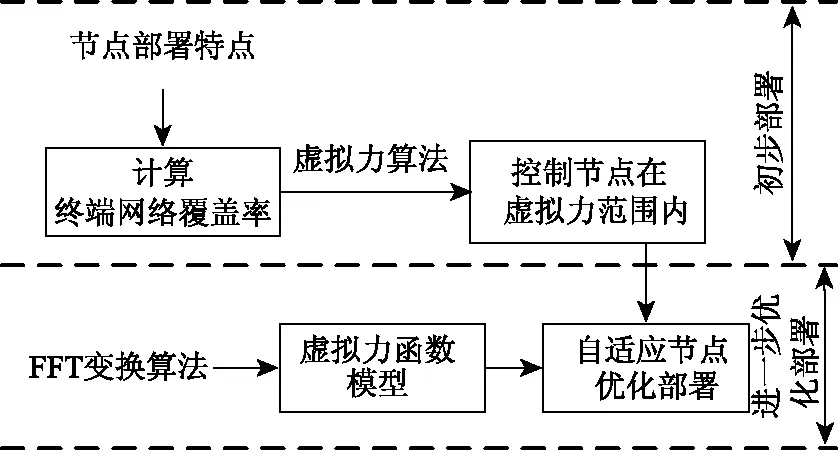
图1 本文总体框架流程图

1.1 物联网终端网络自适应节点部署特点

针对物联网终端网络的自适应节点部署特点，利用可移动自适应节点的移动特性，将物联网终端网络中的可移动自适应节点放置在由固定自适应节点部署的网络中，动态调整物联网终端网络的自适应节点，以达到提升网络覆盖率和通信能力的目的，且通过控制可移动自适应节点还可有效解决物联网终端网络中的目标跟踪问题。

将物联网终端网络中的所有自适应节点用集合S={si,i=1,2,3,…,n}表示，集合中的可移动自适应节点数量为k，固定自适应节点数为n-k，将物联网终端网络中所有自适应节点位置坐标用Z=[Xk,Xn-k,Yk,Yn-k]表示，其中可移动节点的横坐标和纵坐标向量分别为Xk={x1,x2,…,xk}和Yk={y1,y2,…,yk}，Xn-k={xk+1,xk+2,…,xn}和Yn-k={yk+1,yk+2,…,yn}分别表示固定节点的横纵坐标向量。

物联网终端网络中可移动自适应节点s对固定自适应节点t的感知概率P(s,t)可用公式(1)描述:

(1)

其中，d(s,t)表示物联网终端网络中可移动自适应节点与固定自适应节点距离，将可移动自适应节点的感知半径用r表示，e-λαβ为指数函数，re为感知半径最小值，α=d(s,t)-(r-re)，α为可移动自适应节点的可移动距离，λ和β分别表示d(s,t)在r-re和r+re半径变化时的衰减系数[5]。

采用公式(2)表示物联网终端网络的覆盖率：

(2)

式中，Scov-t表示待部署自适应节点T的集合，P(si,t)符合公式(1)的感知概率，表示物联网中可移动自适应节点Si对待部署固定自适应节点的监测概率[6]，将被部署自适应节点的被监测概率阈值用Pth表示，被部署节点符合式(3)时，说明部署自适应节点在被监测范围：

Pcov-t(Scov-t)≥Pth

(3)

将监测区域离散为m×n个方格，判断各个方格是否被可移动自适应节点感知覆盖可采用公式(3)，可采用公式(4)表示物联网终端网络的区域覆盖率：

(4)

其中Covw表示自适应节点范围内物联网终端网络的覆盖率。

1.2 自适应节点间的虚拟力运算

在保证物联网终端网络覆盖率高的基础上，还需控制自适应节点间虚拟力在合理范围内，使物联网终端网络达到稳状态。

虚拟力算法可计算物联网终端网络中传感器与目标障碍物以及网络中各自适应节点间的虚拟力，为物联网终端网络自适应节点寻找受力平衡[7]，使可移动节点移动到合理位置，实现物联网终端网络自适应节点的合理部署，由于自适应节点间存在通信距离受限的弊端，则在2.1小节获取的自适应节点范围内物联网终端网络的覆盖率的基础上，引入通信门限Gth，用作调控无法相互通信的自适应节点间的虚拟力[8]，使节点间距大于Gth时产生作用力等于零，将物联网终端网络中自适应节点j对i的虚拟力用式(5)表示：

(5)

式(5)中，Fi,j表示自适应节点i对j的作用力，自适应点i和j间直线距离用dij表示，κij用于描述自适应节点i到j的方位角，ηa和ηr分别代表虚拟力的引力系数和排斥力系数，二者主要作用是调控采用虚拟力算法后自适应节点部署结果的疏密[9]。

物联网终端网络自适应节点部署过程中，采用虚拟力算法计算得到自适应节点的综合受力后，可移动自适应节点在综合受力影响下，位置发生改变[10]，设置可移动自适应节点移动最大距离为MaxStep，自适应节点的移动距离与综合受力成正比且移动距离小于MaxStep，自适应节点移动距离如公式(6)和(7)所示：

(6)

(7)

上述公式中的X_VfaStep和Y_VfaStep分别表示物联网终端网络可移动自适应节点，分别在X轴和Y轴方向移动位移[11]，Fxy表示虚拟力合力，其在X轴和Y轴方向的分力为Fx和Fy，Fth表示自适应节点受虚拟合力的阈值，当自适应节点虚拟合力低于Fth时，说明该自适应节点处于稳定状态，位置无需改变，当物联网终端网络中所有可移动自适应节点均无需移动时，说明该网络达到稳定状态，初步实现物联网终端网络自适应节点的合理部署[12]，但虚拟力算法在计算自适应节点间虚拟力过程中容易受到外界环境的干扰，因此需要优化自适应节点间的虚拟力，提升物联网终端网络自适应节点的部署效果。

1.3 基于FFT变换算法的节点虚拟力优化

FFT变换算法用于优化物联网终端自适应节点部署时，选取物联网终端网络中自适应节点在某段时间内的虚拟力为优化对象，设各时间下的自适应节点虚拟力用(t1,F1)、(t2,F2)、(t3,F3)，……，(tm,Fm)表示，ti和Fi(i=1,2,…,m)分别为物联网自适应终端网络的时间点和虚拟力值，构建虚拟力的函数模型F(t)，同时符合误差χi=F(ti)-fi在物联网终端网络允许的置信区间，此时采用公式(8)表示F(t)：

(8)

式中参数n和B均为常数，其取值与实际物联网终端网络相关，δ为虚拟力系数矩阵。

快速傅里叶变换可对信号进行傅里叶变换，采用基函数矩阵Bi(t)=sin(Eit+Hi)变换公式(8)，得到如公式(9)所示的虚拟力的函数模型F(t)：

F(t)=δ1+δ2sin(E1t+H1+δ3sin(E2t+H2+

+…+δnsin(En-1t+Hn-1)

(9)

式中Ei和Hi与实际物联网终端网络的属性相关。

将FFT算法用于优化物联网终端网络自适应节点虚拟力，可通过取特定数值n=m代入公式(8)计算，当选取的m值较大时，F(t)结果误差较大，所以选择具体m值时，应尽量选数值较小一些，取值在1-4之间，则公式(9)可用式(10)表示：

F(t)=δ1+δ2sin(Ε1t+Η1+δ3sin(Ε2t+Η2+

δ4sin(Ε3t+Η3)

(10)

实际物联网终端网络中，若存在40个自适应节点，优化这些自适应节点在该网络中的虚拟力[13]，需采用式(10)来估计虚拟力Fi(i=1,2,…,40)实际值，计算n阶虚拟力系数矩阵δ=(δ1,δ2,…,δn)T，T为周期，实际自适应节点受到虚拟力m维矩阵函数为F=(f1,f2,…,fn)T，在不同时刻采样下估计的自适应节点虚拟力为F=(f(t1),f(t2),…,f(tm))T，根据公式(8)可得不同时刻采样下优化得到的自适应节点虚拟力矩阵表达式：

F=(f(t1),f(t2),…,f(tm))T=Bχ

(11)

此时的虚拟力误差向量为：

χ=Bδ-f

(12)

为保证虚拟力估计值与实际值差值最小，以误差向量的范数平方最小值作为优化目标[14]，可得：

(13)

若要使式(13)为极小值，将δb(b=0,1,2,…,n)带入式(13)，并对其进行偏微分处理，得到：

(14)

由式(14)可得式(15)所示关系式：

BTBδ=BTF

(15)

由于采用FFT算法时采用基函数矩阵为Bi(t)=sin(Εit+Ηi)，该矩阵为满秩矩阵[15]，则有BTB为正定矩阵，可将虚拟力系数矩阵δ用式(16)表示：

δ=(BTB)-1BTF

(16)

将BTB和BTF分别用常数D和Y表示，可得虚拟力矩阵系数根D-1Y，且有：

Dδ=Y

(17)

将FFT算法用于物联网终端网络自适应节点优化部署时，通常已知基函数矩阵和公式(8)，可将式(17)代入式(8)优化物联网终端网络自适应节点的虚拟力，提升自适应节点的部署效果。

2 实验分析

仿真分析本文方法应用在某实际物联网终端网络自适应节点部署的效果，采用本文方法对该网络中的自适应节点进行部署，为比较本文方法部署效果，将文献[2]中的基于人工鱼群算法的节点部署方法和文献[3]中的基于粒子群算法的自适应节点部署方法与本文方法进行比较。

2.1 有效自适应节点数

为实现物联网终端网络自适应节点部署，需确定物联网终端网络部署范围内有效的节点随时间变化的轨迹，实验选取的物联网终端网络详细信息如表1所示，有效自适应节点数随时间变化曲线用图2描述。

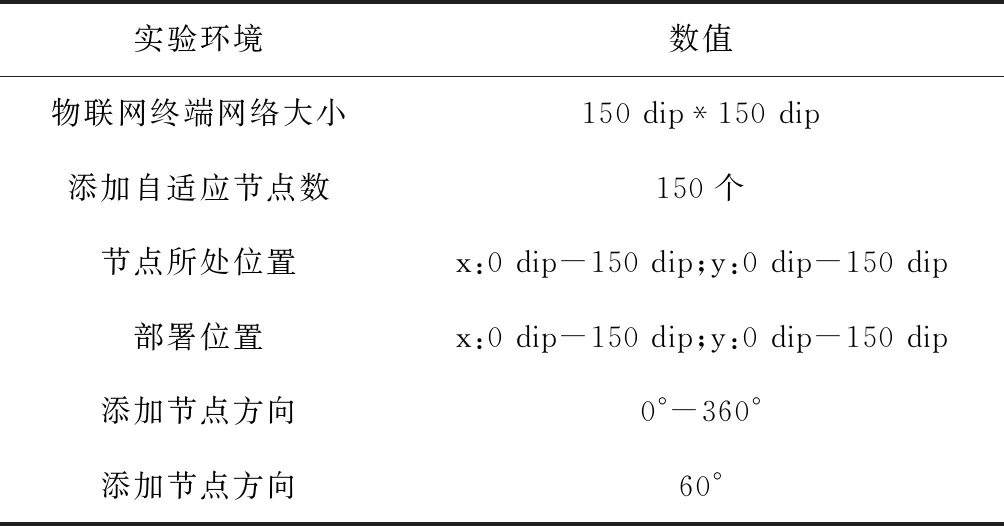
表1 物联网终端网络详细信息

图2 物联网终端网络有效自适应节点随时间变化结果

从图2曲线分析可知，人工鱼群部署方法和粒子群部署方法在实验开始初期，有效自适应节点增加速度较快，但随着时间增长，人工鱼群方法部署得到有效自适应节点数量几乎不再增长，在15个左右变化；粒子群方法在实验开始后20 s时，有效自适应节点数达到最大值15个，随着实验继续，有效自适应节点数量呈现减少-增加-减少的趋势，在实验结束时有效自适应节点数低于15个；而本文方法实验进行过程中产生的有效自适应节点数量一直增加，在实验结束时产生的有效自适应节点数接近50个，说明本文方法可有效增加物联网终端网络自适应节点数量，提升自适应节点部署质量。

2.2 网络覆盖率

同样在表1的实验环境下比较三种方法部署自适应节点后的网络覆盖率，物联网终端网络覆盖率越高，说明该物联网终端网络的通讯能力越强，将三种方法部署自适应节点后物联网终端网络的覆盖率用表2描述：

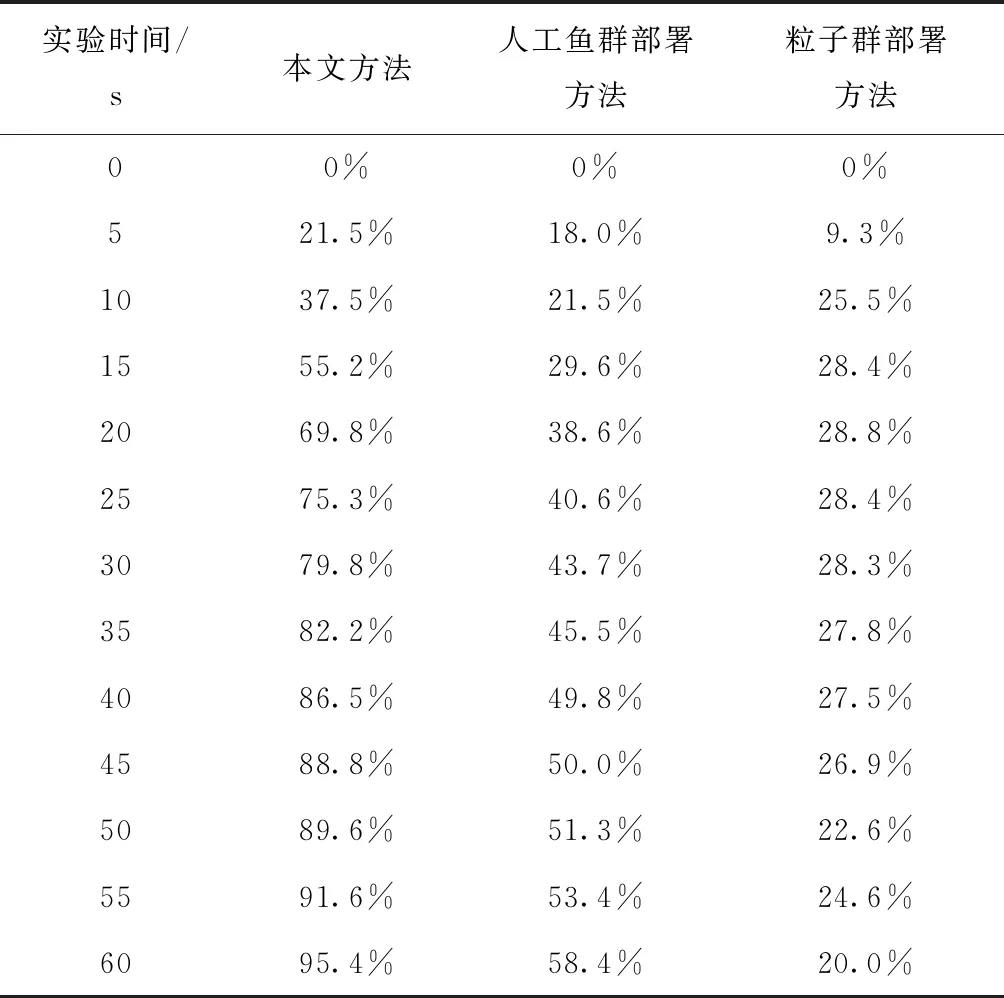
表2 物联网终端网络的覆盖率(%)

用图3描述三种方法自适应节点部署后物联网终端网络的覆盖率。

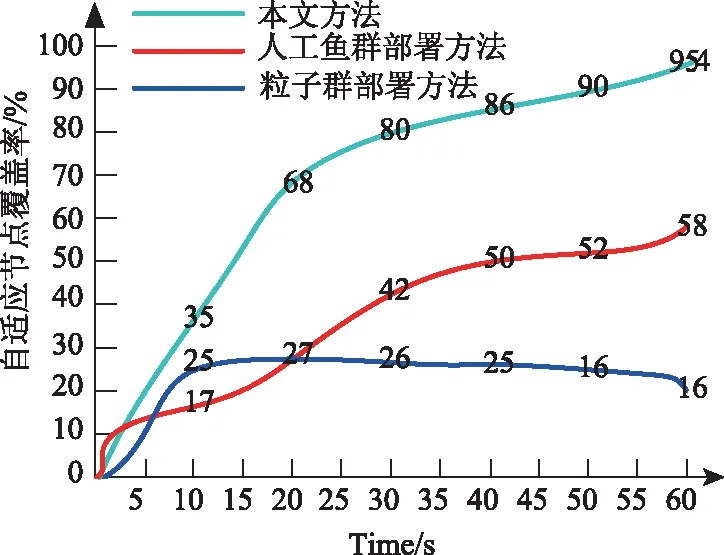
图3 物联网终端网络覆盖率曲线

分析表2和图3曲线结果可知，采用本文方法部署物联网终端网络自适应节点后，网络覆盖率随着实验的进行逐渐提升，覆盖率最高可达95.4%，而人工鱼群部署方法和粒子群部署方法在实验开始前20 s的网络覆盖率一直处于增长状态，随着实验进行，人工鱼群部署方法的网络覆盖率增长幅度有所降低，但始终处于增长状态，粒子群部署方法在实验开始20～45 s内的网络覆盖率变化十分微小，在45～60 s内物联网终端网络覆盖率降低幅度较大，说明采用本文方法部署自适应节点后网络覆盖率高，网络通信能力较强。

2.3 自适应节点能耗比较

物联网终端网络自适应节点的部署过程中，应严格控制有效自适应节点数量，以节省能源和资源；此外，在控制可移动自适应节点移动距离时，应以移动最短距离为部署条件，降低自适应节点的能源损耗。表3为一定数量有效自适应节点平均能耗，表4为可移动自适应节点移动一定距离能耗。

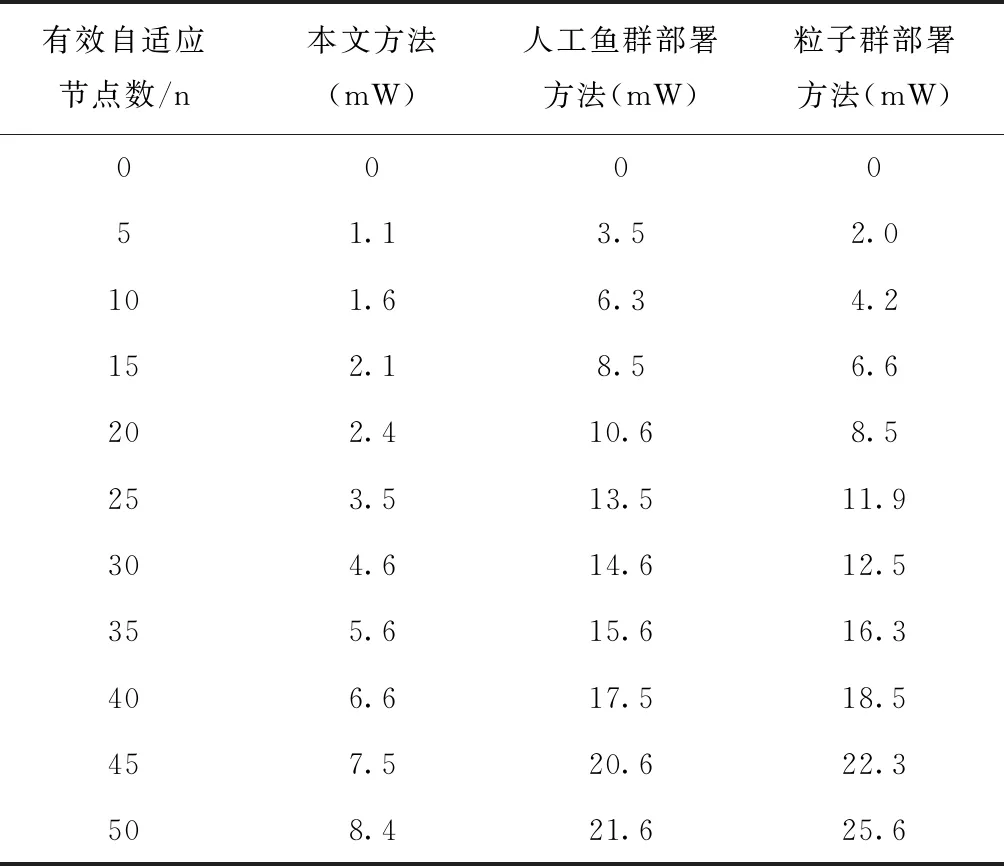
表3 一定数量有效自适应节点平均能耗(mW)

为突出比较不同三种方法在部署完物联网终端网络自适应节点后的节点平均能耗，将表3数据用图4所示曲线描绘。

图4 自适应节点平均能耗曲线

联合分析表3和图4可知，随着有效自适应节点数量的增加，节点的平均能耗一直在提升；从图4可知，本文方法部署完物联网终端网络自适应节点后，随着有效自适应节点数量的增加，有效自适应节点的平均能耗提升幅度较低，平均能耗最高为8.4 mW；人工鱼群部署方法和粒子群部署方法部署后，随着自适应节点数量的提升，节点的平均能耗提升较高，结果表明本文方法可有效降低自适应节点能耗，是一种高效节能的物联网终端网络自适应节点部署方法。

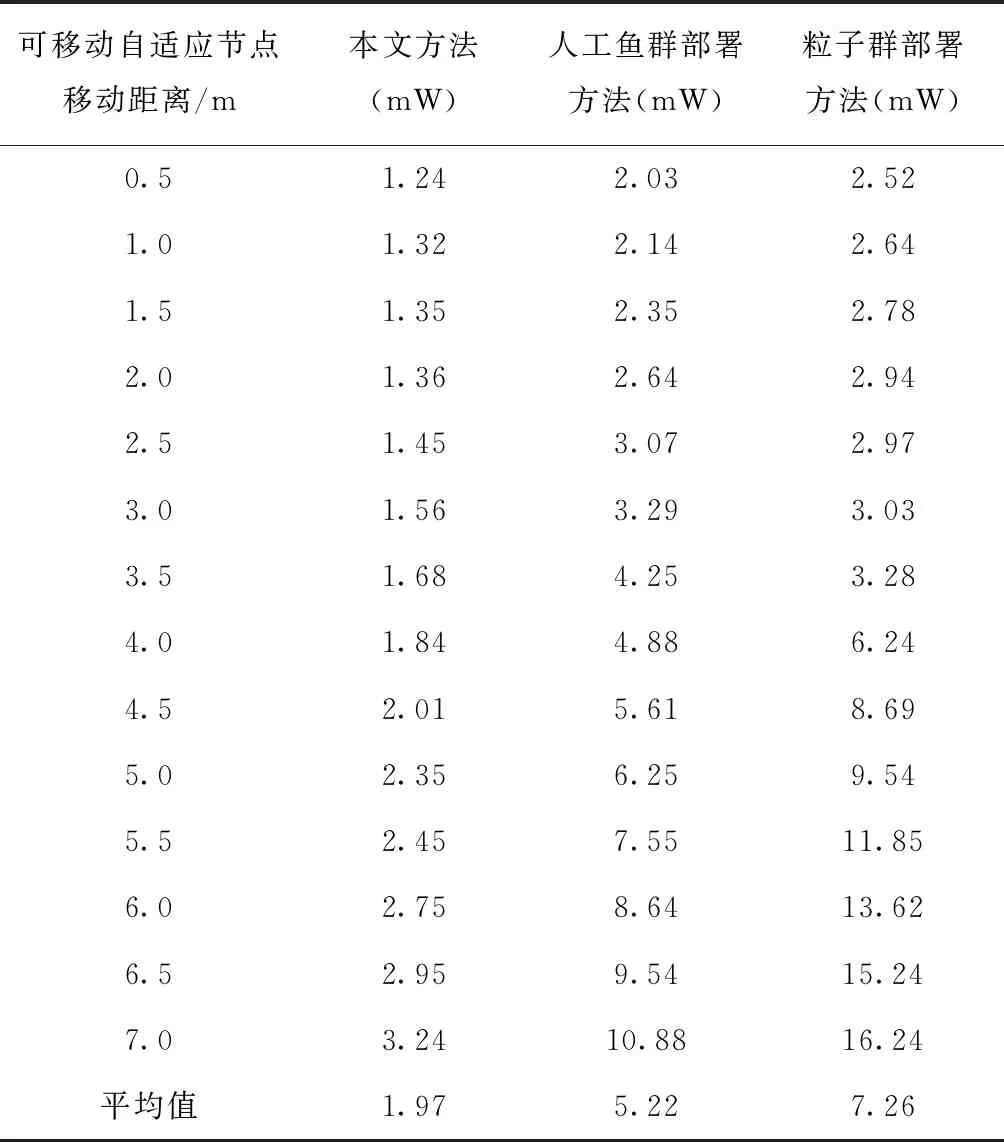
表4 可移动自适应节点移动一定距离能耗(mW)

分析表4数据结果可知，物联网终端网络自适应节点部署过程中，可移动自适应节点的移动距离越长，节点的能耗越高，详细分析表中数据可以看出，采用本文方法进行自适应节点部署后，可移动自适应节点能耗随移动距离的增加提升幅度缓慢；人工鱼群部署方法和粒子群部署方法在节点移动距离较短时，节点的能耗较低，当自适应节点移动距离为7.0 m时，节点的能耗最高。为详细了解可移动自适应节点在移动不同距离时的能耗情况，将表4数据结果用图5曲线描绘。

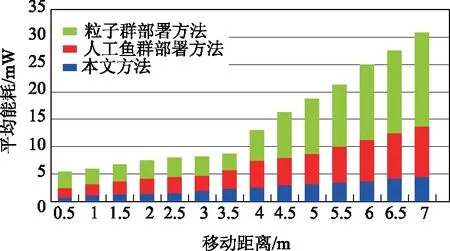
图5 可移动自适应节点移动不同距离的能耗曲线

从图5可以清楚得出，不同移动距离下可移动自适应节点的能耗大小为：粒子群部署方法>人工鱼群部署方法>本文方法，且三种方法部署后可移动自适应节点在移动距离小于3.5 m时的能耗较低，相差较小，但移动距离超出3.5 m后粒子群部署方法和人工鱼群部署方法的节点能耗提升较快，同样可说明本文方法是一种节能环保的物联网终端网络自适应节点部署方法。

综上所述，基于FFT算法的物联网终端网络自适应节点部署方法的网络覆盖率高、网络通信能力较强，且耗能较低。这是由于该方法首先根据节点部署特点计算了覆盖率，在已知覆盖率的基础上将节点间虚拟力控制在合理范围，实现了低能，再采用FFT变换算法构建虚拟力的函数模型并引入基函数矩阵，优化自适应节点间虚拟力，实现对自适应节点的优化部署。在实际应用，也具有类似于仿真实验的效果，只要控制好如表1相关参数，在实现过程中，加入的FFT变换算法可以采用已经固化到硬件的产品，一方面可以提高运行速度，另一方面提高稳定性。这样实施比采用智能算法更优化，因为固化的模块不仅运行速度快，而且准确。

3 结 语

本文提出基于FFT算法的物联网终端网络自适应节点部署方法，在所提方法中，合理的节点部署除保证网络的覆盖率外还需最大程度的保证网络的稳定性，采用虚拟力算法构建虚拟力函数模型，加强了物联网终端网络的稳定性；为提升自适应节点的合理部署，采用FFT算法，优化物联网终端网络自适应节点的部署效果，极大提高网络覆盖率，降低网络节点能耗。实验结果验证了所提方法的有效性。