一种基于密度峰值聚类的经典轨迹计算方法

李旭东，成 烽

(1.南京电子技术研究所，江苏 南京 210039；2.武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 430079)

0 引 言

不断普及的位置传感器、飞速发展的移动互联网、以及日益完善的通信基础设施，使得各行各业正在以越来越快的速度采集关于移动对象的轨迹数据。轨迹数据是按时间戳排序的一组位置点，同时集成了空间信息、时间信息和属性信息，并且蕴含了丰富多样的语义信息和行为模式。目前，针对轨迹数据的处理与分析已在越来越多的领域得到了应用，例如，理解动物迁徙过程中的移动轨迹从而开展动物生态与行为的研究[1]、基于历史轨迹与当前路径的台风灾害实时预警[2]，以及在智能交通系统中，获取与分析车辆轨迹信息以提高交通调度的效率[3]。

在轨迹数据激增和大数据技术发展的背景下，如何从轨迹数据中挖掘有意义的群体移动模式，已经成为轨迹数据分析领域的研究热点之一。Gudmundsson等提出了Flock移动模式[4]，对在指定圆形区域中连续移动至少k个时间片的移动对象进行了探测。为了克服Flock关于区域形状和群体大小的限制，Jeung等提出了Convoy模式[5]，不再强调移动区域的形状，仅要求对象群之间是密度相连的。Aung等考虑到在Convoy中，某些参与对象可能会暂时离开群体，提出了dynamic convoy 和evolving convoy模式[6]。Li等进一步弱化限制条件，即参与对象仅需持续k个时间片，且不一定是连续的，提出了更通用化的Swarm模型[7]。为了模拟游行、抗议、拥堵等群体事件，Zheng等提出Gathering模式[8]，用以表示大量对象时空聚集而形成持续且稳定的高密度区域。

经典轨迹计算用于分析具有相似移动路径的轨迹分组，属于一类典型的群体移动模式分析，其主要技术思想是度量轨迹之间的相似性，将大规模轨迹数据聚类成簇，并进一步发现轨迹簇的整体移动特征，从而用一条代表性轨迹来表征轨迹簇的群体移动模式。经典轨迹描述了大规模轨迹数据的群体移动特征，在刻画海量轨迹时空特征、分析群体行为模式和预测移动对象路径等方面具有十分重要的应用意义。在经典轨迹分析方面，Gaffney等提出了一种基于模型的轨迹聚类算法[9]，将其用于经典轨迹的生成；Jiawei Han等提出了基于轨迹分段思想的经典轨迹生成算法TRACLUS[10]；郑林江等人将轨迹映射到城市网格空间中，利用密度阈值提取热点格网[11]，并通过合并热点格网来寻找经典轨迹。

本文面向大规模轨迹数据，聚焦于群体移动对象的经典轨迹计算问题，提出了一种基于密度峰值聚类的经典轨迹计算方法，包括相似矩阵计算、轨迹聚类分析和经典轨迹生成三个前后无缝衔接的步骤。在相似性度量方面，我们采用并改进了顾及轨迹几何与方向的SSPD方法[12]；在轨迹数据聚类方面，我们引入了密度峰值聚类方法[13]，并使用其K近邻版本[14]，以消除参数选择的不利影响。考虑到在密度峰值聚类中，中心点表征了基于轨迹距离的局部密度最大轨迹，我们直接将轨迹蔟中心作为经典轨迹输出。基于船舶轨迹的实验表明，本文方法可以有效从大规模轨迹中分析出经典轨迹，且同TRACLUS算法相比，本文方法输出的经典轨迹更为真实自然。

1 经典轨迹计算框架

经典轨迹计算是指从轨迹群中选择一条或多条最具代表性的轨迹，其他轨迹与这些代表性轨迹中的一条具有相同或相似的行经路线，即分析大规模轨迹的频繁模式，属于一类典型的轨迹群整体移动模式挖掘方法。例如，通过分析船舶历史轨迹移动规律的相似性，生成其经典轨迹，可以用来预测当前船舶的可能移动路径。为此，本文提出了一个基于密度峰值聚类的经典轨迹计算方法，其分析框架见图1所示。

首先进行预处理，通过速度等阈值过滤掉噪声点，并采用高斯函数进行平滑处理。然后依次执行三个主要步骤：(1)相似度计算，(2)密度峰值聚类，(3)经典轨迹提取。相似度矩阵计算根据轨迹之间的相似度度计算出距离度量，并形成对称的相似度矩阵；密度峰值聚类以轨迹相似度矩阵为输入，采用密度峰值聚类算法进行面向轨迹的聚类处理，得到轨迹聚类簇的集合；经典轨迹提取对每一个轨迹数量达到阈值要求的轨迹聚类簇，选择其聚类中心对应的轨迹作为经典轨迹的输出。

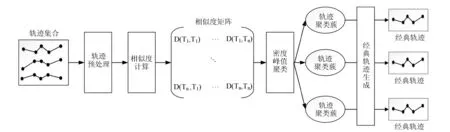
图1 基于密度峰值聚类的经典轨迹计算框架

密度峰值聚类算法将面向大规模轨迹数据，基于轨迹距离来搜索那些具有局部密度极大值，且距离更高密度中心较远的轨迹。显然，该算法不仅生成关于轨迹的聚类蔟，而且输出局部的聚类中心。在一个轨迹蔟中，聚类中心是具有最高密度的轨迹，自然成为该轨迹蔟的代表性轨迹，即经典轨迹，故本文的关键问题在于两方面，一是轨迹相似度计算，二是轨迹数据聚类。

2 轨迹相似度计算

轨迹相似度计算[15]通过衡量两条轨迹之间的相似程度，形成一个正的数值型距离值，越小表示轨迹越相似，取0则表示两条轨迹途径同一路径。显然，基于相似度的轨迹距离函数定义将直接影响到相似度矩阵的计算结果，进而关系到轨迹聚类结果的好坏。在轨迹相似性度量方面，学者们先后提出多种关于轨迹距离的定义，如欧式距离、DTW距离[16]、LCSS距离[17]、EDR距离[18]，等。由于轨迹采样频率不同、路径长度不一、存在噪声和漂移，以及具有方向性，我们期望轨迹相似度距离计算方法具备以下性质：(1)将轨迹作为整体来计算相似度；(2)允许轨迹具有不同长度；(3)满足三角不等式；(4)对噪声有一定健壮性；(5)不仅识别出轨迹形状上的相似性，而且考虑轨迹点的位置与方向。

为此，我们选择SSPD(Symmetric Segment Path Distance)距离，其计算原理见图2所示。首先计算轨迹A上每一个轨迹点到轨迹B上连续两个点所夹线段的最小距离，然后累加这一点-线段距离，并除以轨迹A上轨迹点的数量，即得出轨迹A到轨迹B的距离。类似的，计算出轨迹B到轨迹A的距离，并将到轨迹A到轨迹B的距离和轨迹B到轨迹A的距离求和之后取平均，最终得到轨迹A和轨迹B的SSPD距离。

图2 轨迹的SSPD距离计算

在SSPD距离计算中，轨迹A上某个点投影到轨迹B上某个线段后，轨迹A上后续点只能投影到轨迹B上后续线段，因此，SSPD距离除了顾及形状与位置相似性之外，还能够区分出方向差异。此外，SSPD支持非等长轨迹的距离计算，并且是对称的，可度量的，即满足三角不等式。平均值处理固然使得SSPD距离在一定程度上降低噪声的影响，但在某些情况下将严重放大噪声点的影响，使得本来相似的两条轨迹之间距离变得特别大，如图3所示。

图3 带噪声点的SSPD距离

在轨迹A中，点A3是一个噪声点，由于SSPD距离在计算点—线段投影时不能回溯，使得轨迹A在噪声点A3之后的点全部匹配到轨迹B的尾点B5，导致累积之后的误差变得十分可观。为此，我们从以下两方面来改进SSPD距离的计算，使之对于噪声数据更为鲁棒：

(1)允许回溯k个点。计第i个点的投影距离为d1，计算其到第(i-j)(k≥j>0)个点的投影线段及后续线段的最小投影距离d2，如果d1/d2超过某一阈值，那么将作为d2作为第i个点的投影距离，相应线段为第i个点的匹配线段；

(2)如果当前点的最终投影距离超过某一阈值，将该点标记为噪声，不参与SSPD距离的计算，从而消除噪声点的影响。

在图3中，如果A3到B4B5的投影距离大于阈值，改进的SSPD距离将其标记为噪声点，后续点将从B1B2尝试投影；否则的话，A3投影到B4B5，A4则可以跳过A3，其投影的目标线段可以回溯到B1B2，从而正确投影到B2B3。

3 基于轨迹距离的密度峰值聚类

经过相似度计算之后，任意两条轨迹之间的距离被量化为一个零维数值，从而形成一个相似度矩阵，在此基础上有多种聚类算法可供选择，如K-MEANS[19]、DBSCAN[20]等，但是，面向轨迹的聚类算法应具备以下特点：(1)挖掘出轨迹长程运动模式，(2)发现任意形状的簇，(3)对全局参数不敏感，(4)不需要先验知识。为此，我们选择2014年发表于《Science》期刊上的密度峰值聚类算法[13]。该算法的核心思想十分简洁，基于两个朴素的假设来确定聚类中心：(1)聚类中心是局部密度的最大对象；(2)聚类中心到其他聚类中心的距离相对较远，以不被归入其他聚类中心所属聚类簇内。密度峰值聚类算法对于任意一条轨迹Ti，需要计算局部密度ρi和上向距离δi，即到更大密度聚类中心的最小距离。ρi和δi的定义分别如下：

(1)

(2)

其中，dij为轨迹Ti和Tj的相似度距离，而dc为截断距离。从定义不难发现，局部密度的计算易受截断距离dc的影响。在数据规模较大时，局部密度的计算结果对于截断距离dc有一定的健壮性，而在数据规模较小时，由于数据分布不一定符合真实分布情况，此时截断距离取值的影响不可忽略。为此，我们引入一种改进策略，将K最近邻思想引入到局部密度计算中，从而形成基于K最近邻的密度峰值聚类算法[14]，其局部密度ρi的定义被修正为如下所示。其中，KNN(i)为样本Ti的的K最近邻轨迹集。

(3)

由于不需要设置硬性的截断距离dc，局部密度计算在不同规模数据集中是自适应的。当样本Ti到其K最近邻的距离越小，局部密度越大。基于K最近邻的密度峰值聚类算法虽然也存在K值的选取问题，但对于聚类效果的影响较小，且不会改变对聚类簇中心的选择。

在完成所有轨迹的局部密度和上向距离计算之后，便可生成一个横轴为局部密度，纵轴为上向距离的二维决策图。在决策图中，那些局部密度ρ与上向距离δ较为突出的对象将被视作聚类簇中心，即拥有较大上向距离且局部密度大于阈值的对象。当得到聚类中心之后，进一步可对所有轨迹进行聚类簇分配，将每条轨迹分配到距离最近，且密度大于自身的轨迹所属的聚类簇中。

4 经典轨迹生成及实验

4.1 经典轨迹生成

当计算得到轨迹簇集合以后，下一步需要从每一个轨迹蔟中找到最能代表本簇整体移动趋势的经典轨迹，主要有三类代表性方法：(1)最优代表法，从轨迹簇中选出一条最具代表性的轨迹作为经典轨迹输出，(2)等间距合并法，等距重采样轨迹簇中的轨迹，据此计算重采样点的平均坐标，从而输出形成经典轨迹，(3)扫描线法，首先确定轨迹蔟的整体运动方向，进一步得到轨迹蔟的扫描线，然后计算扫描线与簇中轨迹的相交点，以其平均坐标来形成经典轨迹的时空点。后两种方法输出的是合成轨迹，可能在轨迹蔟中没有任何一条轨迹的路径与此相似，使得其输出只是拟合了轨迹蔟的时空分布，但偏离了用户对于经典轨迹的认知。此外，这两种方法的计算比较耗时，其计算复杂度将随着轨迹数目和采样点数量的增加呈指数级增长。

为此，我们选用最优代表法来输出经典轨迹，由于不需要形成合成轨迹，其实现较为简单，计算非常高效。一种直观的实现最优代表法的策略是针对每一个轨迹簇，将每条轨迹到其他轨迹的相似度距离之和作为该轨迹的分数，从而选择得分最高的轨迹作为该轨迹蔟的经典轨迹。具体到密度峰值聚类算法中，聚类中心是具有局部密度极大值，且距离更高密度中心较远的轨迹，即在一个轨迹蔟中，聚类中心是具有最高密度的轨迹，也就是说，其他轨迹到该轨迹的距离之和是最小的，因而可以输出为该轨迹蔟的代表性轨迹，即经典轨迹。

4.2 经典轨迹实验

实验数据为模拟产生某海域的船舶轨迹。这个轨迹数据集包含约6百条行船记录，共计17736个轨迹点，其中，每一条轨迹包含船舶的经度、纬度、时间戳和编码。图4展示了该轨迹集的密度峰值聚类决策图，其中，横坐标和纵坐标分别表示局部密度和上向距离。

在决策图中，局部密度与上向距离同时较大的轨迹将形成一个轨迹蔟，且该轨迹作为该轨迹蔟的聚类中心，输出成为代表该轨迹蔟的经典轨迹。实际上，轨迹的时空分布可能异常复杂，轨迹蔟的界定并不是一件很容易的事情。以图4为例，点1和点2所代表的轨迹簇聚类效果较为显著，点3虽然局部密度不大，但有较大的上向距离，仍可作为一个轨迹聚类簇(聚集的轨迹数量虽少，但其空间走向不同于其它轨迹，仍然是目标所走的路径之一)。后续选择哪些轨迹来形成聚类中心，却很难清晰地确定出来。尽管如此，决策图给出的关于轨迹聚类信息有比较直观的呈现，是一个较好的辅助用户选择轨迹蔟及输出经典轨迹的可视化工具。

图4 船舶轨迹的密度峰值聚类决策图

在进一步分析图4的聚类决策图之后，我们将轨迹蔟数量最终选定为5，即输出5条经典轨迹，见图5a)所示，图6进一步展示了其中2条经典轨迹所代表的轨迹蔟。与此同时，我们也采用TRACLUS算法来计算船舶数据的经典轨迹，见图5b)所示，共输出6条经典轨迹。不难从图5和6看出，密度峰值聚类方法输出的经典轨迹是真实存在的，即对于每一条经典轨迹来说，有大量轨迹沿着相同或相似的路径移动，而TRACLUS方法输出的经典轨迹是合成的，虽然比较符合轨迹数据的时空分布，但实际上很少有真实轨迹是沿此路径移动的。以图5b)上方输出的长直线经典轨迹为例，没有任何一条船舶轨迹的走向与此该路径相同或相似。因此，同TRACLUS方法相比，密度峰值聚类算法是一种行之有效的经典轨迹计算方法

图6 船舶轨迹的轨迹簇示例

5 结 语

在轨迹数据激增和大数据技术发展的背景下，如何从大规模轨迹数据中挖掘有意义的群体移动模式，已经成为轨迹数据分析领域的研究热点之一。经典轨迹是群体轨迹移动时呈现出的相同或相似路径，但由于存在漂移噪声、非均匀采样、起止点不一致等原因，经典轨迹计算并不是一件容易的事情。考虑到经典轨迹在其局部存在大量相似的轨迹，本文提出了一种基于密度峰值聚类算法的经典轨迹计算方法，首先采用顾及轨迹几何与方向的SSPD方法来计算轨迹相似度，然后引入了密度峰值聚类算法来聚类轨迹数据，最后直接将峰值点对应的轨迹输出为经典轨迹。

本文的贡献主要有三方面：(1)提出了一种基于密度峰值聚类的经典轨迹计算框架，其计算过程更为简洁有效，(2)从噪声抑制和回溯匹配两方面改进了SSPD距离的计算，消除了噪声点对于轨迹距离的放大效应，(3)顾及了轨迹数据的复杂特征，采用K最近邻思想来计算轨迹的局部密度。基于船舶轨迹的实验表明，本文方法可以有效从大规模轨迹中分析出经典轨迹，且同TRACLUS算法相比，输出的经典轨迹更加真实自然。