基于迭代双重扩展的Kalman滤波的有源目标估计算法
陆 玉,张 华
(阜阳职业技术学院,安徽 阜阳 236031)
0 引 言
全球定位系统(Global Positioning System, GPS)已广泛应用有于有源目标的估计。然而,GPS系统并不适合室内目标的定位[1-2]。而基于到达时间差(Time Different of Arrival, TDOA)信号的定位算法广泛应用于室内定位[3]。基于TDOA信号的定位是利用双曲线轨迹,估计目标位置。即双曲线的交点就是发射机位置。但是,基于TDOA信号的定位算法存在超定问题。若需准确估计发射机位置,需测量更多的TDOA信号,增加了对发射机数量的要求。
此外,噪声也是影响基于TDOA定位精度的重要原因。文献[4]通过在二维和三维空间内的TDOA测量,消除与距离无关的噪声。它先建立与距离无关噪声模型,再基于源定位提高TDOA信号测量。
而测量移动发射机的位置和速度,可预测雷达和导航系统的未来轨迹。此外,测量到达频率差(Frequency Different of Arrival, FDOA)可以降低对接收机数量的限制。
为此,本文考虑只有两个接收器的场景,并通过FDOA信号测量移动发射机速度。再通过结合TDOA和FDOA测量,进行定位。同时,考虑RF系统噪声对测量值的非线性影响。并通过迭代双重扩展Kalman滤波(Dual-extended Kalman Filter, DEKF)算法对非线性误差进行补偿。依据迭代DEKF算法,参数估计(Parameter Estimation, PE)滤波更新因外部噪声造成的模型不确认性,并通过迭代,加速系统参数的收敛性。仿真结果表明,提出的ID-EKF算法有效地降低估计误差。
1 系统模型
由一个发射机和两个接收机构成定位系统。发射机以不同速度移动,并发送RF信号。令二维坐标r0=[x,y]T表示发射机位置。两个接收机位置表示ri=[xi,yi]T,且i={1,2}。

‖ri(k)-r0(k)‖
(1)
其中‖·‖表示范数。
RF信号达到接收机的时间:
(2)

(3)
其中t21(k)表示两个接收机接收RF信号的时间差。
通过两个接收机所接收的信号参数,可推导TDOA信号Td(k):
‖r1(k)-r0(k)‖+η(k))
(4)
其中η表示零均值的高斯白噪声。
接下来,用FDOA信号估计发射机的速度。由于多普勒效应,如果移动的接收机从发射机所接收的信号频率不同于发射频率。因此,引入平均频率fi(k),其表示在时间段Ts内的平均频率,其定义如式(5)所示:
(5)

FDOA测量阶段要求接收机同步。通过时间微分,便可获取FDOA信号:
(6)

结合式(1),通过时间微分,能够建立发射机的未知位置r0方程:
(7)
2 基于迭代的DEKF的定位算法
2.1 状态等式的建立
本节将发射机位置和速度转化状态变量,便以DEFK处理,如式(8)所示:
s(k+1)=As(k)+Bu(k)+w(k)=
f(s(k),u(k))+w(k)
(8)

用4维矢量表示接收机的位置和速度信息,如式(9)所示:
(9)
将TDOA和FDOA的信号测量值作为输出等式。令r1、r2∈R2表示两个接收机位置、令v1、v2∈R2表示两个接收机的速度。相应地,令r0、v0表示发射机的位置和速度。依据这些变量符号表示输出等式:
z(k)=h(s(k))+n(k)=
(10)

z(k)∈R2的第一项表示TDOA的测量值;第二项代表FDOA的测量值。而n(k)表示z(k)的噪声测量项。为了能将输出等式应用于迭代的DEFK算法,通过偏微分完成线性操作。先求式(10)的梯度:
(11)
其中vi=[Δxi(k)/Ts,Δyi(k)/Ts]T。
然而,在真实环境中,TDOA和FDOA的信号受到外部噪声影响[6]。这些外部噪声导致模型的不确定性,降低了迭代算法的性能。此外,外部噪声也延缓了收敛速度。
外部噪声主要由非视距(Nonline-of-sight, NLOS)噪声和测量噪声组成。本文,将TDOA和FDOA测量看成LOS数据[7]。而测量噪声是由环境因素引起的,如传感节点故障,环境温度和湿度的变化也增加定位误差。为此,引用迭代DEKF算法降低测量误差。
2.2 DEKF算法
为了提高定位算法,引用迭代EKF算法。文献[8]证实,迭代EKF算法的性能优于EKF算法。DEKF算法可以组织成状态滤波和PE滤波。每个滤波均能估计状态等式的未知参数。具体而言,状态滤波驱动PE滤波去估计状态等式的未知参数,而状态滤波依据当前的参数值估计状态,其形式化表述如式(12):

(12)
其中f(·)和h(·)分别表示式(8)、式(12)所示的状态等式和输出等式[9]。而r(k)表示m(k)的过程噪声。为了将迭代DEKF算法应用于定位问题,对每个滤波器的状态值和误差协方值进行初始化:
(13)
(14)

为了提高定位精度,应在每个抽样时刻更新状态等式。状态滤波s(k)的更新过程如下:
(15)
(16)

接下来,对PE滤波器m(k)进行更新,如式(17)所示:
(17)
(18)

在ID-EKF算法的状态滤波中,将测量更新等式进行线性迭代,如式(20)所示:
(19)

(20)
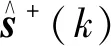
而PE滤波器的迭代测量更新方程,如式(21)所示:
(21)

(22)


图1 ID-EKF算法框架
3 性能仿真
3.1 仿真环境
考虑如图2所示仿真环境,两个接收机初始位置分别为(5,7)、(5,11),并可在以初始位置为中心,以1 km为半径的圆内移动。假定外部噪声和干扰信号服从高斯分布。
此外,测量的TDOA信号含有噪声,且所测量噪声协方差为0.0067。而速度状态(ϑx,ϑy)的协方差分别为0.1715和0.2251。在仿真过程中,发射机沿着sine波行轨迹移动,如图2所示。
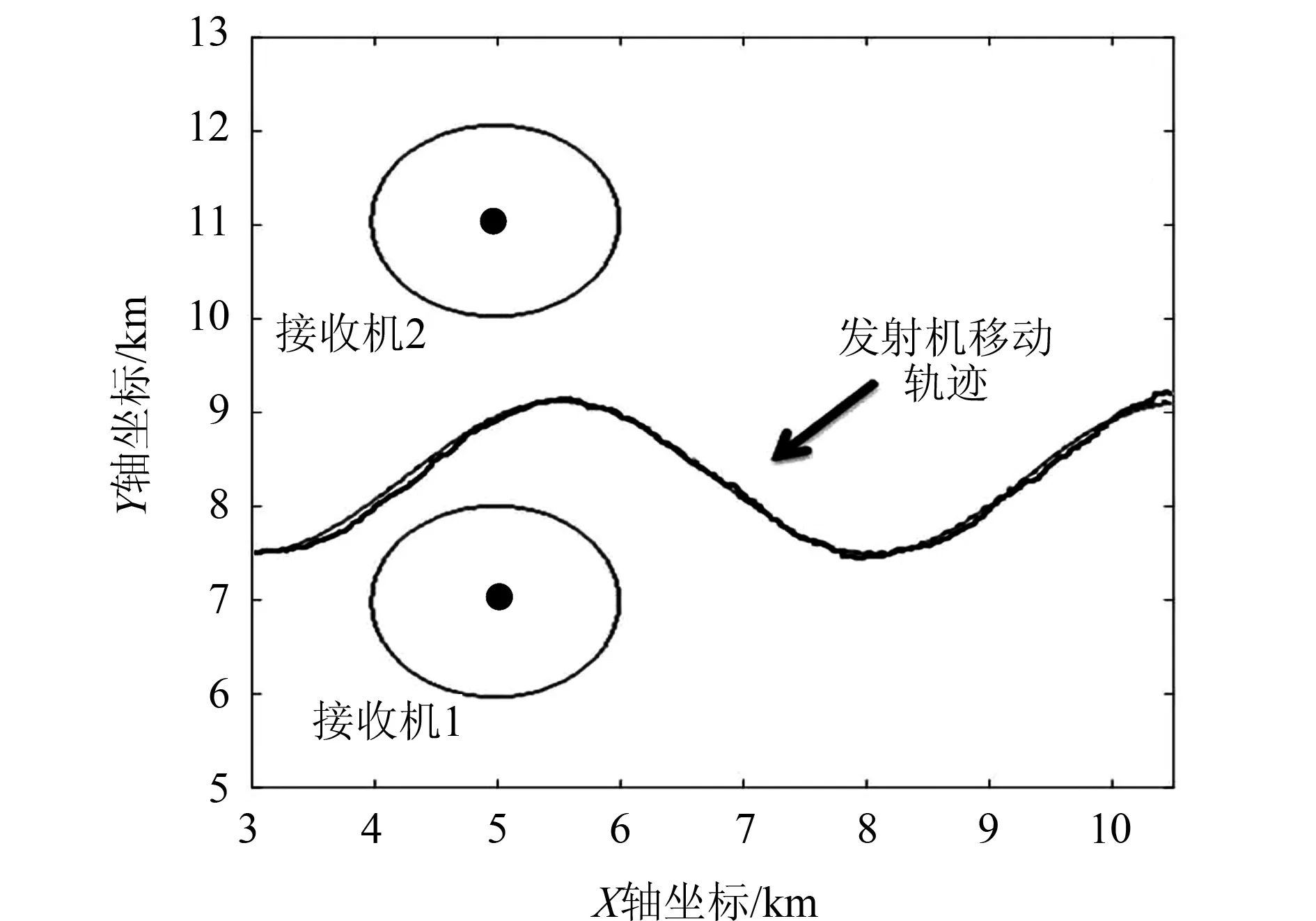
图2 仿真模型
3.2 数据分析
3.2.1实验一

图3 ID-EKF算法对发射机轨迹的估计
图3显示ID-EKF算法对发射机移动轨迹的估计。从图3可知,利用迭代的DEKF算法所估计的轨迹更接近于发射机移动的真实轨迹。同时,图3显示了3次迭代-DEKF和5次迭代DEKF算法对发射机移动轨迹的估计。
从图3可知,ID-EKF算法通过误差补偿能够提高对发射机移动轨迹估计的精度。原因在于:PF滤波能够估计状态等式的未知参数估计。同时,迭代次数的增加,也提高了估计精度。
3.2.2实验二
本次实验进行同类算法的对比分析。选择EKF、递归最小均方误差(Recursive Weighted Least Square, RWLS)[7]和Cramer-Rao 下限(Cramer-Rao Lower Bound, CRLB)作为参照。图4显示了噪声参数κe对RRSE的影响。

图4 RMSE随噪声参数κe的变化情况
噪声参数κe越大,外部噪声越严重。从图4可知,κe的增加,使RRSE增加,降低了估计性能。相比于EKF、RWLS,提出的ID-EKF算法有效了降低了估计误差,提高了发射机的估计精度。但与CRLB还有一定距离。
4 结 语
针对有源目标的估计问题,提出基于迭代双重扩展的Kalman的有源目标估计算法ID-EKF。为了准确估计发射机的速度,ID-EKF算法将FDOA信号作为测量等式。此外,为了降低计算负担,只考虑两个接收机,并利用迭代DEKF算法实现定位。为了能跟踪目标,建立关于位置和速度的状态等式和关于TDOA和FDOA信号的测量等式。迭代DEKF算法由状态滤波和PE滤波构成,其中PE滤波提高收敛速度,并降低误差。仿真数据表明,提出的ID-EKF算法降低估计误差,提高了对有源目标跟踪精度。

