基于运动外辐射源的单站定位误差分析与仿真

关 欣,舒益群,衣 晓

(海军航空大学，山东 烟台 264001)

0 引 言

外辐射源定位技术不主动发射电磁波，而是通过接收来自于辐射源的直达波以及经由目标散射的散射波，经过相干处理来解算出目标的位置[1]。与主要依靠有源雷达的定位方式相比，外辐射源定位隐蔽性高，抗干扰能力强，并具有探测隐身目标以及低空突防目标的能力，具有较高的研究价值[2]。

不同外辐射源定位方法需要的接收站数目或者辐射源数目不尽相同，同时对于接收站或是辐射源运动状态的要求也不同[3]。按照接收站的数目划分，可以划分为单站定位与多站定位。其中单站定位不需要接收站之间的配合，在使用时最为灵活，对于战场资源的依赖较小。

外辐射源定位的定位误差主要来自于三个方面：各个观测量的量测误差、辐射源位置的不确定性、不同定位方法的误差分布特性。各个观测量的量测误差主要来源于各自观测量采用的测量方法以及器件的内部噪声。精准的辐射源位置是利用辐射源进行定位的基础，也是保证目标定位精度的前提。不同的定位方法由于采用的观测量不同，当接收站、辐射源以及目标这三者的相对位置、运动状态变化时，定位误差的变化规律不同[4]。

在前人的研究中，人们大多关注的都是量测误差以及收发站布局对于定位误差的影响，而忽视了辐射源位置不确定性对于目标定位误差的影响。而在实际的定位过程中，选取的辐射源往往是非合作的，一般需要先获取辐射源的位置信息才能进行对目标的定位。这样的辐射源位置带有较大的误差，并且会影响目标定位结果。鉴于此，本文针对两种典型的单站定位方法，研究了辐射源位置不确定性对于定位误差的影响。

1 定位原理

单发单收定位算法模型[5]示意如图1。辐射源向外发射电磁波，有一路信号直接到达接收站，称为直达波；另一路信号经有目标散射到达接收站，称为反射波。

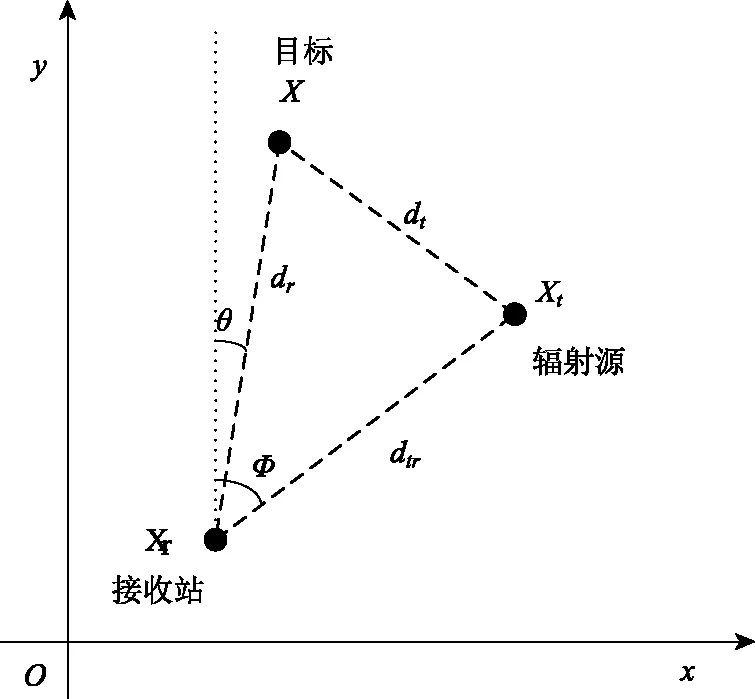
图1 单站单收定位模型

在整个定位过程，接收站能得到的参数有目标方位角θ、辐射源方位角φ、到达时间差TDOA、多普勒频差FDOA。本文不研究量测误差对于目标定位误差的影响，因此不谈论各个量测量的获取方法以及各自量测误差影响因素。但是辐射源位置的不确定性会给观测量φ、TDOA、FDOA带来不确定性，导致对目标的定位会出现定位误差。

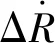
(1)

(2)

ΔR=dt+dr-dtr

(3)

(4)

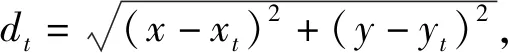
2 目标定位误差分析

在对目标进行定位时，目标在空间中不同位置或者目标、接收站、辐射源三者相对位置不同时，目标的定位误差不同。当三者相对位置固定时，采用不同的定位方法所得到的定位误差也是不同的。由于定位算法繁多，本文仅选取两种典型的单站定位算法，对其定位误差进行分析。本文采用几何定位精度GDOP(Geometrical Dilution of Precision)来描述目标的定位误差[7]，GDOP的定义如下：

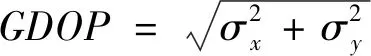
(5)

其中，σx，σy为X轴、Y轴方向定位误差的均方差。

2.1 DOA-TDOA基线联合定位

利用到达角、路径差以及长度可以实现对目标的定位。由余弦定理可知，

(6)

将(3)式代入得

(7)

由此可以得到目标的位置为

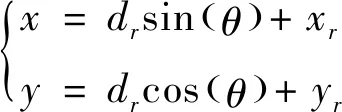
(8)

对式(8)两端同时求偏导，假设X轴方向与Y轴方向的位置误差互不相关，都是统计独立的高斯白噪声，用σxt,σyt分别表示X轴方向与Y轴方向的位置误差标准差，根据GDOP的定义式可知：

(9)

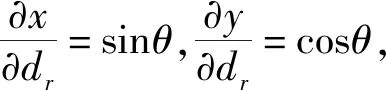
2.2 DOA-TDOA多普勒频移联合定位

(10)

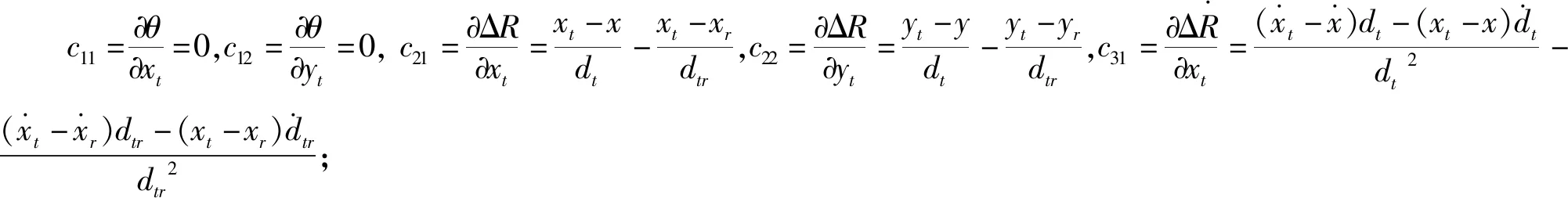
dY=CdXt

(11)

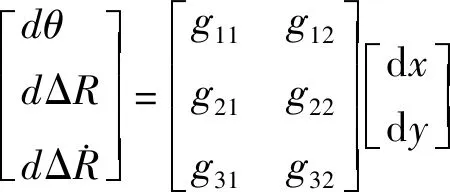
(12)

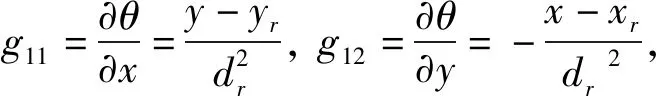
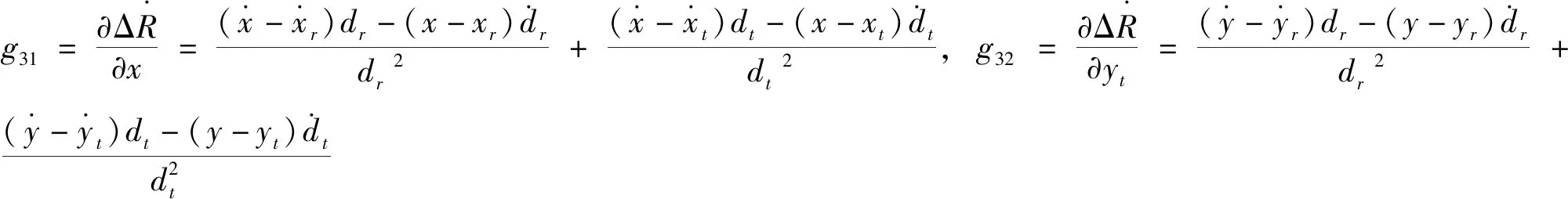
dY=GdX

(13)

式(13)的最小二乘解为

dX=(GTG)-1GTdY

(14)

将式(11)代入得

dX=(GTG)-1GTCdXt

(15)

辐射源位置误差的协方差矩阵为：

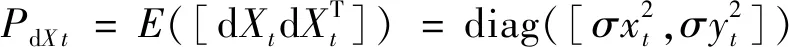
(16)

则目标定位误差的协方差矩阵为：

PdX=E([dXdXT])=[(GTG)-1GTC]

PdXt[(GTG)-1GTC]T

则几何定位精度GDOP为：

(17)

其中trace(·)表示二维方阵求迹运算。

3 仿真分析

在实际定位过程中，所使用的辐射源状态并不准确，与真实的辐射源状态在位置、速度方面会存在一定的误差。假设辐射源的位置误差与速度误差

3.1 DOA-TDOA基线联合定位误差仿真分析

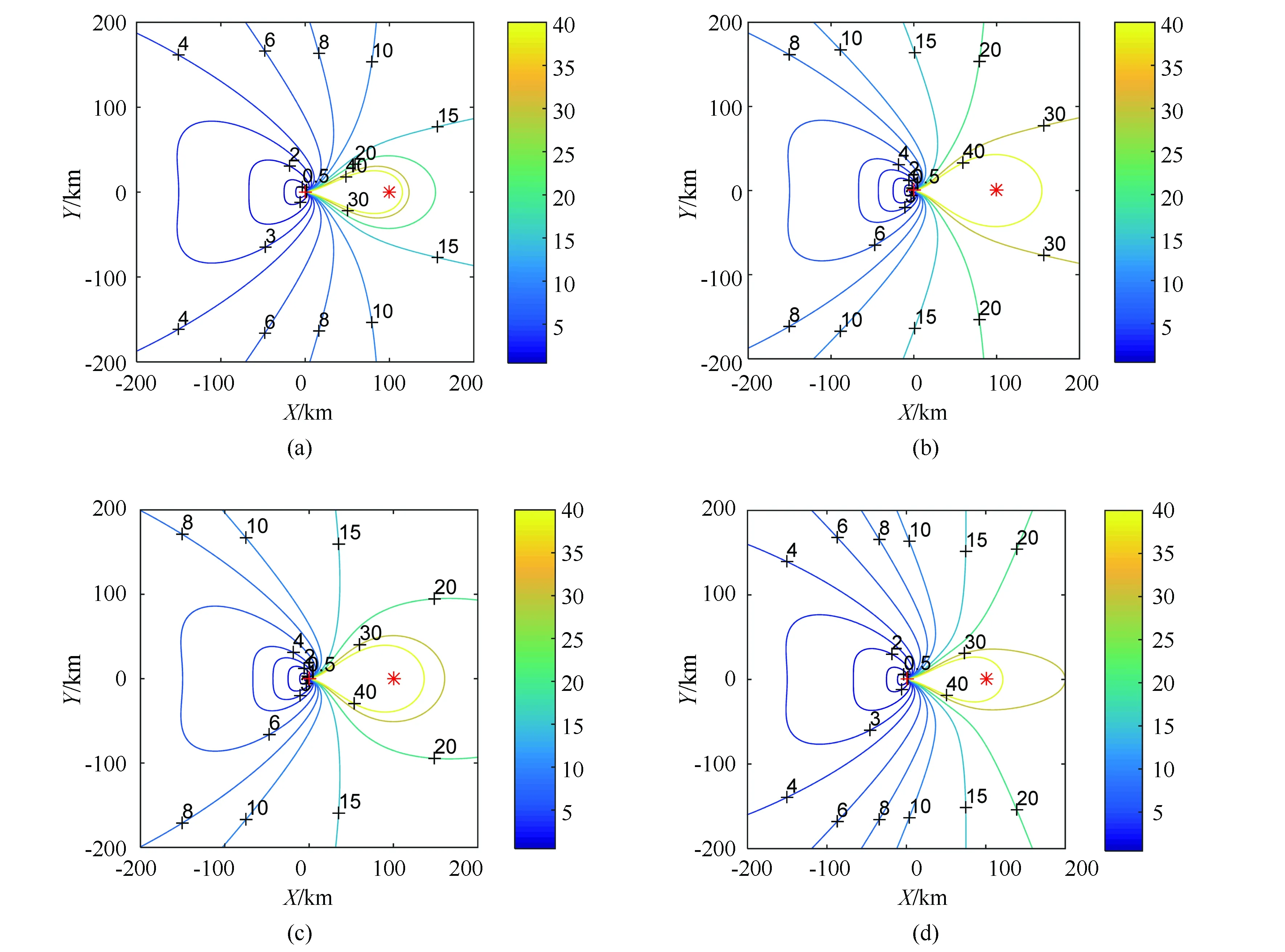
图2 定位误差分布的等高线图

观察DOA-TDOA基线联合定位的GDOP，发现其计算公式里没有速度项，仅与接收站、辐射源、目标的位置及位置不确定有关。仿真计算所用的参数如下：

接收站位于坐标原点，基线长度dtr=100 km，辐射源的初始位置为(0，100)km，位置误差协方差仿真条件如表1所示。除基线长度外，DOA、TDOA的数值均在仿真中实时计算，故未给出具体参数。

表1 辐射源位置误差条件

图2(a)-2(d)是定位误差分布的等高线图，处于同一等高线上位置的定位误差相同。图中红色‘+’表示接收站位置，红色‘*’表示辐射源位置。观察图2(a)可知，等高线呈闭合形式，近似环绕接收站向外扩张且相交于一点。接收站周围等高线稠密且数值较小，辐射源周围等高线稀疏且数值较大，同时接收站与辐射源连线附近区域并无等高线。由图可知，离接收站越近，定位误差越小；离辐射源越近，定位误差越大；当目标出现在接收站与辐射源连线上时，无法对其进行定位。

通过图2(a)与图2(b)的比较，当辐射源位置误差都扩大一倍时，目标定位误差也随之扩大一倍，与公式推导结果一致；对比图2(a)、图2(c)、图2(d)可知，分别增大X轴、Y轴位置误差都会导致目标定位误差增大，且Y轴位置误差增大时，目标定位误差变动更剧烈。

3.2 DOA-TDOA多普勒频移联合定位

在DOA-TDOA多普勒频移联合定位中，由于求解多普勒频移时包含速度项，在该部分仿真时，除了研究辐射源位置误差对GDOP的影响，还需要研究辐射源速度大小、方向以及速度误差对于GDOP的影响。仿真计算所用的参数如下：

接收站位于原点，初始状态向量为[0， 100 m/s， 0， 100 m/s]，目标初始速度为(200 m/s, 200 m/s)，设辐射源的初始状态为[100 km， 100 m/s， 100 km， 100 m/s]，其中辐射源位置误差、速度误差以及收发站与目标相对速度关系的具体参数见表2～表4。由于DOA、TDOA、FDOA的具体数值均在需按照目标、辐射源、接收站的实时状态进行计算，故在此处未给出具体参数。

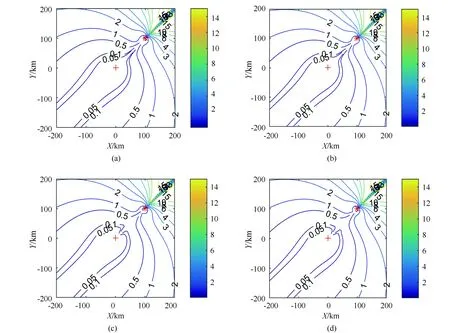
图3 定位误差对比分析图(辐射源位置误差对 GDOP的影响)

仿真一：辐射源位置误差对GDOP的影响

保持基本参数不变，控制辐射源X轴方向和Y轴方向的位置误差，具体参数见表2。

表2 辐射源位置误差条件

观察图3(a)～图3(d)，目标定位误差关于接收站与辐射源连线延长线成轴对称，在接收站一侧的连线延长线附近定位误差较小，在辐射源一侧的连线延长线附近目标定位误差较大，在连线上无法对目标进行定位。目标定位误差关于接收站一侧的连线延长线依次向外扩大。通过图3(a)～图3(d)的对比，在此定位方法中，辐射源位置误差对目标定位误差的影响并不显著。

仿真二：辐射源速度误差对GDOP的影响

保持基本参数不变，控制辐射源X轴方向和Y轴方向的速度误差，具体参数见表3。

表3 辐射源速度误差条件

观察图4(a)和图4(b)，当辐射源X轴方向与Y轴方向速度误差相等时，目标的定位误差关于接收站与辐射源连线延长线呈轴对称，目标定位误差关于辐射源速度误差的分布特征与其关于辐射源位置误差的分布特征相同。观察图4(c)～图4(d)，当辐射源X轴方向与Y轴方向速度误差不同时，目标定位误差的分布便失去了对称性，但总的分布特征仍然是靠近接收站的区域定位误差越小，靠近辐射源的区域定位误差越大。

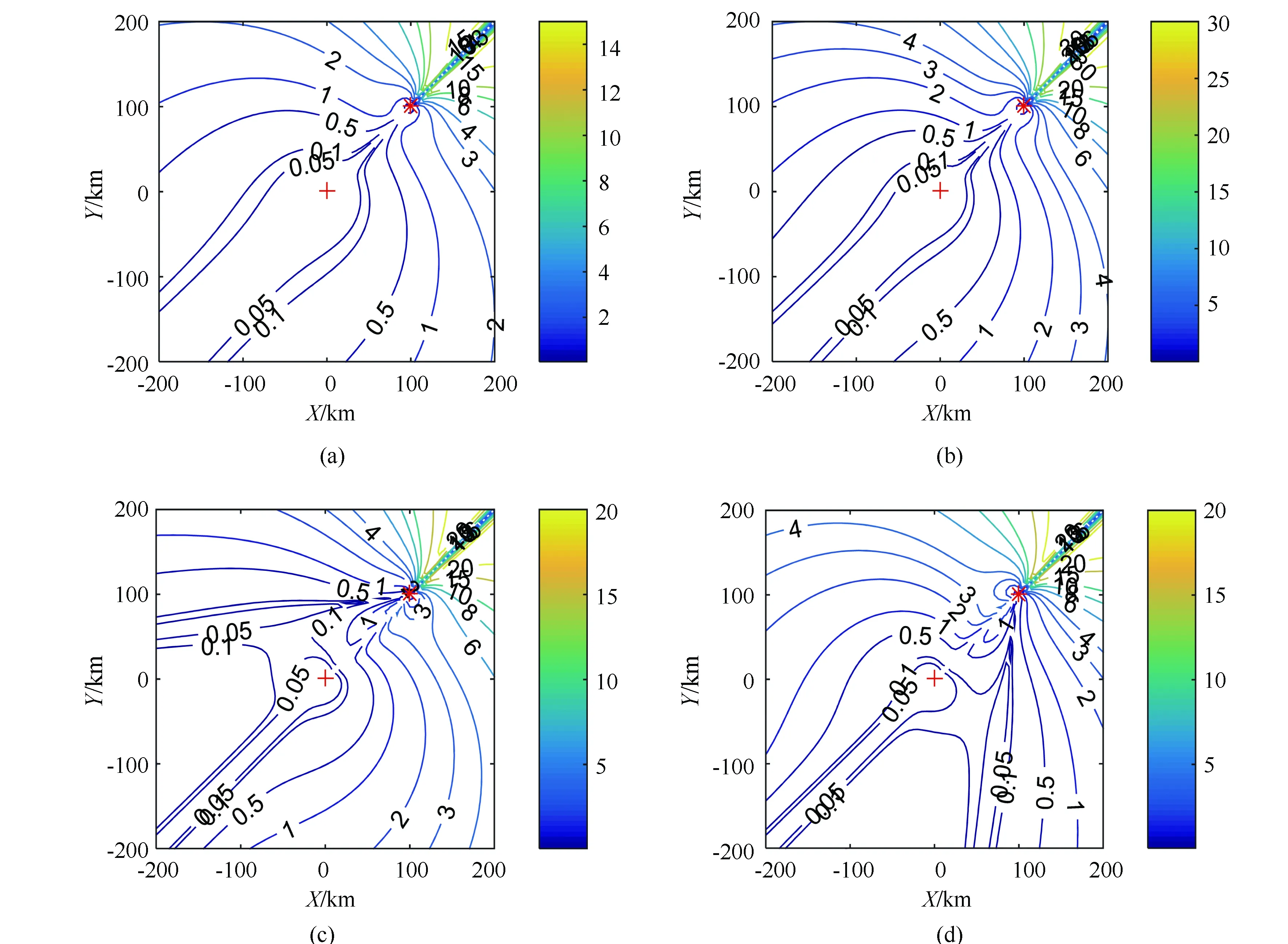
图4 定位误差对比分析图(辐射源速度误差对 GDOP的影响)

仿真三：相对速度对GDOP的影响

保持其它条件不变，分别控制目标、接收站、辐射源的速度，具体仿真条件见表4。

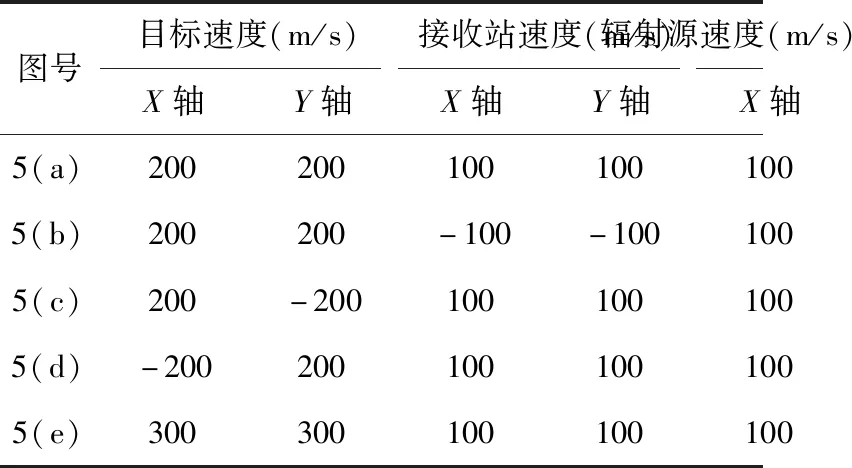
表4 相对速度条件

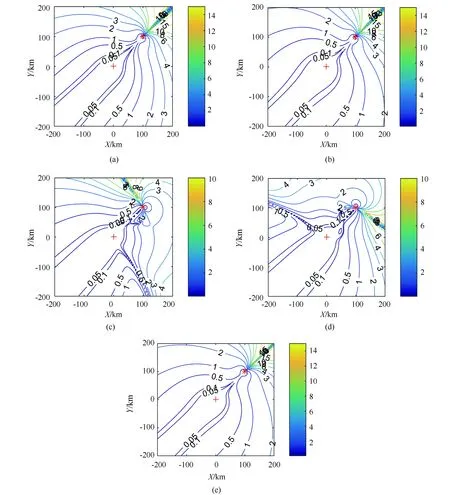
图5 定位误差对比分析图(相对误差对 GDOP的影响)

观察图5(a)、图5(b)，接收站与辐射源之间相向运动或向背运动对目标定位误差的影响不大，其中两者向背运动时，目标定位误差会稍小。对比图5(a)、图5(c)、图5(d)，当目标速度垂直于接收站与辐射源连线时，目标定位误差的分布特性失去对称性。对比图5(a)、图5(e)，当目标速度增大时，目标定位误差会降低。

4 结 语

(1) 目标越靠近辐射源时，目标定位误差越大。因为辐射源位置误差是一定的，目标离辐射源越近，辐射源位置的不确定性就会对两者的相对位置造成影响。同时，此时的几个观测量的较为接近或者数值较小，容易受到辐射源不确定性的影响。综上两点，目标离辐射源越近，借助辐射源对目标进行定位就越困难。

(2) 当目标位于接收站与辐射源连线上时，接收站测得的目标方位角等于辐射源方位角，两路信号的到达时间差近似为0，无法对目标进行定位。

(3) 发现影响目标定位误差的因素较多，辐射源位置误差大小、速度误差大小都会影响目标定位误差的大小，而三者相对速度的方向则会影响目标定位误差的分布，情况较为复杂，缺乏一般性结论，需要具体情况具体分析。