2004-2018年我国狂犬病疫情时间序列分析
谢 渊,刘淑清,董国英,朱武洋
狂犬病是一种由狂犬病病毒引起,以犬、狼、猫等食肉动物为主要传播媒介,以恐水、怕风、进行性瘫痪为主要临床特征的急性和致命性的人兽共患病[1-2]。狂犬病的症状一旦发展,其死亡率几乎为100%,目前该病仍高居甲乙类传染病死亡率首位[3]。狂犬病主要通过动物的咬伤或刮伤进行传播,狂犬病病毒感染中枢神经系统最终导致脑部疾病和死亡[4-5]。所有种类的哺乳动物对狂犬病病毒易感,但狗仍是狂犬病的主要载体且大部分人间狂犬病都由其引起[6-7]。
狂犬病在全球范围内流行,每年导致数万人死亡,而95%以上发生在亚洲和非洲[8],其中印度和中国是报道病例数最多的国家[9]。公元前556年我国首次出现狂犬病病例报道,目前该病仍是非常严重的公共卫生问题。为进一步了解我国狂犬病疫情的分布特征和流行趋势,并对狂犬病疫情进行短期内预测,现利用2004-2018年我国狂犬病发病数据建立季节性时间序列并对其进行分析。
自回归移动平均模型(Autoregressive Integrated Moving Average Model, ARIMA) 即Box-Jenkins模型,一般表现形式为:ARIMA(p,d,q)×(P,D,Q)s。其中p(P)、d(D)、q(Q)分别为非季节性(季节性)的自回归平均阶数、移动平均阶数、差分次数,s则为模型的季节周期[10]。该模型在时间序列分析中应用广泛,对传染病的短期预测具有良好的拟合效果[11-12]。故本研究基于ARIMA模型,对2004-2018年我国狂犬病疫情进行时间序列分析,并对其进行短期预测以期对我国狂犬病的防控提供参考。
1 材料和方法
1.1资料来源 2004-2018年全国狂犬病月发病统计数据来自中国疾病预防控制中心“疾病监测信息报告管理系统”。
1.2 分析方法
1.2.1序列的建立和平稳化 将2004-2017年我国狂犬病月发病数据时间单位定义为年份、季度和月份,而后可得到相应的时间序列曲线图,通过时间序列图观察序列的平稳性,利用SPSS 19.0对不稳定的时间序列数据进行数据转化和差分处理达到序列平稳化的目的[13],并达到以下要求:均数和方差不随时间变化;自相关系数仅与时间间隔相关。
1.2.2模型的识别和定阶 狂犬病疫情呈现季节性变化特征,故可用ARIMA模型进行拟合。ARIMA模型一般表现形式为:ARIMA(p,d,q)×(P,D,Q)s。其中p(P)、d(D)、q(Q)分别为非季节性(季节性)的自回归平均阶数、移动平均阶数、差分次数,s则为模型的季节周期。定阶过程即根据平稳时间序列的自相关图(ACF)和偏自相关图(PACF)初步确定模型参数的过程。通过观察ACF和PACF的截尾或拖尾的情况对模型进行拟合,比较所得到的拟合结果并对其做出相应的调整,初步建立一个或多个可拟合的ARIMA模型。
1.2.3模型的检验和优化 根据平稳的R2、正态化的BIC和平均绝对标准化误差(MASE)等指标对模型的拟合度进行检测评价。同时对模型进行Ljung-Box检验,判断模型残差序列是否为白噪声序列,筛选出通过检验的模型,确定正态化的BIC值最小的为最优模型。
1.2.4模型的验证和评价 以我国2018年1-12月狂犬病月发病数据为验证样本,以平均绝对误差和平均相对误差为评价标准,将最优模型所得的预测结果和实际结果进行比较,评价最优模型的预测精准度。
1.2.5模型的应用 利用最优模型对我国2019年狂犬病疫情进行预测。
2 结 果
2.1序列的建立和平稳化 以2004-2017年我国狂犬病月发病数据建立时间序列图(图1),横轴表示2004年1月-2017年12月时间轴,纵轴表示期间每年月发病数。所建立的时间序列图显示2004-2007年我国狂犬病发病呈现上升趋势,至2007年达到高峰,当年全国报告发病人数达3 300人,而2008-2017年我国狂犬病发病数逐渐下降。图中还显示每年的8-10月发病数可达至高峰,说明8-10月为狂犬病的高发月份。总体而言,2004年1月-2017年12月间,我国狂犬病发病数波动较大,呈现出以年为周期的变化趋势,整体疫情存在明显的季节性变化,由此说明该时间序列为非平稳时间序列。
观察原始序列图发现序列呈现周期性变化规律,且周期为12个月。因此为了获得平稳的时间序列,需对原始序列进行对数转换和差分处理。通过尝试后发现,经自然对数转换、一阶普通差分和一阶季节性差分后可消除原始序列的变化趋势从而使之达到平稳的状态,得到的序列图如图2所示。图2表明差分后时间序列图的长期趋势和季节性变化趋势消失,且数值在零上下波动。此外,观察差分前后的自相关系数和偏自相关系数分析图(图3)发现,仅当k=1和k=12时,自相关系数突破了置信区间,自相关系数和偏自相关系数在k=1后逐渐呈现衰减的趋势且逐渐落入可信区间范围内,故认为此时的时间序列已趋于平稳。

图1 2004-2017我国狂犬病月发病数据时间序列图Fig.1 Time series of monthly incidence data of rabies in China from 2004 to 2017
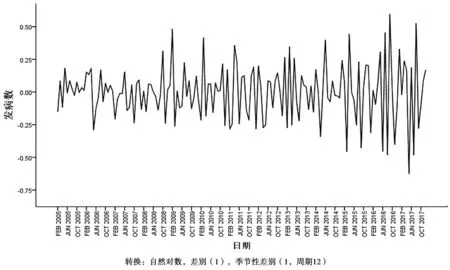
图2 2005-2017年我国狂犬病月发病数据经对数转换、一阶普通差分和一阶季节性差分后序列图Fig.2 Time series of monthly incidence data of rabies after logarithmic transformation, first-order ordinary difference and first-order seasonal difference, 2005-2017
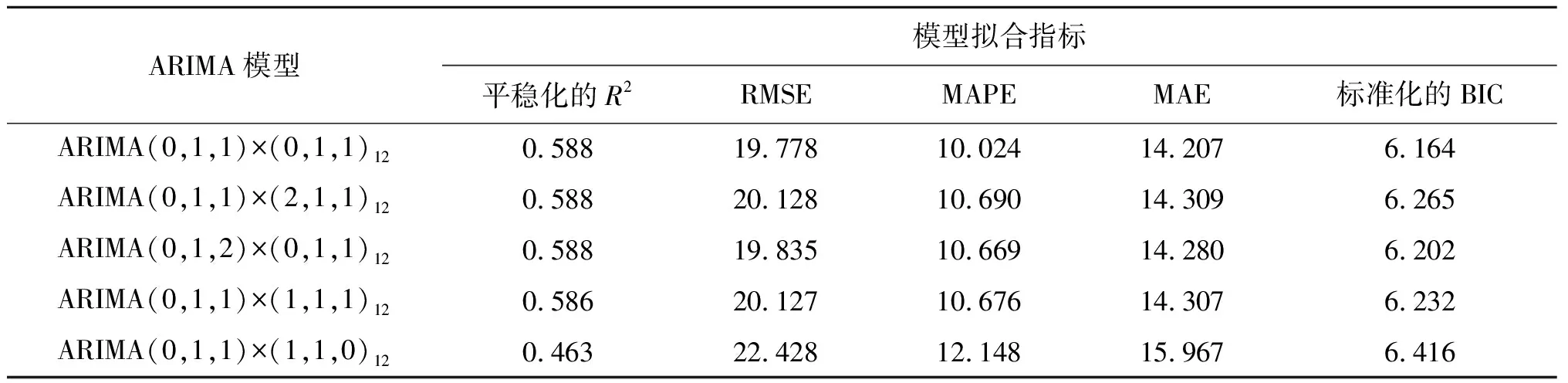
2.2模型的识别和定阶 由于2004-2017年我国狂犬病月发病数呈现出明显的季节性变化趋势,故采用ARIMA乘积季节模型对我国狂犬病疫情进行拟合建模。对原始时间序列进行一阶普通差分和一阶季节性差分后获得平稳时间序列,故可确定d=1,D=1,ARIMA乘积季节模型表现为:ARIMA(p,1,q)×(P,1,Q)12。一般情况下,p、q、P、Q不超过二阶,故对所有符合条件的模型进行筛选。此外,根据对数转换和一阶差分处理后的自相关和偏相关分析图,以正态化的BIC、平均绝对标准化误差、均方根误差和标准化的R2为参考依据,初步筛选出5个拟合度较高的模型,其结果见表1。
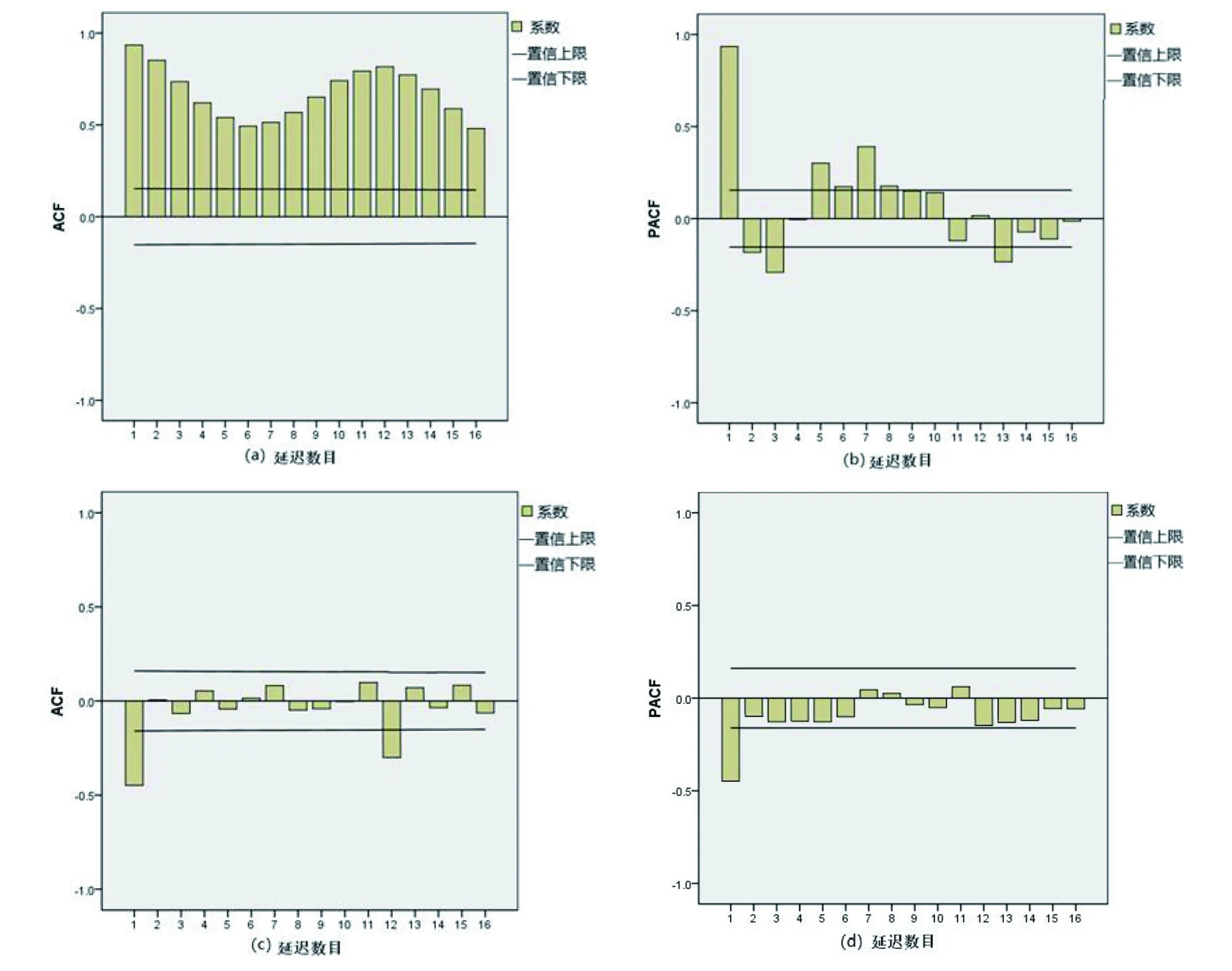
图3a: 差分处理前自相关系数分析图;图3b: 差分处理前偏自相关系数分析图;图3c: 差分处理后自相关系数分析图;图3d: 差分处理后偏自相关系数图Fig.3a: Autocorrelation coefficient (ACF) of monthly rabies incidence time series; Fig.3b: Partial autocorrelation coefficient (PACF) of monthly rabies incidence time series; Fig.3c: Autocorrelation coefficient (ACF) of monthly rabies incidence time series after differential processing; Fig.3d: Partial autocorrelation coefficient (PACF) of monthly rabies incidence time series after differential processing 图3 差分处理前后自相关系数和偏自相关系数分析图Fig.3 Autocorrelation coefficient (ACF) and the partial autocorrelation coefficient (PACF) of monthly rabies incidence time series before (after) differential processing
表1 不同自回归阶数和移动平均阶数ARIMA模型的拟合参数
Tab.1 Fitting parameters of different ARIMA models
ARIMA模型模型拟合指标平稳化的R2RMSEMAPEMAE标准化的BICARIMA(0,1,1)×(0,1,1)120.58819.77810.02414.2076.164ARIMA(0,1,1)×(2,1,1)120.58820.12810.69014.3096.265ARIMA(0,1,2)×(0,1,1)120.58819.83510.66914.2806.202ARIMA(0,1,1)×(1,1,1)120.58620.12710.67614.3076.232ARIMA(0,1,1)×(1,1,0)120.46322.42812.14815.9676.416
注:R2(决定系数),RMSE(均方误差平方根),MAPE(平均绝对误差百分比),MAE(平均绝对误差)
2.3模型的检验和优化 正态化的BIC越小,标准化的R2越大,模型拟合效果越好[14],因此可以确定拟合效果最好的模型为ARIMA(0,1,1)×(0,1,1)12。利用Box-Ljung方法对所获得的最优模型的残差序列进行白噪声检验,检验结果显示最优模型Ljung-Box Q=14.413,自由度为16,P>0.05,无统计学意义,表明该模型的残差序列为白噪声序列。ARIMA(0,1,1)×(0,1,1)12模型的参数估计结果(表2)显示,MA滞后和MA季节性滞后的估计值均有统计学意义(P<0.05)。此外,根据最优模型的残差ACF和PACF分析图(图4)可知,残差ACF和PACF大部分都处于95%置信区间内,表明该残差的分布是随机的,不存在相关性,满足独立性检验。综上所述,获得的ARIMA(0,1,1)×(0,1,1)12模型是有效的且拟合效果较好。
表2 模型ARIMA(0,1,1)×(0,1,1)12的参数估计结果
Tab.2 Parameter estimation result of ARIMA(0,1,1)×(0,1,1)12

参数类别迟滞模型系数t值P值常数0.2900.935-0.3100.757MA滞后10.6810.06410.5950.000MA,季节性滞后10.9940.0910.4750.003季节性差分1
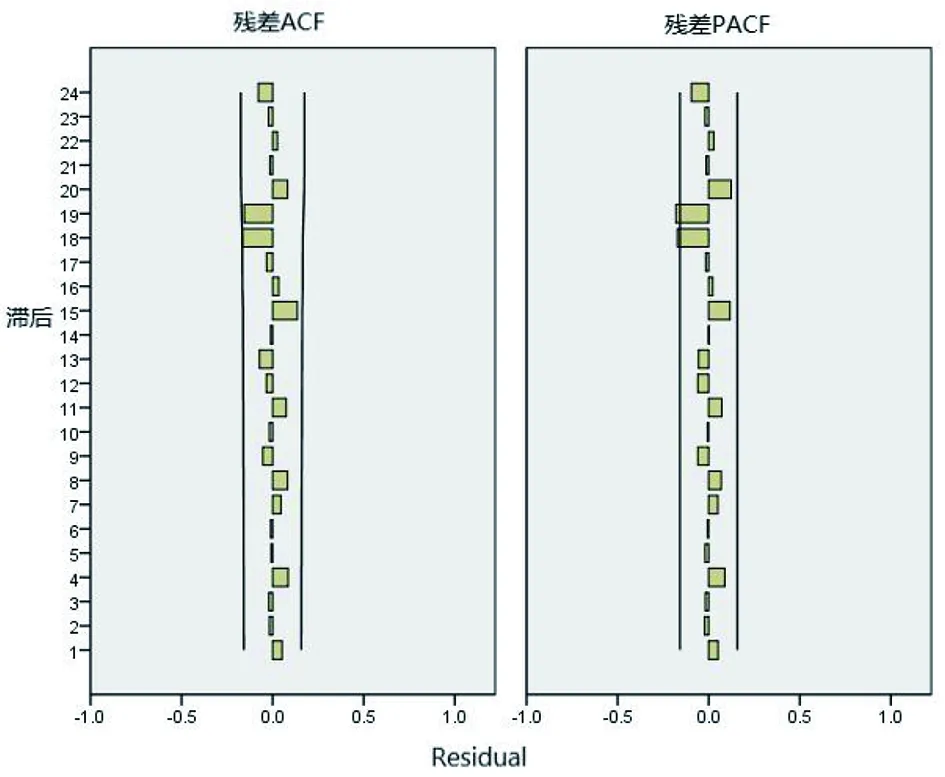
图4 ARIMA(0,1,1)×(0,1,1)12模型残差序列的自相关系数和偏自相关系数图Fig.4 Autocorrelation coefficient and partial autocorrelation coefficient of ARIMA(0,1,1)×(0,1,1)12
2.4 模型的验证和评价
2.4.1回代拟合 将获得的最优模型ARIMA(0,1,1)×(0,1,1)12对2004-2017年的月发病数据进行回代拟合(图5),结果显示拟合值和观测值变化趋势基本一致且观测值一直处于预测可信区间内。
2.4.2模型预测 利用获得的最优模型ARIMA(0,1,1)×(0,1,1)12对2018年我国狂犬病月发病数据进行预测,将预测值与真实值进行比较,结果如表3所示。结果表明预测结果的平均相对误差为14.91%,按预测12个月总发病数据来看,相对误差为0.82%。
表3 2018年我国狂犬病发病预测值和实际值
Tab.3 Predictive and actual values of rabies in China in 2018
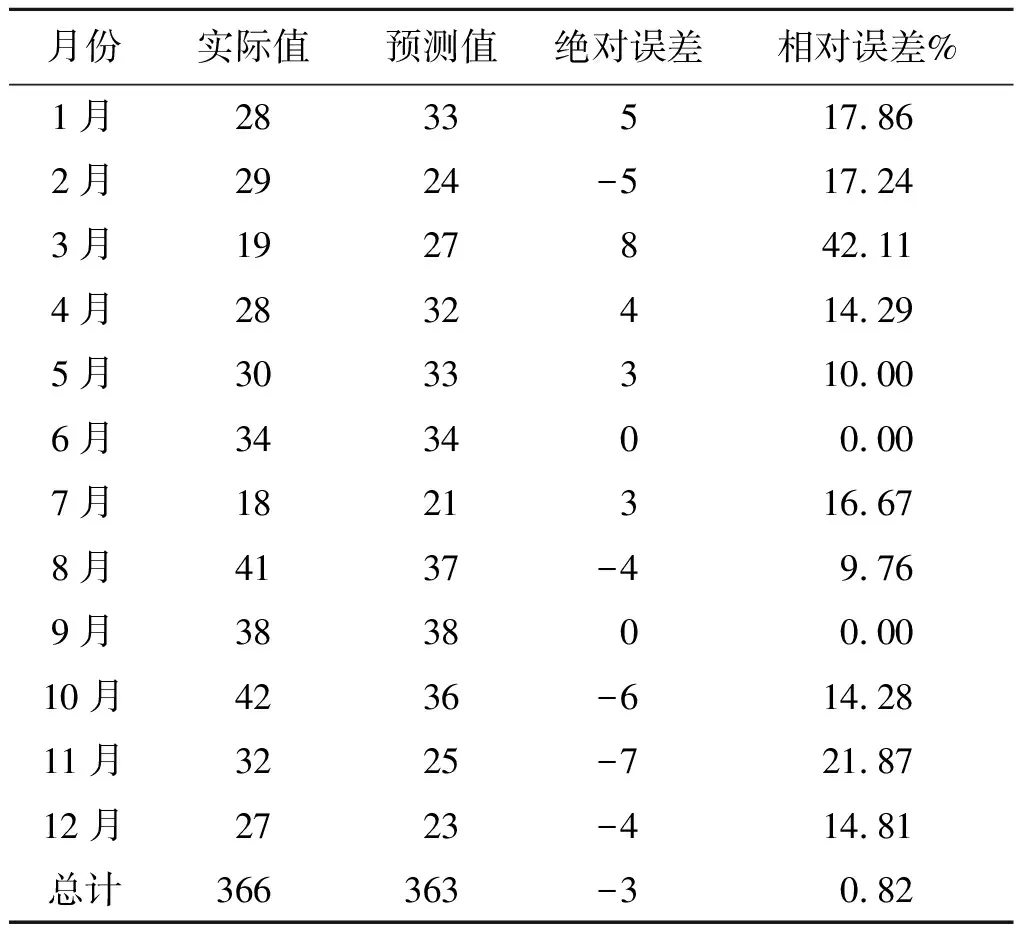
月份实际值预测值绝对误差相对误差%1月2833517.862月2924-517.243月1927842.114月2832414.295月3033310.006月343400.007月1821316.678月4137-49.769月383800.0010月4236-614.2811月3225-721.8712月2723-414.81总计366363-30.82
2.5模型的应用 利用最优模型ARIMA(0,1,1)×(0,1,1)12对我国2019年狂犬病月发病数据进行预测,结果显示,2019年我国狂犬病总发病数预计达208例。
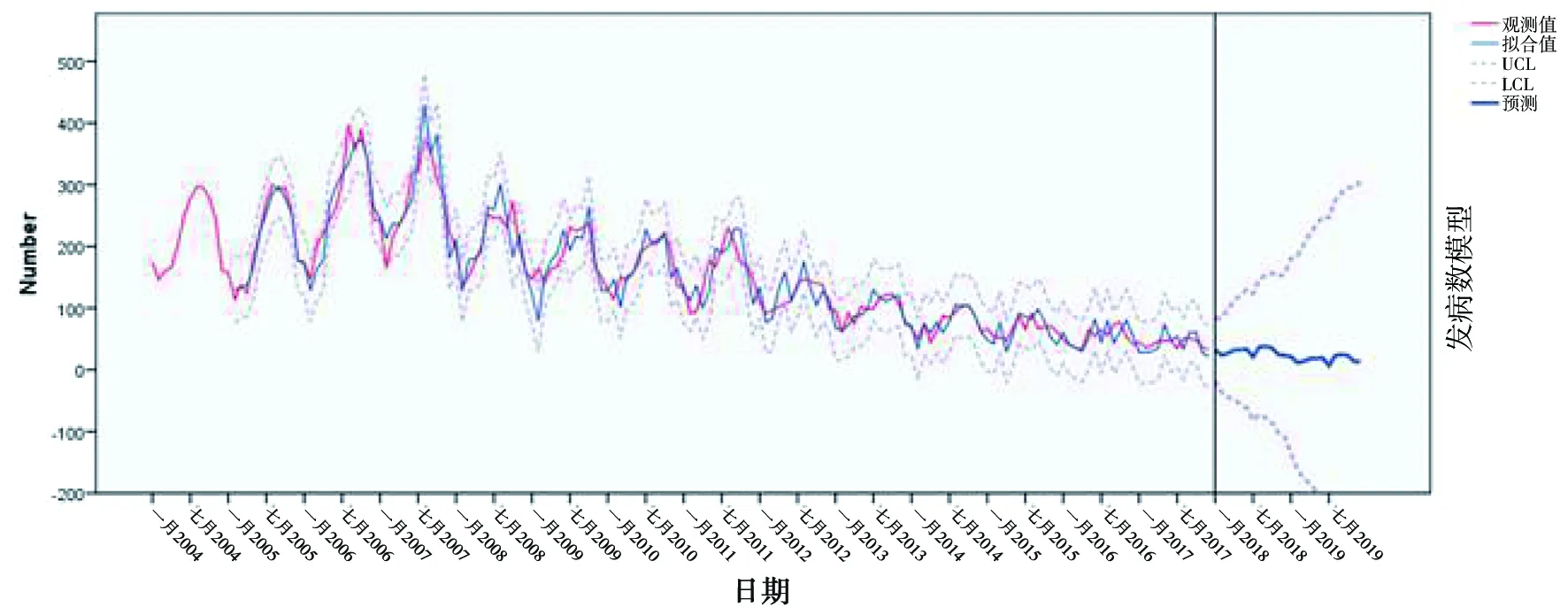
图5 模型ARIMA(0,1,1)×(0,1,1)12回代拟合结果Fig.5 Fitting result of ARIMA(0,1,1)×(0,1,1)12
3 讨 论
狂犬病是一种在全球范围内广泛流行的急性传染病和人兽共患病,全球已有150余个国家深受其害,每年造成大量的经济损失。截至目前,亚洲和非洲仍然是狂犬病高发地区,狂犬病仍在人间、家养动物和野生动物之间循环[15]。我国是继非洲后狂犬病疫情最为严重的国家,自2007年以来,我国狂犬病疫情呈现缓解的趋势,但形势依旧严峻。因此,狂犬病的疫情监测和防控仍是我国传染病防制工作的重点之一。
时间序列分析是一种定量预测的方法,它可将疾病发生的多种影响因素如地理环境和季节环境等综合考虑于时间变量中,分析发病数据随时间变化的规律进而对疾病的发生进行短期内的预测[16]。目前,ARIMA模型是时间序列分析最基础、最常见的方法,该模型不仅可对狂犬病疫情进行预测,也广泛应用于其他传染病的预测分析[17-19]。本研究采用了ARIMA乘积季节模型对我国2004-2018年狂犬病月发病情况进行了时间序列分析,目的在于分析近年来我国狂犬病的流行特征和流行趋势,并对狂犬病的短期流行做出预测。分析结果显示模型预测的我国狂犬病发病趋势和实际值吻合度较高,相对误差较小,表明ARIMA模型可用于我国狂犬病疫情的预测。但由于ARIMA模型是利用历史数据进行统计分析,且疾病的发生还受其他诸多因素的影响,故ARIMA模型只适用于疾病的短期预测[20]。因此,为了对我国狂犬病的疫情进行更加精准的预测,需不断补充新的数据,结合狂犬病发生的其他影响因素,调整模型的参数以适应狂犬病的实际发生情况。
利益冲突:无

