塑料大棚结构的脉动风速与风压时程模拟

姜迎春，白义奎，周东升，王永刚

(沈阳农业大学 a.工程学院；b.水利学院；c.信息与电气工程学院，沈阳 110866)

0 引言

温室是一种特殊形式的农业建筑，除了提供植物生长、生产的基本空间及适宜的温度、湿度环境外，还要承担极端自然灾害(强风、暴雪)所产生的各类荷载作用。随着温室结构的不断发展，温室结构安全问题日益受到重视，相关人员针对风荷载在温室结构设计中的取值问题[1]、温室表面风压分布规律[2-3]及温室承载力等方面[4-5]进行了研究。

近年来发生了多起由于大风导致塑料大棚结构倒塌的工程事故，造成了很大的经济损失[6]。塑料大棚结构属轻型结构，具有自重轻、跨度较大、骨架结构柔而薄、杆件截面小的特点，使得这种结构对风荷载较为敏感。对于塑料大棚结构在时域内进行分析，可以更为精确地掌握塑料大棚结构的风振特性。进行时域分析时需要得到风速的时程样本，即解决风荷载的输入问题。由于目前应用于实际塑料大棚结构的强风作用过程记录还不能普遍实现，采用人工模拟风速时程的方法能有效解决风速时程样本问题。风速时程的模拟主要是针对脉动风速时程而言的，主要采用谐波叠加法和线性滤波法[7-9]。目前，针对超高层建筑[10]、风力发电塔[11]、大跨度桥梁[12]等结构均有风速时程的模拟研究，因此对于风荷载影响明显的塑料大棚结构的风速时程模拟也应进行深入研究。

本文根据塑料大棚的结构特点，对其脉动风场的特性进行研究，给出塑料大棚结构风荷载模拟方法。首先，建立塑料大棚结构模型并给出相关参数；其次，设计数值模拟计算程序，获得脉动风速和脉动风压的时程曲线；最后，将模拟功率谱与目标功率谱进行了对比，变化趋势吻合较好，可为塑料大棚结构动力响应分析提供风荷载模拟输入条件。

1 风荷载模拟方法

(1)

1.1 平均风速

平均风速随高度发生变化，可以通过风剖面来平均风速变化规律可用指数函数表示[14]，即

(2)

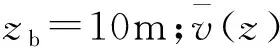
图1 塑料大棚结构脉动风模拟的框架结构图Fig.1 Fluctuating wind simulation of plastic greenhouses structure

1.2 脉动风速

脉动风具有随机性，可用具有零均值的平稳高斯随机过程来表达。脉动风速的特性可用功率谱和相关函数描述。其中，功率谱反映脉动风速中各频率成分对应的能量分布规律；相关函数则反映各点脉动风速之间在时间或空间的相互影响关系。风工程中广泛采用Davenport提出的沿高度不变的风速谱[13]，即脉动风速的自功率谱为

(3)

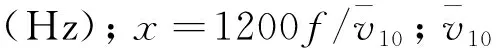
脉动风速的统计特性可用互谱密度函数来描述，互相关函数的值大小表征了空间两点脉动相关程度的强弱。互谱密度矩阵为

(4)

其中，Sii为点i的脉动风的自功率谱；Sij为点i和点j的互功率谱，表示脉动风场的相干性。

互谱密度矩阵中的元素可通过下式求得，即

(i,j=1, 2 ,…,n)

(5)

其中，Coh(f)为相干函数；θ(f)为相位角。

互谱密度与相干函数有如下的关系，即

(6)

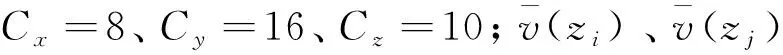
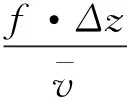
(7)

按照Cholesky分解法，互谱密度矩阵S(f)可分解为

S(f)=H(f)H*(f)T

(8)

其中，H(f)为下三角矩阵；H*(f)T为H(f)的转置共轭矩阵。

脉动风假定为具有零均值的平稳高斯随机过程，采用谐波叠加法[15]将脉动风速vi(t)表示为

cos[2πflt+θjk(fl)+φkl]

(9)

其中，N为脉动风频率采样点数；j为模拟点的个数；Hjk(fl)为上述下三角矩阵中的元素；Δf=(fu-fd)/N为频率增量，fu和fd分别为脉动风截取频率的上限和下限；θjk(fl)为两个不同作用点之间的相位角；φkl为均匀分布在[0,2π]之间的随机数。

对式(9)进行快速FFT变换[16]计算，可得到脉动风速时程vi(t)。

1.3 脉动风压

在已知风速的情况下，可得到顺风向高度处的风压w(z,t)为

(10)

2 仿真实例

2.1 塑料大棚的模型与参数

图2为塑料大棚骨架结构计算模型。其跨度为6.0m，脊高为2.5m；骨架结构共55个节点；风速模拟的时间步长取0.1s，计算时长为100s；频率取值范围为0～1Hz；脉动风频率分割份数N=1024。

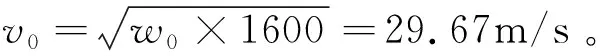
图2 塑料大棚结构示意图Fig.2 Sketch of the plastic greenhouses structure

2.2 模拟结果分析

2.2.1 不同空间点脉动风速时程模拟

采用MatLab 2010a软件编制了仿真程序，在PC机(内核i5-4590 3.3GHz CPU，16G内存，Windows 7 64bit)上进行了模拟。图2中的塑料大棚结构中点1、点2、点6、点11处的脉动风速时程分别如图3中的(a)～(d)所示。从各点时程可知：点1和点2的空间位置相近，模拟的风速时程也相近；点6和点11的空间位置相差较大，则风速时程也有显著差别。4个空间点的风速时程曲线的峰值出现在79s的时刻，此时点6和点11的峰值明显大于点1和点2的峰值。

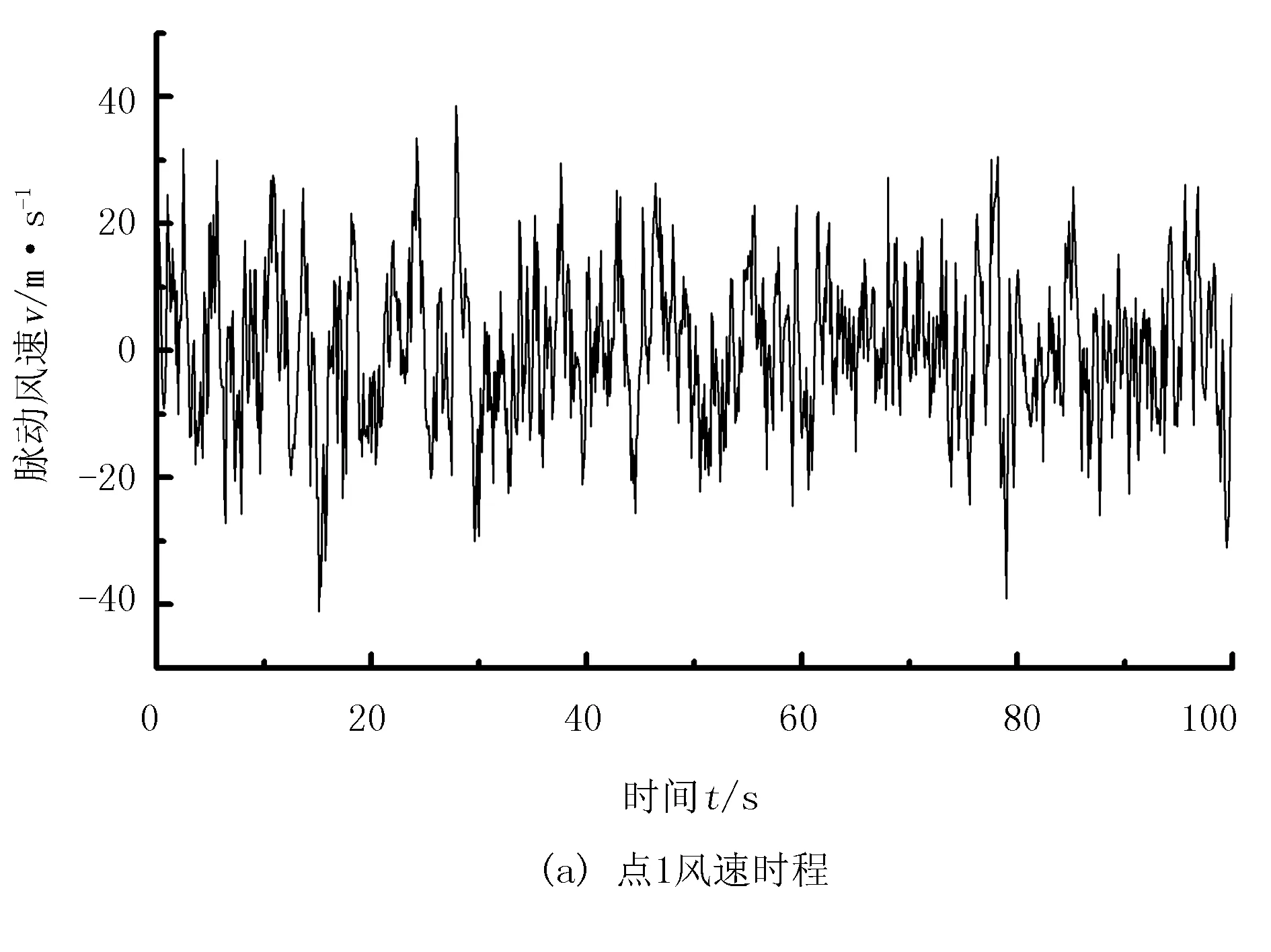
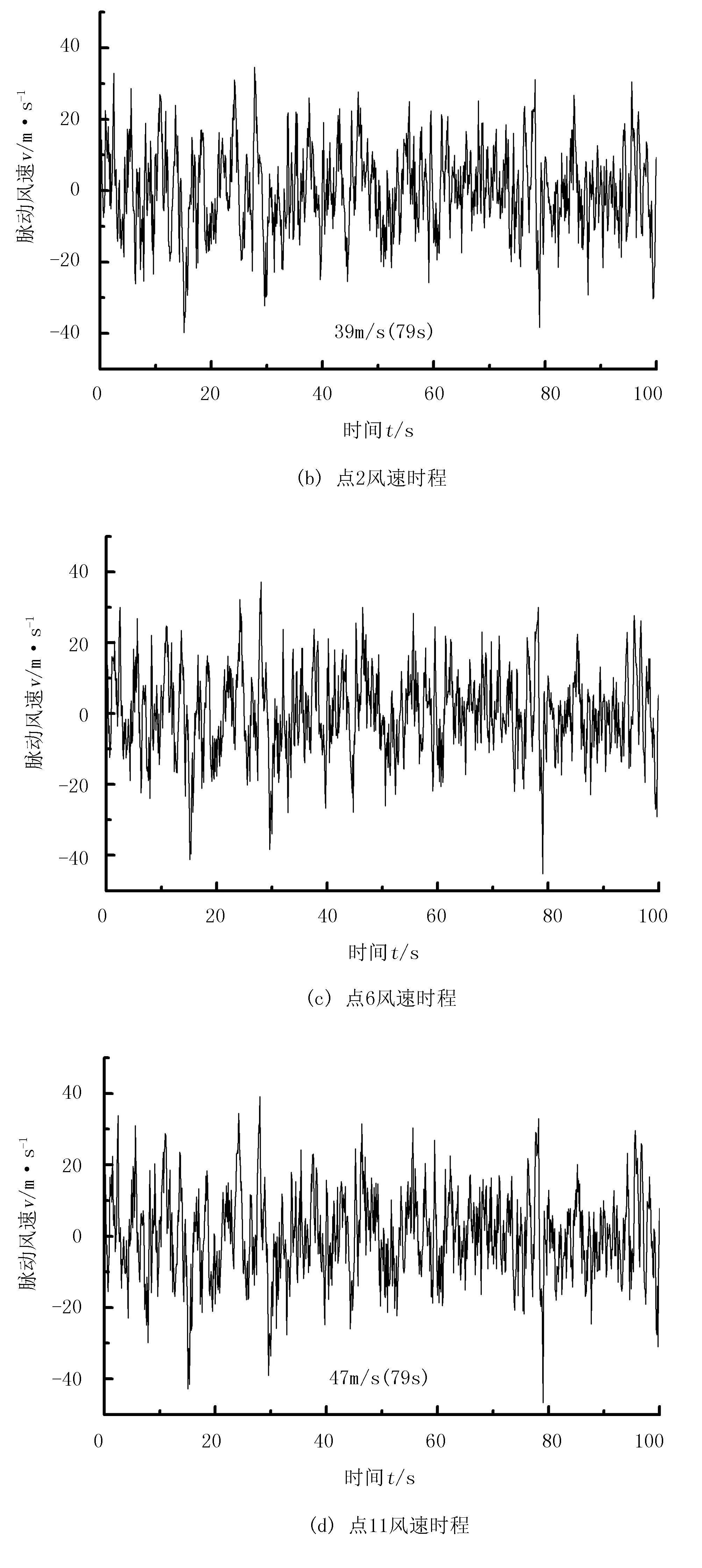
图3 塑料大棚结构不同空间点的脉动风速时程曲线Fig.3 Fluctuating wind speed time history curve in different space points of the plastic greenhouses structure

2.2.2 不同空间点脉动风速功率谱模拟

脉动风速的自功率谱能够反映出模拟风速与实际风速统计特性的相似度。模拟得到的点1、点2、点6、点11的风速功率谱与Davenport脉动风速功率谱对比结果，采用双对数坐标轴形式表示，如图4中的(a)～(d)所示。由图4可见：模拟功率谱的变化趋势与目标功率谱吻合效果较好，塑料大棚结构空间位置不同点的脉动风速时程的模拟结果是可靠的。

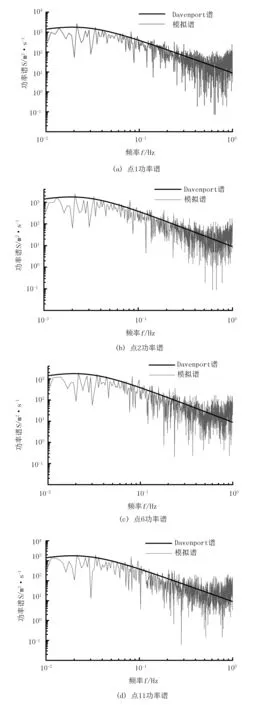
图4 模拟谱与目标谱对比Fig.4 Fluctuating wind power calculation spectrum contrast with target spectrum

2.2.3 不同空间点的相干性比较

图5中的(a)～(d)为空间1点分别与点2、点4、点6和点11的空间相干性的比较，Rmax表示归一化的互相干函数的最大值。由图5可知：点1、点2两个相邻点的风速的相干性最强，其相干性函数最大值Rmax=0.9741；点1和点4的相干函数最大值Rmax=0.9441；点1和点6的相干函数最大值Rmax=0.9150；点1和点11的相干性最弱，其相干性函数最大值Rmax=0.8756。可见，相邻两点风速的相干性较强，随着两点距离的增加，风速的相干性逐渐减弱，符合风场相干性规律。

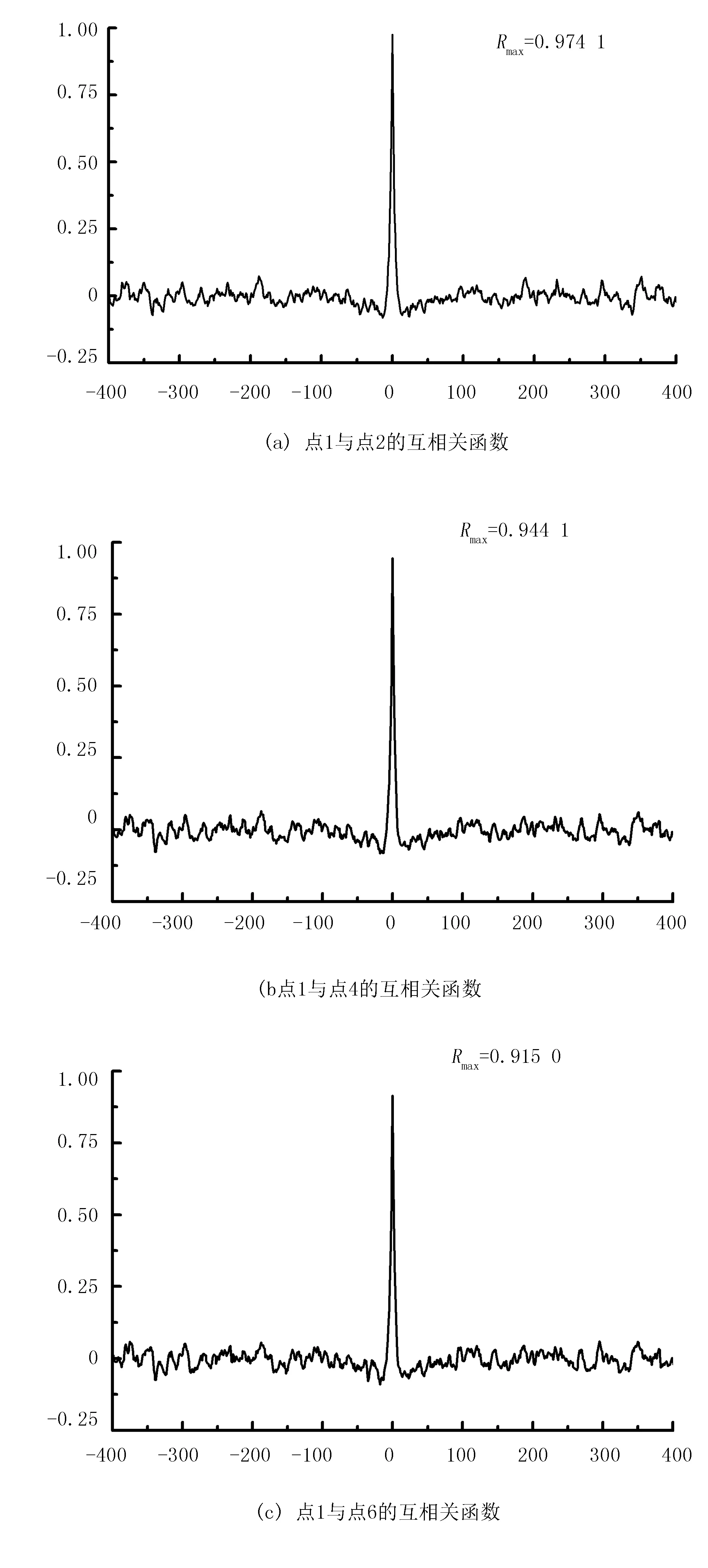
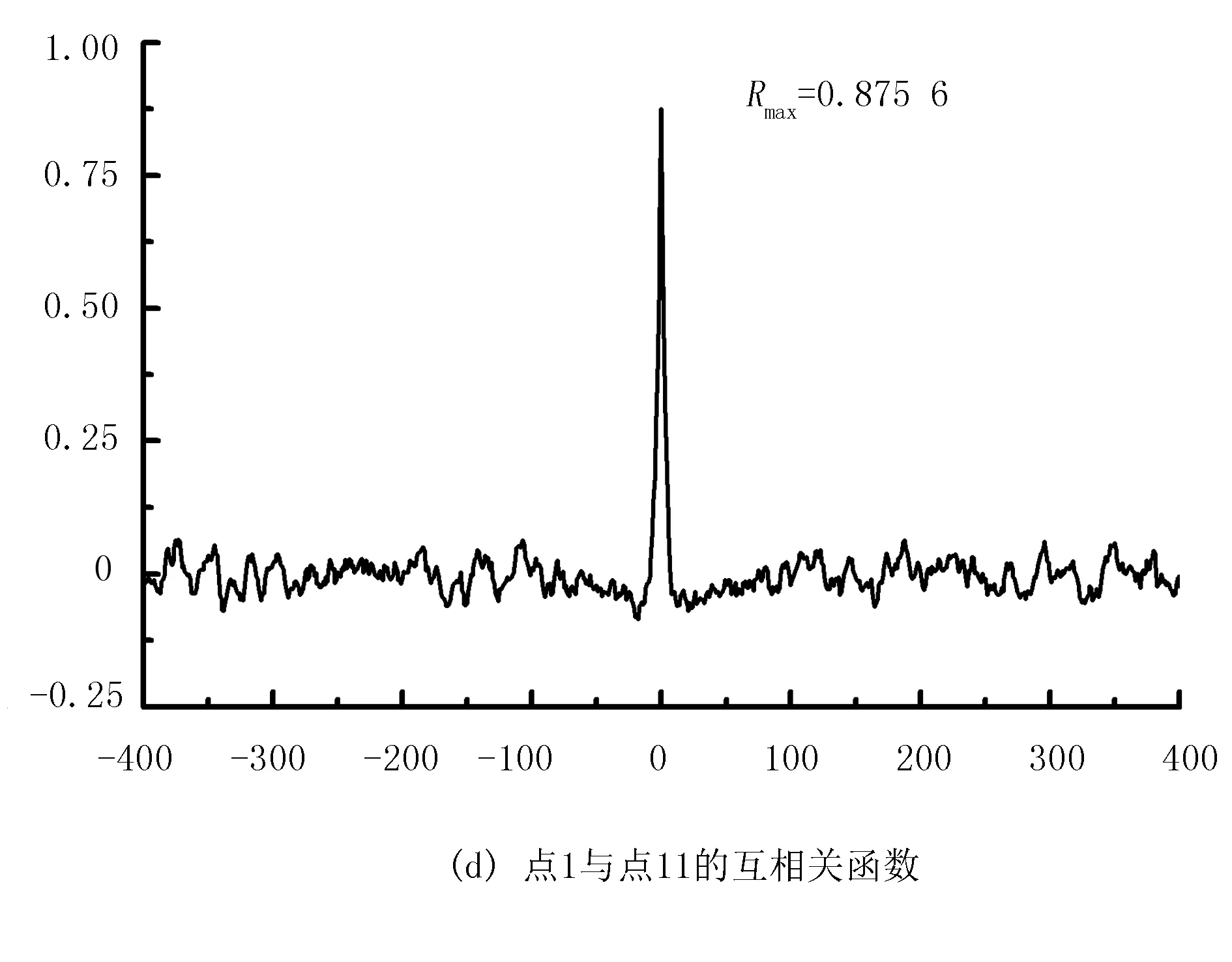
图5 不同点的归一化互相关函数比较Fig.5 The normalized cross correlation function of different differences

2.2.4 不同空间点的脉动风压时程模拟

不同点处的脉动风压时程曲线可由平均风速和脉动风速得到。图6为模拟点2和点11的风压时程曲线。随空间点的变化风压也产生变化，点2在27.8s时出现风压的最大值为2.03kN/m2；点11在28s时出现风压的最大值为2.4kN/m2。脉动风压时程可为研究塑料大棚结构风振响应提供荷载条件。

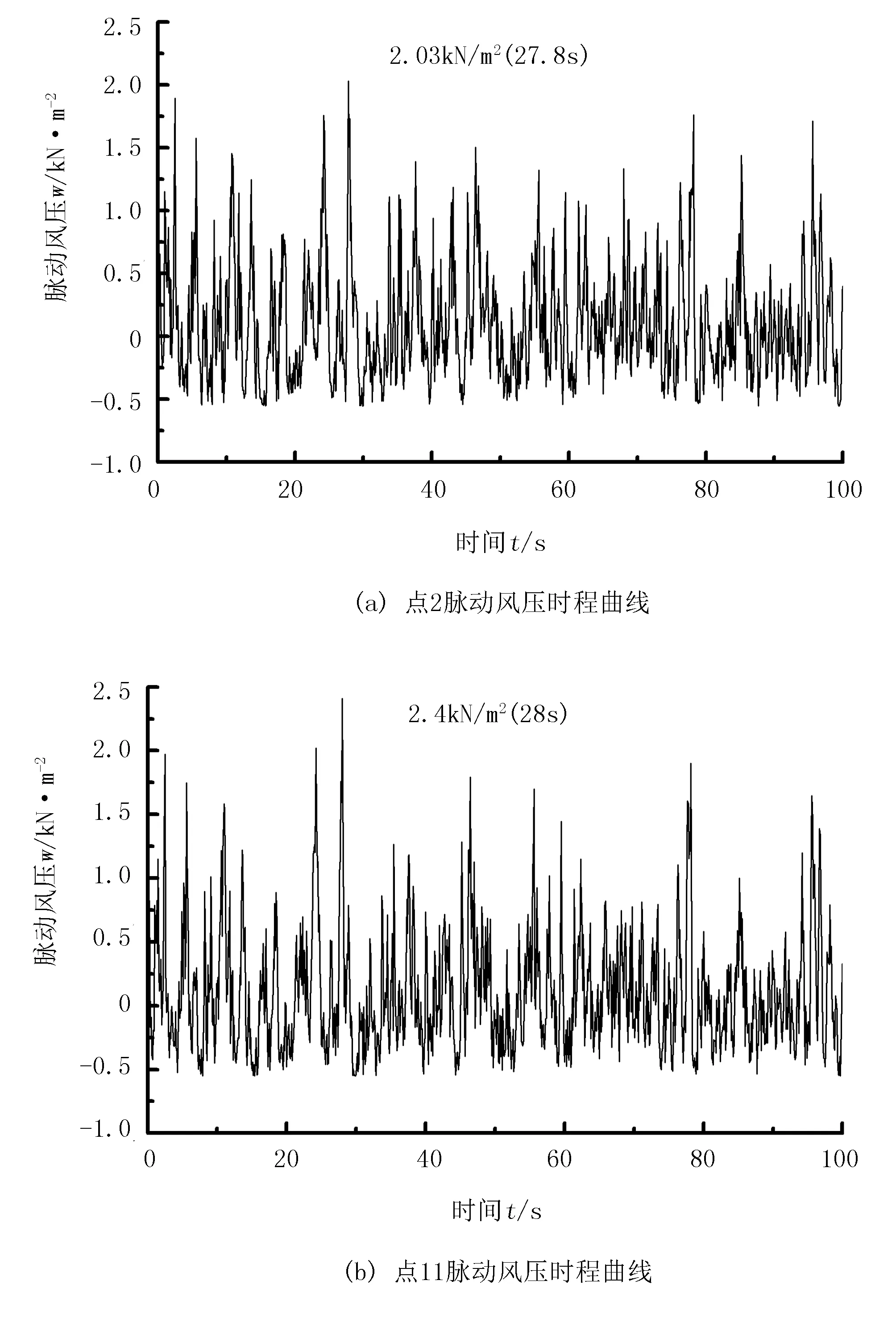
图6 塑料大棚结构不同点的脉动风压时程曲线Fig.6 Fluctuating wind pressure time history curve in different space points of the plastic greenhouses structure

3 结论

采用谐波叠加法对塑料大棚结构空间不同点的脉动风速进行模拟，获得了脉动风速时程曲线。不同空间点的脉动风速峰值出现的时刻相同，但数值相差较大；随着空间位置的增加，风速时程曲线的差异也增加。分别将不同空间点的风速功率谱与Davenport脉动风速功率谱进行对比，结果表明：模拟功率谱与目标功率谱的变化趋势吻合效果较好，表明脉动风速时程的模拟满足精度要求。计算了不同空间位置的相干性，两个相邻点风速的相干性最强，随着两点距离的增加，风速的相干性逐渐减弱，变化规律符合风场的相干性规律。模拟了不同点的脉动风压时程，旨在为研究塑料大棚结构风振响应提供荷载条件。