模糊层次分析法在村镇房屋鉴定中的应用

杨修歌

(河南理工大学 土木工程学院，河南 焦作 454000)

在脱贫攻坚工作决胜的关键期，危房改造工作是保证贫困群众住房有保障的重点。村镇房屋结构形式杂乱，建造随意，大致可分为土坯结构、土木结构、砖木结构、砖混结构、框架结构等5类。由于村镇房屋大多为自建房屋，监管力度不足，房屋没有设计图纸，全凭工匠的个人经验建造。因此，村镇房屋的安全鉴定工作常采用定性的方式去评判，全凭鉴定人员的专业素质，存在严重的弊端，鉴定的结果往往存在严重的主观性，不能反映房屋真实的使用现状。

结构试验评价方法可通过现场或室内试验检验和判定构件实际的性能，根据试验和分析结果判定结构挠度、裂缝宽度或承载力等是否满足要求，此方法虽然可精确分析，但需要非常专业的检测人员，而且检测和设备投入方面花费较大，不符合村镇经济现状[1]。现提出使用模糊层次分析法，将评价过程中的非定量构件作定量分析是对人们的主观判断作客观描述的一种有效办法，在村镇房屋鉴定工作取得较好的效果。

1 建筑物评价指标体系构建

由于村镇房屋布局较为简单，根据其房屋不同的结构形式，可以将建筑物从下到上划分为基础构件、竖向承重构件、上部构件，在此基础上建立3个一级评估指标。

一级评估指标：A1下部构件,A2竖向承重构件,A3上部构件

由于每个一级评估指标又有影响自身安全性能的因素，继而在一级评估指标的基础上建立更加全面的2级评估指标，见表1。

表1村镇房屋评价体系
Table1Rural housing evaluation system

一级评估指标二级评估指标 A1下部构件 x11周围环境 x12基础沉降 x13基础承载力 A2竖向承重构件 x21墙体裂缝 x22墙体倾斜 x23柱子损坏 A3上部构件 x31梁损坏 x32屋顶损坏 x33防水损坏

2 模糊层次分析法

模糊层次分析法(FAHP)及计算过程层次分析法(AHP)是20世纪70年代美国T.L.Saaty教授提出的，是一种定性与定量相结合的多准则决策方法，更是一种确定指标权重行之有效的方法[2]。该方法克服了由于因素多而人们难以判断的缺点,迎合了人们的思维习惯,使得评价更加简单和清楚,是种定量与定性相结合的决策方法,将专业人员的经验给予量化,从多角度各层次对各个指标进行综合评价。

2.1 建立评价集

根据《危险房屋鉴定标准》(JGJ125—2016)鉴定结果的划分准则[3]，A级表示房屋基本完好；B级表示房屋结构或个别承重构件有轻微损伤，经一般修理后可继续使用；C级表示房屋部分承重构件受到损伤，局部出现险情，需经加固改造后方可继续使用；D级表示房屋大部分承重构件受到严重破坏，整体出现险情或濒临坍塌，一般需拆除重建。建立建筑物的评价集V。

V={Vk}=

{V1安全，V2较安全，V3较危险，V4危险}

2.2 构造判断矩阵

判断各级评估指标的相对重要性，并构建判断矩阵A：

(1)

矩阵中xij表示xi对xj的相对重要性数值(i,j=1,2,…,n)，xij的取值依照表1进行。

表2判断矩阵标度表[4]
Table2Scale table of judgment matrix

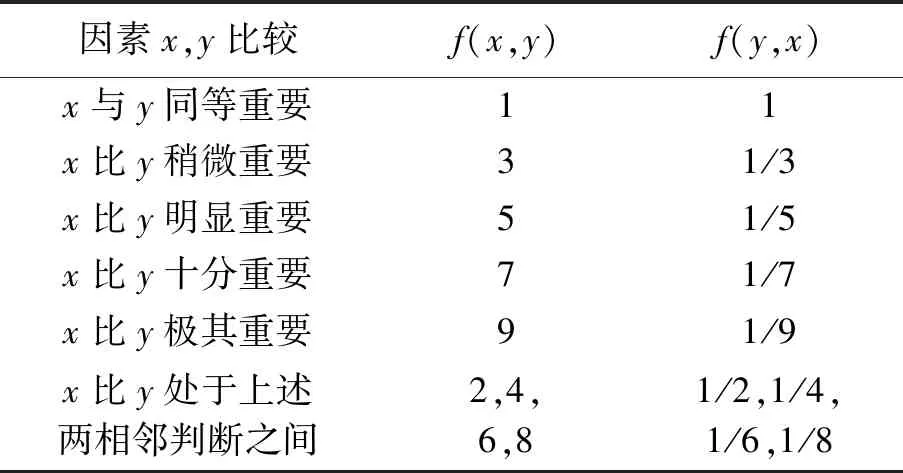
因素x,y比较f(x,y)f(y,x)x与y同等重要11x比y稍微重要31/3x比y明显重要51/5x比y十分重要71/7x比y极其重要91/9x比y处于上述两相邻判断之间2,4,6,81/2,1/4,1/6,1/8

2.3 确定各级权重

根据判断矩阵A，求出最大特征根对应的所对应的特征向量，特征向量即为各级因素的权重。判断矩阵特征向量计算方法有方根法与和积法[5]。现用和积法，步骤如下：

i,j=1,2,…,n

(2)列正规化的判断矩阵按行相加λmax=

Wi则为特征向量

(4)计算判断矩阵的最大特征根

2.4 判断矩阵的一致性检验

在村镇房屋的安全评价中，影响建筑物安全性的因素较多。同时，人对事物的认识也存在一定的模糊性和主观性，需要对判断矩阵的逻辑性进行检验。

CI=(λmax-n)/(n-1)

CR=CI/RI

表3平均随机一致性指标RI[6]
Table3Mean random consistency indexRI

nRI102030.5840.9051.1261.2471.3281.41

当计算的一致性比率CR<0.1时，判断矩阵被认为满足一致性要求，并计算对应于判断矩阵的最大特征值向量以获得权重向量。如果一致性检查不符合要求，则需要修正判断矩阵，直到计算一致性比率满足要求为止。

建立各个层次判断矩阵，用和积法计算其特征性向量，依据层次分析法计算各级指标权重及一致性检验,见表4～表7。

2.5 隶属函数的建立

根据文献[7]，建立合适村镇房屋的隶属度函数。对于定量型评判指标可以利用隶属函数获得评价项目对应不同安全等级的隶属度。对于地基承载力这类评估指标采用“越大越好”型的隶属度函数，而对于墙体裂缝这类评估指标采用“越小越好”型的隶属度函数。

表4一级指标A判断矩阵和参数计算
Table4First-level indexAjudgment matrix and parameter calculation

AA1A2A3WA111/51/30.106A25130.634A331/310.261

λmax=3.036，CI=0.018，CR=0.03<0.1，则一级指标A判断矩阵满足一致性检验。

表5A1下的二级指标判断矩阵和参数计算
Table5Judgment matrix and parameter calculation of secondary index underA1

A1x11x12x13W1x11131/50.193x121/311/70.083x135710.723

λmax=3.067，CI=0.034，CR=0.06<0.1，则二级指标A1判断矩阵满足一致性检验。

表6A2下的二级指标判断矩阵和参数计算
Table6Judgment matrix and parameter calculation of secondary index underA2

A2A21x22x23W2x2111/51/30.106x225130.634x2331/310.261

λmax=3.036，CI=0.018，CR=0.03<0.1，则二级指标A2判断矩阵满足一致性检验。

表7A3下的二级指标判断矩阵和参数计算
Table7Judgment matrix and parameter calculation of secondary index underA3

A3x31x32x33W3x311560.707x321/5130.201x331/61/310.092

λmax=3.096，CI=0.048，CR=0.09<0.1，则二级指标A3判断矩阵满足一致性检验。

对于定性型评价指标需要依据评判标准对现场检测结果进行评判，用“符合”“基本符合”“既符合又不符合”“基本不符合”和“不符合”来评判，为了能够定量表述这些语言而形成评价向量，用1、0.75、0.5、0.25和0来表述以上评判结果。

2.6 评价矩阵的建立

在实际测试结果的基础上，根据每一个因素的特点选用合适的隶属函数，代入隶属函数得到单因素在评价集V上对应每一个安全等级的隶属度，构成单因素评价向量。然后将单因素评价向量综合起来构成因素集的评价Ri矩阵。

(2)

其中：rijk为第i个因素中第j个子因素aij在评价集V上对应的隶属度。

2.7 模糊综合评价

根据模糊综合评价中权重与各级指标对应评价矩阵的合成法则，从底层评价指标逐步向上进行模糊合成，逐步完成目标的模糊综合评价。

Bi=WigRi=

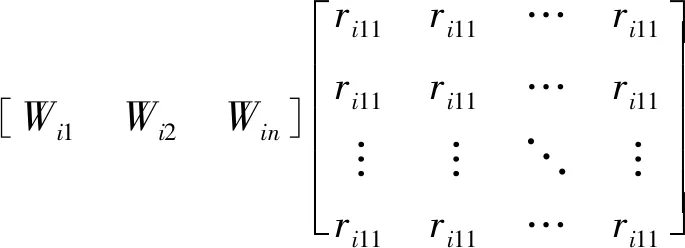
(3)

(4)

B=WgR

(5)

B为模糊综合评价结果，W为特征向量，R为评价矩阵。

3 应用实例

目前在对驻马店确山县进行房屋安全鉴定工作中，以某一村镇民居为例，采取上述方法进行安全性评估。根据现场检测与理论计算得到的评价矩阵以及由层次分析法确定的评价指标的权重，按照公式(2)～(5)对该民居的现状进行评价。

依据现场鉴定人员检测和查看，发现屋顶防水老化，楼板出现多条细微裂缝。据此建立评价矩阵，如下：

二级指标综合评估：

B1=W1gR1=(0 1 0 0)

B2=W2gR2=(0 0.75 0.25 0)

B3=W3gR3=(0 0.58 0.397 0.023)

综合评判：

B=WgR=(0 0.732 0.262 0.001)

根据模糊综合评价结果见图1，该民居安全等级为B级，存在轻微损伤，经一般修理后可继续使用。根据评价向量的结果来看，该民居整体状况良好，屋顶防水存在损伤，需要对该部位进行有针对性的修缮。

模糊层次分析法将定性与定量结合，能够将既有房屋的安全状态进行安全合理的判断，具有可操行，易于推广使用。

4 结论

(1)对村镇房屋结构形式的复杂多样，建立通用的安全评估体系，较全面的评估房屋的使用现状。

图1 模糊综合评价结果Fig 1 Fuzzy comprehensive evaluation results

(2)模糊层次分析法将定性与定量结合，实际操作的层面来讲简单易行，对鉴定人员的专业水平要求不高，评估结果较为真实地反映了既有房屋的安全状态，从而可为房屋安全管理和决策提供依据。