柔性太阳翼叠层电池弯曲适应性仿真与设计
许京荆 韦祎 陈萌炯 马聚沙

摘要:航天器在轨进、出地影时,基于复合结构柔性基板的柔性太阳翼叠层电池在高、低温交变作用下会产生热弯曲变形。针对这一问题,采用有限元建模仿真,分析由太阳电池、盖片胶和抗辐照玻璃盖片组成的叠层电池的弯曲适应性,计算不同结构尺寸、不同叠层材料参数的叠层电池在跨中弯曲载荷下的最大应力。借助响应面技术研究设计变量与复合结构性能之间的关系,采用目标驱动优化分析,获得理想的结构尺寸参数。结果表明:叠层电池的宏观力学性能取决于微观不同叠层材料的组合方式;等效弹性模量不是定值,而是与叠层材料的参数有关;弯曲工况的失效模式取决于电池单体的最大拉应力,而不是宏观表征的整体弯曲强度。
关键词:柔性太阳翼; 叠层电池; 弯曲; 应力; 有限元
中图分类号:V214.11; TB115.1
文献标志码:B
Bending adaptability simulation and design of
solar cell integrated cover of flexible solar array
XU Jingjing, WEI Yi, CHEN Mengjiong, MA Jusha
(College of Mechanical Engineering and Automation, Shanghai University, Shanghai 200072, China)
Abstract:
During the illumination-shadow period of orbit, the cell integrated cover based on the composite flexible substrates of the flexible solar array produces bending thermal deformation under alternating high and low temperature. As to this problem, the flexural adaptability of cell integrated cover consisting of solar cell, adhesive cover and irradiation resistant glass cover, is analyzed using finite element modeling and simulation. The maximum stresses of the cell integrated cover with different structural sizes and different laminated material parameters under mid-span bending loads are calculated. The relationships between design variables and performance of composite structures are studied by response surface methodology. The dimension parameters of the structure are obtained using target-driven optimization analysis. The results show that the macro-mechanical properties of the cell integrated cover depend on the combination of different micro-stacked materials; the equivalent elasticity modulus is not a fixed value, but it is related to the parameters of laminated materials; the failure modes under bending conditions depend on the maximum tensile stress of the cell monomer rather than the overall bending strength as macroscopically characterized.
Key words:
flexible solar array; cell integrated cover; bending; stress; finite element
收稿日期:2019-06-19
修回日期:2019-07-01
作者简介:
许京荆(1970—),女,浙江东阳人,博士,副教授,研究方向为有限元数值分析,(E-mail)xjj125@shu.edu.cn
0 引 言
柔性太阳翼质量功率比高、收拢体积小,在航天器发射体积或质量受限的特殊应用领域中的地位不可替代,例如大面积空间电站、空间站轨道舱、超高功率大型卫星等均适合配备柔性太阳翼。[1-2]我国在研和国外主流的低地球轨道(low earth orbit, LEO)柔性太陽翼电池均采用柔性基板粘贴刚性叠层(光照面粘贴抗辐照玻璃盖片)的结构形式[3],其在轨进、出地影时,复合结构柔性基板在高、低温交变作用下会产生以弯曲形式为主的热变形[4]。
据相关报道,哈勃望远镜卷压型柔性太阳翼在1990年发射入轨后的工作校验期间出现过太阳翼弯曲挠度过大、太阳翼局部供电损失的故障[5],后经地面试验与仿真分析,确定故障是由柔性太阳翼低刚度非对称几何结构的热失配造成基板弯曲过载所致的,太阳翼局部供电损失是由于叠层电池受基板变形影响发生非预期的碎裂而引起部分供电子电路开路所致的。类似的叠层电池碎裂导致太阳翼供电失效的案例,美国地球资源卫星Landsat-2和Landsat- 4也曾先后出现过。[6]
柔性太阳翼在轨弯曲过载引起广泛关注后,研究人员开始在设计阶段寻求一种快速高效的设计方法,对太阳翼温度、热变形和各部分的弯曲适应性进行直观分析。随着计算机的发展,CAE有限元仿真分析以计算精度高、复杂形状适应性强、分析效率高等优点被广泛采用。ZIMBELMAN等[7]仿真研究LEO空间环境下太阳翼在收拢-展开工况下的温度场分布;THOMTON等[8]仿真分析宏观温度梯度及其变化,研究太阳翼温度变化引起弯曲变形导致热颤的机理;丁延卫等[9]和张燕娜等[10]从基板设计角度出发,对太阳翼基板的热变形开展适应性分析与结构优化设计。
本文从叠层电池设计出发,以LEO柔性太阳阵用叠层电池为研究对象,采用有限元建模仿真结合力学试验的方法,开展叠层电池抗弯曲性能分析和结构设计优化,获取叠层电池的等效材料参数、建立有限元分析模型,并得到优化的叠层电池结构尺寸参数。
1 叠层电池力学性能参数确定
叠层电池由锗衬底太阳电池封装抗辐照掺铈石英玻璃构成,其复合结构主要包括锗衬底3J-GaAs太阳电池(电池单体中锗衬底厚度占比为85%)、硅胶和掺铈石英玻璃。[11]
锗为立方晶系的單晶体材料。用正交各向异性材料的主轴坐标系表示应力分量和应变分量,弹性应力-应变关系由广义胡克定律确定,即εm=
Cm
σm。在单晶材料的3个主轴方向上,材料的弹性特性相同,应力-应变关系矩阵为
Cm=
1E-νE-νE000
-νE1E-νE000
-νE-νE1E0000001G0000001G0000001G
(1)
式中:E为材料主轴方向的弹性模量,MPa;ν为泊松比;G为剪切模量,MPa。单晶立方晶系各向异性材料通常给出[100]、[110]和[111]方向的弹性模量E100 ,E110 和E111 (叠层电池弯曲特性测试和分析时需结合实际情况确定具体参数,太阳电池锗片划片方向不同时材料弹性模量取值不同)。确定弹性模量和泊松比后可得到剪切模量G,
1G=4Ex-2-2νE
(2)
式中:Ex表示弹性模量E100 、E110 和E111 ,MPa。
采用DMA Q800动态热机械分析仪开展太阳电池锗衬底三点弯曲弹性模量测定试验。锗片试样件规格为30.0 mm×5.0 mm×0.20 mm,试样制备按太阳电池划片方向分为水平方向[1 10]、垂直方向[110]、+45°方向[100]和-45°方向[010]。根据应力-应变数据拟合,得到水平方向的弹性模量平均值为E1 10 =1.33×105 MPa,垂直方向的弹性模量平均值为E110 =1.38×105 MPa,水平与垂直方向的弹性模量相差不大,均值为1.35×105 MPa;与水平方向夹角45°方向的弹性模量平均值为E100 =1.05×105 MPa。实测的水平与垂直方向都与材料主方向成45°,而45°测试方向为材料主轴方向,计算得到剪切模量G=6.36×104 MPa。
抗辐照掺铈石英玻璃为脆性材料,各向同性材质,试样规格为30.0 mm×10.0 mm×0.125 mm,试样制备后进行4组三点弯曲试验。根据应力-应变数据拟合,得到弹性模量均值为8.25×104 MPa。
2 叠层电池有限元建模
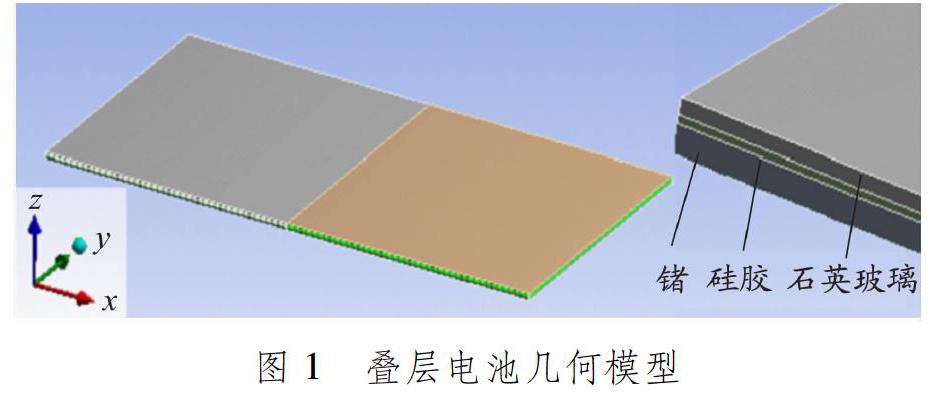
采用ANSYS建立仿真模型,按照初步设计结果设置模型尺寸。叠层电池总尺寸为20.0 mm×10.0 mm×0.29 mm,其中:太阳电池单体为锗,厚度为0.15 mm;中 间为硅胶,厚度为0.02 mm;顶部为石英玻璃,厚度为0.12 mm。叠层电池的几何模型见图1。
电池单体主轴取45°方向,材料本构关系采用正交各向异性弹性模型,弹性模量E100 =1.05×105MPa(三点弯曲测试均值),泊松比ν=0.27,计算剪切模量G=6.36×104 MPa;玻璃和硅胶为各向同性弹性模型。叠层电池材料力学参数见表1。
模型采用三维实体-壳单元,单元大小为0.14 mm,对叠层电池几何模型进行网格划分,见图2。网格划分后节点总数为42 340个,单元总数为31 104个。
3 模型适用性分析
借助试件弯曲试验,比对仿真结果,开展模型适用性分析。
叠层电池三点弯曲试验载荷示意见图3,试验照片见图4,应力-应变测试结果见图5。试样跨距为20.0 mm,宽度为10.0 mm,总厚度为0.29mm,最大负荷F=0.877 N,对应跨中最大挠度t=0.26 mm,宏观抗弯强度为31.4 MPa,弹性模量为2.86×104 MPa。
参考实际试验加载的边界条件,对叠层电池模型进行有限元仿真。根据最大挠度,在z方向施加0.26 mm位移,两端简支,允许绕y轴转动。对比最终仿真结果与试验结果,分析模型的适用性。叠层电池位移加载和最终输出结果见图6~15。
仿真结果显示:叠层电池整体最大变形为0.256 mm; 叠层电池跨中平均挠度为0.256 mm;计算获得的叠层电池反作用力为0.896 N,试验值为0.877 N,二者误差为2.17%;叠层电池总体等效应力为77.98 MPa;太阳电池单体最大拉应力为80.38 MPa; 玻璃最大主应力为45.91 MPa;硅胶等效应力为0.08 MPa; 叠层电池跨中截平面最大主应
力平均值为29.06 MPa。在叠层电池中心位置沿厚度方向设置一条路径,并给出叠层电池跨中中心路径上的线性化正应力,电池单体侧拉应力最大值为32.70 MPa,玻璃侧压应力最大值为-32.70 MPa,与试验弯曲强度31.40 MPa接近。随着试件厚度由0增大到0.29 mm,太阳电池单体的应力从最大拉应力80.38 MPa线性变化到最大压应力-75.3 MPa,硅胶的应力很小。
由小样试件弯曲试验结果与仿真结果的对比可知:小样实测最大负荷为0.877 N,与仿真最大负荷0.896 N的误差为2.17%;小样实测宏观抗弯强度为31.40 MPa,与仿真电池单体/玻璃抗弯强度32.70 MPa 的误差为4.14%。因此,模型仿真结果与实测结果接近,可用于叠层电池结构优化设计。
4 叠层电池结构设计优化
在获得叠层电池复合结构材料主要力学参数与仿真模型后,开展叠层电池结构优化设计,主要考虑太阳电池长度、宽度和厚度,尺寸规格参数选取见表2。按表2设计规格建立有限元数值模型,对叠层电池进行仿真分析。
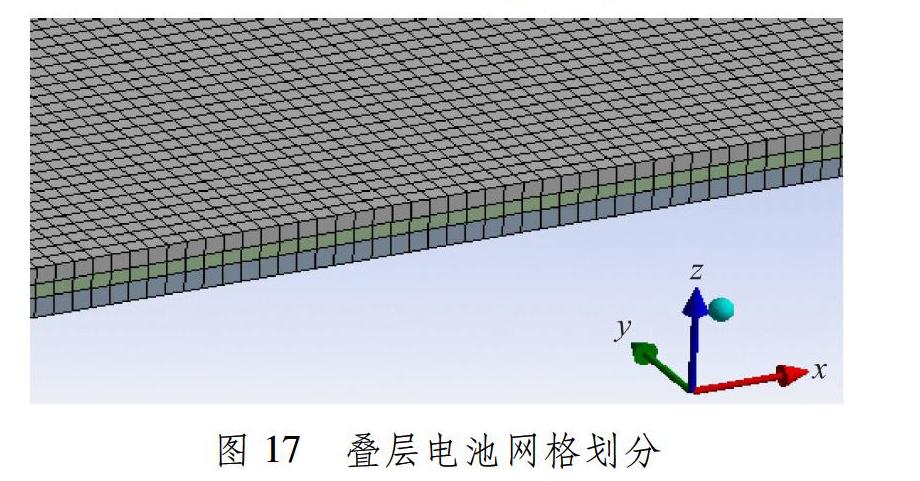
各规格试件几何模型和网格划分方法同前文。规格1电池板尺寸为40.0 mm×30.0 mm×0.36 mm;3层材料中太阳电池单体厚度为0.14 mm,中间硅胶厚度为0.10 mm,顶部石英玻璃厚度为0.12 mm,其三维几何模型见图16。其他规格试件网格划分均相似。在数值模拟过程中,电池单体取主轴方向为0°,材料本构关系采用正交各向异性弹性模型,主轴弹性模量取E100 =1.05×105 MPa(三点弯曲测试平均值),泊松比ν=0.27,计算剪切模量G=6.36 ×104 MPa。玻璃和硅胶为各向同性弹性模型,弹性模量和泊松比的数据取自表1。采用三维实体-壳单元,单元大小为0.12 mm,对叠层电池几何模型进行网格划分,见图17,网格划分节点总数为336 340个,单元总数为250 500个。
根据太阳翼设计技术要求,设置叠层电池跨中承载力为2.396 7 N,对4种规格试件的正面(玻璃面)弯曲进行分析,结果汇总见表3。
分析结果显示,在4种规格的试件中,规格38.3 mm ×31.3 mm×0.39 mm的试件许用承载力最大。叠层电池的宏观力学性能取决于微观不同叠层材料的组合方式,等效弹性模量与叠层材料的参数有关,不是定值。弯曲工况下叠层材料失效取决于最薄弱环节,即某电池单体处,其弯曲失效取决于电池单体的最大拉应力,而不是宏观表征的整体弯曲强度。这一点可由规格38.3 mm×31.3 mm×0.39mm试件的强度和刚度要大于规格40.0 mm×30.0 mm×0.39 mm试件的强度和刚度证实:在同等载荷的情况下,后者最大弯曲应力应该更小,而实际却相反。所以,用整体弯曲强度作为结构失效的评判准则是不合适的。
另外,对4种规格的叠层电池跨中承载进行正、反面(太阳电池面)弯曲分析,得到如下结果。
(1)叠层电池的失效取决于叠层结构和加载方式,实质是由于电池单体或玻璃材料的失效引起的。由于厚度不同,电池单体和玻璃失效的可能性都存在,如规格40.0 mm×30.0 mm×0.34 mm试件玻璃面加载与规格40.0 mm×30.0 mm×0.39 mm试件太阳电池面加载都是电池单体先达到许用拉应力,而规格40.0 mm×30.0 mm×0.34 mm试件太阳电池面加载是玻璃先达到许用拉应力。
(2)当仅考虑拉伸失效时,太阳电池面加载的许用承载力高于玻璃面加载的许用承载力。
(3)依据叠层电池的宏观性能评定其失效行为或者其强度和刚度行为不合适。同样电池规格,正、反面加载得到的弹性模量和弯曲强度不同:受硅胶层厚度的影响,规格40.0 mm×30.0 mm×0.34 mm试件玻璃面加载的弹性模量为2.06×104 MPa,太阳电池面加载的弹性模量为1.92×104 MPa,相差1.07倍; 规格40.0 mm×30.0 mm×0.39 mm試件玻璃面加载的弹性模量为1.87×104 MPa,太阳电池面加载的弹性模量为1.66×104 MPa,相差1.13倍。
(4)可以根据仿真数据推算叠层电池的抗弯强度,如规格40.0 mm×30.0 mm×0.34 mm试件,玻璃面加载的抗弯强度为41.0 MPa×3=123.0 MPa,太阳电池面加载的抗弯强度为46.5 MPa×3=139.5 MPa;规 格40.0 mm×30.0 mm×0.39 mm试件,玻璃面加载的抗弯强度为28.6 MPa×3=85.8 MPa,太阳电池面加载的抗弯强度为44.0 MPa×3=132.0 MPa。
为获得叠层电池具体尺寸更详尽的相关力学性能特征,基于前面给定规格的叠层电池结构布局,以各层厚度、长度和宽度为设计变量,以满足跨中弯曲强度设计要求为目标,建立参数化模型,通过试验设计技术和响应面法研究设计变量与叠层电池结构性能之间的关系,采用目标驱动优化分析(ANSYS中的Workbench GDO模块)获得最佳的叠层电池抗弯结构,强度和尺寸约束范围见表4。考虑跨中弯曲的结构优化,强度约束条件根据许用应力设置。
确定初始计算的叠层电池结构参数,将叠层电池的长度、宽度和各层厚度作为设计变量,指定电池单体最大拉应力、玻璃最大主应力、胶层等效应力和等效弹性模量为输出变量,采用试验设计方法确定45组样本进行仿真计算,基于响应面技术得到设计变量与叠层电池的结构性能之间的关系和最佳的叠层电池抗弯结构。采用目标驱动算法计算,优化分析结果设置长度为40.0 mm,宽度为30.0 mm,总厚度为0.36 mm,各层需要满足强度指标。筛选优化方案,确定叠层电池长度为38.6 mm,宽度为32.3 mm,长宽比为1.2,单体电池厚度为0.23 mm,玻璃厚度为0.06 mm,硅胶厚度为0.02 mm,总厚度为0.31mm,电池单体最大拉应力为91 MPa,承载力为4.6 N,单位宽度承载力为0.144 N/mm,总变形为0.986 mm。
5 结束语
由LEO柔性太阳阵用叠层太阳电池抗弯曲设计和有限元建模仿真分析可知,通过引入计算机辅助有限元仿真,可高效分析叠层太阳电池不同现行尺寸结构的力学性能,改进薄弱环节、优化设计。本文建立一种LEO柔性太阳翼叠层电池有限元分析模型,并得到在设计限定条件下叠层电池抗弯性能优化后的具体结构尺寸参数,为柔性太阳翼叠层电池设计提供参考。
参考文献:
[1]
闻新, 纪龙, 朱诗嘉. 航天器太阳电池阵列的发展历程[J]. 中国航天, 2011(12): 23-27.
[2]JONES P A,SPENCE B R. Spacecraft solar array technology trend[J]. IEEE Aerospace and Electronic Systems Magazine, 2011, 26(8): 17-28.DOI: 10.1109/MAES.2011.5980605.
[3]于辉, 孙彦铮, 金海雯. 空间站柔性太阳翼电池电路部分设计初探[J]. 电源技术, 2013, 37(3): 395-397. DOI: 10.3969/j.issn.1002-087X.2013.03.017.
[4]赵志萍, 赵阳东. 大面积太阳翼国外发展研究[J]. 沈阳航空航天大学学报, 2014, 31(3): 39- 44. DOI: 10.3969/j.issn.2095-1248.2014.03.008.
[5]MUROZONO M,THORNTON E A. Buckling and quasistatic thermal-structural response of asymmetric rolled-up solar array[J]. Journal of Spacecraft and Rockets, 1998, 35(2): 147-155. DOI: 10.2514/2.3322.
[6]冯伟泉. 归因于空间环境的航天器故障与异常[J]. 航天器环境工程, 2011, 28(4): 375-389.
[7]ZIMBELMAN D F,WELCH R V, BORN G H. Optimal temperature estimation for modeling thermal elastic shock disturbance torque[J]. Journal of Spacecraft and Rockets, 1991, 28(4): 448- 456. DOI: 10.2514/3.26265.
[8]THOMTON E A,KIM Y A. Thermal induced bending vibration of a flexible rolled-up solar array[J]. Journal of Spacecraft and Rockets, 1993, 30(4): 438- 448. DOI: 10.2514/3.25550.
[9]丁延卫, 王晓耕, 张立华, 等. 碳纤维/铝蜂窝太阳翼基板热变形分析[J]. 航天器工程, 2009, 18(4): 44- 48. DOI: 10.3969/j.issn.1673-8748.2009.04.008.
[10]張燕娜, 赵泓滨. 太阳电池阵基板结构优化设计[J]. 空间电子技术, 2018, 15(2): 49-53. DOI: 10.3969/j.issn.1674-7135.2018.02.008.
[11]马世俊. 卫星电源技术[M]. 北京: 中国宇航出版社, 2001: 142-184.

