基于混沌量子粒子群BP算法的研究

何晓云，许江淳，陈文绪

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

0 引言

近年来,反向传播(back propagation，BP)算法已经成为机器学习理论中应用较为广泛的网络之一[1]。该算法采用误差反向传播的负梯度下降法，具有较好的非线性函数、自组织能力和泛化能力的特点，为良好预测能力奠定了基础。但BP算法在预测中存在过度拟合[2]、预测精度不高的问题，当拟合精度越高，预测准确率就越低，即泛化能力差。其主要原因是：传统的BP算法每次训练的权值、阈值都不一样，存在随机性；然而，权值和阈值对于BP神经网络的预测能力有很大的影响[3]。为了解决这一问题，国内外许多研究者提出了改进的方法。例如：Srivastava N[4]证明了加入随机噪声的数据集会使神经网络的拟合性能变差，从而可提高泛化能力；防止对网络学习过度是更有效的方法，即在样本数据中添加正则项。王林[5]针对BP算法的权值和阈值随机化、容易陷入局部收敛的特点，设计了一种优化BP神经网络的自适应差分进化算法，避免了部分过拟合现象，但增大了算法的复杂度。

以上研究者提出的成果对于改进BP算法泛化能力的力度不大，导致BP算法预测模型在应用时出现其他问题[6]。因此，本文提出了一种基于混沌量子粒子群优化的BP(chaotic quantum particle swarm optimization BP，CQPSO-BP)算法。量子粒子群优化算法是用混沌序列来初始化种群的初始角[7]，针对粒子群算法的早熟收敛，引入了变异操作，提高了全局优化能力，从而优化BP神经网络的权值、阈值。然后将它与BP算法结合，形成一种新的算法——混沌量子粒子群BP算法。最后，通过与改进的附加动量法和BP神经网络作对比，利用不同的数据集进行预测试验，将准确率、均方误差(mean square error，MSE)、均方百分比误差(mean square percent error，MSPE)作为评价指标[8]。试验结果表明：CQPSO-BP算法在预测精度、收敛速度、准确率等方面，相对于传统的BP神经网络和改进的附加动量法等算法有较明显的优势。

1 BP神经网络

BP神经网络是一种多层馈型网络[9]，主要依靠输入信号的正向传播和误差的反向传播，不断调试网络的权值和阈值，达到优化网络的目的。训练方法采用的是最速下降法traingd。

全局误差函数为[9]：

(1)

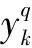
1.1 BP网络的学习过程

①网络初始化。设置BP网络神经元之间的连接权值Wij、Wjk，确定网络输入层节点n个、隐含层节点数l个、输出层节点数m个，以及隐含层和输出层的阈值α[a1,a2,…,al]和b[b1,b2,…,bm]。

②计算隐含层的输出。

(2)

式中：f为激励函数；xi为输入变量。

③计算输出层的输出。

(3)

④更新权值。

ωij(t+1)=ωij(t)+η[(1-β)D(t)+

βD(t-1)]i=1,2,…,n

(4)

ωjk(t+1)=ωjk(t)+η[(1-β)D′(t)+βD′(t-1)]

(5)

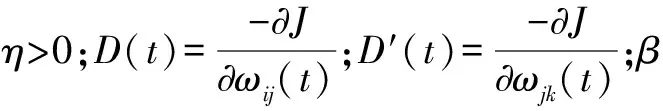
⑤更新阈值。

(6)

bk(t+1)=bk(t)+(yk-ok)

(7)

⑥判断网络训练的误差是否达到要求。若它达到期望的要求或设置的学习次数已用完，就结束网络的训练；否则，返回步骤②。

1.2 动量因子的优化算法

传统的BP神经网络存在收敛速度慢的问题。这主要是因为优化权值时，只根据某一时刻的负梯度方向进行修正，没有考虑以前的修正经验。这里引入了动量因子的方法。当权值陷入局部最小值时，会产生一个继续向前运动的正向斜率。附加动量法的改进不仅考虑了误差在梯度方向的作用[10]，还考虑了误差曲面变化的趋势。修正公式如下：

Δωij(n)=αΔωij(n-1)+(1-α)ηΔf[ωij(n-1)]

(8)

式中：Δωij(n)为权值修正量，且已经加入了修改的记忆方向；η为学习速率；n为训练次数；α为动量因子，取值一般是0.1～0.8。

在BP算法中，提出了动量因子的改进后，可以有效改变网络训练的步长η，而不再是一个固定的值；同时，也可以改变修正权值的方向，即加入了一个扰动，有自动调节着步长的作用，可以向着平均的方向改变，从而不会产生太大的波动，并使误差变小。总之，引入动量项可以加快网络收敛速度，提高了预测的准确性。但是，其收敛速度相对还是太慢，预测效果存在一定的误差。所以本文提出了混沌量子粒子群算法，以提高算法预测风速的准确性。

2 CQPSO-BP算法

量子粒子群(quantum particle swarm optimization,QPSO)算法容易陷入早熟收敛，即当一个粒子发现一个最优位置时，其他的粒子就会迅速向它靠拢。如果这个位置只是局部最优点，则算法就陷入了局部最优，出现早熟收敛。在QPSO算法中，对粒子的位置采用量子位的概率幅进行编码，如式(9)所示：

(9)

式中：θ=2π×random,rondom为[0,1]之间的随机数；i=1,2,…,n，n为种群数量；j=1,2,…,B,B为空间的维数。

粒子的位置移动按式(10)更新：

Δθij(k+1)=ωΔθij(k)+η1r1(Δθ1)+η2r2(Δθf)

(10)

式中:ω为惯性权重；η1、η2为学习因子；r1、r2为随机数；Δθij为粒子在第j维的相位变化量；Δθ1为个体最优的相位变化量；Δθf为整个算法最优的相位变化量。

(11)

(12)

惯性权重ω的调整公式为：

(13)

式中:ωmax、ωmin分别为权值的最大值、最小值。

由于量子粒子群算法容易使粒子陷入早熟收敛，所以采用量子非门来加入变异操作，增加种群的遍历性:

(14)

本文针对QPSO算法的遍历性有限、容易陷入早熟收敛的特点，采用混沌的遍历性和随机性来弥补，即混沌量子粒子群优化(chaotic quantum particle swarm optimization,CQPSO)算法。该算法利用随机性产生B个参数(θ1,θ2,…,θB)，然后产生运动轨迹。每一个轨迹有n个序列，形成n×B个初始角。根据Logistic映射形成的混沌序列为：

x(k+1)=μx(k)[1-x(k)]

(15)

式中:x为混沌变量，x⊆(0,1)且x≠0.25、0.5、0.75;μ为控制参数。

3 CQPSO-BP算法的预测模型

3.1 数据集描述

由于输入变量和输出变量的量纲不统一，为了减小网络的误差，归一化的计算是必要的。它可以使数据之间的关系更容易体现，则预测的风速更准确。这里采用最大值最小值法，使所有变量限定在[0，1]之间。

为了验证CQPSO-BP算法预测能力的有效性，共选择3组不同维度的属于工业、教育和商业等行业的公开的数据集。运行在Windows10，8.00 GB内存，Inter(R) Core(TM) i7-8550U CPU @ 1.80 GHz环境下，基于Matlab R2019a中完成。

3.2 评价指标

为了评价本文建立的3种模型的预测性能，预测正确率至关重要。预测的准确率越高，误差越小，算法预测性能越好。本文选择准确率和3种评价指标来评价3种模型的预测性能，分别是准确率、MSE和MSPE。计算公式如下：

(16)

(17)

式中：N为测试样本个数；αi为第i个测试样本的实际值；βi为第i个测试样本的预测值。

3.3 CQPSO-BP算法流程

CQPSO-BP算法的主要流程如下。首先，输入样本数据，初始化种群的规模和变量数量，生成混沌初始化种群。其次，根据输入变量的个数，决定BP网络的结构，并初始化适应度值——即用 CQPSO-BP算法的粒子位置向量编码BP算法的权值和阈值中的相关参数，评价函数为网络的均方误差的倒数，以计算出网络的最优适应度值。再次，评价最优适应度值，判断有没有达到要求的精度或最大迭代次数。如果达到，则获得最优的权值、阈值。最后，判断网络误差是否满足预设要求，满足则输出预测值，不满足则算法继续迭代。同理，如果最优适度值没有达到要求，则算法继续迭代，直到达到预设要求为止。

CQPSO-BP算法流程如图1所示。

图1 CQPSO-BP算法流程图

3.4 仿真结果及分析

本文的数据来源于公开的、不同维度的数据集。在工业领域中，本文选择电力负荷的公开数据集，根据系统的运行特性、自然条件和社会影响等，预测未来某一时刻的负荷数据。该数据集维度是3。在教育领域中，选择从印度的角度预测研究生入学率的数据集，入学率就是被承认的机会，影响因素有GRE分数、托福成绩、大学评级、SOP、LOR、CGPA、研究成果，该数据集维度是7；在商业领域中，选择某商店中葡萄酒质量的样本数据集，影响的因素有颜色、温度、葡萄品种、土壤等，该数据集维度是11。三个数据集分别有1 200组、960组、1 020组数据，选择其中的200组、80组、60组数据作为测试样本。

在BP神经网络中，预测模型的每个神经元对应的作用函数为Sigmoid型函数，隐含层的作用函数为S型正切函数tansig，输出层的作用函数采用S型对数函数logsig。在网络中，训练的最大次数为1 000；训练要求的精度为1e-3；训练的学习速率为0.01。

本文中的输入变量根据维度选取，所以输入层设置为维度个数，根据Kolmogorov定理，网络中间层的神经元可取(2n+1)个，n为输入层神经元(维度)，输出变量有1个，所以输出层个数为1个。混沌量子粒子群算法的种群规模为20，最大迭代次数为60，惯性权重ωmax=0.9、ωmin=0.6,控制参数μ=0.36，学习因子c1=c2=2，变异概率为0.05。在Matlab平台上建立3种算法模型，然后分别仿真输出3种模型在电力负荷、研究生入学率、葡萄酒质量等级的预测结果对比。

电力负荷预测和实际电力负荷对比图、研究生入学率预测和实际入学率对比图、葡萄酒质量预测和实际葡萄酒质量对比图，分别如图2、图3、图4所示。

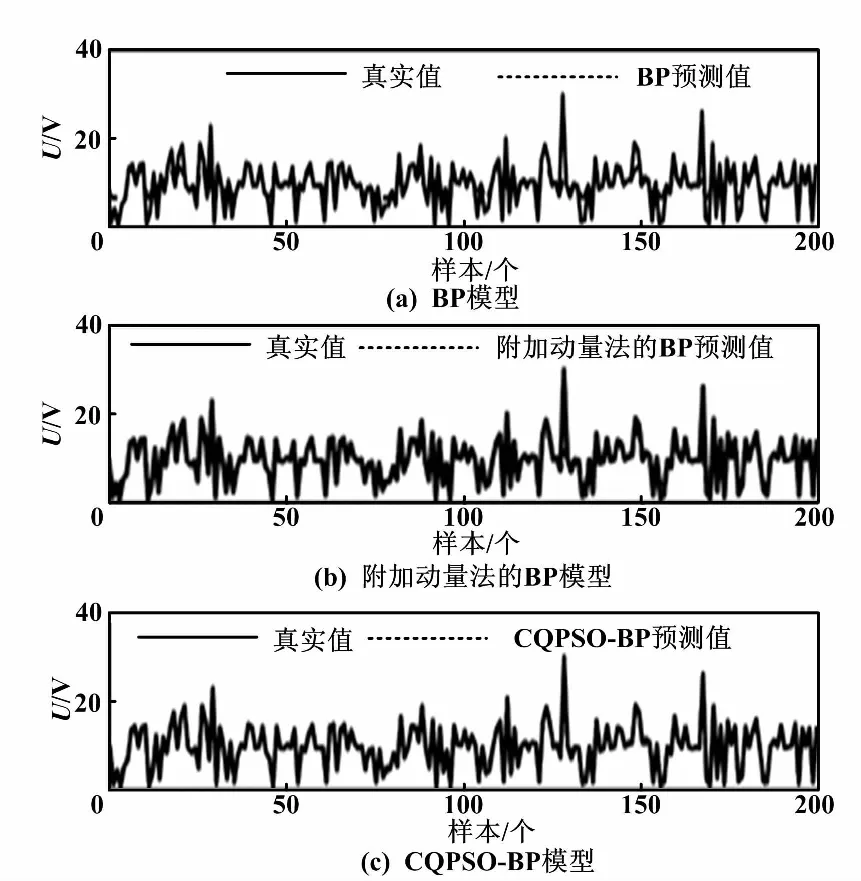
图2 电力负荷预测和实际电力负荷对比图

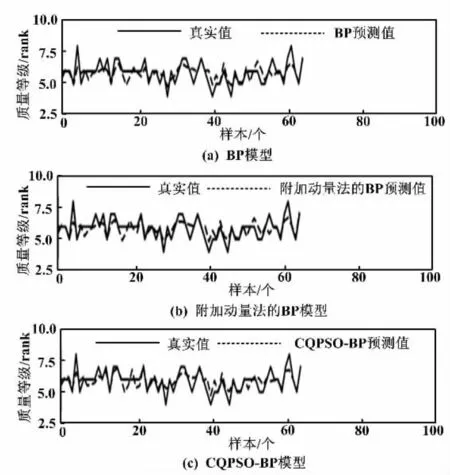
图3 研究生入学率预测和实际入学率对比图

Fig.3 Comparison of graduate enrollment rate prediction and actual enrollment rate

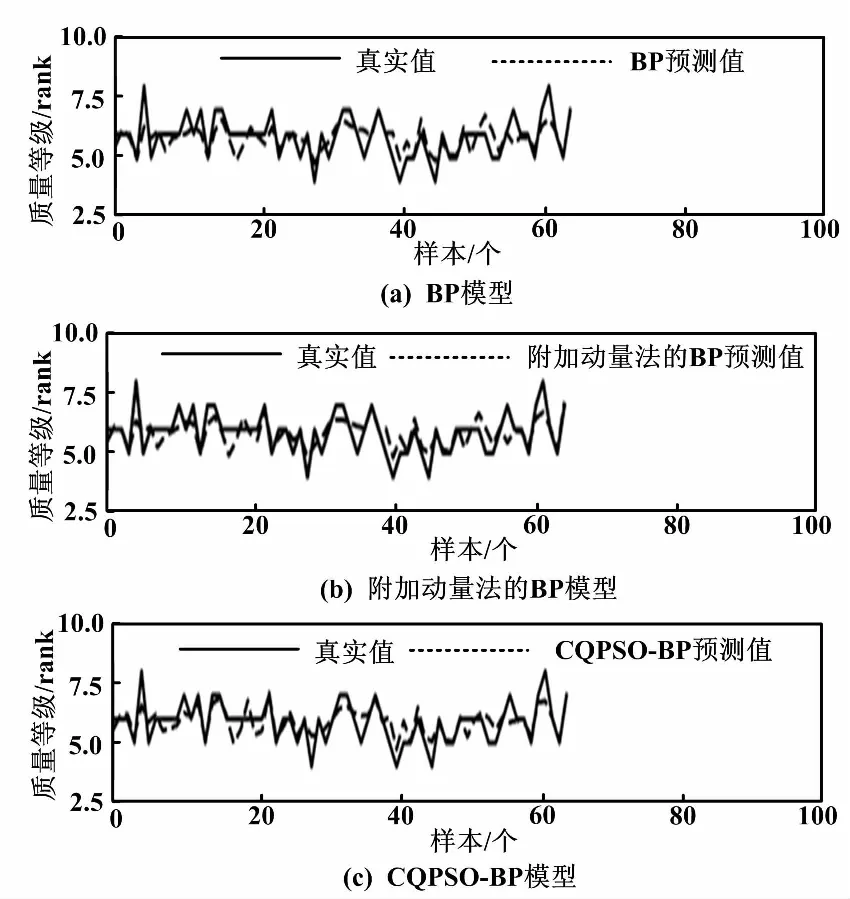
图4 葡萄酒质量预测和实际葡萄酒质量对比图

从图2～图4可以直观地看到，相比于传统的BP神经网络和改进的附加动量法，CQPSO-BP算法的预测效果有较明显的优势，而BP算法的预测效果是相对较差的。CQPSO-BP算法有较强的抗过拟合能力。3种模型在训练方法上都有所不同，预测的精度都不同。电力负荷预测的维度是3，研究生入学率预测的维度是7，葡萄酒质量预测的维度是11。在不同维度下，相同算法预测精度也不同。因为数据的不同，会影响预测效果。但CQPSO-BP算法的预测效果都是相对较好的，说明CQPSO-BP算法适用于预测模型。

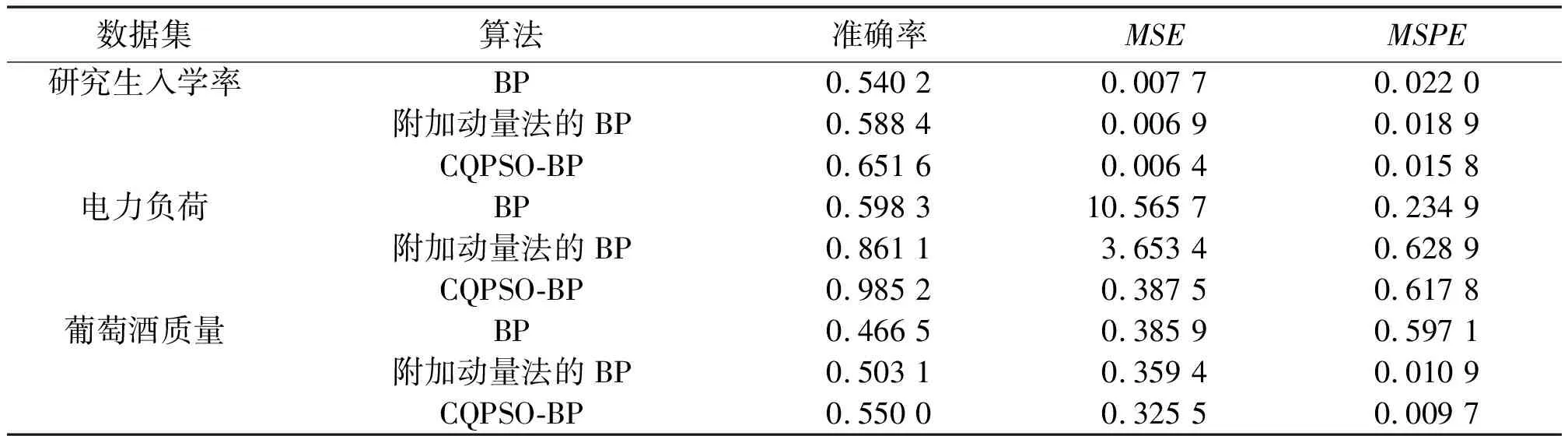
表1 3种算法的预测性能对比分析

表1中：准确率最大值为98.52%；MSE最小值为0.006 4；MSPE最小值为0.009 7。这3个评价指标的最优值都是在CQPSO-BP算法训练时取得。又因为电力负荷数据集的预测效果相对较好，预测值基本跟踪实际值，准确率最高。因此，选择这一组数据集来分析3种算法的的训练误差变化。误差曲线如图5所示。

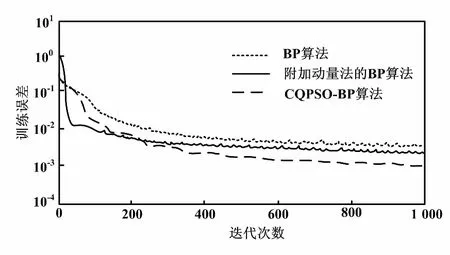
图5 3种算法的训练误差曲线图

从图5可以直观地看到，在电力负荷的预测模型中，当迭代次数最大值设为1 000时，BP算法的误差曲线图总体下降得较慢；在200步时开始更缓慢地下降；在1 000步时还没有收敛。通过附加动量法的BP算法改进后，该算法训练误差曲线图开始下降得较快，整体的训练误差比BP算法更接近预设要求。CQPSO-BP算法的训练误差相对下降得较快，在接近940步时达到收敛，完成训练，且此时误差达到预设要求为0.001。因此，CQPSO-BP算法的收敛速度最快，误差相对较小。

4 结束语

本文针对传统BP算法存在的过度拟合和预测精度不高的问题，提出了一种混沌量子粒子群BP算法。该算法将CQPSO算法与BP算法相结合，提高了种群的遍历性。用混沌序列初始化粒子的初始角位置，并引入变异操作，避免网络进入早熟收敛，从而对BP神经网络的权值和阈值进行优化。通过与附加动量法的BP算法和传统的BP算法进行对比，证明了CQPSO-BP算法的预测效果相对附加动量法和BP神经网络有明显的优势，也说明了CQPSO-BP算法有抗过拟合能力。在测试阶段，准确率、MSE、MSPE的最优值都是在CQPSO-BP算法训练时取得的。CQPSO-BP算法模型是适用于研究预测问题的一种模型，具有实际应用价值。