西部资源型城市经济增长与能源消耗关系计量研究

王 状，李效顺，张 琦，倪 衡，蒋冬梅

(1.中国矿业大学中国资源型城市转型发展与乡村振兴研究中心，江苏 徐州 221116；2.河南省城乡规划设计研究总院有限公司，河南 郑州 450044；3.南京农业大学中国土地问题研究中心，江苏 南京 210095)

改革开放四十年以来，中国以年均9.59%的GDP增长速度创造世界经济奇迹的同时却加速消耗着人类赖以生存的矿产资源，西部地区作为我国重要的能源基地，资源生产和消耗尤为显著。能源资源特别是煤炭资源起着支撑国民经济命脉的作用[1-3]，1985～1999年，全国和西部地区能源消费量总量分别以年均4.7%和4.5%的速度增长，进入21世纪以来更是以年均7%和8.3%的速度快速增长。

目前，国内外学者对能源与经济增长的贡献进行了系统研究，MUHAMMAD等[4]验证了十大能源消费国的经济增长与能源消费之间存在正相关关系。国内学者也在不同层面上用了多种方法探究能源与经济增长的关系，ZHANG等[1]认为中国大多数省份人均能源消耗与人均GDP存在关系；张智鹏[5]从全国层面上运用C-D生产函数对比分析了中国与部分OECD国家能源与经济发展依赖不同性；何则等[6]、张子荣[7]从全国层面上分别运用弹性脱钩指数和广义LMDI、VAR模型方法发现能源消费与经济增长具有强相关性；王迪等[8]、张晋娟[9]、李昭楠[10]从省级层面上分别揭示江苏省、山西省、甘肃省能源消费与经济增长之间的关系；栗继祖等[11]、孙喜民[12]认为资源型城市能源消费对中国经济增长起到重要作用，但同时也出现了很多问题。

以上文献大多从国家层面、省级层面研究能源与经济的关系，而针对问题更为突出、亟需转型的资源型城市的研究较少[11-12]。对此，本文拟建立改进的C-D生产函数模型分析经济与能源消耗的关系，定量测算西部典型煤炭资源型城市经济发展的主要因素，为城市转型发展的提供决策参考。

1 研究区概况

本文选取西部典型资源型城市鄂尔多斯市、阿克苏地区、榆林市、石嘴山市、庆阳市、攀枝花市、六盘水市和昭通市8市(地区)为研究对象，坐标范围为78°03′～111°27′E、25°19′～42°41′N，总面积为33万km2。截至2016年，常住人口数量为1 499.5万人，国内生产总值为12 289亿元。

研究区内蕴含着丰富的煤炭、石油、天然气、铁、钒等矿产资源。①煤炭城市：鄂尔多斯市位于内蒙古自治区西南部，已探明煤炭资源储量约占全国储量的1/6；榆林市位于陕西省最北部，54%的地下含煤，约占全国储量的1/5；六盘水市位于贵州省西部，有“西南煤海”之称，煤炭储量居全省首位；昭通市位于云南省东北部，煤储量居全省首位；石嘴山市位于宁夏回族自治区北部，是国家重要的煤炭工业城市。②油气城市：阿克苏地区位于新疆维吾尔自治区中部，石油、天然气储量丰富，“西气东输”工程气源的96.32%在阿克苏地区境内；庆阳市位于甘肃省最东部，是重要的原油生产基地。③金属城市：攀枝花市位于四川省南部，钛、钒储量位居世界第一和第三。

2 数据来源与研究方法

2.1 数据来源与处理

本文数据来源于云南省、贵州省、四川省、陕西省、甘肃省、宁夏回族自治区、新疆维吾尔族自治区和内蒙古自治区8省(区)1999～2017年统计年鉴、研究区8市(地区)统计年鉴，以及国民经济和社会发展公报等。

1) 实际GDP测算。为了去除价格因素对结果的影响，将现价GDP转为实际GDP，本文拟以1985年为基年计算实际GDP，计算公式见式(1)。

Rt=Rt-1×It

(1)

式中：Rt为第t年的实际GDP；Rt-1为上一年的实际GDP；It为当年的GDP指数。

2) 资本存量测算。由于Solow改进的C-D生产函数中的资本是资本存量，所以需要将每年的固定资产投资额转换为资本存量。目前，常用的资本存量测算方法是永续存盘法[13]，计算公式见式(2)。

Ct=Ct-1×(1-ρt)+It

(2)

式中：Ct为第t年资本存量；Ct-1为上一年的资本存量；ρt为第t年的经济折旧；It为第t年的固定资产投资额。

本文以1985年为基年，利用已有文献得到1985年各省的资本存量[14]，并按本年固定资产投资比例估算出研究区城市资本存量，经济折旧率定为9.6%[15]，以此来测算每年的资本存量。

2.2 研究方法

1) 模型基础。传统经济理论认为经济增长主要依靠劳动和资本，美国数学家COBB Charles和经济学家DOUGLAS Paul构建出以劳动和资本为核心，推动经济增长的C-D生产函数，表达式为Y=CKaLb。其中，参数Y为产出、K为资本投入、L为劳动投入、C为技术水平；a、b分别为资本与劳动的产出弹性。传统经济理论虽然引入了技术要素C，但是仅将它作为独立于其他要素之外的一个不变的参数。显然，现实情况中技术要素并非固定不变，技术水平在不断提高。因此，SOLOW于1957年提出了改进的C-D生产函数模型：Y=A(t)KaLb，该模型加入时间指数趋势，以测定技术进步，参数A(t)为技术的年进步速度；t为年份序列。Solow改进的C-D生产函数模型弥补了技术进步测定的遗憾，能够更好地描述资本、劳动投入和技术进步对经济增长的贡献[16-17]。

2) 模型改进与构建。Solow改进的C-D生产函数加入了技术要素对经济发展的作用，但仍围绕劳动和资本两要素，未考虑能源消费和采矿用地要素对经济发展的影响。结合实际研究发现，经济发展并非仅仅是劳动和资本两要素作用的结果，与能源也有较强的相关性。因此，本文在改进的C-D生产函数基础上，借鉴相关学者的研究成果[18-20]，实证分析与定量测算各投入要素对中国经济增长的具体贡献，并把握其内在作用机制。由于资源型城市经济发展中第一产业(即广义的农业)GDP增加值的贡献度较小，故本文确定的因变量为第二产业、第三产业GDP(国内生产总值)增加值，确定函数自变量分别为劳动力、资本、能源。基于以上考虑，重新构建改进后的C-D生产函数见式(3)。

GDP=C×(1+f)t×(SI)a×(WF)b×(EC)c

(3)

式中：f为年技术增长率；SI为资本贡献率；WF为劳动贡献率；EC为能源消费贡献率；C为经济技术常量；t为年份；a、b、c分别为各因素的产出弹性系数。

为了消除异方差和便于参数估计，对式(3)取对数，具体的函数形式见式(4)。

lnGDP=lnC+tln(1+f)+aln(SI)+

bln(WF)+cln(EC)

(4)

根据C-D生产函数的性质，当a+b+c>1时，表示规模报酬递增，加大要素投入能带来更大的产出量，即规模经济，此时应加大要素的投入；当a+b+c<1时，表示规模报酬递减，追加投入只能带来较小比例的增加，即规模不经济，此时应停止追加要素的投入；当a+b+c=1时，表示规模报酬不变，产出随投入量同比例增加。

3 结果分析

3.1 经济发展现状分析

本文选用经济增长率与能源消耗增长率两个指标，分析经济发展与能源消耗之间的内在联系，二者趋势图如图1所示。

1999～2016年间，研究区经济一直维持着高速增长，经济增长率在2005年左右出现拐点，呈现先上升后下降的趋势。与此同时，研究区能源消耗也呈现先上升后下降的趋势，但其在2008年出现拐点，滞后于经济增长率拐点出现时间。总体而言，经济增长和能源消耗虽然波动幅度较大，出现拐点时间不一致，但变化趋势较为吻合。

通过以上分析表明，能源消耗波动趋势与经济增长整体变动态势基本一致，经济增长与能源消耗之间必然存在一定联系，构建相应模型对其关联性进行分析具有可行性。

3.2 参数估计结果

本文以六盘水市数据为例对参数估计过程进行分析，其他7市(地区)进行相同的处理和估计即可。

1) 单位根检验。首先对六盘水市1998～2016年数据进行单位根检验，检验结果见表1。

由表1可知，两种检验方法原假设均为“序列为I(1)即一阶平稳”，结果表明“level”下均不平稳，一阶差分后均表现为平稳状态，符合协整检验条件。其他7市(地区)按同样方法进行数据处理，发现昭通市能源消费量和从业人员两项数据未能通过一次差分后的单位根检验，故将其舍弃。

2) 协整检验。在单位根检验之后，发现六盘水市1998～2016年数据符合协整检验条件，因此进行协整检验，检验结果见表2。

图1 研究区经济增长率与能源消耗增长率关系Fig.1 Comparison of economic growth rate and the growth rate of energy consumption(资料来源：中国经济与社会发展统计数据库；研究区各市(地区)统计年鉴)

表1 1985～2016年六盘水市数据单位根检验结果Table 1 Unit root test on variable of Liupanshui city from 1985 to 2016

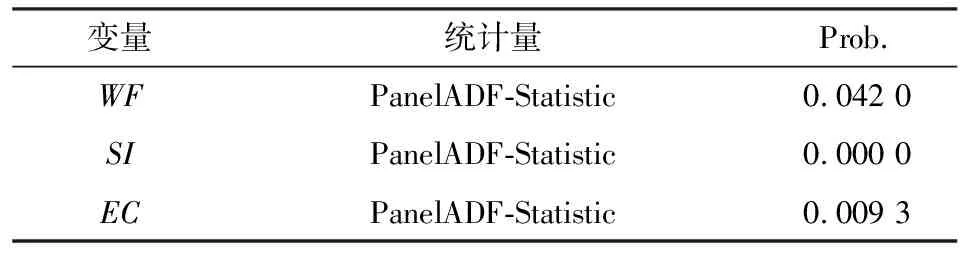
表2 协整分析结果Table 2 Results of panel cointegration test

上述检验的原假设都是“不存在协整关系”，表2结果表明，六盘水市四个自变量与因变量之间存在着长期均衡关系，因此，有必要对模型进行参数估计。其他6市(地区)按同样方法进行数据处理。

3) 参数估计。在Eview6.0软件平台上，采用最小二乘法对六盘水市1998～2016年数据进行回归模拟，发现ln(C)显著程度偏低，故将其剔除，认为(C=1)。求得函数表达式见式5。

ln(GDP)=tln(1+0.135)+0.20ln(SI)+

0.42ln(WF)+0.23ln(EC)

(5)

其回归结果显示：R2为0.999 4，F统计量为4 445.9，D-W值为1.8，T检验值通过显著性检验，说明建模整体上对样本拟合很好，回归方程显著，结果可信。确定最终模型见式6。

GDP=

(1+0.151)t×(SI)0.20×(WF)0.42×(EC)0.23

(6)

利用该思路方法对研究区7市(地区)进行参数估计，得到模型参数估计结果见表3。

表3 研究区7市(地区)模型参数估计结果Table 3 Estimation results of model parameters of7 cities (regions) in the study area

注：*为自变量T和F检验值未通过10%显著性检验

对其他6市(地区)进行同样处理和参数估计发现，R2均大于0.98，拟合度较高，自变量T和F检验值大都通过10%显著性检验。

3.3 参数估计结果分析

1) 驱动因子分析。对影响经济发展各因素的弹性系数进行分析，将最大的弹性系数因素定义为地区经济发展的主要驱动因素。按照此分类方法，可将城市发展分为：能源驱动型城市、投资驱动型城市、劳动驱动型城市、劳动与投资双核驱动型城市四种类型。其中，能源驱动型城市有攀枝花市、石嘴山市、庆阳市；投资驱动型城市是阿克苏地区；劳动驱动型城市有鄂尔多斯市、六盘水市；劳动与投资双核驱动型城市是榆林市。同时结合各地区自然本底条件和资源禀赋状况可以得出，煤炭城市中鄂尔多斯市、六盘水市为劳动力驱动，榆林市为劳动与投资双核驱动，石嘴山市为能源驱动；油气城市中阿克苏地区为投资驱动，庆阳市为能源驱动；金属资源城市攀枝花市为能源驱动。

2) 规模报酬阶段分析。分析系数和可知，六盘水市、榆林市、攀枝花市、鄂尔多斯市、石嘴山市、庆阳市系数和小于1，处于规模报酬递减阶段，只有阿克苏地区系数和大于1，处于递增阶段。相对而言，系数和高的城市应该投入更多要素支撑其进一步发展。

3) 科技水平进步率分析。综合科技进步率反映科技进水平对地区经济发展的贡献度，通过分析表3数据，可得7市(地区)综合科技进步率差异显著，由大到小排序为：石嘴山市(7.96%)>庆阳市(5.39%)>攀枝花市(3.55%)>榆林市(3.24%)>鄂尔多斯市(2.64%)>六盘水市(1.35%)>阿克苏地区(1.24%)，数值大的地区说明技术进步对经济增长的影响作用较强。

4 结 论

1) 西部城市经济增长与能源消耗存在正相关关系，1999～2016年研究区经济增长率与能源消耗率均呈先上升后下降的趋势。

2) 西部城市经济增长的驱动因素不同。首先，西部城市经济增长与城市资源类型息息相关。研究区内煤炭城市主要是劳动力带动，这主要是因为煤炭产业是劳动密集型产业，但仅依靠投入廉价劳动力，不能达到规模报酬递增，还需要引进新的科学技术替代原有的“人海”模式。新疆阿克苏地区处于规模报酬递增阶段，应持续投入资金和劳动力促进当地经济发展，加强当地人才培养，实现“引人、育人、用人”的良性循环。其次，西部城市经济增长对能源消耗的依赖性强，能源消费并不能使经济达到规模效应，需要及时转变传统能源消费结构。

综合判断，西部许多城市只依靠资源将难以可持续发展，应结合当地自然本底条件和矿产资源特性，选择合适领域进行产业转型，引进高素质人才，提高劳动力素质，培养科技创新能力，探索适合自身发展的新策略和新模式，为实现地区长远发展提供保证和支持。