大角度受控离心力对系统的无工质推进方法研究

孙璐 孙长利 张拥军 刘辉

摘   要：对大角度受控离心力的无工质推进方法做了基础的力学理论探讨。通过利用向心力与离心力的作用与反作用性质，对单一系统使用其内力实现无工质推进方法的可行性进行解析。此研究可用于航天器、导弹和水利工程水下探测等的无工质推进动力技术领域。

关键词：镜像对称  大角度  受控离心力  惯性系  无工质

中图分类号：O313                                  文献标识码：A                        文章编号：1674-098X（2019）08（a）-0049-04

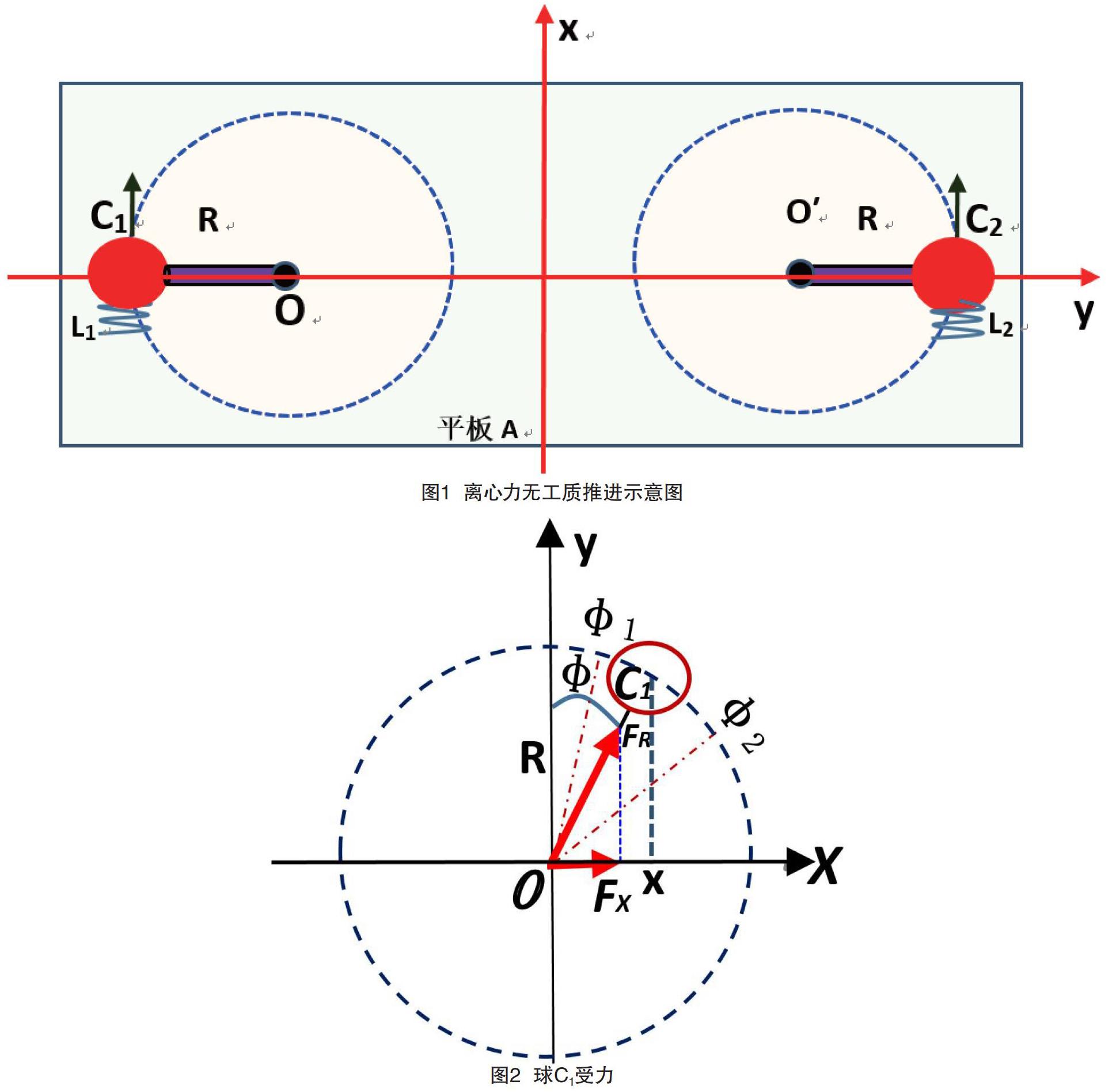
已对小于临界角（以下简称小角度）的内力对系统的无工质推进技术进行了研究[1-2]。小角度无工质推进，其有效推进动力源于较小区间，动力作用的位移小，推进动力输出不足。因此有必要对大于临界角（以下简称大角度）的无工质推进做探讨，通过延长系统内部动力持续作用的位移，根据数值计算和设计，对大角度和小角度的推进方法做以比较，做到取长补短，优势互补，以达到增强推进动力输出效能的目的。说明：（1）此课题是建立在转动物体的向心力与离心力遵循作用力与反作用力基础上的，即离心力是向心力的反作用力，二者等值反向[3-4]。（2）参考图1，采用镜像对称设置的偏心装置，其离心力的无工质推进，是通过对离心力的有效控制，使离心力始终在一个方向（y轴）的合力为0，这个力对系统的平动和转动无影响，即可不考虑这个力的问题。只允许离心力在另一个方向（x轴）的分量起作用，即只关注此力的作用。（3）系统无外力，由动量守恒和机械能守恒，理论讨论始终把握两个方面的问题：其一，转动物体（球）C的向心力在x轴方向的分量对C所产生的冲量，其数值大小既等于转动物体C动量的改变量，也等于向心力的反作用力——离心力在x轴方向分量对全系统A所产生的冲量，还等于离心力在x轴方向的分量对系统A所产生的动量的改变量[5]。其二，向心力在x轴方向的分量对转动物体（球）C所做的功，其数值大小既等于转动物体C动能的改变量[5]，（4）也等于向心力的反作用力——離心力在x轴方向的分量对全系统A所做的功，还等于离心力在x轴方向的分量对全系统A所产生的动能的改变量。由向心力与离心力等值反向，为方便计算，算法中常做互相替代使用。

1  圆周运动的向心力与离心力是作用力与反作用力

结合图2，向心力只产生于转动物体，不转动的物体没有向心力;向心力作用的效果是使本应作直线（沿切线方向）运动的物体，因受到垂直其运动方向力的作用，才改作圆周运动的;转动物体通过转动轴对整个系统施以离心力作用，离心力作用于承装转动的整个物体系统。向心力和离心力所在的同一直线不变，但随着转动物体位置的变动而改变，且符合牛顿第三定律[1-4]。

设想：对系统采用镜像对称的偏心结构设置，偏心物体部分做镜像转动，使y轴方向的合力为0，即系统在y轴方向上始终处于平衡状态，只利用其在x轴上分力的作用。使用弹力、电磁力等沿偏心装置（球）m圆周运动切向上的作用力，使m做加（减）速转动，对整个系统沿x轴方向上合成的宏观平动贡献为0，即切向力不影响系统的平动。该切向作用力在前半周（0→π）使m做高速转动，向心力数值大，即向心力在x轴方向分量的平均值大;后半周（π→2π）使m做低速转动，向心力数值小，即向心力在x轴方向分量的平均值小。由于前、后半周的向心力在x轴方向的分量做功所经过的位移相等，即转动的偏心装置（球）在前、后半周的向心力沿x轴方向的分量所做功的数值不等，且向心力与离心力等值反向，系统无外力，即机械能守恒，若存在向心力在x轴方向的分量对偏心装置（球）m做的功（以及所具有的能）完全转化为其反作用力——离心力在x轴方向的分量对系统A做的功（以及所具有的动能），可使系统A在前半周获得向前的做功数值大于其在后半周向后的做功数值，则系统在x轴正方向上可产生宏观的平动效果，且前、后半周做功差值越大，系统在x轴正方向上所获得的平动效果越强。这就是受控离心力对系统的无工质推进方法的设想。为便于直观，以下讨论以弹簧力为例。

2  系统内部离心力推进作用的解析

2.1 弹簧力冲击偏心装置（球）的质心，所构建的模型，其工作过程分两步

如图1，光滑水平面，初始静止的平板装置系统A，镜像对称装有2个质量均为m的球C1、C2（球质心位其打击中心），分别绕垂直纸面的轴O、O′转动。球与平板A间分别有被压缩弹簧L1、L2，转动半径同为R（亦为回转半径），平板装置A全系统的质量为M。鉴于球C1、C2采用镜像对称设置，为便于研究，分析以球C1为例。（球C2类同，讨论略。相对观察者建立平面直角坐标系，系统不计摩擦）。系统工作过程分两步：

第1步：如图1，弹簧L1和L2同步释放，在0→π区间内，两弹簧分别给予球C1、C2沿其圆周运动切向的弹力作用，C1、C2作镜像的加速转动;整个平板A系统在C1、C2转动向心力的反作用力——离心力作用下，沿x轴正方向运动。

此弹簧释放过程中，对于球C1、C2沿其圆周运动切向上的弹力作用，尽管存在平板A与球C1、C2间的反冲运动，基于平板A与两球共为同一系统，根据质心运动守恒定律，此作用在沿x轴方向上的平动合成效果为0，即切向力不影响全系统宏观的平动。

第2步：在π→2π区间内，两弹簧分别给予球C1、C2沿其圆周运动切向相反方向的弹力作用，C1、C2作镜像的减速转动;整个平板A系统在C1、C2转动向心力的反作用力——离心力作用下，沿x轴的反方向上运动（或趋势）。

由于球C1、C2在0→π内处于高速转动区间，其离心力在x轴正方向上分量的平均值大;球C1、C2在π→2π内处于低速转动区间，其离心力在x轴负方向上分量的平均值小于在0→π区间的平均值。则球C1、C2在0→2π的周期（T）内，两者的离心力在x轴方向上的分量对整个平板A系统，合成产生沿x轴正方向的宏观平动效果。如用电磁力代替弹簧力，并在1T、2T、3T、4T……等周期重复作用，这是利用离心力沿x轴方向上的分量，在两个半圆周上做功的差值（简称功差），实现对系统的自主推进，属于电推进类型[6]。

2.2 反冲运动的回顾

球C1、C2与力臂（半径）R脱离，弹簧L1、L2同步释放，两球与平板A之间发生反冲运动，动量守恒。以球C1为例，即

弹簧释放完成后，两球做直线背离运动，所获得能量与其质量成反比[1]，即系统的小质量物体（m）所获得弹簧能量的份额大，大质量的物体（M）所获得弹簧能量的份额小，弹簧能量的大部分转移到小质量的物体上。

2.3 切向力的作用

2.3.1 偏心装置（球C1）受到沿圆周切向力的作用，角动量守恒

如图1，弹簧释放（时间t1→t2），球C1受到弹簧力作用产生绕轴O的顺时针加速转动，弹簧的能量大部分转移给小质量的物体C1上（见上文2.2），（系统始于靜止，即平板系统的初速，末速vM;球C1初速v0=0，末速v），切向力及其反作用力的作用：

球C1切向力的反作用力产生的冲量矩，使平板A产生逆向转动。基于球C2与C1是镜像对称设置，C2与C1的转动，其切向力的反作用力所产生的冲量矩，使整个平板装置A共同转动的作用效果互相抵消，整个平板A不转动。切向力产生的冲量矩只使球C2与C1转动。

2.3.2 球C1在0→π内受切向力在x轴方向上分量的作用与其反作用力对系统A的作用

球C1在0→π内受到切向力在x轴方向上分量的作用与其反作用力对系统A的作用，符合任一时刻（如C1转动至φ角，切向速度v，相对应系统A的沿x轴平动速度vM）沿x轴方向上的平动量守恒。即：

C2在0→π内受切向力及其反作用力的作用，任一时刻沿x轴方向上的平动量守恒[5]。

结果：弹簧对球C1的切向力，其力矩的作用使球 在0→π区间内做加速转动，但由于球C2（偏心装置）与C1是镜像对称设置，二者其切向力的反作用力的冲量矩共同作用使平板A的转动效果互相抵消，即整个平板装置A不发生转动。切向力与其反作用力的作用使球C2、C1与平板装置A二者在x轴方向上平动量守恒，符合质心运动守恒定律，即切向力与其反作用力产生平动量的合成效果对整个平板装置A系统的平动无影响。总之，弹簧释放，其切向力及其反作用力的作用，只使球（偏心装置）C1、C2做圆周运动，对整个平板A系统的平动效果无影响[5]。

2.4 离心力的推进作用

2.4.1 球C1在0→π区间内转动离心力的作用

3  算例

如起始静止球C1在0→π区间内的0→段被弹力冲击加速至v，接下来转入匀速圆周运动至π;球C1在π→2π区间内的π+∣φ'∣段被弹力冲击减速为0.5v，接下来转入匀速圆周运动至2π。该周期离心力在x轴方向的分量对平板A系统有效推进效果，如表1。

4  结语

镜像对称设置的系统A，其球C1在0→2π区间的转动，前半周的初速度和末速度，分别是其后半周的末速度和初速度，即球C1在0→2π区间转动的沿x轴方向上的平动量是守恒的;但球C1在0→2π区间转动的离心力沿x轴方向上的分量在前、后半周所做的功不等，前半周做的功大于后半周做的功，即在两个半圆周上所做功的差值（简称功差）不为0，又球C2与之类同，从而实现离心力对系统沿x轴正方向的无工质自主推进;就提高其推进输出效能，可根据具体实际需要，采用本文的算法，结合计算数值、设计和实验，充分发挥大角度离心力推进动力的优势，以选取优化方案。它与火箭、枪炮等利用反冲运动是两类不同的推进方法，为与参考文献[1]、[2]的推进方法区分开，称之为大角度受控离心力对系统的无工质推进方法。

文中离心力推进动力的能量是由弹簧提供的，但其基础的力学理论，尤其对大角度离心力推进，同样适用于以电动机引擎取代弹簧力工作的变换。采用电动机（平板A做为机座）驱动，其推进动力分别通过轴O、O'、经力臂R传递给偏心装置C1、C2，电动机产生的使偏心装置转动的切向力及其冲量矩，与电机定子部分（含机座装置A）受到的反作用力及反向冲量矩之间分别遵循动量守恒、角动量守恒，有必要对大角度电磁驱动无工质推进问题作进一步研究。

参考文献

[1] 孙璐.内力用于系统的无工质自主推进方法研究[A]//中国电工技术学会电磁发射技术专业委员会.全国第八届电磁发射技术研讨会论文集[C].2017.

[2] 孙璐.电磁驱动式无工质牵引器：中国，201721222213.4[P].2017-09-22.

[3] 许国基.浅谈离心力物理教学[J].南宁，1989（5）：33-34.

[4] 周树荣.对作圆周运动的物体存在离心力的论证[J].教育界，2010（7）：57-58.

[5] 任才贵.小球与均质自由杆的碰撞大学物理[M].北京：高等教育出版社，2006.

[6] 张敏，杭观荣.电推进──空间技术革命[J].中国航天，2016（2）：7-12.

[7] 汪诚义.考研数学：高等数学与微积分[M].北京：中国物资出版社，2008.

[8] F.W.SEARS等著，恽瑛等译.大学物理学[M].北京：高等教育出版社，1983.

[9] 关治，陈景良.数值计算方法[M].北京：清华大学出版社，1998.