密集颗粒流动的连续性方法应用研究

孙 倩，彭天骥，严 安，周志伟,*

(1.清华大学 核能与新能源技术研究院，北京 100084；2.中国科学院 近代物理研究所，甘肃 兰州 730000)

颗粒物质存在于生产和生活的众多方面。在食品、化工等工业领域，原材料通常以颗粒形式存储于筒仓中。我国重点发展的球床模块式高温气冷堆(简称高温气冷堆)，几十万球形燃料颗粒紧密堆积，在重力驱动下流动。中国科学院近代物理研究所创造性地提出了新型流态固体(mm级钨)颗粒靶概念[1]。然而到目前为止，人们对颗粒流机理认识不深，没有完善的本构模型能描述颗粒的流动[2-3]。

为描述颗粒的流动，根据研究目的和精度需求，提出了很多方法[4-6]，整体上可分为两类：离散单元法(DEM)和连续介质力学方法。离散单元法[6]是把整个介质看作由一系列离散的独立运动的单元所组成，单元本身具有一定的几何和物理特征。其运动受经典运动方程控制，整个介质演化由各单元的运动和相互接触来描述。连续介质模型则忽略颗粒系统的离散性和单个颗粒的特性，利用连续性的假设，用统一的计算模型代替所有离散的颗粒。从物理角度，离散单元法更符合离散体系本身的特性。但从工程角度，将颗粒介质进行连续化处理，发展适合颗粒介质大变形的数值方法，一方面能减少计算量，另一方面能复现颗粒集合的运动现象，更好地为灾害防治和工业应用提供参考[7]。

本文基于物质点方法，采用μ(I)流变模型，实现用连续性方法模拟密集颗粒流动的计算框架，用于颗粒堆积坍塌和重力驱动下颗粒在漏斗流动过程中的模拟，并与物理实验和DEM计算结果进行对比。

1 连续体本构方程

根据流动特点，颗粒流通常可分为准静态流、快速流和慢速流3种流态，分别对应类固、类气、类液状态。当颗粒处于准静态流状态时，可用弹塑性理论对其进行描述；对于处于快速流动状态的颗粒物质，人们发展了颗粒动理论来描述该流态下颗粒物质的本构关系[8]。而对于介于快速流与准静态流之间的过渡状态，颗粒像流体一样流动，相互间又保持着相对持续的接触，塑性理论和颗粒动理论都不适用。Midi[9]和Jop等[10]受黏塑性和宾汉塑性流体行为的启发，根据大量的数值和物理实验，提出了描述密集颗粒流动的本构方程，即局部流变模型，较好地复现了颗粒在不同边界下的流动。该模型在宏观尺度上对颗粒介质的耗散描述是通过有效摩擦系数μ=τ/p(τ为剪切应力，p为正应力)实现的。

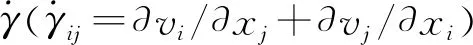
τ=μ(I)p

(1)

式中，μ(I)为颗粒物质体系的总摩擦系数，是复杂力链响应的宏观体现，与惯性系数I有关。

(2)

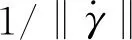
μ(I)流变模型认为式(1)中的摩擦系数μ(μ=τ/p，图1)可表示为：

(3)

式中：μs为颗粒介质在零剪切率下的最小摩擦系数；μ2为高速流态下摩擦系数的上限；I0为常数。

图1 摩擦系数μ(I)与惯性系数I的关系[10]Fig.1 Friction coefficient μ(I) as a function of inertial number I[10]

结合针对颗粒固态的弹塑性理论和适用于颗粒液态的μ(I)黏塑性模型，即可描述颗粒的固态行为和液态行为[11]。定义颗粒介质的柯西应力张量为σ，应力偏张量σ0=σ-(trσ)I/3，颗粒介质的运动速度为v。则速度梯度张量L=gradv，L可分解为旋率张量W=(L-LT)/2和变形率张量D=(L+LT)/2。D可认为由其弹性部分De和塑性部分Dp组成，即D=De+Dp。

颗粒介质的质量守恒方程可表示为：

(4)

动量守恒方程可表示为：

(5)

式中：b为颗粒介质所受到的体积力；ρ为颗粒介质的密度。

焦曼应力率为：

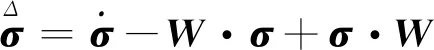
(6)

当颗粒处于弹性稳定态时，体系内无塑性应变。本构关系用弹性变形率表示为：

(7)

其中：E为杨氏模量；υ为泊松比。定义颗粒介质的剪切力τ、压力p和摩擦系数μ如下：

τ=‖σ0‖，p=-(trσ)/3，μ=τ/p

当颗粒介质的摩擦系数μ大于其屈服摩擦系数μs时，发生弹性失稳，引发塑性流动，这时μ(I)流变模型被用作黏塑性流动法则。即：

(8)

2 物质点计算方法

Sulsky等[12]将用于流体动力学的质点网格法(PIC)扩展到固体力学问题中提出了物质点法(MPM)。MPM采用携带材料所有信息的物质点离散材料区域，以表征材料区域的运动和变形状态，并避免了处理对流项；采用规则的欧拉背景网格计算空间导数和动量方程，从而实现了质点间的相互作用与联系，并避免了网格畸变问题，非常适合处理涉及材料特大变形的问题[13-14]。

以颗粒介质为例，物质点法将材料区域离散为1组相对背景网格运动的质点，如图2所示。每个质点表示1个材料团簇，并携带其所有物质信息，如质量、速度、应力和应变等。背景网格仅用于求解动量方程和物理量的空间导数，一般取为固定于空间的规则网格。

图2 物质点方法[13]Fig.2 Material point method[13]

将连续体离散为质点后，其密度近似为：

(9)

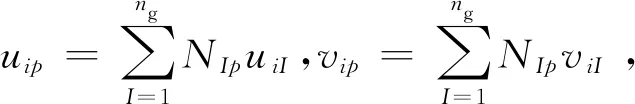
物质点法将连续体离散为一系列质点，质点携带的质量在运动过程中保持不变，故质量守恒方程(4)自动满足，因此主要求解动量方程。动量方程(5)的求解是基于其更新拉格朗日式的控制方程的弱形式[13]。

(10)

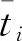
本文基于物质点方法，根据μ(I)理论模型添加本构关系式(7)、(8)，对密集颗粒的流动进行模拟。本文的整体计算流程如图3所示。

3 颗粒介质坍塌模拟

颗粒坍塌是颗粒流动的一个典型现象[15]。清华大学孙其诚曾针对颗粒坍塌过程做过物理实验[16]。实验装置如图4所示，实验区域是1个60 cm×20 cm×20 cm的箱子，颗粒的初始堆积体积为10 cm×18 cm×20 cm。实验中使用了约24 000颗粒径5 mm的陶土颗粒，颗粒的杨氏模量E为5.5 GPa，泊松比为0.3，颗粒介质的表观密度为2 200 kg/m3，陶粒堆积形成锥角的平均值为22°。

图3 MPM计算流程Fig.3 Calculation procedure of MPM

采用MPM模拟图4的实验，材料参数取μs=tan(22°)=0.404，μ2=0.64，I0=0.28[9-11]。模拟中共采用11 520个物质点。在x=0和x=60 mm处设置对称边界，约束x方向动量；底部为固定边界，侧壁采用对称边界。颗粒初始堆积的离散间距为2.5 mm，网格边长为5 mm。DEM模拟采用开源软件LIGGGHTS，选用Hertz-Mindlin接触模型。参照文献[15]的做法，在底部铺设1层固定的微小颗粒来模拟实验中的底部粗糙砂纸。

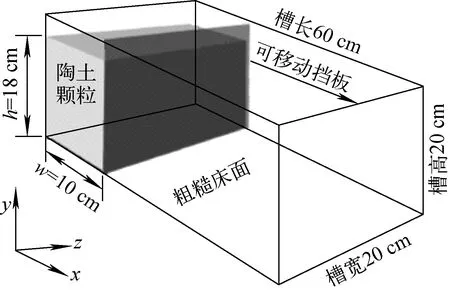
图4 颗粒坍塌实验装置示意图[3,16]Fig.4 Experimental setup of granular collapse[3,16]

图5示出了实验、MPM模拟和DEM模拟坍塌过程中的颗粒介质速率分布情况。可看到，从0 s撤掉挡板后，颗粒体在重力作用下加速崩塌；到0.16 s时，颗粒速度达到最大值；到0.32 s时，重力的加速作用逐渐减弱，由于壁面和内部的摩擦力，颗粒开始逐渐减速；到t=0.72 s时，大部分颗粒均已重新恢复静止状态。

图5 颗粒坍塌实验和MPM及DEM数值模拟结果对比Fig.5 Results of experiment, MPM and DEM for granular collapse

从图5可明显看出，MPM模拟速率分布和实测速率分布以及DEM模拟结果基本相同。

4 漏斗流动

4.1 卸料速度

漏斗的一个重要参数是卸料速度。该参数影响颗粒材料在工业中的运行状态。因此，能否预测漏斗的卸料速度是判断一个模型能否具有预测漏斗流动的重要标准。Beverloo根据大量的实验数据，得到了矩形漏斗的卸料速度经验关系式[8]：

(11)

本文模拟的矩形漏斗尺寸如图6所示，H=1 m，L=1 m。考虑到纵向深度W≫D，故纵向上采用周期性边界条件。漏斗沿中轴面对称(图中虚线所示)，模拟时只模拟一半几何，中轴面处采用对称边界，侧面壁面采用无摩擦边界，底部壁面采用完全摩擦边界。模拟时网格尺寸为0.01 m，材料参数与坍塌算例的一致。

图6 矩形漏斗示意图Fig.6 Schematic diagram of silo

图7为D=0.14 m、H=1 m时漏斗卸料的瞬态速度分布。在漏斗出口正上方，颗粒快速流动；靠近壁面区域，颗粒稠密堆积，几乎不流动；漏斗中心轴附近的颗粒紧密堆积，缓慢流动。

图8为不同填充高度和出口尺寸下漏斗的剩余质量变化。从图8a可看出，当漏斗出口宽度D=0.14 m时，不同高度下，漏斗的剩余质量均随时间线性减少，说明卸料过程是以稳定的质量流量进行的。不同初始填充高度下，直线的斜率相同，说明初始填充高度对卸料速率没有影响，这与经验结果一致。从图8b可看出，不同出口尺寸下，漏斗均以稳定的质量流量卸料，出口尺寸越大，斜率越大。

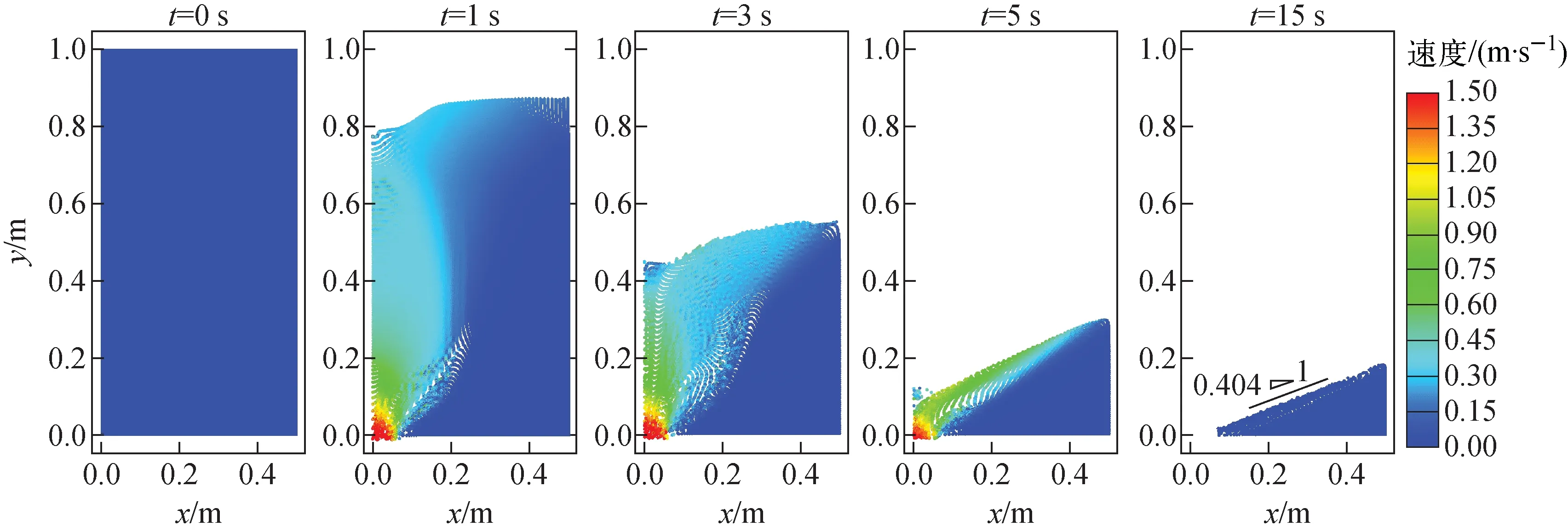
图7 t=0、1、3、5、15 s时漏斗卸料的速度分布Fig.7 Velocity throughout discharge process at t=0, 1, 3, 5 and 15 s

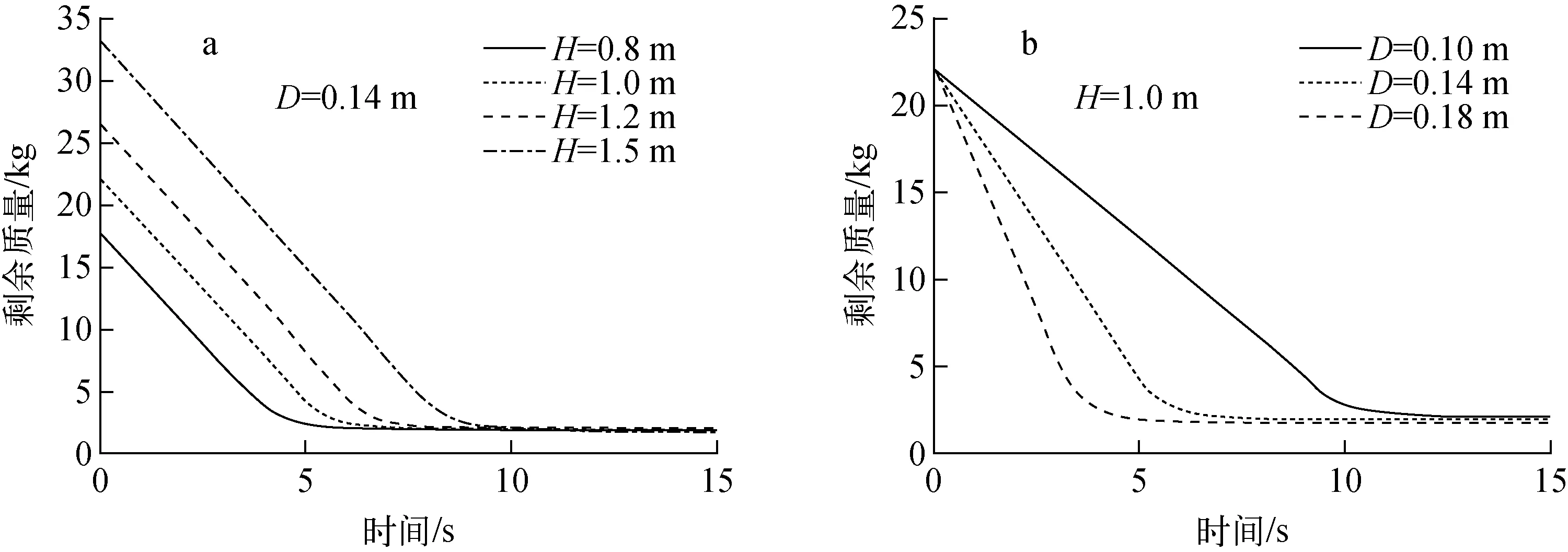
图8 不同填充高度和出口尺寸下漏斗剩余质量变化Fig.8 Mass remaining in silo for different initial mass and different hole sizes

图9 卸料率与出口尺寸D的关系Fig.9 Variation of discharge rate versus outlet size

4.2 ADS颗粒流靶

在加速器驱动次临界系统(ADS)中，散裂靶是耦合加速器与次临界堆的核心部件。中国加速器驱动嬗变研究装置(CiADS)中的散裂靶采用中国科学院ADS研究团队研发的固体颗粒流方案[17]。该方案以流动的固体颗粒为靶材，同时充当自身的冷却介质，与质子束流散裂反应产生中子的同时，利用其流动特性将高功率密度的束流沉积热带出束靶耦合的反应区，兼具了固态靶和液态靶的优势。颗粒流靶作为一种新概念散裂靶，尚处于设计阶段[18]，将颗粒流靶的模型简化成1个锥形漏斗，几何参数如图10所示。

分别采用DEM和MPM对靶区的颗粒流动进行模拟。颗粒材料模拟参数列于表1。t=0 s时漏斗内填满颗粒材料，流动开始后，颗粒材料会从漏斗入口不断注入。颗粒流经靶区后流出，在靶区会形成一个稳定流动的流场分布。两种方法模拟得到的稳定流动z方向速度分布如图11所示。图12为MPM计算得到的颗粒质量流量随时间变化的结果。可看出，当t=1 s时，流动趋于稳定，质量流量为285.43 kg/s，DEM的稳定质量流量为288.5 kg/s。

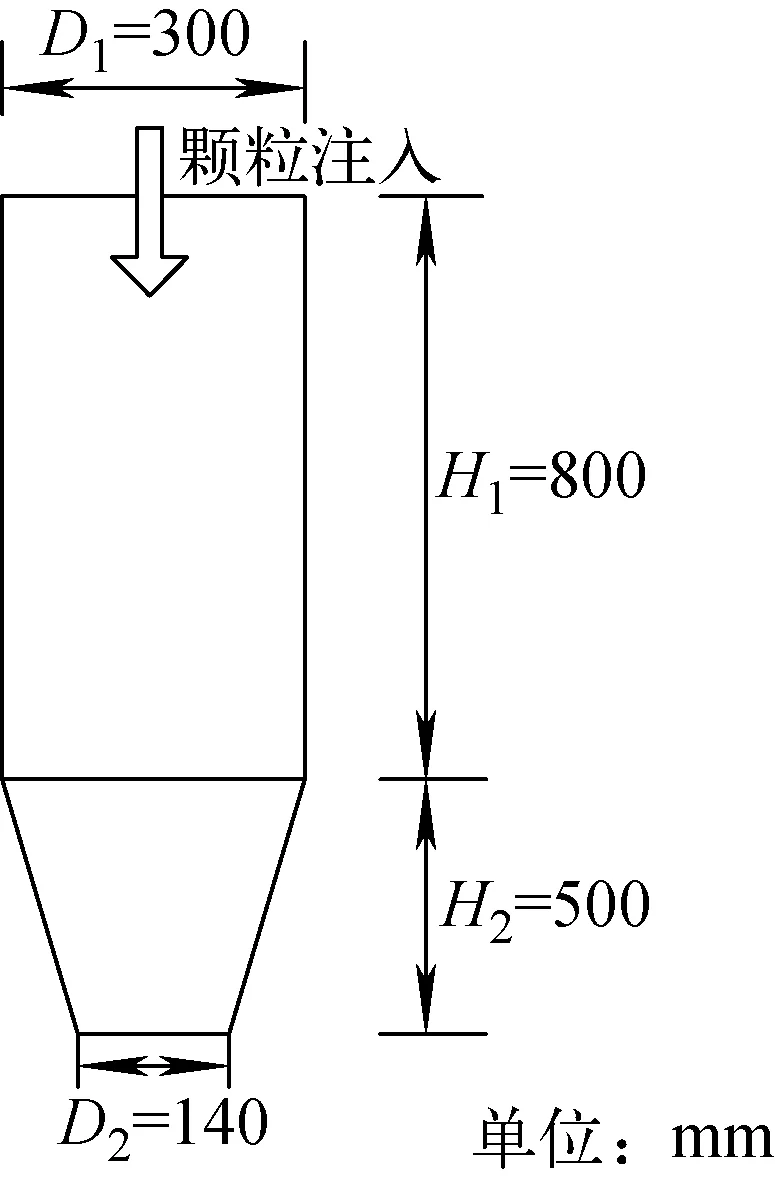
图10 颗粒流靶简化模型Fig.10 Geometrical model of granular flow target

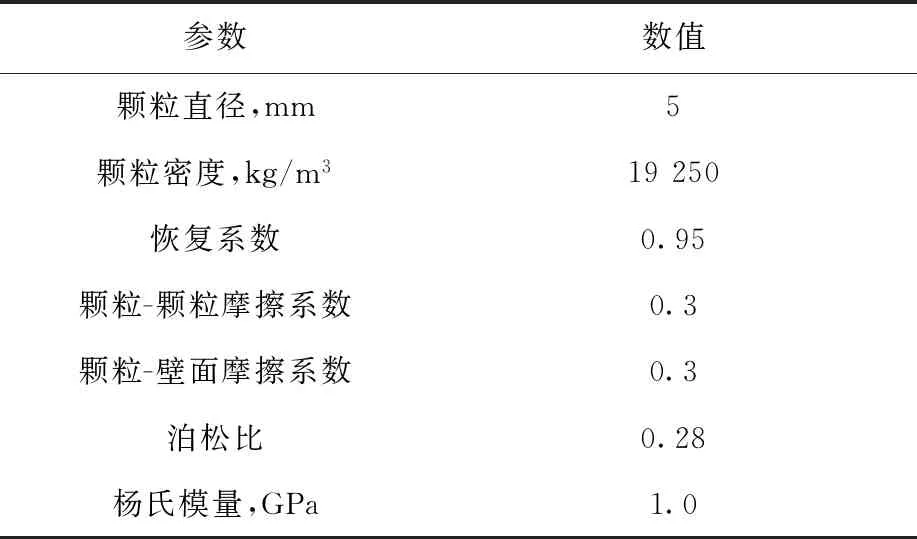
表1 颗粒流靶材料参数Table 1 Parameter for granular target

从图11a可看出，由于壁面的摩擦作用，靠近壁面的一层颗粒会有“贴壁”现象，在壁面处形成较大的速度梯度。连续性方法模拟出的结果在主流区能与DEM结果吻合较好，但在靠近壁面的边界处没有模拟出颗粒在壁面处的“贴壁”现象。分析原因有如下两点。

1) 连续性方法中，颗粒与壁面相互作用的理论模型不完善。颗粒与壁面之间的相互作用较复杂，目前大部分学者关注的仍为颗粒与颗粒之间的相互作用。对于颗粒与壁面的相互作用，目前的处理方式是给定屈服摩擦系数μw(μw为常数)，当壁面剪切力与压力的比值超过此值时，颗粒开始流动。这种处理方式过于简化，且DEM中颗粒与壁面的摩擦系数，与将颗粒视为连续体宏观上体现出来的与壁面之间的摩擦系数含义不同。关于DEM中颗粒-颗粒摩擦系数、颗粒-壁面摩擦系数与连续性方法中μ(I)流变模型参数、颗粒介质-壁面摩擦系数μw两套参数之间如何对应还需进一步研究。

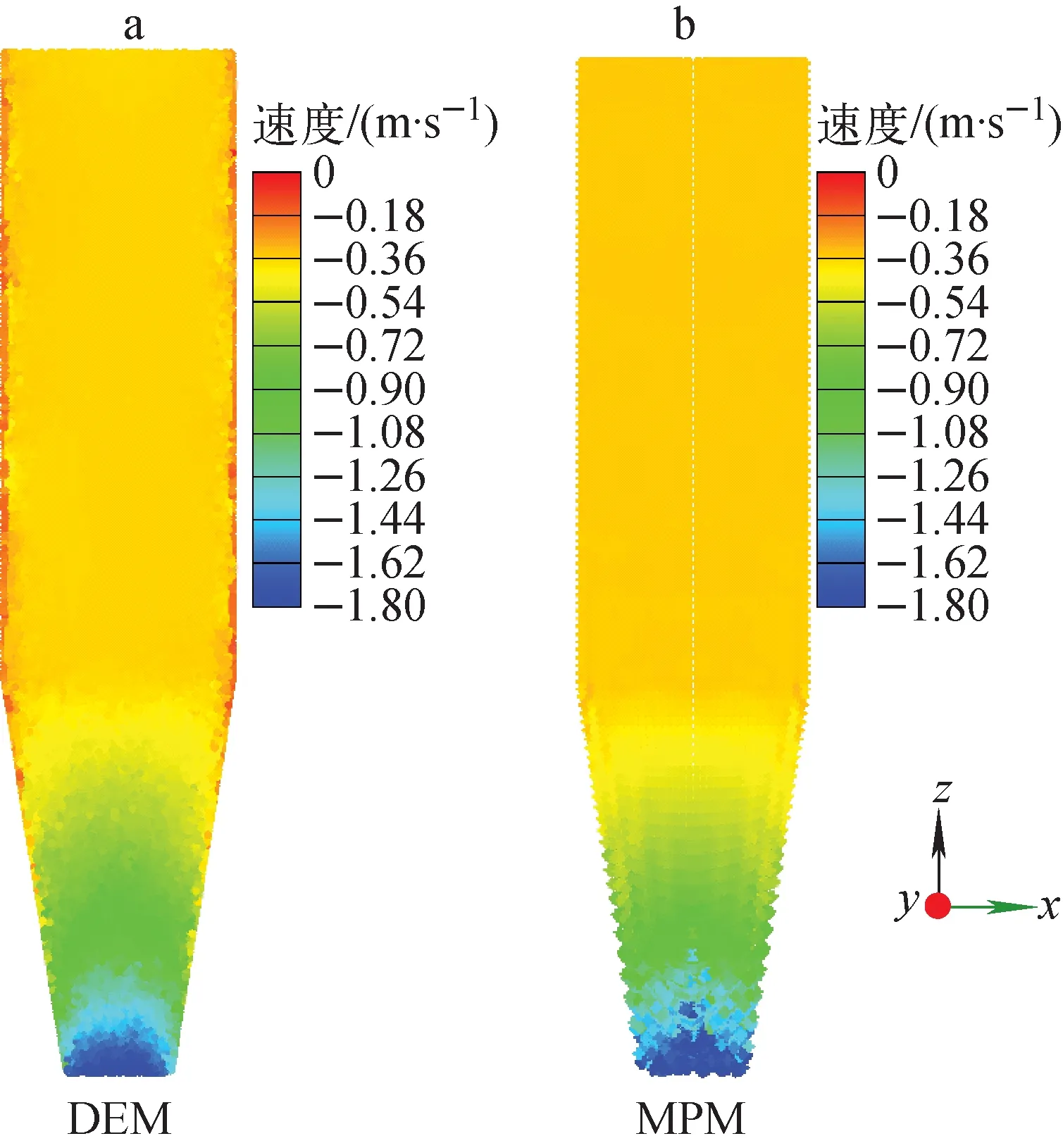
图11 颗粒流靶流动结果对比Fig.11 Velocity of granular flow target

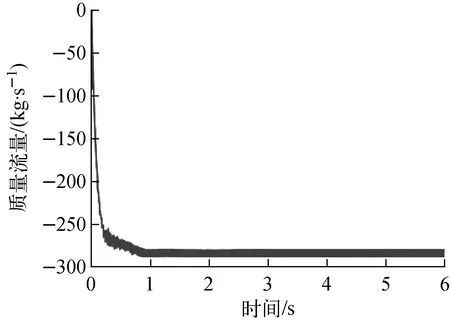
图12 MPM计算的质量流量随时间的变化Fig.12 Variation of mass flow rate calculated by MPM with time

2) MPM中接触算法不成熟。目前程序中处理颗粒与壁面的相互作用是将壁面视为刚体材料处理，考虑颗粒材料与刚体的相对滑动，需在物质点方法中引入接触算法。接触算法中，边界处约束过强会导致数值不稳定。

5 结论

1) 本文基于物质点方法，结合针对颗粒固态的弹塑性理论和适用于颗粒液态的μ(I)流变模型，实现了用连续性方法模拟密集颗粒流动的框架。

2) 在此框架下，模拟了颗粒介质坍塌流动，计算结果与物理实验和DEM模拟结果均吻合较好。

3) 对颗粒在重力驱动下漏斗中的流动进行了模拟，卸料率结果与Beverloo经验公式吻合较好。对于ADS颗粒流靶流动，主流区速度分布与DEM结果吻合较好，但无法模拟出壁面处颗粒的“贴壁”现象，经过分析认为这是颗粒与壁面相互作用的理论模型不完善以及MPM中接触算法不成熟导致的，这些问题需要在后续研究中加以解决。

4) 可在本文探究的连续性方法模拟密集颗粒流动框架的基础上，完善边界条件和本构模型，为用连续性方法处理大量颗粒的工程问题提供借鉴。

本文所用程序基于清华大学张雄教授所提供的开源三维物质点法程序(MPM3D)改编而成，文中的颗粒坍塌实验数据由清华大学水利系孙其诚老师提供，在此对两位老师一并表示感谢。