基于地理加权回归的地形平缓区土壤有机质空间建模
赵明松,刘斌寅,卢宏亮,李德成,张甘霖
基于地理加权回归的地形平缓区土壤有机质空间建模
赵明松1,2,刘斌寅1,卢宏亮1,李德成2,张甘霖2※
(1. 安徽理工大学测绘学院,淮南 232001;2. 土壤与农业可持续发展国家重点实验室中国科学院南京土壤研究所,南京 210008)
气候变化效应评估、土壤固碳潜力和肥力管理等,迫切需要详尽的土壤有机质(soil organic matter, SOM)空间分布信息。该文以江苏省第二次土壤普查的1 519个典型土壤剖面的表层(0~20 cm)SOM含量为例,选择1 217个样本为建模集,302个为验证集,选取年均温度、年均降雨、物理性黏粒和土壤pH值等因子进行SOM的地理加权回归(geographically weighted regression, GWR)建模。从建模集中分别随机抽取100%(1 217个)、80%(973个)、60%(730个)、40%(486个),20%(243个)的样点,对比不同样点数量下GWR和传统全局回归模型的精度差异,并选择最优模型进行SOM空间预测制图。结果表明:1)江苏省SOM含量在不同空间尺度上存在极显著的空间自相关性。不同样点数量的建模集的全局自相关性和局部空间自相关聚类图结果相似。全局Moran’s I值介于0.25~0.61(<0.001)。SOM含量空间分布以空间聚集特征为主,“高-高”聚集区主要分布在苏中和苏南地区,“低-低”聚集区主要分布在苏北地区。2)GWR建模结果均优于传统的全局回归建模,其残差在不同的空间尺度上均不存在空间自相关性。不同建模集的GWR的2adj较全局建模均提高0.15~0.20,其AIC和RSS均比全局模型有大幅降低,为56.08~360.19和17.40~76.67。不同建模样本数量的GWR模型对SOM的解释能力差异较小。3)建模样点数量(除建模样本=243)对GWR预测制图结果的精度影响不大,RMSE介于5.56~5.75 g/kg之间,MAE介于3.87~4.05 g/kg之间,2介于0.52~0.48之间,均优于全部建模样点的普通克里格插值验证结果。该研究可为样点数较少的省级尺度地区SOM空间建模与制图提供借鉴。
土壤; 有机质;模型;地理加权回归;数字土壤制图;地形平缓区;江苏省
0 引 言
土壤有机质(soil organic matter,SOM)是土壤肥力和质量的重要指标,是陆地生态系统碳储量的重要组成部分,在农业生产和环境保护等方面有着重要的意义[1-2]。研究SOM空间分布是评估区域土壤碳储量、实现土壤可持续利用的前提,也是土壤质量研究的重要内容。20世纪90年代兴起的计量土壤学和数字土壤制图研究,主要基于土壤-景观模型,利用土壤在地形、植被等景观环境上的差异,采用线性回归、广义线性回归、地统计学、模糊聚类、地理加权回归(geographically weighted regression, GWR)、机器学习等数学方法和地理信息系统等技术进行土壤属性的空间建模,为获取栅格化的土壤空间分布信息提供解决途径[3-8]。建立较优的土壤属性空间预测模型是获取较准确的土壤空间分布信息的关键。但是在平原或地形平缓地区,由于地形差异减小,植被等景观环境因素差异也变小,地形和植被等条件不能反映土壤的空间变异,因此不能有效地用于土壤属性的空间建模。
土壤是具有高度变异的时空连续体,在形成发育过程中成土因子对土壤的作用是非线性,在较大区域中土壤属性的主要影响因素较多,这种非线性作用更为明显。周涛等[9]研究发现在<10 ℃的地区,有机碳储量与年均温的负相关性最强;在10~20 ℃的地区,受与降水正相关的影响,有机碳储量与年均温呈正相关;而在>20 ℃的地区,有机碳储量与温度和降水的相关性都很差。赵明松等[10]研究表明江苏省土壤质地对SOM的作用在不同土壤类型和地理区域间存在着差异,总体上由北至南相关性减弱。因此在较大区域尺度上,利用传统的全局模型(如线性回归,普通回归克里格等)并不能很好地或较为准确地拟合环境因子与土壤属性之间的非线性关系。
GWR模型由英国地理学家Fotheringham等[11]提出,针对自变量和因变量间的关系在不同空间上的变化进行非参数局部空间回归建模,模型中自变量的回归系数随空间位置而变化,对于空间数据具有较强的局部分析能力[12-13]。GWR探测空间关系的非平稳性,广泛用于区域经济[14-16]、生态环境[17-20]、土壤建模制图[21-25]等研究。刘琼峰等[17]利用GWR模型分析了长沙城郊农田土壤Pb、Cd含量的空间结构及影响因素。郭龙等[26]等对比发现协同克里格和GWR模型在土壤预测制图中均具有较高精度。Zeng等[25]研究表明在小流域尺度和地区尺度上GWR模型均能提高SOM建模的精度。Song等[21]、Yang等[23]研究表明GWR模型能够提高较大复杂景观区域的土壤有机碳和电导率的建模预测精度。Zhang等[24]基于GWR模型利用年均降雨、土壤类型和土地利用等因子预测了爱尔兰全国的土壤有机碳的空间分布。上述研究表明了GWR模型在较大区域中土壤属性空间建模的优势。
针对较大区域尺度、地形平缓区土壤属性空间建模中存在的问题,以及省级尺度上采集大量土壤样品的困难。本研究选择江苏省为例,以第二次土壤普查数据为基础,选择栅格气象数据等,采用GWR模型开展地形平缓区SOM建模预测研究,并探讨样点数量对GWR建模精度的影响。研究结果可为省级尺度区域的SOM空间预测制图提供借鉴,为江苏省土壤肥力和质量管理、提升区域土壤固碳能力等提供数据基础。
1 材料与方法
1.1 研究区概况
江苏省(116°18′~121°57′ E,30°45′~35°20′ N)地处中国大陆东部,长江、淮河下游,面积10.26万km2。全省处于亚热带向暖温带过渡地带,年均气温13~16 ℃,年均降水量800~1 200 mm,年均日照2 100~2 600 h。全省平均海拔13 m,海拔低于10 m或坡度小于1%的区域占全省陆地面积的90%。按地质地貌差异,分为低山丘陵岗地区和平原区,平原、低山丘陵和水域面积分别占69%、14%和17%。低山丘陵分布在西南和东北部;平原由北至南为徐淮黄泛平原、里下河平原、滨海平原、沿江平原和太湖平原。主要的土壤类型有水稻土、潮土、砂姜黑土、滨海盐土、黄棕壤、黄褐土、棕壤等。水田和旱地分别占全省面积的42.46%和23.57%(2006年)。江苏省是中国重要的粮食生产基地,随着农业现代化和城市化的迅猛发展,土壤保护与利用之间的矛盾比较突出,对土壤空间分布信息的需求非常迫切。
1.2 数据来源
土壤数据来源于江苏省第二次土壤普查资料(1979-1982年)中记录的典型土壤剖面,主要包括《江苏土种志》[27]和各市、县土种志共60本。土壤剖面数据主要包括采样点位置和景观环境描述和土壤理化性质(主要有SOM、pH值、物理性黏粒和砂粒含量等),筛选出土壤数据比较完备的1 519个样点(图1)。本研究以表层(0~20 cm)SOM含量为研究对象。对于深度大于20 cm的土层数据不做处理,对于小于20 cm的土层,以土层深度为权重取0~20 cm内的所有土层的加权平均值。SOM含量采用重铬酸钾(K2Cr2O7)氧化-滴定法测定。
年均气温和年均降水量数据,来自中国农业科学院农业资源与农业区划研究所中国生态环境背景层面建造项目完成的栅格数据(1 km分辨率),为1980-1999年的逐月平均值计算合成。在ArcGIS软件中,根据地形图、行政区划变更信息等资料,将剖面点位置空间化,从气候栅格数据中提取各剖面点的年均气温和年均降水数据。
江苏省地形以平原为主,研究发现SOM含量与海拔和坡度等地形因子的相关性不足0.01,利用逐步回归建模分析时,无法进入模型,可用于SOM空间建模的有效变量较少。对于省级区域尺度,气候等条件对土壤属性的影响较大。鉴于以上背景和原因本文选择年均气温、年均降雨、物理性黏粒含量、土壤pH值等环境变量进行SOM含量的空间建模。

图1 土壤样点分布图
1.3 研究方法
1.3.1 地理加权回归
GWR模型的一般形式如下

式中(u,v)是第个样点的空间坐标;为验证样点个数;Y和X是因变量和自变量集X在空间位置(u,v)处的实测值;0(u,v)为在空间位置(u,v)处的常数项;系数(u,v)是连续函数(,)在点的值;为符合(0,2)分布的误差项。通常采用加权最小二乘法进行系数的局部估计。一般采用高斯(Gaussian)型或双重平方(bi-square)型空间核函数,利用空间位置(u,v)与周围一定距离(又称带宽)内观测样点的距离来估算其权重。本研究采用双重平方函数估算权重,采用黄金分割搜索(golden section search)方法、赤池信息量准则(akaike information criterion,AIC)[28],确定最优带宽,评价拟合模型的优劣。根据Fotheringham等[11]提出的方法准则,当GWR模型AIC值最小时,带宽b为最优带宽,此时模型拟合最优。详细的GWR模型拟合方法参考文献[11]。如果公式(1)中系数(,)在空间中任意一点保持不变,则为全局模型,即传统回归模型,通常用普通最小二乘法(ordinary least square, OLS)估计参数。
1.3.2 数据处理与分析
本研究采用相关性分析、回归分析等,研究年均气温、年均降雨、物理性黏粒、土壤pH值对江苏省SOM的影响,采用容差和方差膨胀因子(VIF)对环境因子与SOM关系进行共线性检验,在SPSS 18.0中完成。在利用GWR进行SOM空间建模时,选择302个样本作为验证集,1 217个样本为建模集。为比较不同样本数量下GWR建模的精度差异,从建模集中分别随机抽取100%(1 217个)、80%(973个)、60%(730个)、40%(486个),20%(243个)的样点进行建模,并选择最优模型进行SOM预测制图。利用ArcGIS 9.3的地统计模块中创建子集(create subsets)功能完成不同数量建模样本的抽样。利用GWR4.0软件进行GWR建模与制图。同时,利用ArcGIS 9.3的地统计模块以全部建模集(1 217个)进行普通克里格插值(ordinary kriging,OK),绘制SOM空间分布图与GWR预测制图结果做对比。
在SOM空间预测制图时,需要环境因子(建模的自变量)的空间分布。本研究中物理性黏粒含量和pH数据为点状数据,利用1 519个样点进行OK插值生成其空间分布,用于SOM空间制图。综合考虑气象数据的分辨率、研究区较大及数据运算等问题,制图结果均采用1 km空间分辨率。
1.3.3 模型评价
选取平均误差(mean error,ME)、平均绝对误差(mean absolute error,MAE)、均方根误差(root mean of squared error,RMSE)和决定系数(determination coefficient,2)等指标评价建模结果,其计算公式如下





2 结果与分析
2.1 SOM主要影响因素分析
江苏省SOM质量分数范围较大(= 1 519),为1.3~52.4 g/kg,极差为51.1 g/kg;平均为16.55 g/kg,标准差为8.49 g/kg(表1)。变异系数为51.36%,属于中等变异强度。偏度和峰度系数分别为1.12和1.75,经自然对数变换后符合正态分布。不同样点数量的建模集的SOM频率分布均符合对数正态分布。
相关分析表明,江苏省SOM与年均气温极显著正相关,相关系数为0.47(<0.001,=1 519),以年均降雨量为控制变量时二者的偏相关系数为0.21(<0.001,= 1 519),即在温度较高的长江以南地区SOM含量较高,温度较低的苏北地区含量较低。这与周涛等[9]、许信旺等[29]研究结果一致。SOM与年均降雨量极显著正相关,相关系数为0.44(<0.001,=1 519),以年均气温为控制变量时二者的相关性降低,偏相关系数为0.11(<0.001,=1 519)。这表明SOM与降雨量的相关性是由年均降雨与年均气温的相关性(=0.82,<0.001)引起的。SOM与土壤物理性黏粒和砂粒含量相关系数为0.46和−0.45(<0.001,=1 519)。SOM与pH值的相关系数为−0.30(<0.001,=1 519)。线性回归分析表明年均气温、年均降雨、土壤质地和pH值对SOM含量(=1 519)变异的综合解释能力为45.3%(0.001)。回归模型中的各因子的容差介于0.31~0.98,均大于0.1,VIF介于0.02~3.25,均不大于7.5,表明自变量之间不存在高度共线性[30]。
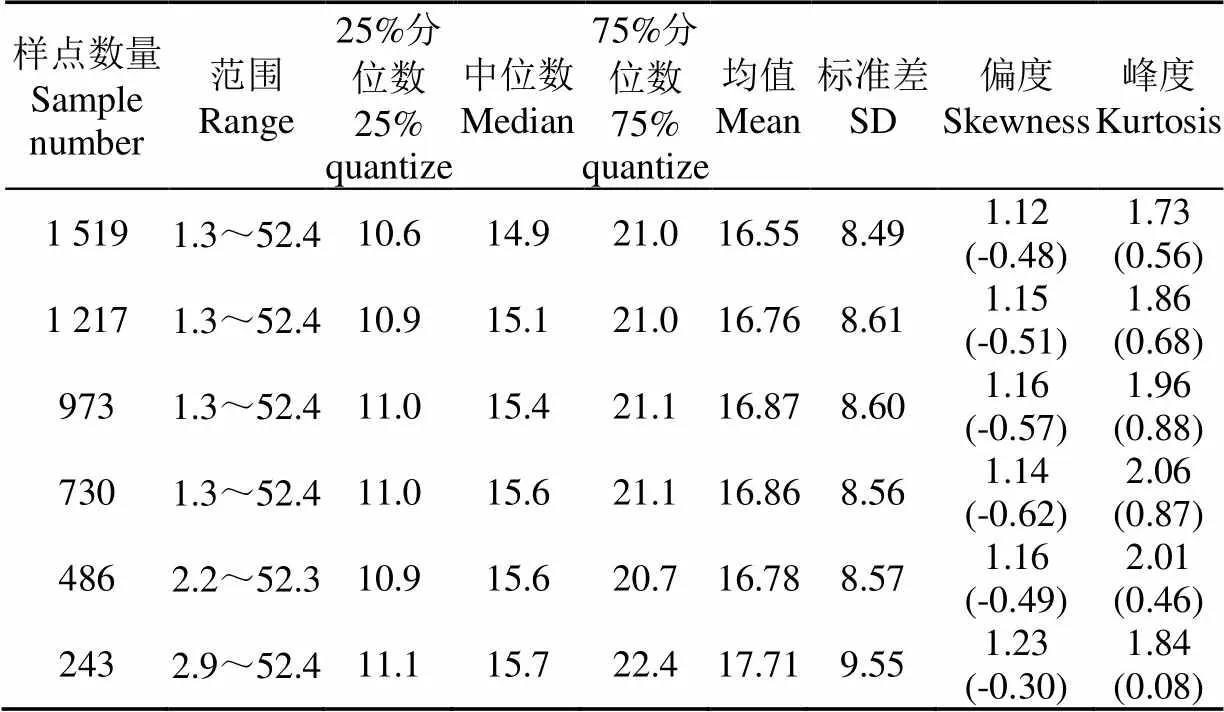
表1 江苏省SOM含量统计值
注:括号内为自然对数变换值。
Note: values in the brackets were logarithm transformed.
2.2 SOM空间自相关分析
利用ArcGIS软件空间统计功能分析不同建模样本集的SOM的全局和局部空间自相关性。在ArcGIS中计算全局Moran’s I值时,在0~100 km范围内按照10 km间隔设定不同的空间距离,计算全局Moran’s I值。图2为不同建模集的全局Moran’s I值,结果表明不同建模样本集的SOM在不同的空间尺度上均存在不同程度的极显著空间自相关性,全局Moran’s I值介于0.25~0.61(<0.001)。随着空间距离的增大,不同建模集的SOM的全局Moran’s I值均逐渐减小,表明其空间自相关性随着空间距离的增大而递减。在相同的空间距离上,除建模集为=486时的全局Moran’s I值稍小外,其他建模集的SOM的全局Moran’s I值总体上相差不大。
图3为建模集为=1 217时的局部空间自相关聚类图。由图知,江苏省SOM含量存在空间聚集特征,“高-高”(high-high)聚集区(SOM含量较高且空间差异较小的样点聚集分布)主要分布在苏中和苏南地区,“低-低”(low-low)聚集区(SOM含量较低且空间差异较小的样点聚集分布)主要分布在苏北地区;“高-低”(high-low)聚集区(SOM含量较高的样点被含量较低的样点包围,且含量的空间差异显著)主要分布在苏北地区,“低-高”(low-high)聚集区(SOM含量较低的样点被含量较高的样点包围,且含量的空间差异显著)主要分布在苏南地区。不同建模集的局部空间自相关聚类图结果相似,没有一一作图展示。以上分析表明不同建模集的SOM在不同的空间尺度均存在显著的全局和局部空间自相关性,可以采用GWR模型进行研究区SOM建模[17]。

注:显著性为P<0.001。

注:图例代表不同聚类聚集区,下同。
2.3 基于GWR的SOM建模分析
将不同建模集的SOM经过自然对数变换后,分别进行GWR建模和全局建模。为了比较不同自变量在建模中的贡献大小,首先在建模前将各自变量进行标准化变换到同一量纲,然后通过其系数来对比各自变量在SOM建模中的作用。
表2为不同建模集的SOM的GWR建模和全局建模结果。一般认为GWR模型和全局模型的AIC相差大于3,即使考虑到GWR模型的复杂性,其也明显优于全局模型。

表2 不同样点数量的GWR建模和全局建模结果比较
表2显示对于不同建模集的GWR模型的AIC均比相应的全局模型要小,相差56.08~360.19之间,表明GWR模型明显优于全局模型。不同建模集的GWR模型的调整决定系数(2adj)均大于相应的全局模型,其2adj较相应的全局模型增加0.15~0.20之间,表明对于相同的建模集,GWR模型对SOM变异的解释能力大于全局模型。对于不同建模集SOM的GWR模型,2adj介于0.54~0.62,总体上随着建模样本数量的减少GWR模型对SOM的解释能力稍有差异,但差异不大。这说明对于江苏省SOM的建模估计,采用较少样点数进行GWR建模时,也可满足一定的精度需求(如建模样本= 486和= 1 217的模型拟合度较接近)。对于不同建模集SOM的全局模型,其2adj介于0.39~0.44之间。
不同建模集的GWR模型的残差平方和(residual sum of squares,RSS)均比相应的全局模型减少17.40~76.67之间。GWR模型和全局模型残差的方差分析结果(表3)显示,不同建模集的GWR模型的残差较全局模型的残差显著降低,其检验值均达到0.01极显著性水平,表明GWR模型的拟合效果较全局模型有显著改善。上述这些结果表明,不同建模集的GWR建模结果均优于全局建模,且当建模样点数较少时GWR模型也能有较好的建模效果。
表4为不同样点数量的GWR模型回归系数和全局模型回归系数。结果显示,在不同样点数量的全局建模中(除样点数量= 243),同一环境因子对SOM预测的作用相似,如各全局模型中黏粒的回归系数介于0.24~0.25,相差较小;不同变量对SOM的作用大小依次为:黏粒> 年均温> 年均降雨> 土壤pH值。在不同样点数量的GWR建模中(除样点数量= 243),从回归系数的中值和平均值来看,各环境因子对SOM的作用大小规律与全局建模一致。当建模样点数量较少(= 243时),环境因子与SOM之间的关系不能完全地表达和刻画。GWR模型中,各环境因子的回归系数存在不同幅度的变化范围,同一环境因子的回归系数变化范围相差不大,其中黏粒的回归系数变化范围最稳定且系数均为正(表4),体现了黏粒含量对SOM含量的正相关。

表3 GWR模型和全局建模残差的方差分析结果
注:**为显著性< 0.01,下同。
Note: **is significant difference at 0.01 level, the same below.
图4为GWR模型回归系数(建模样点= 1 217),各环境因子对SOM的作用存在显著的空间差异,即SOM与这些环境因子之间的关系存在空间非平稳性[19]。各因子对SOM的影响程度可通过对应的回归系数来解释,回归系数的绝对值大小反映该因子对SOM影响的强烈程度,正反映因子对SOM的正影响或正相关,反之亦然[13, 30]。如,黏粒的回归系数变化范围比其他因素回归系数的变化范围较小,表明在研究区内黏粒对SOM的影响相比其他因素较稳定。黏粒对SOM的影响在江苏省东北部和西南部最小,在中南部最大,且均表现为正的影响(图4a),这与赵明松等[10]在该地区的研究结果相似。年均温对SOM的作用在大部分地区表现为正相关(图4b);年均降雨对SOM的作用在江苏省东部地区表现为负相关,在西部表现为正相关。虽然研究区内年均温和年均降雨显著正相关,但是对于SOM的作用强度在空间上显著差异,相应系数的空间格局差异较大。土壤pH值对SOM的作用,在西北-东南方向上向南北两侧逐渐变化,总体上由负相关转变为正相关。
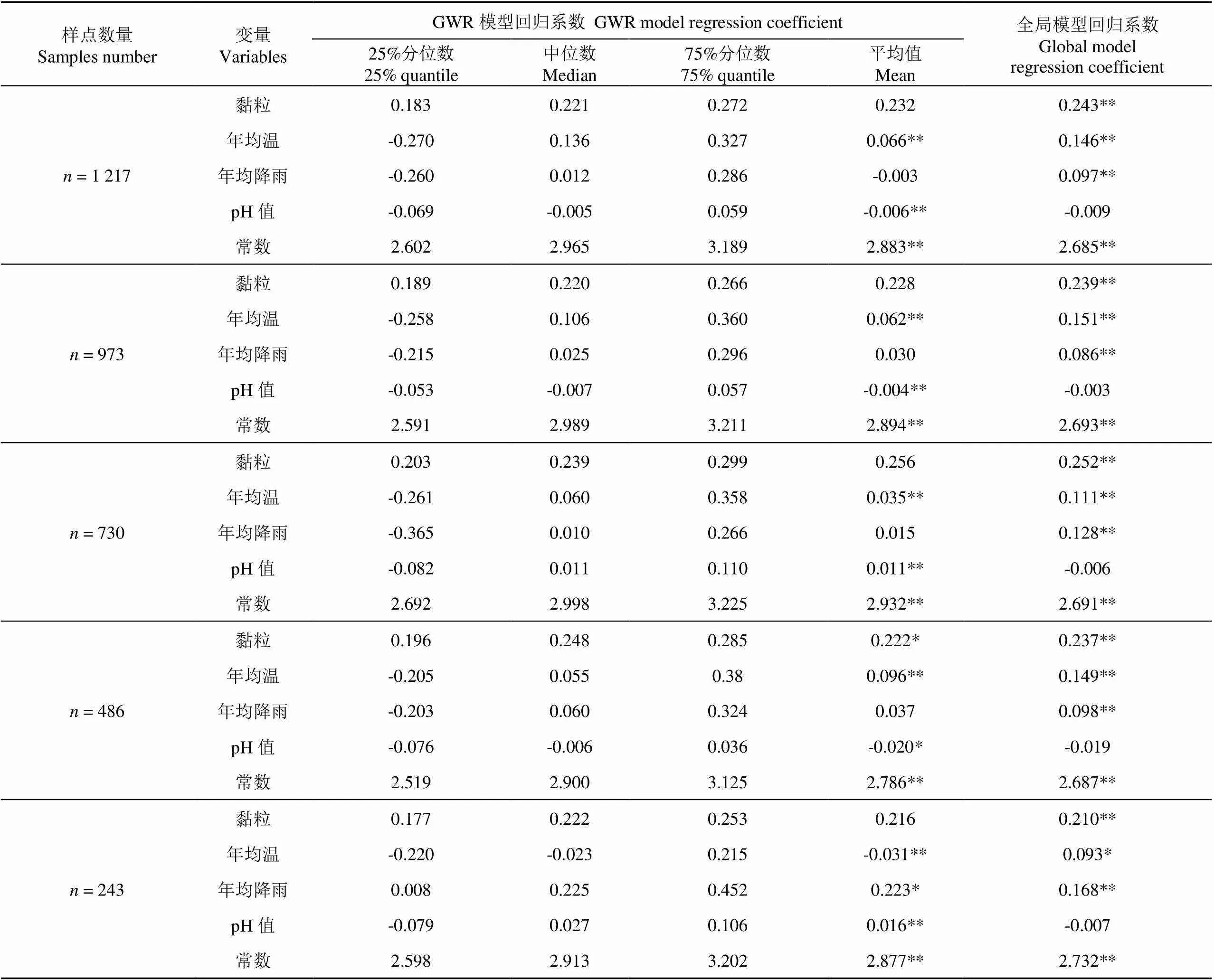
表4 不同样点数量的GWR模型回归系数
注:*显著性< 0.05,下同。
Note: *, ** Siginificant difference at 0.05 level, the same below.
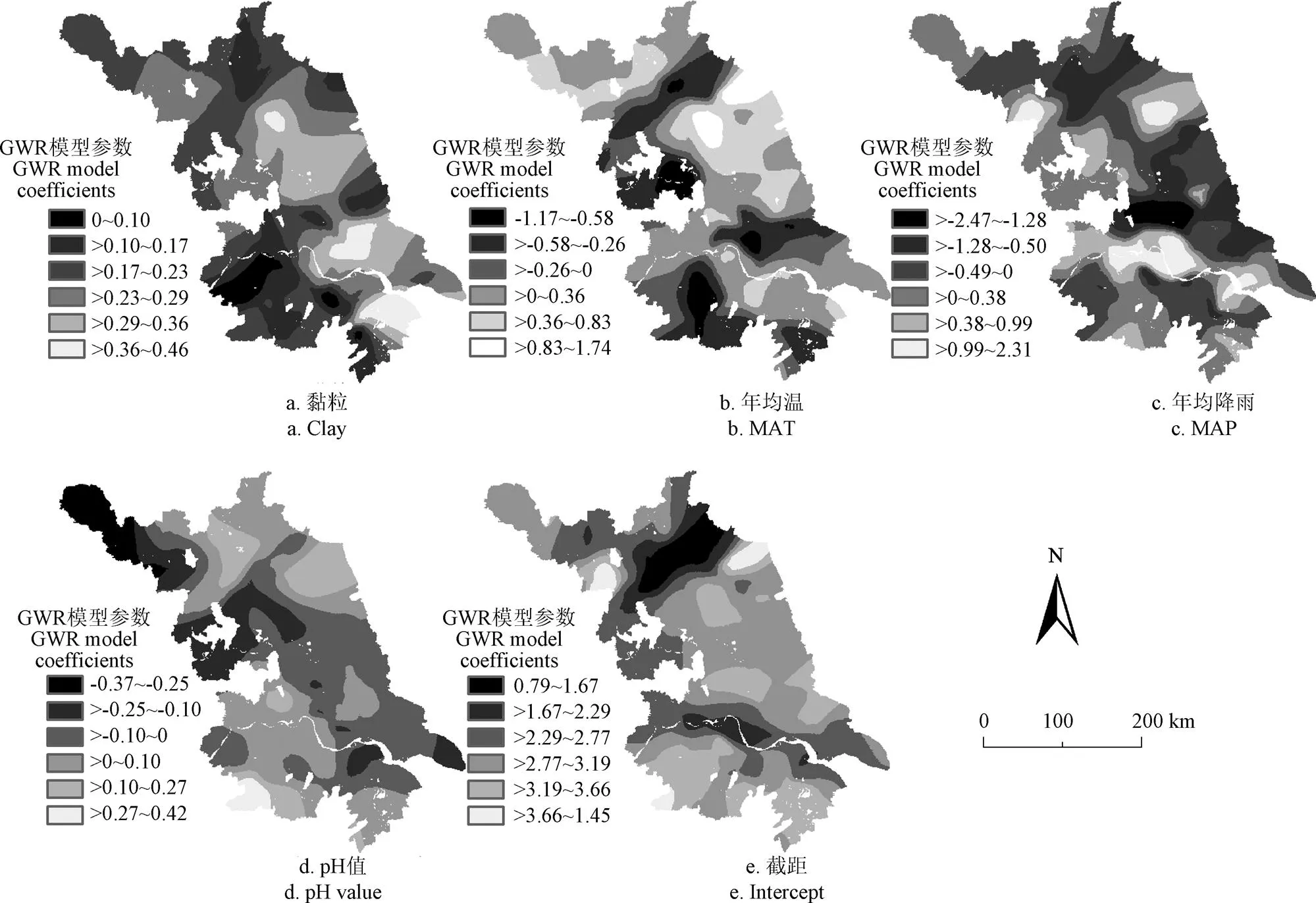
图4 GWR建模回归系数空间分布图(n=1 217)
2.4 基于GWR的SOM预测制图及模型评价
图5为江苏省SOM含量空间分布预测图,其中a~e为不同样点数量的GWR建模预测图,f为采用全部建模样点(=1 217)的OK插值图。

图5 SOM含量空间分布预测图
SOM的OK插值的变异函数采用球状模型拟合,块金值为0.13,偏基台值为0.10,变程为75 km,步长为10 km。结果显示,不同样点数量的GWR预测结果的范围介于3.38~45.08 g/kg,平均值介于14.94~15.34 g/kg,标准差介于5.99~7.15 g/kg,均比建模样点的相应统计值稍小。不同样点数量的GWR预测结果的空间分布格局基本一致:SOM含量的最高值主要分布在太湖平原和里下河平原,从苏南到苏北地区逐渐降低;在研究区西南部的部分地区SOM的空间分布细节存在细微差异(图5)。总体上,不同样点数量的GWR预测结果与采用全部建模样点的OK预测结果具有较相似的空间分布格局。
表5为SOM建模的独立验证结果。不同样点数量(除= 243时)的GWR建模的验证结果差异不大:RMSE介于5.56~5.75 g/kg,MAE介于3.87~4.05 g/kg,均小于全部建模样点的OK验证结果;2介于0.48~0.52,均高于OK插值的验证结果。不同样点数量的GWR验证结果的ME介于−0.58~−0.22 g/kg,表明GWR建模结果总体上存在不同程度的高估现象。样点数=243时GWR建模的验证结果(RMSE=6.31,ME=−0.22,MAE=4.47)较其他稍差,但其预测的空间分布格局与其他结果较相似。上述结果表明,在江苏省利用GWR进行SOM空间预测制图时,样点数量对建模精度影响不大,较少的样点数量也可以获得较好的制图结果。与OK插值方法比较发现,在样点数最大时,GWR建模精度提高幅度有限,2仅提高了0.06。但从另一个方面看,如果样点较少时(如486个)采用GWR建模,能够获得和较多样点的OK插值结果的相似精度,对减少制图成本也有一定的贡献。

表5 不同样本数量的GWR建模的验证结果
图6为不同样本数量的GWR模型残差的全局Moran’I指数。GWR模型残差的全局Moran’s I值介于0.01~0.12(>0.1),随着空间距离的增大其值均逐渐减小,表明在不同的空间尺度上不同样点数量的GWR模型残差均不存在显著空间自相关性。在相同的空间距离上,GWR残差的全局Moran’s I值总体上相差不大。图7为GWR模型残差(= 1 217)的局部空间自相关聚类图。由图知,绝大部分样点的建模均不存在显著局部空间自相关性,仅有少量样点(= 45)的残差存在着“高-高”(残差较高且空间差异较小的样点聚集分布区)、“低-低”和“高-低”聚类。不同建模集的GWR残差的局部空间自相关聚类图结果相似,没有一一作图展示。不同样点数量GWR建模的残差空间自相关性较弱,也间接表明GWR拟合的模型较优。

注:不显著(P=0.1)。
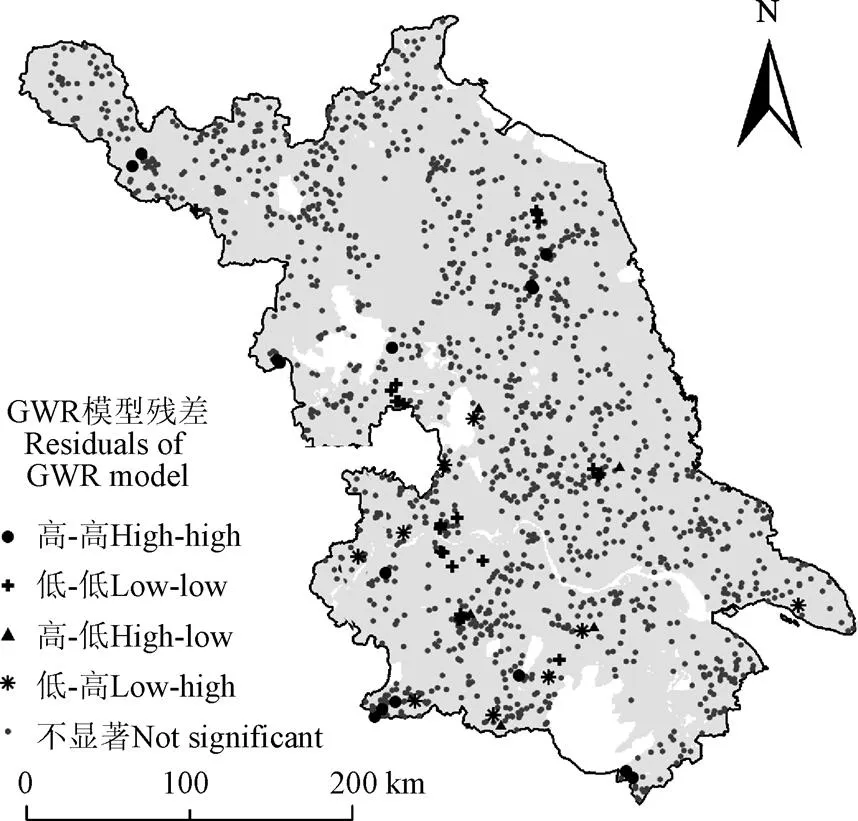
图7 GWR模型残差局部空间聚类图(n=1 217)
3 结 论
1)江苏省SOM含量在不同空间尺度上存在极显著的全局和局部空间自相关性。SOM含量空间分布以空间聚集特征为主,“高-高”聚集区主要分布在苏中和苏南地区,“低-低”聚集区主要分布在苏北地区。不同建模集的全局自相关性和局部空间自相关聚类图结果相似。
2)GWR建模结果均优于全局建模,对SOM空间变异的解释能力更高,不同建模集的GWR的2adj较全局建模均有明显提高,其AIC和RSS均比全局模型有大幅降低,拟合效果有较大提升。随着建模样本数量的减少GWR模型对SOM的解释能力差异不大。GWR建模的残差在不同的空间尺度上均不存在空间自相关性。
3)利用GWR模型进行SOM空间预测制图时,建模样点数量对建模精度影响不大,不同样点数量的GWR建模结果与采用全部样点的OK插值结果具有相似的空间格局。样点数较少时,在大区域利用GWR模型进行SOM预测制图,也可以达到一定的精度要求。
数字土壤制图过程中,一般要求环境因子为空间栅格形式。本文中物理性黏粒含量和pH值为点状数据,在预测制图中首先通过插值其空间分布,再用于SOM预测制图,可能增加二次误差,对最终的制图结果可能会有一定程度的影响,这些有待进一步的深入研究。
[1] Yadav V, Malanson G. Progress in soil organic matter research: Litter decomposition, modelling, monitoring and sequestration [J]. Progress in Physical Geography, 2007, 31(2): 131-154.
[2] Davidson E A, Trumbore S E, Amundson R. Biogeochemistry: Soil warming and organic carbon content[J]. Nature, 2000, 408(6814): 789-790.
[3] McBratney A B, Santos M L M, Minasny B. On digital soil mapping [J]. Geoderma, 2003, 117: 3-52.
[4] Thompson J A, Pena-Yewtukhiw E M, Grove J H. Soil-landscape modeling across a physiographic region: Topographic patterns and model transportability [J]. Geoderma, 2006, 133: 57-70.
[5] Qi F, Zhu A X, Harrower M, et al. Fuzzy soil mapping based on prototype category theory[J]. Geoderma, 2006, 136: 774-787.
[6] Zhu A X, Qi F, Moore A, et al. Prediction of soil properties using fuzzy membership values [J]. Geoderma, 2010, 158: 199-206.
[7] de Bruin S, Stein A. Soil-landscape modelling using fuzzy c-means clustering of attribute data derived from a digital elevation model (DEM) [J]. Geoderma, 1998, 83: 17-33.
[8] 朱阿兴,杨琳,樊乃卿,等. 数字土壤制图研究综述与展望[J]. 地理科学进展,2018,37(1):66-78.
Zhu Axing, Yang Lin, Fan Naiqing, et al. The review and outlook of digital soil mapping[J]. Progress in Geography, 2018, 37(1): 66-78. (in Chinese with English abstract)
[9] 周涛,史培军,王绍强. 气候变化及人类活动对中国土壤有机碳储量的影响[J]. 地理学报,2003,58(5):727-734.
Zhou Tao, Shi Peijun, Wang Shaoqiang. Impacts of climate and human activities on soil carbon storage in China[J]. Acta Geographica Sinica, 2003, 58(5): 727-734. (in Chinese with English abstract)
[10] 赵明松,张甘霖,李德成,等. 江苏省土壤有机质变异及其主要影响因素[J]. 生态学报,2013,33(16):5058-5066.
Zhao Mingsong, Zhang Ganlin, Li Decheng, et al. Variability of soil organic matter and its main factors in Jiangsu Province[J]. Acta Ecologica Sinica, 2013, 33(16): 5058-5066. (in Chinese with English abstract)
[11] Fotheringham A S, Brunsdon C, Charlton M. Geographically Weighted Regression—the Analysis of Spatially Varying Relationships[M]. Chichester.UK: John Wiley & Sons Inc., 2002: 42-46.
[12] 王远飞,何洪林. 空间数据分析方法[M]. 北京:科学出版社,2007:132-141.
[13] 瞿明凯,李卫东,张传荣,等. 地理加权回归及其在土壤和环境科学上的应用前景[J]. 土壤,2014,46(1):15-22.
Qu Mingkai, Li Weidong, Zhang Chuanrong, et al. Geographically weighted regression and its application prospect in soil and environmental sciences[J]. Soils, 2014, 46(1): 15-22. (in Chinese with English abstract)
[14] 吕萍,甄辉. 基于GWR模型的北京市住宅用地价格影响因素及其空间规律研究[J]. 经济地理,2010,30(3):472-478.
Lü Ping, Zhen Hui. Affecting factors research of Beijing residential land price based on GWR model[J]. Economic Geography, 2010, 30(3): 472-478. (in Chinese with English abstract)
[15] 汤庆园,徐伟,艾福利. 基于地理加权回归的上海市房价空间分异及其影响因子研究[J]. 经济地理,2012,32(2):52-58.
Tang Qingyuan, Xu Wei, Ai Fuli. A GWR based study on spatial pattern and structural determinants of Shanghai’s housing price[J]. Economic Geography, 2012, 32(2): 52-58. (in Chinese with English abstract)
[16] 刘卫东,刘红光,范晓梅,等. 地区间贸易流量的产业:空间模型构建与应用[J]. 地理学报,2012,67(2):147-156.
Liu Weidong, Liu Hongguang, Fan Xiaomei, et al. Sector-specific spatial statistic model for estimating inter-regional Trade tflows: A case study of agricultural, chemical and electronic sectors in China[J]. Acta Geographica Sinica, 2012, 67(2): 147-156. (in Chinese with English abstract)
[17] 刘琼峰,李明德,段建南,等. 农田土壤铅、镉含量影响因素地理加权回归模型分析[J]. 农业工程学报,2013,29(3):225-234.
Liu Qiongfeng, Li Mingde, Duan Jiannan, et al. Analysis on influence factors of soil Pb and Cd in agricultural soil of Changsha suburb based on geographically weighted regression model [J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2013, 29(3): 225-234. (in Chinese with English abstract)
[18] 霍霄妮,李红,孙丹峰,等. 北京耕地土壤重金属空间自回归模型及影响因素[J]. 农业工程学报,2010,26(5):78-82.
Huo Xiaoni, Li Hong, Sun Danfeng, et al. Spatial autogression model for heavy metals in cultivated soils of Beijing[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2010, 26(5): 78-82. (in Chinese with English abstract)
[19] 李锦芬,瞿明凯,黄标,等. 区域土壤CEC与相关控制因子的空间非平稳关系评估[J]. 土壤学报,2017,54(3):639-647.
Li Jinfen, Qu Mingkai, Huang Biao, et al. Spatially non-stationary relationships between cation exchange capacity and related control factors[J]. Acta Pedologica Sinica, 2017, 54(3): 639-647. (in Chinese with English abstract)
[20] 王景雷,康绍忠,孙景生,等. 基于PCA和GWR的作物需水量空间分布估算[J]. 科学通报,2013,58(12):1131-1139.
Wang Jinglei, Kang Shaozhong, Sun Jingsheng, et al. Estimation of crop water requirement based on principal component analysis and geographically weighted regression[J]. China Science Bulletin, 2013, 58, 1131-1139. (in Chinese with English abstract)
[21] Song X D, Brus D J, Liu F, et al. Mapping soil organic carbon content by geographically weighted regression: A case study in the Heihe River Basin, China[J]. Geoderma, 2016, 261: 11-22.
[22] Mishra U, Lal R, Liu D S, et al. Predicting the spatial variation of the soil organic carbon pool at a regional scale[J]. Soil Science Society of America Journal, 2010, 74(3): 906-914.
[23] Yang S H, Liu F, Song X D, et al. Mapping topsoil electrical conductivity by a mixed geographically weighted regression kriging: A case study in the Heihe River Basin, northwest China[J]. Ecological Indicators, 2019, 102: 252-264.
[24] Zhang C S, Tang Y, Xu X L, et al. Towards spatial geochemical modelling: Use of geographically weighted regression for mapping soil organic carbon contents in Ireland[J]. Applied Geochemistry, 2011, 26(7): 1239-1248.
[25] Zeng C, Yang L, Zhu A X, et al. Mapping soil organic matter concentration at different scales using a mixed geographically weighted regression method[J]. Geoderma, 2016, 281: 69-82.
[26] 郭龙,张海涛,陈家赢,等. 基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较[J]. 土壤学报,2012,49(5):1037-1042.
Guo Long, Zhang Haitao, Chen Jiaying, et al. Comparison between cokring model and geographically weighted regression model in spatial prediction of soil attributes[J]. Acta Pedologica Sinica, 2012, 49(5): 1037-1042. (in Chinese with English abstract)
[27] 江苏省土壤普查办公室. 江苏土种志[M]. 南京:江苏科学技术出版社,1996:5-105.
[28] Akaike H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723.
[29] 许信旺,潘根兴,汪艳林,等. 中国农田耕层土壤有机碳变化特征及控制因素[J]. 地理研究,2009,28(3):601-612.
Xu Xinwang, Pan Genxing, Wang Yanlin, et al. Research of changing characteristics and control factors of farmland topsoil organic carbon in China[J]. Geographical Research, 2009, 28(3): 601-612. (in Chinese with English abstract)
[30] 许尔琪. 基于地理加权回归的石漠化影响因子分布研究[J]. 资源科学,2017,39(10):1975-1988.
Xu Erqi. Spatial variation in drivers of karst rocky desertification based on geographically weighted regression model[J]. Resources Science, 2017, 39(10): 1975-1988. (in Chinese with English abstract)
Spatial modeling of soil organic matter over low relief areas based on geographically weighted regression
Zhao Mingsong1,2, Liu Binyin1, Lu Hongliang1, Li Decheng2, Zhang Ganlin2※
(1.232001; 2.210008)
Accurate estimates of the spatial variability of soil organic matter (SOM) are necessary to properly evaluate climatic chagne, soil carbon sequestration potential and soil fertility. In plains and gently undulating terrains, soil spatial variability is not closely related to relief, and thus digital soil mapping (DSM) methods based on soil-landscape relationships often fail in these areas. Therefore, different predictors or methods are needed for DSM in plains. In provincial regional scale, climatic factors influence spatial distribution of soil properties. For this research, Jiangsu Province was selected as example and mean annual temperature (MAT), mean annual precipitation (MAP), physical clay content, and soil pH were selected for SOM spatial modeling using geographically weighted regression (GWR). The SOM content in the surface layer (0-20cm) of 1 519 typical soil profiles of the Second National Soil Survey in Jiangsu Province were collected. 1 217 samples were selected as the modeling set and 302 were the validation set. Fristly, 100% (1 217), 80% (973), 60% (730), 40% (486), and 20% (243) samples were randomly selected from the modeling set, and global and local spatial autocorrelation of SOM content were analyzed at different spatial scales using spatial statistics tools in ArcGIS. Secondly, comparison of the accuracy between GWR model and the global regression model under the different sampling size was conducted. Akaike information criterion (AIC), residual sum of squares (RSS) and adjustment determination coefficient (2adj) were used modeling comparison. Thirdly, the optimal model was selected for mapping SOM spatial prediction. Independent validation was used for model evaluation, using four indices: mean error (ME), mean absolute error (MAE) and root mean of squared error (RMSE), and determination coefficient (2). Results show that: 1) There was a significant spatial autocorrelation of SOM content in Jiangsu Province at different spatial scales. The clustering pattern of global and local spatial autocorrelation of modeling set with different sampling size were similar. The global Moran’s I ranged from 0.25 to 0.61 (<0.001). The spatial distribution of SOM content was mainly characterized by spatial clustering pattern. The “high-high” clustering areas were mainly distributed in the central and south of Jiangsu, and the “low-low” clustering areas were mainly distributed in the north of Jiangsu. 2) The modeling results of GWR were better than the global regression modeling, and the residuals had no spatial autocorrelation at different spatial scales. The2adjof GWR in different modeling sets was increased by 0.15 to 0.20 compared with the global model. The AIC and RSS were significantly lower than the global model, which were decreased by 56.08 to 360.19 and 17.40 to 76.67 respectively. There were slight difference between GWR models with different sampling size. 3) The number of modeling samples (except for the number of modeling samples was 243) had little effect on the accuracy of prediction and mapping results of GWR, the RMSE was between 5.56 and 5.75 g/kg, MAE was between 3.87 and 4.05 g/kg and2was between 0.48 and 0.52. The results were all better than the validation result of Ordinary Kriging using all modeling sampling points. This study can provide reference for SOM modeling and mapping in large and low relief areas with sparse samples.
soils; organic matter; models; geographically weighted regression; digital soil mapping; low relief areas; Jiangsu Province
赵明松,刘斌寅,卢宏亮,李德成,张甘霖. 基于地理加权回归的地形平缓区土壤有机质空间建模[J]. 农业工程学报,2019,35(20):102-110.doi:10.11975/j.issn.1002-6819.2019.20.013 http://www.tcsae.org
Zhao Mingsong, Liu Binyin, Lu Hongliang, Li Decheng, Zhang Ganlin. Spatial modeling of soil organic matter over low relief areas based on geographically weighted regression[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(20): 102-110. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.20.013 http://www.tcsae.org
2019-03-26
2019-06-23
国家自然科学基金(41501226);土壤与农业可持续发展国家重点实验室开发基金(Y412201431);安徽省高校自然科学研究项目(KJ2015A034)
赵明松,博士,副教授,主要从事数字土壤制图和空间变异研究。Email:zhaomingsonggis@163.com
张甘霖,博士,研究员,博士生导师,主要从事土壤发生分类、土壤地理研究。Email:glzhang@issas.ac.cn
10.11975/j.issn.1002-6819.2019.20.013
S159.9
A
1002-6819(2019)-20-0102-09

