基于Green-Ampt的膜孔灌三维入渗模型建立与验证
费良军,康守旋,聂卫波,钟 韵,姜瑞瑞,陈 琳
基于Green-Ampt的膜孔灌三维入渗模型建立与验证
费良军,康守旋,聂卫波,钟 韵,姜瑞瑞,陈 琳
(西安理工大学西北旱区生态水利工程国家重点实验室培育基地,西安 710048)
在膜孔灌入渗方面研究中的入渗模型缺少明确的物理意义,针对这一问题,该文以一维Green-Ampt公式为基础进行探讨。对公式中概化湿润锋为平面的假设条件进行深化讨论,结合膜孔灌三维入渗特点,建立了包含膜孔直径、表征导水率和湿润锋面水吸力的膜孔灌入渗模型,利用室内入渗试验和以不同土壤质地(典型砂壤土、典型壤土和典型粉壤土)的Hydrus-2D软件数值模拟结果对其进行验证。结果表明:试验观测和数值模拟得到的单位面积累积入渗量随时间的变化规律与模型计算得出的结果一致,二者均方根误差和平均绝对误差接近于0,偏差百分比小于10%,数值相差不大;由模型计算得出的概化湿润锋由试验及模拟结果在入渗前期相差很小,在入渗后期差别逐渐变大;另外,相较于水平方向,垂直方向的概化湿润锋计算结果更加接近试验观测值和数值模拟值。建立的模型可为准确计算膜孔灌累积入渗量、预测湿润锋形状提供依据。
数值分析;入渗;土壤;膜孔灌;Green-Ampt模型;湿润锋
0 引 言
Green-Ampt公式是由Green和Ampt结合毛管理论,提出的土壤水分一维入渗公式[1],通常用来研究均质、干燥且表层有薄层积水的土壤水分入渗问题。该公式在基于一些基本假定的前提下推导而得到,其中物理量具有明确的物理意义,并具有参数少和求解简单等特点,因而在国内外得到了广泛的使用[2-5]。国内外学者对Green-Ampt公式中参数的确定进行了大量的研究工作,Bouwer[6]对公式中导水率的取值进行了研究,并提出公式中导水率取0.5倍的饱和导水率;张光辉等[7]以van-Genuchten导水模型为基础,利用模型中土壤物理参数推导出Green-Ampt公式中土壤水吸力的计算公式。针对不同的土壤入渗条件,一些学者对Green-Ampt公式进行了改进:马娟娟等[8]在研究变水头入渗时,在Green-Ampt公式中引入了湿润区平均含水率的概念,建立了有物理含义的3种入渗模型;王全九等[9]在研究层状土和浑水入渗时分别得出了2种不同形式的Green-Ampt公式,并结合2种入渗的特点对公式中的参数进行了讨论。随着灌水技术的发展,越来越多的灌溉方式被开发并日趋成熟,如膜孔灌灌水技术。膜孔灌入渗为三维入渗,而传统的Green-Ampt公式为一维入渗公式,基于Green-Ampt公式并结合膜孔灌入渗特性推导得到入渗模型对生产实践具有重要的意义。
膜孔灌是指灌溉水流在所覆地膜上流动,通过专门的作物放苗孔或者膜孔渗入到作物计划湿润层的灌水技术[10]。膜孔灌既是地面灌溉,又属于局部灌溉,因此其既具有节能的优点、又兼具局部灌溉的节水效果[11]。目前学者们对膜孔灌已有大量的研究[12-14]:费良军等[15]研究了膜孔灌单点源入渗单位面积侧渗量和一维垂直入渗量之间的关系,建立了包含二者的2个数学模型;马孝义等[16]利用SWMS-3D软件模拟不同土质、容积密度下膜孔灌单点源入渗,并提出了膜孔灌平均入渗水深的简化模型;范严伟等[17]将膜孔灌入渗量分为垂直入渗量和膜孔侧渗量,并引入单位膜孔周长侧渗量概念;钟韵等[18]采用多元回归法分析了土壤容重、初始含水率、压力水头等5个因素对膜孔灌入渗特性的综合影响。迄今为止,学者们对Green-Ampt公式和膜孔灌分别进行了大量的研究,但对膜孔灌条件下,基于Green-Ampt公式的入渗模型鲜有成果,因此本文就此问题进行了探究,以期为完善膜孔灌理论研究提供基础。
1 基本理论
1.1 一维Green-Ampt入渗公式
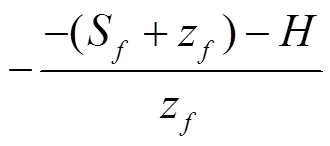
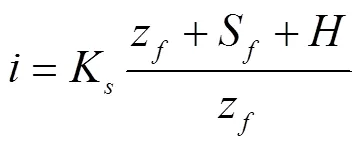
式中为入渗率,cm/min;K为表征导水率,cm/min;z为概化湿润锋深度,cm;S为湿润锋面处水吸力,cm;为土壤表层积水深度,cm。
由水量平衡原理知:
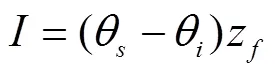
式中为累积入渗量,cm;θ为土壤饱和含水率,cm3/cm3;θ为土壤初始含水率,cm3/cm3。
入渗率和累积入渗量存在函数关系为

式中为时间,min。
式(1)-式(3)为Green-Ampt入渗公式,对于着重研究土壤入渗过程,Green-Ampt入渗公式具有特殊的作用。此公式因其各符号有着明确的物理量含义以及在使用过程中具有较高的准确性而受到广泛的应用。
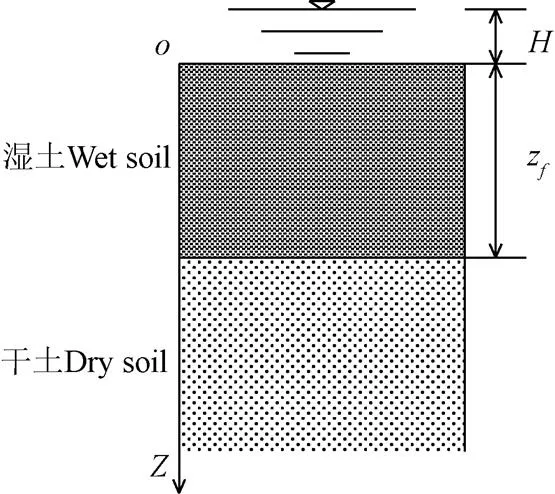
注:zf为概化湿润锋深度,cm;H为土壤表层积水深度,cm。
1.2 膜孔灌三维入渗模型的建立
1.2.1 膜孔灌入渗
膜孔灌入渗为三维入渗问题,如图2a所示,膜孔为具有恒定水头的圆柱形水室,其湿润体过膜孔中心的各个垂直剖面均相同。如图3为过膜孔中心的垂直剖面,其形状接近于1/2椭圆[20-21],因此整个湿润体形状为接近于以垂直剖面绕轴旋转后的旋转椭球体。为了研究方便,这里仅取过膜孔中心的垂直剖面研究。图2b所示垂直剖面中轴取向下为正方向,并设土层表面为轴起点,轴为土壤表层,轴与轴交点点为膜孔中心处。过膜孔中心的各个垂直剖面均相同,故可将膜孔灌三维入渗简化为二维入渗问题:由剖面(过膜孔中心的垂直剖面)上方的膜孔水室对剖面进行入渗的二维入渗问题,该膜孔水室为从−到(为膜孔半径)、单位宽度的线状水室,在此将线状水室看作压力水头为(为膜孔水室水头)的线状入渗源。

注:d为膜孔半径,cm;H′为膜孔水室水头,cm。

注:L为点(x,0)到点(a,b)的渗流路径,即2点间距离,cm。
1.2.2 膜孔灌Green-Ampt入渗模型
1)基本假设
在一维Green-Ampt入渗公式中,假设湿润锋面为水平湿润锋,即从有薄层积水的土壤表层各点入渗到水平湿润锋面与之垂直对应的各点其水分通量相同,且土层分为湿润区(土壤含水率为饱和含水率)和为湿润区(土壤含水率为初始含水率)。参考一维Green-Ampt入渗公式假设,膜孔灌Green-Ampt入渗公式假设线状入渗源(下文中简称线源)入渗到概化湿润锋上各点的水分通量均相同;并假设湿润区土壤含水率为饱和含水率,未湿润区含水率为初始含水率。另外,在入渗开始时,膜孔水室处的表层土壤其含水率为饱和含水率。
2)模型推导
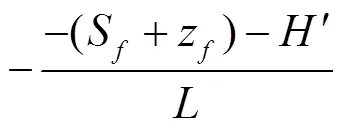
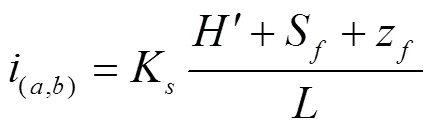
式中(a,b)为点(,0)到点(,)的入渗率,cm/min;K为表征导水率,cm/min;z为概化湿润锋上点(,)深度,cm;S为湿润锋面处水吸力,cm;为水室水头,cm;为点(,0)到点(,)的渗流路径,即2点间距离,cm。
此为线源任一点(,0)处的入渗公式。
渗流路径计算公式为
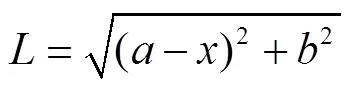
式中为渗流路径,cm。
、分别为概化湿润锋一点横、纵坐标,cm;为线源任一点横坐标值,cm。
因而其水分通量为
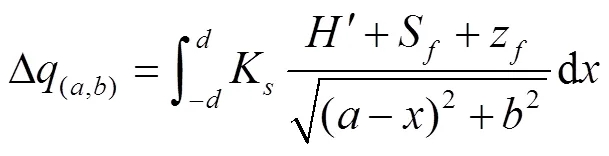
式中Δ(a,b)为线源对点(,)的水分通量,cm2/min,其中线源视为宽度为单位1,长度为2的入渗源。
式(6)的积分结果为
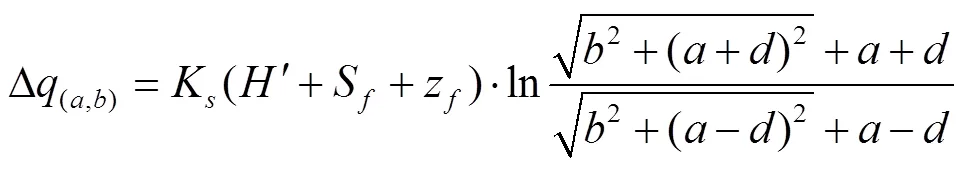
式中各符号含义同式(6)。
用概化湿润锋上任意一点(,)代替点(,),其中≥0(当=0时,>),则式(7)可化为
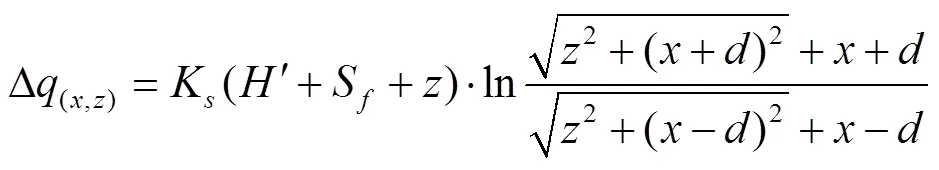
式中、为概化湿润锋任一点坐标值,cm。
此即为概化湿润锋曲线。当≤0时,积分后得到Δ(x,z)相同。
依据基本假设中概化湿润锋上各点水分通量相同,即各点处Δ(x,z)均相同,则整个湿润锋线源水分通量Δ为
D=D(x,z)(9)
依线源视为宽度为单位1,长度为2的入渗源可知,入渗率为线源水分通量与其面积的比值(这里仅取轴右半边线源面积),使用下式计算

将式(8)代入式(10)得
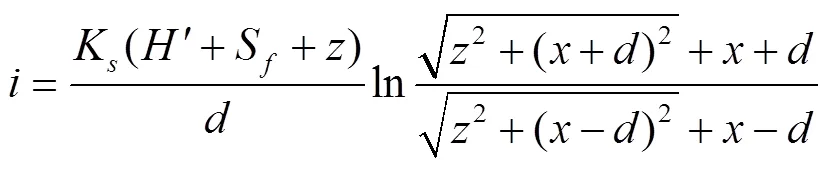
如此,当入渗率为已知的值时,即可求得关于和湿润锋的曲线(,),由此可得到湿润锋的形状。由于大田灌溉中湿润体形状不便获取,为保障灌溉水的合理应用,了解清楚膜孔灌土壤湿润体特性规律,进而选择适宜的膜孔灌技术参数对于有效调控土壤水分分布显得十分重要。
3)模型讨论
将(,)绕Z轴旋转1周,即利用式(12)进行积分即可得到湿润体的表达式为

式中为旋转体(此处为湿润体)的体积,cm3;()为绕轴旋转的连续曲线,cm;1、2为积分上下限。
因由上得到的(,)为一个关于和的隐函数,难以使(,)化为形如=()的形式,故直接利用式(14)进行积分不可行。可结合数值分析中求积分的方法复化辛普森公式计算概化湿润体体积:利用Matlab软件画出其函数图像及图像上各点的值后,再进行积分计算得到概化湿润体体积。
由水量平衡原理,可得出累积入渗量()和湿润体之间得关系
()=(−)(13)
式中()为膜孔灌累积入渗量,cm3;为时间,min;θ、θ为土壤饱和含水率和初始含水率,cm3/cm3;为概化湿润体体积,cm3。
将计算得到的值代入式(13)后只可得到一个确定的累积入渗量值,不能得到湿润锋曲线(,)和湿润体体积随时间的变化关系。因此基于此方法难以直接建立类似于一维垂直入渗中Green-Ampt公式中湿润锋随时间的变化关系。
综上,本文建立了湿润锋形状与入渗率之间的关系,而对于Green-Ampt公式中湿润锋形状随时间变化的模型仍需进一步探索。
2 试验及模拟方法
验证中采用复化辛普森公式计算概化湿润锋面积。为评价1.2节中模型的准确性,进行膜孔灌室内试验和Hydrus-2D软件膜孔灌数值模拟,主要通过单位面积累积入渗量和湿润锋运移过程来验证,并利用均方根误差、偏差百分比和平均绝对误差来评价模型计算结果的准确性。
2.1 膜孔灌室内试验
2.1.1 试验装置
膜孔灌试验装置如图4所示共分为马氏瓶、膜孔和土箱3个部分。土箱规格为24 cm×20 cm×30 cm大小,使用厚度为10 mm的有机玻璃制成。为方便观察湿润锋,使用了1/4膜孔,膜孔使用5 mm厚的有机玻璃制成,水室高4 cm,试验时将膜孔置于土箱一角,并使用马氏瓶为试验供水。
2.1.2 试验方法
供试土样为西安粉砂土,风干碾碎后过2 mm筛,以备后用。土壤颗粒由英国生产的Mastersizer-2000激光粒度分析仪(英国马尔文仪器有限责任公司)测定,粒径在≤0.002,>0.002~0.02,>0.02~2 mm的体积分数分别为9.79%,56.61%,33.60%;土壤水分特征曲线采用van Genuchten模型,其参数通过RETC软件获得。土壤饱和导水率为0.025 cm/min、经验拟合参数和分别为0.137和1.16、经验拟合参数为0.006 cm-1、饱和含水率0.479 cm3/cm3、滞留含水率0.048 cm3/cm3。
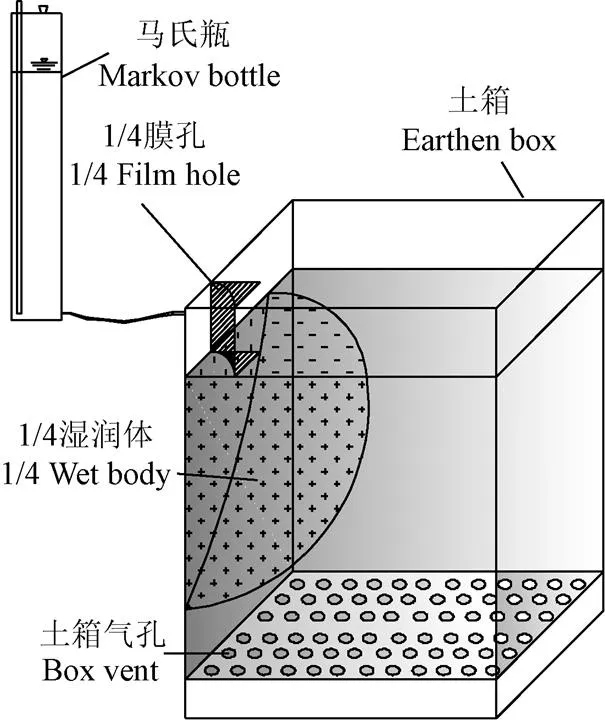
图4 试验装置图
试验中土壤容重设置为1.30 g/cm3。装填土箱时,每5 cm按设置容重计算后进行压实装填,层间打毛。为验证膜孔灌Green-Ampt入渗模型,本次试验以膜孔直径作为影响因素,设置3个不同的处理,各处理膜孔直径分别为4、6和8 cm,每个处理重复3次。
试验观测内容包括:1)试验持续5 h,入渗开始后按先密后疏的时间间隔(1、3、5、10、20、30、40、50、60 min,以后每隔30 min记录一次)记录马氏瓶读数,用以计算累积入渗量;2)在土箱外壁上描绘不同时刻的湿润锋的位置及形状。
2.2 膜孔灌数值模拟
2.2.1 模拟土壤特性
数值模拟使用Hydrus-2D软件对不同膜孔直径的膜孔灌进行模拟。为保证土壤的广泛性和研究成果的普适性,采用了Hydrus-2D软件中的3种典型土质(典型砂壤土、典型壤土和典型粉壤土)进行模拟,其基本物理参数如表1所示。数值模拟中采用6 cm的膜孔直径,水头为4 cm。

表1 典型土壤物理参数
2.2.2 膜孔灌数学模型
膜孔灌入渗为三维充分供水条件下的入渗,由于单点源自由入渗在平面上轴对称,因此将膜孔灌简化为如图5所示的二维问题进行研究。图5为膜孔灌自由入渗纵向剖面图。
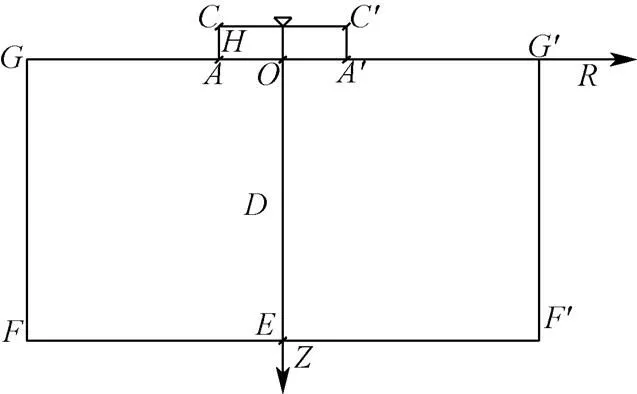
图5 膜孔灌自由入渗剖面图
1)膜孔灌自由入渗土壤水分运动基本方程
假设土壤为均质、各向同性、骨架不变形的多孔介质,不考虑率温度和源汇项的影响,则土壤水分运动方程为
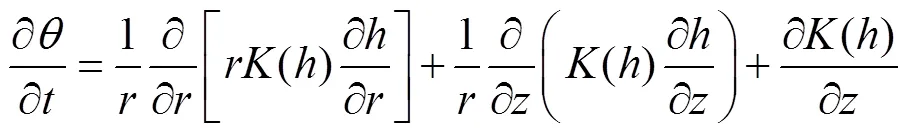
式中为土壤体积含水率,cm3/cm3;为径向坐标,cm,规定向右为正;为垂向坐标,cm,规定向下为正;为入渗时间,min;为土壤负压水头,cm;()为非饱和土壤导水率,cm/min。
2)初始条件
土壤初始含水率分布均匀时,土壤水分运动的初始条件为
(,)=0≤≤;0≤≤;=0 (15)
式中θ为土壤的初始含水率,cm3/cm3;为模拟区域边界在径向的坐标,cm;为模拟区域边界在垂直方向的坐标,cm。
3)边界条件
上边界
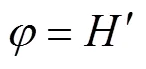
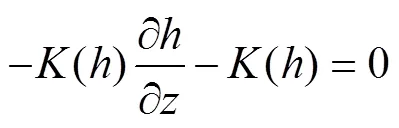
下边界
=0≤≤;=;>0 (18)
左边界
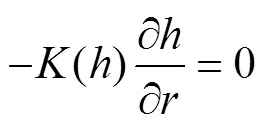
右边界
==;0≤≤;>0 (20)
式中为膜孔水室水头,cm;为模拟区域边界在径向的坐标,cm;为模拟区域边界在垂直方向的坐标,cm。
2.3 统计分析
为评价模型准确性,利用统计学中均方根误差(root mean square error,RMSE)、偏差百分比(percentage of bias,PBIAS)和平均绝对误差(mean absolute error,MAE)3个指标,对模型中公式计算值与试验观测值和数值模拟值之间的符合度进行评价分析。各指标定义如下
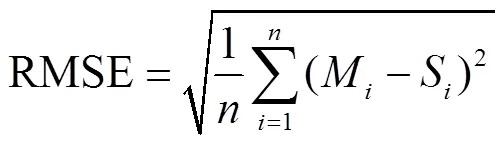
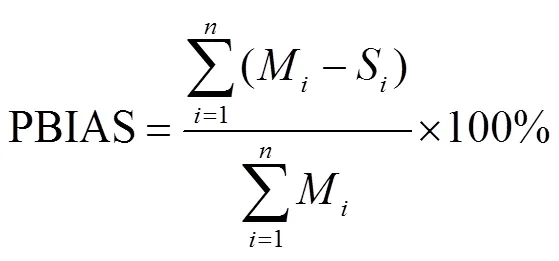
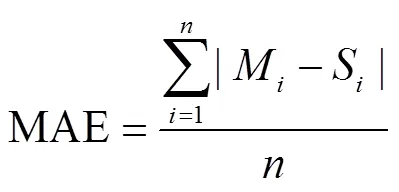
式中RMSE为均方根误差;PBIAS为偏差百分比;MAE为平均绝对误差;M为第个观测值或模拟值;S为第个计算值;为数据总个数。
RMSE和MAE越接近0,PBIAS<±10%时,表示计算值与试验观测值和数值模拟值差异越小,两者吻合越好。
3 结果与分析
3.1 累积入渗量计算结果验证
使用1.2节中推导得到的式(11)、式(12)和式(13)计算得到单位膜孔面积累积入渗量与试验观测值和数值模拟值进行比较,以验证推导得到的膜孔灌三维Green-Ampt入渗模型的准确性。试验和数值模拟土壤参数及其他条件在第2节中详细给出。
单位膜孔面积累积入渗量模型公式计算值与观测值和模拟值之间的比较如图6所示。

a. 试验观测值与计算值
a. Experimental and calculated values
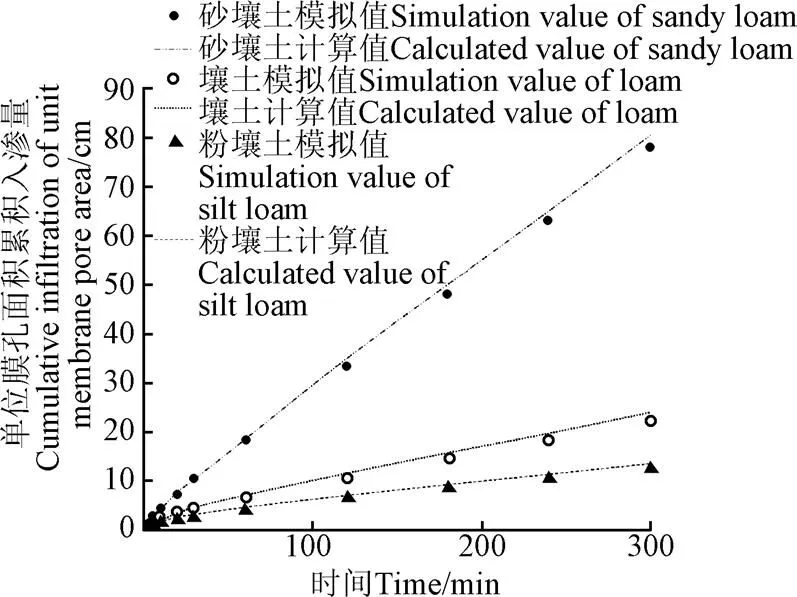
b. 数值模拟值与计算值
从图6中可以得出:1)单位膜孔面积累积入渗量的计算值与观测值和模拟值的RMSE分别为0.96和0.76 cm,RMSE接近于0;PBIAS分别为−4.8%和−3.1%,PBIAS<10%;MAE分别为0.54和0.11 cm,MAE接近于0;3组统计学指标均符合要求,计算值大小接近于观测值和模拟值。计算值和观测值以及模拟值随时间变化规律相一致,计算值整体略大于观测值以及模拟值,其入渗前期的大小差别小于入渗后期;2)试验观测值中不同膜孔直径的处理观测值与计算值接近程度不同,各处理均方根误差从大到小为1.14(6 cm)>0.93(8 cm)>0.82(10 cm),膜孔直径为6 cm的处理其观测值与其计算值偏离程度大于其他2个处理,这可能是由于试验过程中膜孔直径越小时,试验观测值的相对误差将越大;3)通过对比数值模拟值与计算值可发现,典型粉壤土的模拟结果与其计算值吻合程度最高,这是因为模型基本假设中将土壤分为湿润区和未湿润区,而粉壤土实际入渗情况中含水率的分布更加接近此基本假设[19]。
3.2 湿润锋计算结果验证
依据1.2节中式(13)计算得出概化湿润锋与试验及模拟所得湿润锋进行比较,因篇幅有限,仅列出试验中直径为6 cm湿润锋观测值及典型壤土模拟值与模型公式计算值的对比情况,如图7所示。

a. 试验观测值与计算值
a. Experimental and calculated values
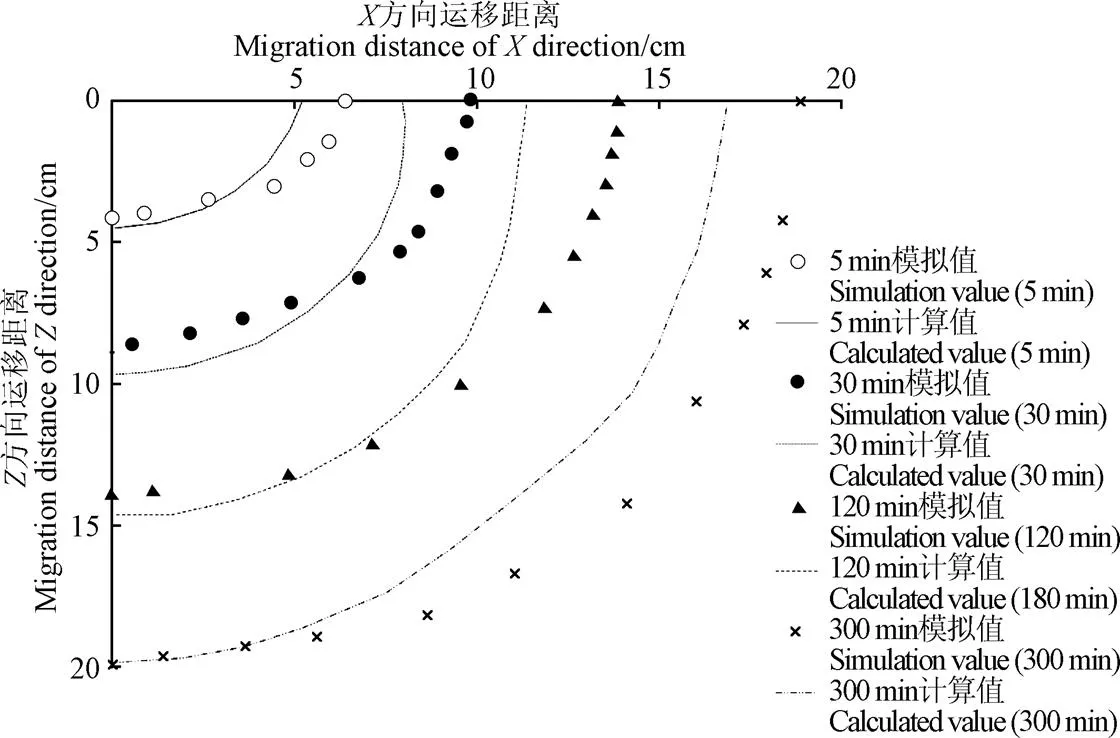
b. 数值模拟值与计算值
由图7可知,1)概化湿润锋计算值与湿润锋观测值及模拟值随时间变化规律一致,形状均类似1/4椭圆[22],试验观测和数值模拟的湿润锋范围整体上均大于计算得到的概化湿润锋值,这是因为实际入渗中,湿润锋范围内的土壤含水率存在饱和区、过渡区[23],在过渡区含水率未达到饱和状况,而在概化湿润锋范围内含水率为饱和含水率,故试验和模拟得到的湿润锋范围大于计算得到的概化湿润锋范围;2)与方向相比较,方向上计算得到的概化湿润锋与湿润锋观测值和模拟值差值更小,计算结果更吻合。依据文献[24],水分运移过程中,在垂直方向上同时受到压力水头、基质势和重力势的作用,而在水平方向上仅有基质势作用,所以水平方向的湿润锋水分运移较慢,含水率变化较大,因此1.2节中膜孔灌三维Green-Ampt公式计算得到的概化湿润锋在方向(垂直方向)比方向(水平方向)更加接近实际湿润锋。
4 结 论
基于一维Green-Ampt入渗公式,建立了膜孔灌条件下的三维Green-Ampt入渗模型。为验证推导所得模型的准确性,利用膜孔灌室内试验和数值模拟试验对其进行验证,得出如下结论:
1)比较了单位膜孔面积累积入渗量模型公式计算值与试验观测值和数值模拟值,统计分析指标均方根误差和平均绝对误差接近于0,偏差百分比<10%,建立的模型的可靠性得到了验证。计算值和观测值以及模拟值随时间变化规律相一致,计算值整体略大于观测值以及模拟值。
2)膜孔直径为6 cm的处理较膜孔直径为8和10 cm处理其累积入渗量计算值相对观测值差异更大;
3)相较于典型砂壤土和典型壤土,典型粉壤土的累积入渗量计算值与模拟值吻合程度更高;
4)概化湿润锋计算值与湿润锋观测值和模拟值随时间变化规律一致,试验观测和数值模拟的湿润锋范围整体上均大于计算得到的概化湿润锋值。方向上计算得到的概化湿润锋比方向计算结果更吻合。
[1] Green W H, Ampt G A. Studies in soil physics. I. The flow of air and water through soils[J]. J Agr Sci, 1911, 4: 1-24.
[2] Hammecker C, Antonino A C D, Maeght J L, et al. Experimental and numerical study of water flow in soil under irrigation in northern Senegal: Evidence of air entrapment[J]. European Journal of Soil Science, 2010, 54(3): 491-503.
[3] Paulus R, Dewals B J, Erpicum S, et al. Innovative modelling of 3D unsaturated flow in porous media by coupling independent models for vertical and lateral flows[J]. Journal of Computational and Applied Mathematics, 2013, 246(5): 38-51.
[4] 梁嘉平,史文娟,王全九.添加-聚谷氨酸条件下Philip模型与Green-Ampt入渗模型的对比分析[J]. 干旱地区农业研究,2017,35(3):74-79.
Liang Jiaping, Shi Wenjuan, Wang Quanjiu. Comparison analysis of Philip model and Green-Ampt infiltration model under condition of added-PGA[J]. Agricultural Research in the Arid Areas, 2017, 35(3): 74-79. (in Chinese with English abstract)
[5] 周蓓蓓,侯亚玲,王全九.枯草芽孢杆菌改良盐碱土过程中水盐运移特征[J]. 农业工程学报,2018,34(6):104-110.
Zhou Beibei, Hou Yaling, Wang Quanjiu. Characteristics of water and salt migration in process of improving saline alkali soil with bacillus subtilis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(6): 104-110. (in Chinese with English abstract)
[6] Bouwer H. Infiltration of water into nonuniform soil[J]. Peoc ASCE, 1969, 95(IR4): 451-462.
[7] 张光辉,邵明安.用土壤物理特性推求Green-Ampt入渗模型中吸力参数Sf[J]. 土壤学报,2000,37(4):553-557.
Zhang Guanghui, Shao Ming'an. Using soil physical propertles to determine the absorptire parameter Sf in green-ampt infiltration model[J]. ACTA Pedologica Sinica, 2000, 37(4): 553-557. (in Chinese with English abstract)
[8] 马娟娟,孙西欢,郭向红.基于Green-Ampt模型的变水头积水入渗模型建立及其参数求解[J]. 水利学报,2010,41(1):61-67.
Ma Juanjuan, Sun Xihuan, Guo Xianghong. Varying head infiltration model based on Green-Ampt model and solution to its key parameters[J]. Journal of Hydraulic Engineering, 2010, 41(1): 61-67. (in Chinese with English abstract)
[9] 王全九,邵明安,汪志荣,等.Green-Ampt公式在层状土入渗模拟计算中的应用[J]. 土壤侵蚀与水土保持学报,1999,5(4):66-70.
Wang Quanjiu, Shao Ming'an, Wang Zhirong, et al. Application of green-ampt equation during infiltration in layered soil[J]. Journal of Soil Erosion and Soil and Water Conservation, 1999, 5(4): 66-70. (in Chinese with English abstract)
[10] Hu H Y, Jin J, Cheng D J, et al. Influence of plant space on dynamic changes of soil nitric nitrogen sunder film hole irrigation[J]. Procedia Engineering, 2012, 28: 246-251.
[11] 徐首先,魏玉强,聂新山,等.膜孔灌理论及实用技术初步研究[J]. 水土保持研究,1996,3(3):23-29.
Xu Shouxian, Wei Yujiang, Nie Xinshan, et al. Theory of film holer irigation and practieal technology research[J]. Research of Soil and Water Conservation, 1996, 3(3): 23-29. (in Chinese with English abstract)
[12] 刘利华,费良军,陈琳,等.膜孔直径对浑水膜孔灌土壤水氮运移特性的影响[J]. 水土保持学报,2018,32(3):126-131.
Liu Lihua, Fei Liangjun, Chen Lin, et al. Effect of film hole diameter on transport characteristics of water and nitrogen in soil under film hole irrigation with muddy water[J]. Journal of Soil and Water Conservation, 2018, 32(3): 126-131. (in Chinese with English abstract)
[13] 陈琳,费良军,刘利华,等.土壤初始含水率对浑水膜孔灌肥液自由入渗水氮运移特性影响[J]. 水土保持学报,2018,32(2):58-66.
Chen Lin, Fei Liangjun, Liu Lihua, et al. Effects of soil initial water content on transport characteristics of free infiltration water and nitrogen under film hole irrigation with muddy water[J]. Journal of Soil and Water Conservation, 2018, 32(2): 58-66. (in Chinese with English abstract)
[14] 董玉云,费良军,贾丽华.灌溉定额对膜孔灌玉米土壤水氮分布和产量的影响[J]. 土壤通报,2014,45(5):1083-1088.
Dong Yuyun, Fei Liangjun, Jia Lihua. Effects of different irrigation times on water and nitrogen distribution and maize yield under film hole irrigation[J]. Chinese Journal of Soil Science, 2014, 45(5): 1083-1088. (in Chinese with English abstract)
[15] 费良军,程东娟,雷雁斌,等. 膜孔灌单点源入渗特性与数学模型研究[J]. 西北农林科技大学学报:自然科学版,2007,32(5):212-216.
Fei Liangjun, Cheng Dongjuan, Lei Yanbin, et al. Study on the infiltration characteristic and the mathematical model of the point source free infiltration under film hole irrigation[J]. Journal of Northwest A& F University: Nat Sci Ed, 2007, 32(5): 212-216. (in Chinese with English abstract)
[16] 马孝义,范严伟,王术礼,等. 膜孔灌平均入渗水深简化计算模型建立与验证[J]. 农业机械学报,2009,40(8):67-73.
Ma Xiaoyi, Fan Yanwei, Wang Shuli, et al. Simplified infiltration model of film hole irrigation and its validation[J]. Transactions of the Chinese Society of Agricultural Machinery, 2009, 40(8): 67-73. (in Chinese with English abstract)
[17] 范严伟,赵彤,赵文举,等.膜孔灌灌溉入渗量的简化计算方法及验证[J]. 农业工程学报,2016,32(13):67-74.
Fan Yanwei, Zhao Tong, Zhao Wenju, et al. Simplified calculation method and its validation of infiltration capacity for film hole irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(13): 67-74. (in Chinese with English abstract)
[18] 钟韵,费良军,刘乐.膜孔灌溉下土壤入渗特征的多因素分析[J]. 水科学进展,2018,29(4):505-513.
Zhong Yun, Fei Liangjun, Liu Le, et al. Analysis on soil infiltration characteristics of film hole irrigation as affected by multi-factors[J]. Advances in Water Science, 2018, 29(4): 505-513. (in Chinese with English abstract)
[19] 雷志栋,杨诗秀,谢森传. 土壤水动力学[M]. 北京:清华大学出版社,1988:227.
[20] 范严伟,赵彤,白贵林,等. 水平微润灌湿润体HYDRUS-2D模拟及其影响因素分析[J]. 农业工程学报,2018,34(4):115-124.
Fan Yanwei, Zhao Tong, Bai Guilin, et al. HYDRUS-2D simulation of soil wetting pattern with horizontal moistube-irrigation and analysis of its influencing factors[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(4): 115-124. (in Chinese with English abstract)
[21] 缴锡云,王文焰,张建丰. 单点膜孔入渗特性的试验研究[J]. 水利学报,1999,30(7):34-40.
Jiao Xiyun, Wang Wenyan, Zhang Jianfeng. Experimental research on infiltration from single hole of membrane[J]. Journal of Hydraulic Engineering, 1999, 30(7): 34-40. (in Chinese with English abstract)
[22] 费良军,吴军虎,王文焰,等. 充分供水条件下单点膜孔入渗湿润特性研究[J]. 水土保持学报,2001,15(S1):137-140.
Fei Liangjun, Wu Junhu, Wang Wenyan, et al. Study on wetting characteristics of point source infiltration under film hole irrigation[J]. Journal of Soil and Water Conservation, 2001, 15(S1): 137-140. (in Chinese with English abstract)
[23] 彭振阳,黄介生,伍靖伟,等. 基于分层假设的Green-Ampt模型改进[J]. 水科学进展,2012,23(1):59-66.
Peng Zhenyang, Huang Jiesheng, Wu Jingwei, et al. Modification of Green-Ampt model based on the stratification hypothesis[J]. Advances in Water Science, 2012, 23(1): 59-66. (in Chinese with English abstract)
[24] 陈琳,费良军,刘利华,等. 土壤初始含水率对浑水膜孔灌肥液自由入渗水氮运移特性影响[J]. 水土保持学报,2018,29(2):58-66.
Chen Lin, Fei Liangjun, Liu Lihua, et al. Effects of soil initial water content on transport characterics of free infiltration water and nitrogen under film hole irrigation with muddy water[J]. Journal of Soil and Water Conservation, 2018, 29(2): 58-66. (in Chinese with English abstract)
Development and verification of 3D Green-Ampt based membrane pore infiltration model
Fei Liangjun, Kang Shouxuan, Nie Weibo, Zhong Yun, Jiang Ruirui, Chen Lin
(State Key Laboratory Base of Eco-hydraulic Engineering in Arid Area, Xi'an University of Technology, Xi'an 710048, China)
Film hole irrigation is an advanced low-cost and high-efficiency irrigation method, which can improve water conservation and water use efficiency. The study presented a three-dimensional infiltration model of film hole based on the one-dimensional Green-Ampt infiltration model and further explored the hypothesis that the generalized wetting front was flat in the one-dimensional formula. Given the characteristics of 3D infiltration of membrane pore irrigation, we discussed the shape of infiltration source, and proposed a line source of infiltration source. And the study presented hypothesis that water flowed from liner score of infiltration source to every point at wetting front. Based on the hypothesis, a three-dimensional Green-Ampt model for membrane pore irrigation including film hole diameter, characteristics of water conductivity and wetting front suction was established. Moreover, the model proposed in this study was validated and evaluated by laboratory experimental data of film hole diameter and Hydrus-2D model based on the theory for water movement in non-saturated soil. In the laboratory experiments, diameter were used to was designed with different levels of 4, 6, and 8 cm and the experiments carried out in Sated Key Laboratory Base of Eco-hydraulics in Northwest Arid Region. The infiltration was measured by difference of water level in Markov bottle. The water level was recorded every 1, 3, 5, 10, 20, 30, 40, 50, 60 min. Wetting front were recorded on soil box surface when water levels recorded. The experiment lasted for 5 h. Each treatment of laboratory experiment was replicated 3 times. In the case of different soil textures (sandy loam soil, loam soil and silty loam soil), the dynamic change of cumulative infiltration and wetting front was simulated by Hydrus-2D. The statistical comparisons (root mean square error-RMSE, percentage of bias-PBIAS, mean absolute error-MAE) of the estimated data with the measured and simulated data were conducted. The results showed that the variation of cumulative infiltration per unit film hole area with time obtained by the measured and simulated was consistent with the cumulative infiltration per unit film hole area of the proposed model. According to comparisons of the estimated values with the measured values, the root mean square error, mean absolute error, and percentage of bias were 0.96 cm, 0.54 cm and -4.8%, respectively. The root mean square error of measured and estimated values were 1.14 (6 cm) >0.93 (8 cm) >0.82 (10 cm). Besides, the simulated cumulative infiltration value of typical silt loam was more closer to the estimated values than typical sandy loam and typical loam. Comparing estimated wetting front with the measured and simulated ones, the difference was small in initial infiltration time and gradually increased with the increase of infiltration time. In addition, compared with the horizontal direction, the estimated generalized wetting front in the vertical direction was more closer to the measured and simulated value. In summary, the established 3-D infiltration model for film hole irrigation can be used to accurately calculate the cumulative infiltration of film hole and predicte the shape of wetting front.
numerical analysis; infiltration; soils; membrane hole irrigation; Green-Ampt model; wetting front’
费良军,康守旋,聂卫波,钟 韵,姜瑞瑞,陈 琳. 基于Green-Ampt的膜孔灌三维入渗模型建立与验证[J]. 农业工程学报,2019,35(20):69-75.doi:10.11975/j.issn.1002-6819.2019.20.009 http://www.tcsae.org
Fei Liangjun, Kang Shouxuan, Nie Weibo, Zhong Yun, Jiang Ruirui, Chen Lin. Development and verification of 3D Green-Ampt based membrane pore infiltration model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(20): 69-75. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.20.009 http://www.tcsae.org
2019-03-08
2019-09-10
国家自然科学基金资助项目(51479161、51779205);国家农业公益项目(201203003-1)
费良军,教授,博士生导师,主要从事节水灌溉与农业水资源利用研究。Email:feiliangjun2008@163.com
10.11975/j.issn.1002-6819.2019.20.009
S274.3
A
1002-6819(2019)-20-0069-07

