基于单孔波形叠加的微差爆破降振研究

张家铭 程贵海 蒙国敏 王毅 王平 邓春海

摘要：为了确定在某水电站在开挖爆破中电子雷管延期时间，实现最好的降震效果，采用了单孔爆破震动波形叠加的方法。将首爆炮孔与后续起爆炮孔之间的孔间延时设置为1s，并且进行爆破振动监测。通过MATLAB软件读取单孔振动波形，并根据130个炮孔的单孔药量对振动波形加权叠加，又将5组单孔波形分别以微差时间1-200ms进行叠加。结果表明：不同监测点的单孔爆破振动时长与频率均不相同;考虑到药量因素的单孔波形加权叠加具有很好的仿真效果。通过综合分析2处监测点在不同孔间延时下的振动峰值变化曲线，发现当本次爆破孔间延时为53ms时，能够实现最好的降振效果。距离爆破区域最近的两处监测点的降震率分别为78.6%、79.7%。这对于爆破施工具有很高的参考价值。

Abstract： In order to determine the delay time of the electric detonator in the excavation blasting of a hydropower station and achieve the best effect of vibration reduction， the method of superposition of vibration waveform of single hole blasting is adopted. Set the delay between the first blasting hole and the subsequent blasting hole to 1 second， and monitor the blasting vibration. The vibration wave form of single hole is read by MATLAB software， and the vibration wave form is weighted and superposed according to the single hole charge of 130 holes. Five groups of single hole waveforms are superposed with differential time of 1-200ms. The results show that the vibration duration and frequency of single hole blasting at different monitoring points are different， and the weighted superposition of single hole waveform considering the charge factor has a good simulation effect. Through the comprehensive analysis of the vibration peak change curve of two monitoring points under different delay between holes， it is found that when the delay between holes is 53ms， the best vibration reduction effect can be achieved. The seismic reduction rates of the two monitoring points close to the blasting area are 78.6% and 79.7% respectively. It has a high reference value for blasting construction.

關键词：波形叠加;降振率;孔间延时

Key words： waveform superposition;vibration reduction rate;inter hole delay

中图分类号：TU751.9                                    文献标识码：A                                  文章编号：1006-4311（2019）34-0253-05

0  引言

爆破作业是土石方开挖中的工序之一。为保证开挖效率以及效果，往往需要较多的单孔药量。然而部分爆破区域环境复杂，周边民方等建（构）筑物与爆区距离较近，因此保护爆破区域周边建筑与保证爆破开挖进度之间存在一定的矛盾。而爆破微差技术能够解决这一问题，该技术通过设定孔间延时，使各个炮孔产生的振动波形相互叠加。合理微差时间能够使各药包产生的地震波相互干涉，起到振动降低的效果。

自数码电子雷管应用以来，微差延时的精度大大提高，可精确至1ms以内。这使微差延时爆破技术的可行性增强。不少国内外学者也对合理微差延时的设定问题进行了研究。对于爆破振动速度峰值与孔间延时的相关性，周梓彬[1]、王军跃[2]等人利用MATLAB软件的信号读取与处理功能，将单孔波形进行叠加，研究不同微差间隔下的叠加信号振速峰值;Fish.B（美）指出，采用微差起爆技术可减少爆破振动对周围建（构）筑物的影响，通过分析单孔波形明确其半周期的时间并以此作为微差延时，能够使群孔爆破振动峰值小于单孔振动峰值。建议微差延时为8～25ms[3]。

随着人们对爆破振动机理认识的加强，许多爆破行业的学者开始以多因素作为爆破安全判据，对爆破振动波形进行分析。刘小乐采用HHT法对波形进行分析，展现了非平稳信号在频域、能量方面的变化特征[4];李瑞涛分别采用小波分析法与HHT法，对不同微差爆破波形进行分析，得到HHT分析法具有更好的适应性的结论[5]。

然而上述研究在波形叠加过程中仅仅利用首爆炮孔进行叠加，未考虑在单孔药量不同时的处理方法。本文采用波形叠加原理，利用MATLAB软件将单孔爆破振动波形以不同时间间隔进行加权叠加，研究其振动速度峰值的变化规律，以此确定最佳孔间延时，达到最好的降振效果。

1  单孔叠加仿真预测法

单孔叠加仿真预测法是与传统的回归分析预测法完全不同的振动波形预测手段。该方法不需要大量监测数据进行统计分析，而是首先進行单孔爆破试验，并用测振仪监测获得单孔爆破振动信号。利用软件对振动信号进行读取和叠加计算，实现群孔波形的复现。该方法包括了地形地质条件、临空面以及爆源炸药等各方面条件，因此仿真程度较高。振动波形叠加方程可表示如下：

2  单孔振动波形的获取

2.1 炮孔起爆振动试验设计

单孔爆破振动试验在柳州某水电站的开挖爆破项目中进行。岩体主要为硬岩质中风化灰岩组成，微晶结构，厚层状、块状构造为主，岩质坚硬。本次爆破采用逐孔起爆，爆破参数由表1所示。

为获取单孔波形且不影响正常爆破施工，将本次爆破的首爆炮孔与群爆炮孔之间的时间延迟设为1s，其他孔间延时均为80ms。选取首爆炮孔作为试验点，检测到的振动波形不会受到其他爆破振动的干扰，能够获得更准确的波形原函数。单孔起爆点位于爆破区域最西侧，炮孔分布图如1所示。

2.2 爆破振动监测点布置

测试设备使用成都中科测控公司（中国科学院成都分院）生产的TC-4850新型爆破测振仪，本次测试爆破振动时所设定仪器信号触发值均为0.04cm/s。测点共有五个，形成一条侧线。最近测点与首爆孔距离20m，由于仪器与爆区距离较近，使用木板对仪隔离防护，如图2所示。其他测点之间按照等对数间隔选取，与单孔试验点距离分别为138m、234m、431m、707m。监测点位置如图3所示。

通过统计监测点的相应数据，得到了各爆破区域与监测点的距离、单段药量、振动主频以及监测点爆破振动峰值速度如表2所示。

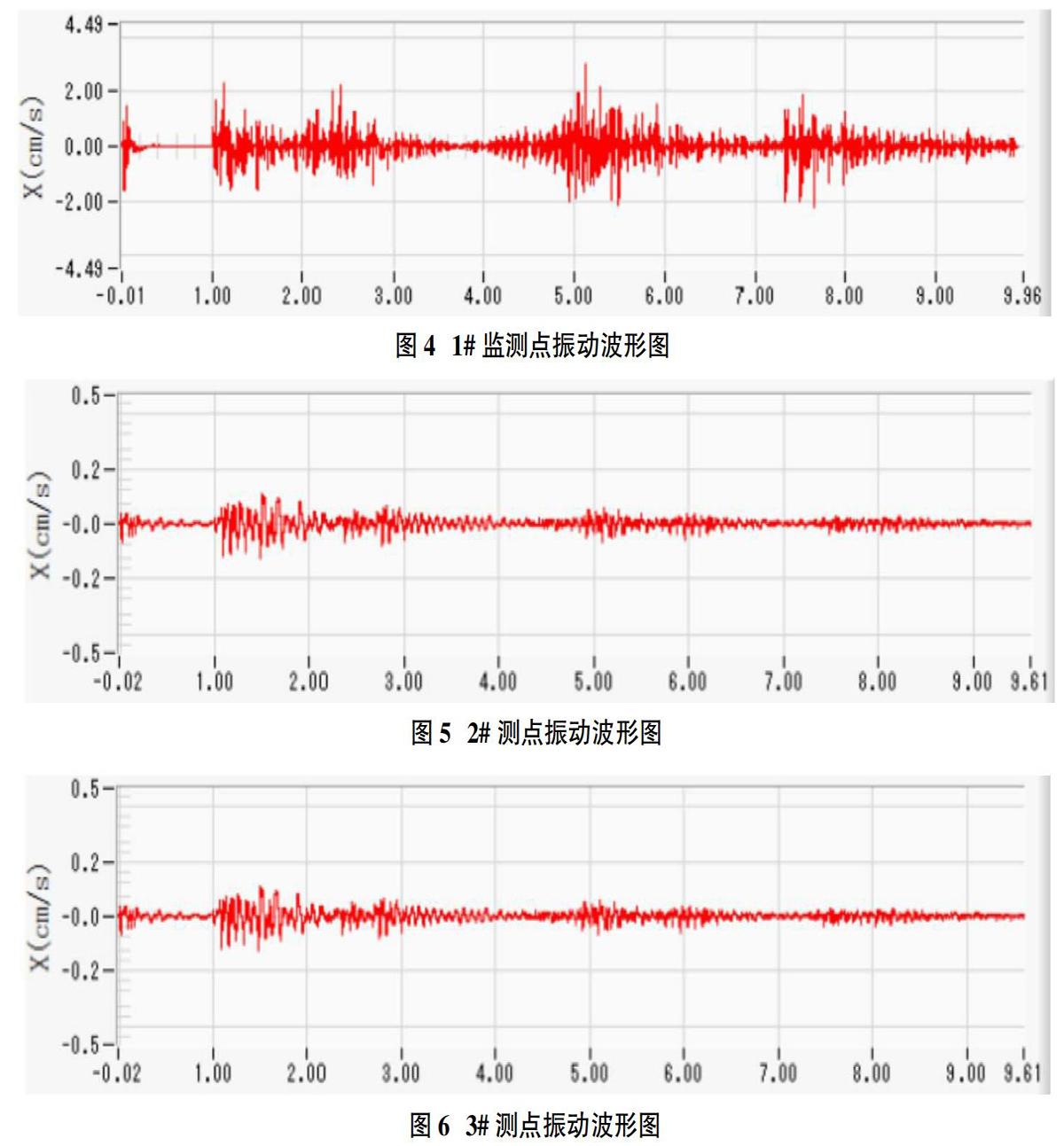
为保证监测得到的振动波形能够良好反应地质条件，采用最小二乘法对五个监测点进行线性回归，选取相关系数大于0.9的测点。通过计算与比对，证明1#、2#、3#测点具有可信度与实用价值。3个点的爆破振动波形如图4、图5、图6所示。

图4-图6充分体现了数码电子雷管的精确性。通过观察在仪器中导出的text文档数据，亦可发现爆破振动在1s处显著增强，爆破振动叠加的可行性也得到了充分的证明。

3  爆破振动波形叠加在MATLAB中的实现

3.1 单孔波形分析

为了将单孔波形从原振动谱中分离出来，从而完成叠加和分析的工作，采用MATLAB中的textread功能，选取text文档中的单孔波形振动数据，导入该软件。横轴单位为ms，纵轴单位为m/s。单孔波形如图7、图8、图9所示。

通过MATLAB编程，可输出单孔波形振动峰值。1#监测点振动峰值为1.48cm/s。2#测点振动峰值为0.10cm/s。3#测点振动峰值为-0.06cm/s。

3.2 单孔波形叠加

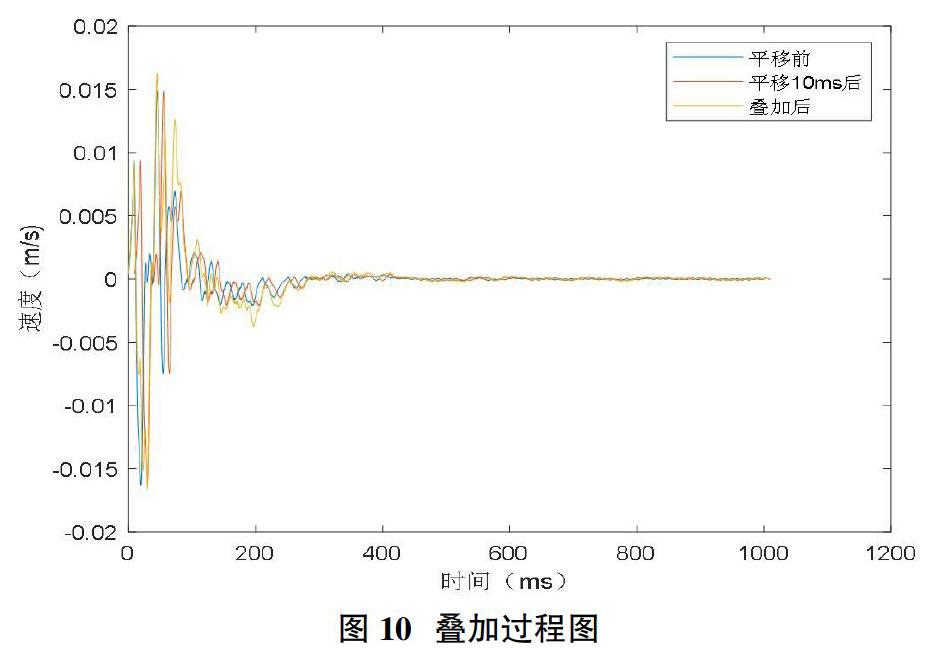
利用MATLAB的for循环算法，可将单孔波形以不同时差进行叠加。由于该单孔波形是由8001个离散的点构成，因此叠加的前提条件是采样周期为孔间微差的整数倍。通过text文档可知，测振仪每隔0.125ms即可监测一组振动数据，即使孔间延时为1ms，依然能够保证叠加正常进行。以孔间微差10ms为例，叠加过程图如图10所示。

由图可知，药量相同的两个炮孔在孔间微差为10ms的情况下，爆破振动增强。而在本项目中，共有130个炮孔，且每个炮孔药量不一致。为解决以上两个问题，可对振幅系数进行调整，即

其中，Qi为第i个炮孔的药量，ai为第i个炮孔爆破振动幅值系数。Q0为第一个炮孔的药量，a0为首爆炮孔振幅系数，可令a0=1。根据不同的单孔药量，可计算出各个炮孔在对应监测点的模拟振动数据，周期相同，频率相同而幅值不同。以微差时间叠加即可得到爆破振动预测波形。这种运算过程与卷积（convolution）的物理意义完全一致，即是响应单位（源波形）与输入信号（振幅系数）的加权叠加。由于孔数较多，逐一计算的工作量较大。而在MATLAB中可采用函数conv（p1，p2）来实现。导入单孔离散波形以及单孔药量比例系数，以固定相位差进行叠加即可获得群孔爆破模拟波形。以测点2所获取的单孔波形为例，依照实际爆破时孔间微差80ms，叠加产生的群孔爆破波形如图11所示。

通过图11与图5的对比不难发现，预测波形与实测波形的振动速度随时间变化基本相同，验证了单孔叠加仿真的精准性与全面性，在振动速度以及振动趋势上均有良好的预测效果，也证明了采用该方法获取孔间最佳微差时间的可行性很高。

3.3 合理微差时间的选择

为研究爆孔间微差时间与爆破振动峰值之间的关系，选择监测点1中五组单孔波形分别以25ms，50ms和100ms进行叠加。

由图12-图14可知，爆破孔间延时25ms时，振动峰值为1.827cm/s;振动峰值为50ms时，振动峰值为1.633cm/s;孔间延时100ms时，振动峰值为1.800cm/s。由此可知，爆破振动峰值随孔间延时的改变有一定变化。因此，为确定最佳微差时间，将孔间微差时间从1ms增至200ms，将1号、2号测点单孔波形叠加得到对应微差时间的振动波形。选取200个波形中每个波形振动速度绝对值的峰值，与对应的孔间微差时间构成振动峰值变化图像如图15、图16所示。

根据图15可知，1号监测点的振动速度峰值在孔间微差0-10ms范围内急剧下降，而后产生一定波动。孔间延时44ms时，对应的爆破振动峰值为首个极小值。而后振动的峰值基本稳定。其中，44-53ms、77-86ms、109-114ms振动峰值均为1.633cm/s，并且是定义域范围内的最小值。2号测点振动速度峰值的变化趋势与1号类似，但最小值位于孔间延时26ms处，ymax为0.102cm/s。此外在微差延时处于101-105ms时，ymax均为0.103cm/s。为更好研究微差爆破振动的降振效果，采用微差爆破降振公式進行计算。降震率可表示为：

其中， δ为爆破振动降震率，v0为齐发爆破的振动速度，v为微差爆破振动的速度峰值。通过计算，得到监测点1处的最大降震率为78.6%，2号监测点的最大降震率为79.7%。由此可见，微差延时的方法可以十分有效的降低爆破振动速度峰值。

针对于本次爆破，虽然两处监测点的ymax最小值所对应的微差时间不存在交叉现象，但依然能够通过微差曲线确定最佳微差时间。当微差时间为53ms时，1号监测点的振动峰值达到最小，2号监测点的振动峰值则达到极小值，为0.125cm/s。据此可以判断，在只考虑振动速度因素的条件下，本次爆破最佳微差时间为53ms。

通过观察单孔爆破在3个测振点所产生的波形，不难发现它们的振动频率以及振动时长均不相同，这是爆破振动波传播速度不同导致的。单孔炸药爆破炸后产生两种类型的波，根据传播途径划分为体波和面波。体波分为横波（S波）与纵波（P波）。面波分为勒夫波（L波）与瑞丽波（R波）。纵波速度为4-7km/s，横波速度为2-4km/s。瑞丽波的波速略小于横波速度，而勒夫波的波速与频率和波长有关[6]。最近监测点距爆破中心仅20m，各类波形几乎同时到达，而在较远距离传导过程中，波形逐渐分离。2、3号监测点距离分别为138m、234m，因此监测到的振动波形相对于1号监测点差异很大，这也导致叠加后的群孔微差爆破波形以及振动峰值变化曲线的变化趋势有所不同。由此论证，在不同监测点获取对应单孔振动波形，再进行微差时间的研究是十分必要的。因其具有振动传导至监测点所产生的各种变化与特征，可使预测更为精准。

4  结论

本文基于单孔叠加仿真预测法，利用MATLAB软件进行编程，实现了单孔振动波形的叠加。该模拟方法考虑了爆破孔数以及各个炮孔的药量，计算出本次爆破在不同孔间微差时间下各个监测点的振动速度。通过分析与比较得到以下结论：①通过单孔药量之比计算各个炮孔爆破时产生振动的振幅系数，再将其与源波形通过加权叠加的运算，能够准确地预测群孔爆破振动速度随时间的变化趋势。也证明了单孔叠加预测法的可行性与精准性。②通过比较不同监测点的单孔振动波形，发现它们在振幅、频率以及振动时长上都有很大不同。一方面验证了各类振动波形在传播速度上的差异，另一方面也说明，在进行波形叠加时，通过对应监测点的单孔波形预测群孔波形是十分必要的。③综合两处最近的监测点所获取的峰值变化曲线，可发现在孔间微差为53ms时，爆破振动的降震率最高，两处监测点的降震率分别为78.6%和79.7%。这对于该工程具有很强的指导意义。

参考文献：

[1]周梓彬.基于波形叠加的合理微差时间选取[D].东北大学，2014.

[2]王军跃.爆破振动信号叠加法及其在露天矿的应用[D].武汉理工大学，2007.

[3]Langefors，U.，Kihlstorm，B.The Modern Technique of Rock Blasting，1963.

[4]李瑞涛.爆破地震波叠加规律实验研究[D].东北大学，2008.

[5]刘小乐，袁海平，郑鑫，王占棋.基于HHT的爆破振动信号时频能量分析[J].合肥工业大学学报（自然科学版），2019，42（06）：779-784.

[6]孟吉复，惠鸿斌.爆破测试技术[M].北京：冶金工业出版社，1992.