巧解含绝对值的一元一次方程
黄晓晔
解含绝对值的方程,一个重要的基本思路就是:将含有绝对值的方程转化为不含绝对值的方程。
一、几何解法
思路:在数轴上,到一个点的距离等于一个常数的点有两个,分别在这个点的左右两侧,可利用数轴直接观察得到方程的解。
我们知道[x]的几何意义表示数轴上的数x对应的点与原点的距离,即[x]=[x-0]。这个结论可以推广为[x1-x2]表示在数轴上数x1与数x2对应的点之间的距离。
例1 已知[x]=3,求x的值。
【解析】数轴上与原点的距离为3的点对应的数分别为-3或3,即x=-3或x=3。
例2 已知[x+1]=2,求x的值。
【解析】数轴上与数-1对应的点的距离为2的点对应的数分别为-3和1,即x=-3或x=1。
例3 解方程[x-1]+[x+2]=5。
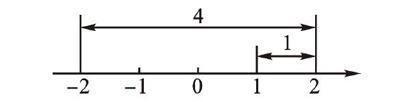
【解析】由绝对值的几何意义知,该方程表示求在数轴上与数1和数-2对应的点的距离之和为5的点对应的数,即x的值。在数轴上,数1和-2对应的点的距离为3,满足方程的x在数轴上的对应点在1的右边或-2的左边。若x对应的点在1的右边,如下图,可以看出x=2;同理,若x对应的点在-2的左邊,可得x=-3。故原方程的解是x=2或x=-3。
二、代数解法
思路:利用绝对值的性质去掉绝对值符号,把含有绝对值的一元一次方程转化成两个不含有绝对值的一元一次方程,再求解。
例4 解方程[2x-1]=5。
【解析】我们只要把2x-1看成一个整体,根据绝对值的意义进一步解决问题即可。
解:根据绝对值的意义,得2x-1=5或2x-1=-5。解这两个一元一次方程,得x=3或x=-2。
同学们可以自己检验一下。(1)当x=3时,原方程的左边=[2x-1]=[2×3-1]=5,原方程的右边=5。因为左边=右边,所以x=3是原方程的解。(2)当x=-2时,原方程的左边=[2x-1]=[2×-2-1]=5,原方程的右边=5。因为左边=右边,所以x=-2是原方程的解。
综上可知,原方程的解是x=3或x=-2。
(作者单位:江苏省常州市武进区礼嘉中学)

