循序渐进 由简到繁
江美红


勾股定理神秘而美妙,证法繁多,其中以“面积法”证明居多。国内外数学家们为了证明定理创造了很多几何图形,比较著名的图形有赵爽弦图、毕达哥拉斯图、刘徽证法图等。近几年的中考中也出现了对这类图形的考查,本文围绕几个基本图形选取一些中考题作简要讲解,希望对同学们能有所帮助。
一、赵爽弦图
例1 (2019·邵阳)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”。如图1,设勾a=6,弦c=10,则小正方形ABCD的面积是 。
【解析】题中由勾a=6,弦c=10,利用勾股定理可得股为[102-62=8],因此小正方形的边长为8-6=2,小正方形的面积为22=4,故答案是4。
【点评】本题主要考查了勾股定理,全等三角形、正方形的性质,弄清组成“赵爽弦图”各个图形之间的关系是解答本题的关键。
图1
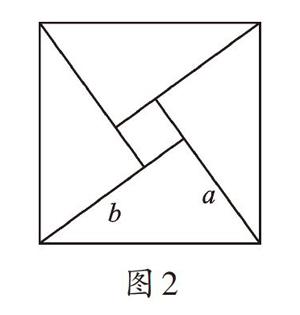
例2 (2019·大庆)我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图2所示)。如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a-b)2的值是______。
图2
【解析】由勾股定理得,a2+b2=13,直角三角形面积为(13-1)÷4=3,即[12]ab=3,得ab=6,所以(a-b)2=a2+b2-2ab=13-12=1。
【点评】本题主要考查勾股定理、完全平方公式。由题意得到关于a、b的二元二次方程组,在此不必解出a、b的值,利用整体思想求出(a-b)2即可。这里我们可以体会到整体思想的优越性。
二、毕达哥拉斯图
例3 (2019·宁波)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载。如图3,以直角三角形的各边分别向外作正方形,再把较小的两张正方形纸片按图4的方式放置在最大正方形内。若知道图中阴影部分的面积,则一定能求出()。
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
图3 图4 图5
【解析】由勾股定理可知,图3中两个小正方形面积和等于大正方形面积。设图中三个正方形边长从小到大依次为a、b、c,如图5,则S阴影=c2-a2-b2+S重叠,由勾股定理可知,c2=a2+b2,所以S阴影=S重叠,故选C。
【点评】本题利用勾股定理知识解决阴影部分的面积问题,因叠合过程中出现重叠部分,所以本题的难点是用三个正方形边长表示出图中阴影部分的面积。
三、刘徽图
例4 (2018·温州)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式。后人借助这种分割方法所得的图形证明了勾股定理。如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为()。
A.20B.24C.[994]D.[532]
图6 图7
【解析】本题欲求矩形的面积,只需求出小正方形的边长即可。如图7,设小正方形的边长为x,则AC=3+x,BC=4+x。在Rt△ABC中,利用勾股定理可建立关于x的方程(3+x)2+(4+x)2=72,整理得:x2+7x-12=0,而长方形的面积为x2+7x+12=12+12=24,∴该矩形的面积为24,故选B。
【点评】本题考查勾股定理的证明及应用、一元二次方程的应用。在融合数学文化的同时,注重整体思想和数形结合等思想方法。
以上问题的出现,是近几年中考数学卷的一大特色。它们依托数学文化,关注核心素养,体现数学的人文价值。在学习过程中,同学们要提升在新技术情境下理解知識并将这些知识迁移到不同情境中的能力。
(作者单位:江苏省太仓市实验中学)

