考虑回收质量不确定的再制造专利许可策略研究

杜茂康，王 强，李晓光

(重庆邮电大学 经济管理学院， 重庆 400065)

科技的飞速发展和人们生活水平的提高使得产品的更新频率逐渐加快，产品的使用周期也越来越短。然而，产品周期的变短使得废旧产品越来越多，这些废旧产品如果不加以处理，不仅会导致资源的浪费，还会导致环境的污染。为了解决这一问题，再制造应运而生。不仅如此，再制造在解决环境污染、避免资源浪费的同时，也带来巨大的经济效益，如美国施乐公司在1995年就制定了“垃圾零填埋”的产品循环利用政策，使得公司每年可节约资金近2亿美元[1]。

再制造产业巨大的经济效益和环保效益吸引着越来越多的企业进入该领域。而现实中，可能考虑到成本或品牌保护，很多原始制造商不愿意从事再制造[2]，这也导致越来越多的企业为了满足市场的需求专门从事再制造行业。这些第三方再制造商的出现不可避免地会对原始制造商生产的新产品带来一定的影响，为了应对再制造厂商的竞争威胁，原始制造商需要采用合理的手段去保障自己的利益，其中，再制造专利许可就是最有效的手段之一[3]，如著名的再生墨盒侵权案[4]。

目前已有很多学者对再制造专利许可进行过研究，如Muto等[5]在差异化产品的基础上研究发现，相对于固定费用专利许可，采用提成费用专利许可会更优。Faulí-Oller等[6]则进一步研究了2部制专利许可模式下闭环供应链的最优策略。熊中楷等[7]在研究专利许可下再制造闭环供应链问题的同时，使用收益共享-费用分担契约对闭环供应链系统进行了协调。郑本荣等[8]使用改进的收益共享契约对专利许可下双渠道闭环供应链系统进行了协调。易余胤等[9]比较了固定费用专利许可模式和单位费用专利许可模式下各决策变量的均衡解和最优利润。许民利等[10]在把消费者分为普通消费者和绿色消费者的基础上，发现专利许可下再制造商会更倾向高价策略，即把再制造品以高价出售给绿色消费者。Hong等[11]研究发现，当原始制造商和再制造商都参与再制造时，原始制造商采用何种专利许可策略由固定费用的门槛决定。

以上的研究都是基于废旧产品的回收质量是确定且同质的，而在现实生活中，由于人们对产品的使用习惯和使用时间的不同，即使是回收同种类型的废旧产品，其质量也是相差较大的。针对回收质量的不确定性，Guide等[12]对回收不同质量水平的废旧电话通过再制造达到同样质量水平，并以一定价格进行销售的便携式电话再制造公司进行了研究。Aksen等[13]假设回收的废旧产品存在多个质量等级，研究了政府补贴对企业废旧产品回收的影响。高雅等[14]假设回收质量水平服从指数分布且回收率等都是有关最低回收质量的函数，结果发现制造商更倾向以成本最低的方式回收质量水平较低的回收品。邓乾旺等[15]探讨了回收质量不确定下3种政策机制对闭环供应链的影响，认为政府补贴和碳税相结合的机制更有效。程发新等[16]探讨了政府差别补贴和回收质量不确定对闭环供应链定价决策的影响，研究发现提高回收质量有利于制造商和再制造商利润以及回收数量的增加。

上述文献大多数单一地研究了专利许可或回收质量不确定性对再制造闭环供应链的影响，而现实生活中，当原始制造商对再制造商进行专利许可时，产品回收过程中回收质量的不确定性是始终存在的。因此，针对市场上存在的多种再制造专利许可策略，研究回收质量不确定下制造商的再制造专利许可策略选择问题是很有必要的。本文综合运用博弈论、消费者效用理论等相关理论和方法，在专利许可与再制造闭环供应链相关理论的基础上，分别构建了单位费用专利许可策略及固定费用专利许可策略下制造商和再制造商的利润模型，并利用博弈论的相关理论方法求得不同策略下闭环供应链的均衡解。通过对不同策略之间各均衡解的比较分析以及对模型研究结果进行的数值算例分析，从不同的角度探讨了专利许可下回收质量的不确定性对再制造闭环供应链的影响，并进一步研究了在回收质量不确定下制造商的再制造专利许可策略选择问题，以期对现实中的制造企业提供指导意义。

1 相关假设与符号说明

本文考虑由一个原始制造商和一个再制造商组成的两周期闭环供应链系统，其中制造商负责生产和销售新产品，再制造商负责生产和销售再制造品。在第1周期，市场上只有新产品，第2周期，市场上会出现再制造品和新产品。为了简化研究过程，本文假设制造商与再制造商之间的信息是完备的且都是以利润最大化为目标，而且再制造商回收的旧产品可全部用于再制造。

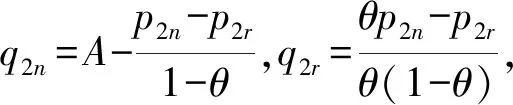
在回收质量不确定时，假设回收价格和再制造成本均与回收质量有关，其中旧产品的回收价格r=r0+δm[17]，其中r0表示回收产品的基本价格；δ表示回收质量系数；m表示回收质量，0≤m≤1。第2期再制造品的单位再制造成本，cr=ke1-φm[18]，其中k表示修复成本系数；φ表示质量成本系数。

本文中的下标i=n,r分别表示新产品、再制造商生产的再制造品，上标j=R,F分别表示单位费用专利许可及固定费用专利许可。在单位费用专利许可下，制造商对再制造的每单位产品收取费用，即制造商收取单位专利费；在固定费用专利许可下，再制造商进行再制造时向制造商支付一笔固定费用，即制造商收取固定专利费。

本文的符号说明如表1所示。

表1 符号说明

2 模型的建立与求解

第1期时，市场上只有制造商生产和销售新产品，故制造商的最大利润模型为

maxπ1m=(p1-cn)q1

(1)

将p1=A-q1代入式中，得

(2)

(3)

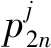
2.1 单位费用专利许可策略下模型的建立与求解

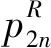
(4)

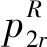
构造再制造商利润函数的拉格朗日函数为：

(5)

联立KKT条件求解可得：

(6)

(7)

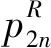
(8)

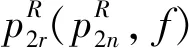
(9)

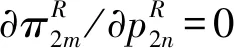
(10)

(11)

其中x0=θA-ke1-φm-r0-δm，下同；

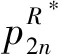
(12)

(13)

其中x1=θcn-ke1-φm-r0-δm，x2=4B+θ(1-θ)(A-cn)2，下同。

同理，将上述求得的参数代入需求函数和利润函数中可得：

(14)

(15)

(16)

(17)

2.2 固定费用专利许可策略下模型的建立与求解

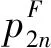
(18)

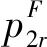
构造再制造商利润函数的拉格朗日函数为

B(τF)2-(r0+δm)τFq1-

(19)

联立KKT条件求解可得：

(20)

(21)

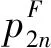
(22)

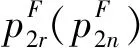
(23)

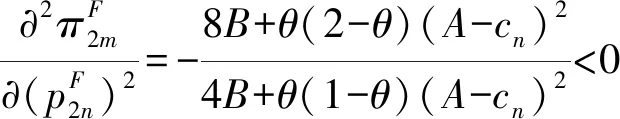
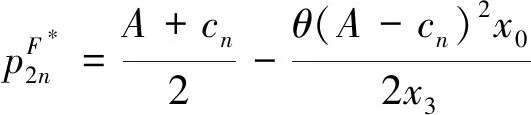
(24)

其中x3=8B+θ(2-θ)(A-cn)2，下同；

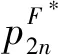
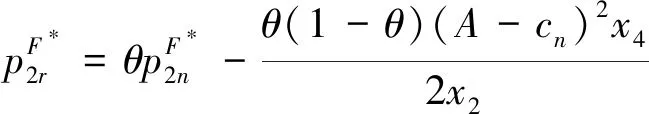
(25)

(26)

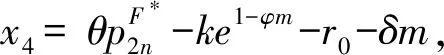
同理，将上述求得的参数代入需求函数和利润函数中可得：

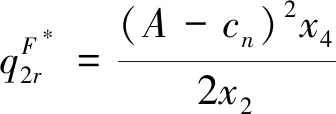
(27)

(28)

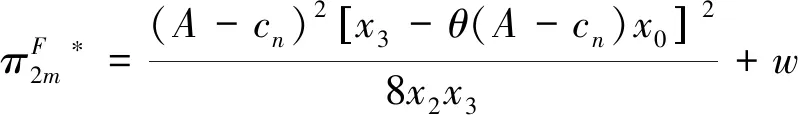
(29)

(30)

3 决策分析

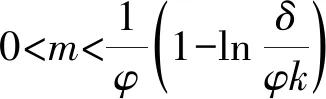
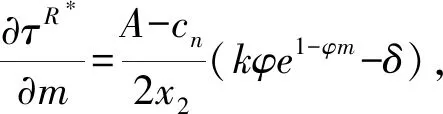
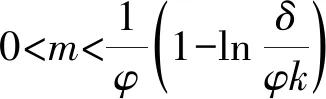
证明：证明过程同命题1。

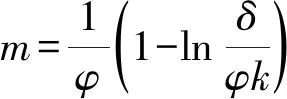
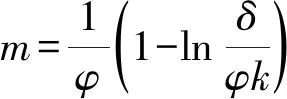
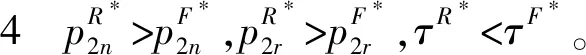
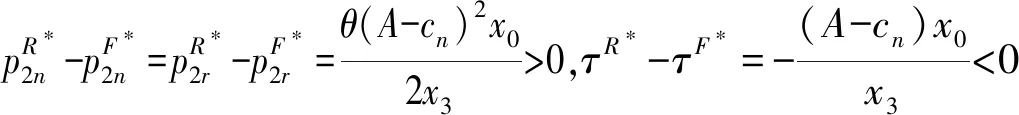
命题4表明，固定费用专利许可策略下新产品和再制造品的价格均小于单位费用专利许可策略，且固定费用专利许可策略下的回收率大于单位费用专利许可策略，所以固定费用专利许可策略对消费者和环境更有利。

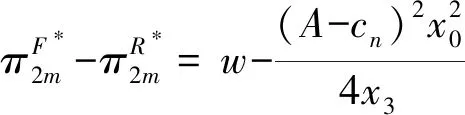
命题5表明，原始制造商选择哪种专利许可策略存在阈值，当固定专利费用大于该阈值时，制造商应选择固定费用专利许可策略；当固定专利费用小于该阈值时，制造商应选择单位费用专利许可策略。

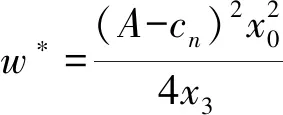
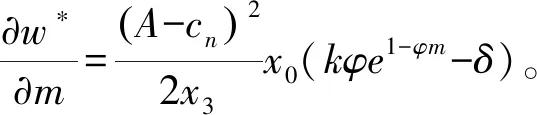
命题6表明，当再制造商的回收质量越靠近最佳回收质量，制造商的专利许可策略选择的临界值就越大，越偏向于单位费用专利许可，即制造商采取固定费用专利许可所需要的固定专利费越高。

4 算例分析

为了更好地了解回收质量m对均衡解及双方决策的影响，下面通过算例进行分析。首先令A=80，B=200，θ=0.8，cn=30，r0=5，δ=10，k=5，φ=2。

经计算，只要满足0≤m≤1，那么x0>0，x1>0，x4>0均成立，故令m在[0,1]之间变化，探讨回收质量m对均衡解及双方决策的影响，计算所得的数值如表2所示。

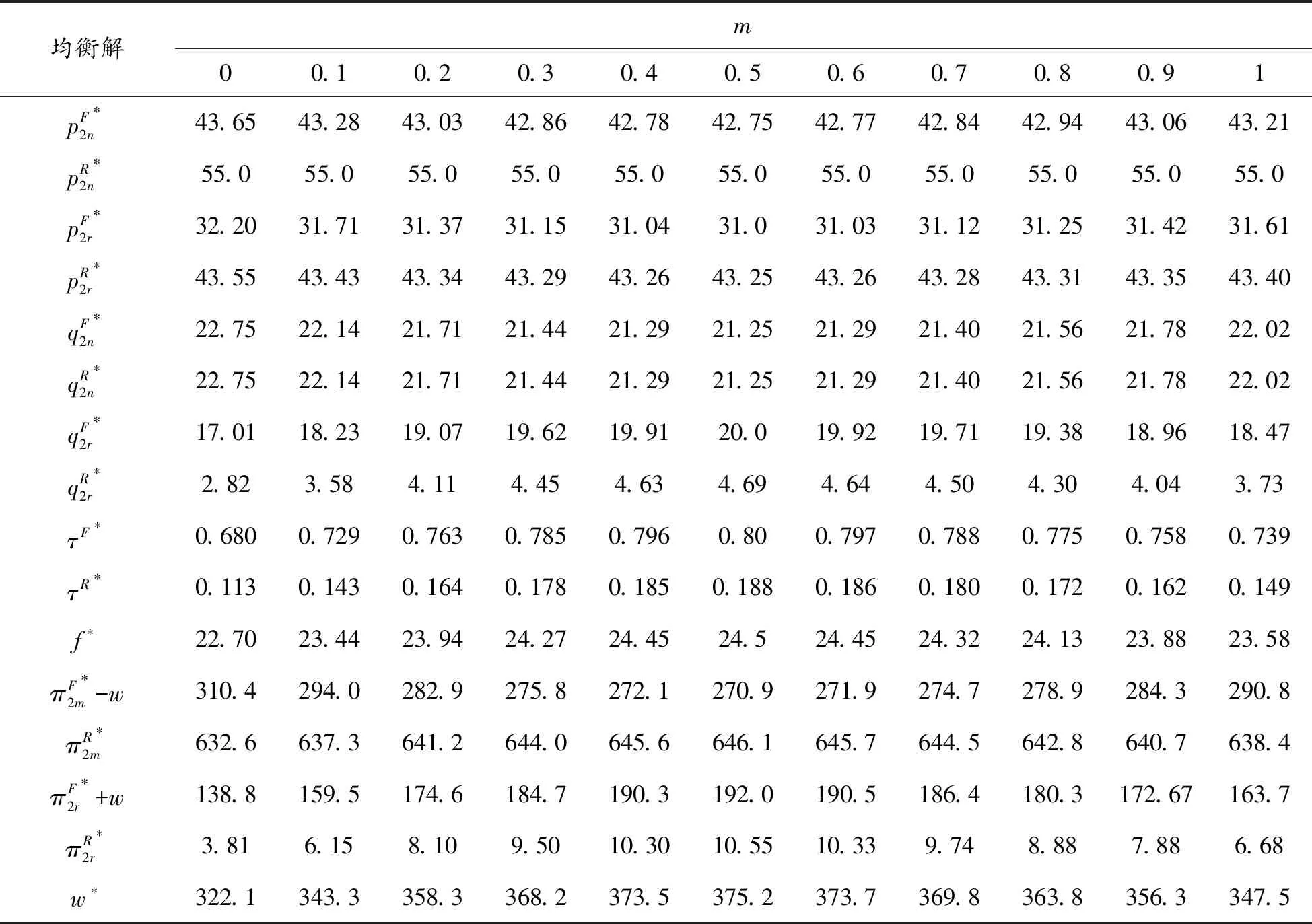
表2 回收质量m对均衡解的影响

分析表2可知：

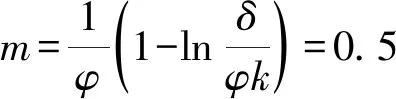
2) 2种专利许可策略下旧产品的回收率和再制造商的利润均随着回收质量的增加先增大再减小，且在m=0.5时达到最大，这与命题1是一致的，说明当再制造商在最佳回收质量时回收不仅可以获得最大的利润，而且对环境保护也有利。

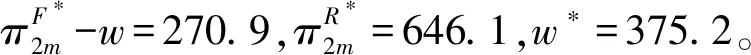
4) 从消费者和环境保护的角度来看，固定费用专利许可策略会优于单位费用专利许可策略，这是由于固定费用专利许可策略下新产品和再制造品的价格小于单位费用专利许可策略，且固定费用专利许可策略下旧产品的回收率大于单位费用专利许可策略，与命题4相符。

5 结束语

本文针对由一个原始制造商和一个再制造商组成的两周期闭环供应链模型，探讨在回收质量不确定时制造商的最优专利许可策略以及回收质量对制造商与再制造商相关决策的影响。

研究结果表明：① 对于再制造商来说，无论制造商选择哪种专利许可策略，再制造商的最佳回收质量是不变的，回收该质量的旧产品可以获得最优的利润。② 从消费者和环境保护的角度来看，当制造商选择固定费用专利许可策略且再制造商以最佳回收质量进行回收再制造时，新产品和再制造产品的价格是最低的，而且旧产品回收率是最高的，此时对消费者和环境保护是最有利的。③ 对于原始制造商来说，选择哪种专利许可策略存在临界值。当固定专利费用大于该临界值时，制造商应选择固定费用专利许可策略；反之，则应选择单位费用专利许可策略。而且该临界值会随着回收质量的增加先增大后减小且在最佳回收质量处达到最大。这说明若要原始制造商选择固定费用专利许可策略，则此时的固定费用是最高的。

需要指出的是本文假设制造商与再制造商之间的信息是完备的，制造商与再制造商之间属于完全信息下的动态博弈。但现实中企业之间总有一些信息是隐藏的，所以进一步的研究方向可以基于制造商与再制造商之间不完全信息下的动态博弈。