不同边界条件断层端部应力集中效应及 对裂缝发育的启示

邱登峰,云金表,刘全有,周 雁,宁 飞,宋海明

(1. 页岩油气富集机理与有效开发国家重点实验室，北京 100083； 2.中国石化 石油勘探开发研究院 构造与沉积储层实验室，北京 100083)

构造应力场对裂缝的形成、活化、裂缝渗透率与流体渗流具有重要影响[1-3]。断层是地壳中最重要的构造类型,是造成岩体中应力发生复杂变化的主要因素之一[4]。断层的形态、规模、活动性、所处的应力状态、与最大主应力轴的夹角等都会对应力场产生不同形式、不同程度的扰动[1,5-9]。从断层的形态上,断层的交叉、分枝及拐点部位多产生应力集中现象,这些部位应力强度明显高于邻区[4]。从断层的规模上,通过断层周边应力场的原位实测及数值反演,认为应力场的扰动范围与断层的几何尺寸密切相关[8]。从断层所处的应力状态入手,Ghislain等结合光弹性法和数值模拟,研究了不同几何学的断层模型在双轴挤压载荷下的应力场展布,旨在展现断层典型的双轴应力场特征[1]。在最大主应力方向与断层应力场的关系上,根据中国西南地区5级以上的地震统计数据,认为区域最大主压应力在与断层面成30°～ 60°夹角时,断层应力集中程度最大[10],前人还采用有限元数值模拟和弹性力学解析解的方法对该问题也进行了初步探讨[6-7,11]。但是,不同学者关于不同主应力方向下断层端部应力场的变化趋势存在明显差异,断层端部应力集中的分布形态,影响范围与影响因素也有待深入研究,这些问题对致密储层和页岩油气的勘探开发具有重要意义。对勘探而言,与应力集中相关的裂缝发育区是致密油气、页岩油气的有利指向区[12-15]；对开发而言,致密储层、页岩气储层必须经压裂才能形成工业气流[16-17],但由于断层对应力场的扰动,压裂时人工裂缝走向会发生偏离,因此井网布置等开发方案的制定需根据实际应力场展布进行[6]。

本文拟以光弹性物理模拟和有限元数值模拟为技术手段,设计一系列对比试验,探讨了均质条件不同主应力强度、不同主应力方位下断层端部应力场的平面展布规律,研究断层端部应力集中效应与最大主应力方位的相关关系,并根据弹性力学理论分析实验结果,解析断层端部应力场的分布机理。

1 分析测试方法

1.1 分析方法

为研究断层应力场,本文采用了光弹物理模拟和有限元数值模拟的对比研究方法。光弹性物理模拟法应用光学原理研究弹性力学问题,当具有双折射效应的透明模型材料被置入平面偏振光场并承受载荷时,光路中会产生反映受力模型应力分布的干涉条纹图[18],具有直观、全场分析等优点,是进行应力场研究的有效方法,被国内外一些知名的研究机构和学者广泛采纳[19-26]。有限元法是构造应力场数值模拟的重要方法之一,是一种计算应力应变比较成熟的模拟方法[27]。

1.2 物理模拟

实验采用的光弹性材料由环氧树脂、顺丁烯二酸酐、邻苯二甲酸二丁酯按100 ∶30 ∶5的比例配制而成[25]。为表征断层,首先将厚度为5 mm的平面光弹性基体板材切割为10 cm×10 cm的方块,然后采用高精度的数控加工设备用0.6mm的铣刀用均匀切割的方式以模型的几何中心开一个宽0.6 mm,长3cm的贯通槽(图1a),用于模拟切穿盖层的断层。断层与水平方向夹角分别为0°,15°,30°,45°,60°,75°,90°,共7个模型。边界外力为垂直方向上施加的挤压应力,强度为1 000,2 000,3 000 N。为避免初应力影响实验观察,将模型在烘箱中油浴加热消除初应力。

光弹性实验在中国石化石油勘探开发研究院构造与沉积储层实验室PH-400型(光场直径4 00 mm)非球面准直光弹仪上进行。为方便观察,通过合理配置光路中偏振片及1/4波片的组合关系,采用高清数码相机分别采集了不同模型在不同挤压应力条件下消除等倾线后反映主应力差值的等差线干涉条纹。光测弹性力学中,主应力差与等差线条纹级次遵循如下关系式[28]：

(1)

式中:σ1,σ2为最大、最小主应力,Pa,以张应力为正,压应力为负；f为光弹模型的材料条纹值,N/cm；d为模型厚度,cm；n为等差线条纹级数,在f和d恒定时直接反映差应力大小。

本文的断层模型属没有外力作用的自由边界,只有一个与边界切线同向的主应力[29]。因此,在断层端部,公式(1)可简化为：

(2)

σ1或σ2需根据钉压法来确定。在垂直于模型的边界上,对研究的某点施加一个微小的法向压力,若等差线条纹级数增加或向条纹级次低的方向移动,则钉压点的边界应力为第一主应力σ1(张应力),反之亦反[30]。

1.3 数值模拟

数值模拟以有限元分析软件Ansys为技术平台。为与光弹物理模拟的结果比对,数值模型与物理模型完全一致(图1)。模拟时采用PLANE2单元将几何模型离散成若干个连续的三角形网格,方形面单元网格化的节点间距为10 mm,断层边缘和端点的网格单元进行了加密(图1b)。每个网格单元被定义为各向同性的线性弹性体,它们的力学参数采用光弹性材料的弹性模量和泊松比。在室温下,国内常用光弹性环氧树脂的泊松比为0.35～0.37,模拟时采用中间值0.36,弹性模量为3.3×104～3.5×104kg/cm2[31],模拟时采用中间值3.4×104kg/cm2(3 332 MPa)。

图1 物理模型(a)与有限元模型(b)Fig.1 Physical model(a)and finite element model(b)

2 结果

2.1 断层端部的应力性质与大小

为确定断层端部的应力性质,本文以15°模型为例,在1 000 N的垂向挤压载荷下,对断层左端进行了钉压实验。为便于观察等差线条纹的移动,以白光为光源采集了钉压前后彩色的等差线条纹(图2a)。由于钉压的附加应力远小于边界载荷应力,故条纹移动不明显。为判断条纹的移动方向,在等差线条纹图中测量了二级条纹红色区域在垂直方向上的最远跨度,钉压前该值A1A2=31.13 mm(图2a),钉压后该值B1B2=30.68 mm(图2b),等差线条纹向内收缩1.45%,即向条纹级次高的方向移动,表明断层端部为压应力。

根据没有外力作用的自由边界都处于单向应力状态的基本原理及钉压法实验,在测定模型厚度及通过对径受压圆盘的预实验,求取模型的材料条纹值(201.70 N/cm)后,可根据公式(2)通过等差线条纹级数计算断层端部的压应力(表1)。以15°模型1 000 N载荷为例,断层左端点的压应力为10.09 MPa,端点外的非应力集中区主应力差小于3.36 MPa。在数值模拟中,断层端部的压应力可达70～165 MPa,应力集中区以外的差应力为0.8～20 MPa。由此可见,在非应力集中区,物理模拟与数值模拟显示的差应力数值相当,而在断层端部的应力集中区,数值模拟数值远大于物理模拟。可能原因在于,物理模拟的主应力大小主要通过等差线条纹级次反映,在断层端部,尽管有很强的应力集中效应,但由于分辨率的影响,导致测定的条纹级次偏低,因而转化出的主应力值较低。

图2 15°模型在1 000 N载荷下钉压实验前(a)后(b)断层左端的等差线条纹Fig.2 Isochromatic fringe patterns at fault’s left end of the 15°model under 1 000 N load before(a)and after(b)nail pressure test

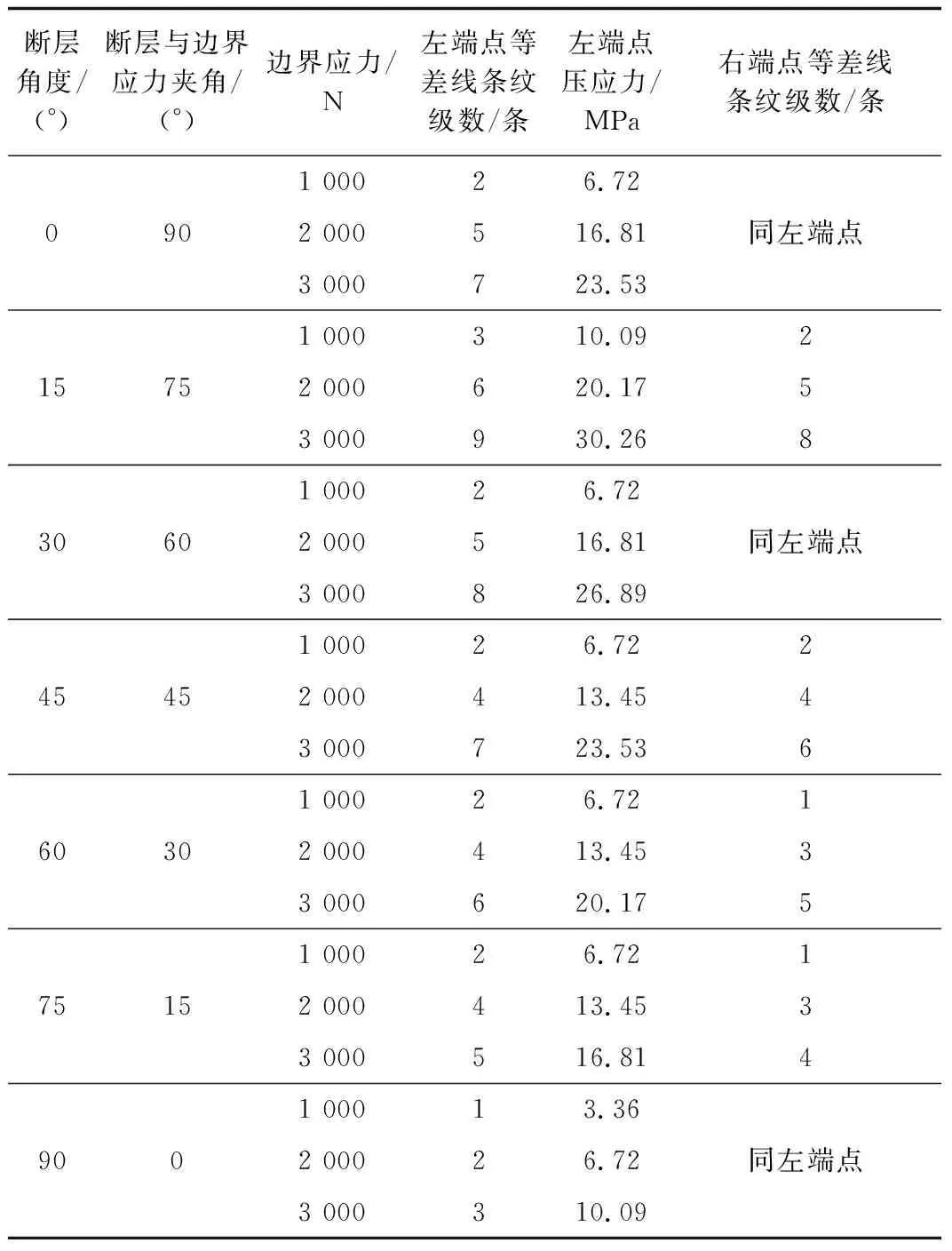
断层角度/(°)断层与边界应力夹角/(°)边界应力/N左端点等差线条纹级数/条左端点压应力/MPa右端点等差线条纹级数/条0901 00026.722 000516.813 000723.53同左端点15751 000310.0922 000620.1753 000930.26830601 00026.722 000516.813 000826.89同左端点45451 00026.7222 000413.4543 000723.53660301 00026.7212 000413.4533 000620.17575151 00026.7212 000413.4533 000516.8149001 00013.362 00026.723 000310.09同左端点

2.2 断层端部的应力展布特征

断层端部的集中应力呈现8字形展布(图3a),以断层端部圆弧最凸出端点为“8”字的腰部交点(图3a中的A点),以圆弧两端弧线与直线边界的连接点为中心以双曲线形式向外成展开状延伸(图3弧形线)。在双曲线的展布路径上,离断层端部越近的区域条纹级次越高,差应力越大,控制范围越小。相同模型的数值模拟也显示出类似特征(图3b),如B点的应力集中区向断层端部明显缩进,但8字形展布特征及双曲线的延伸形态不如物理模拟结果明显,表明在物理模拟分辨率可达到的范围内,物理模拟对应力结果的表达更直观。

断层端点的左侧与右侧、上侧与下侧的应力分布也不尽相同。模拟结果显示,断层左端条纹级数高于右端(图4),15°,45°,60°,75°模型均如此(表1)。以60°模型3 000 N载荷为例,断层左端点显示清晰的6级条纹,而右端点仅可见5级条纹。且左端点同级次等差线条纹的控制范围大于右端点(图4a,b),30°,90°模型也类似。因此,物理模拟中断层左端点的应力集中效应强于右端点。在0°,15°,45°三个数值模型中,15°和45°数值模型的最大值均出现在左侧(图4c,d中的MX位置),仅0°数值模型的最大值出现在右侧,可能与0°模型右侧尖端曲率大于左侧有关。在相同端点的上下侧对比中,下侧应力集中大于上侧。图4a和图4b显示高级次条纹更容易出现在端部下侧,且端部下侧条纹的控制范围大于上侧。

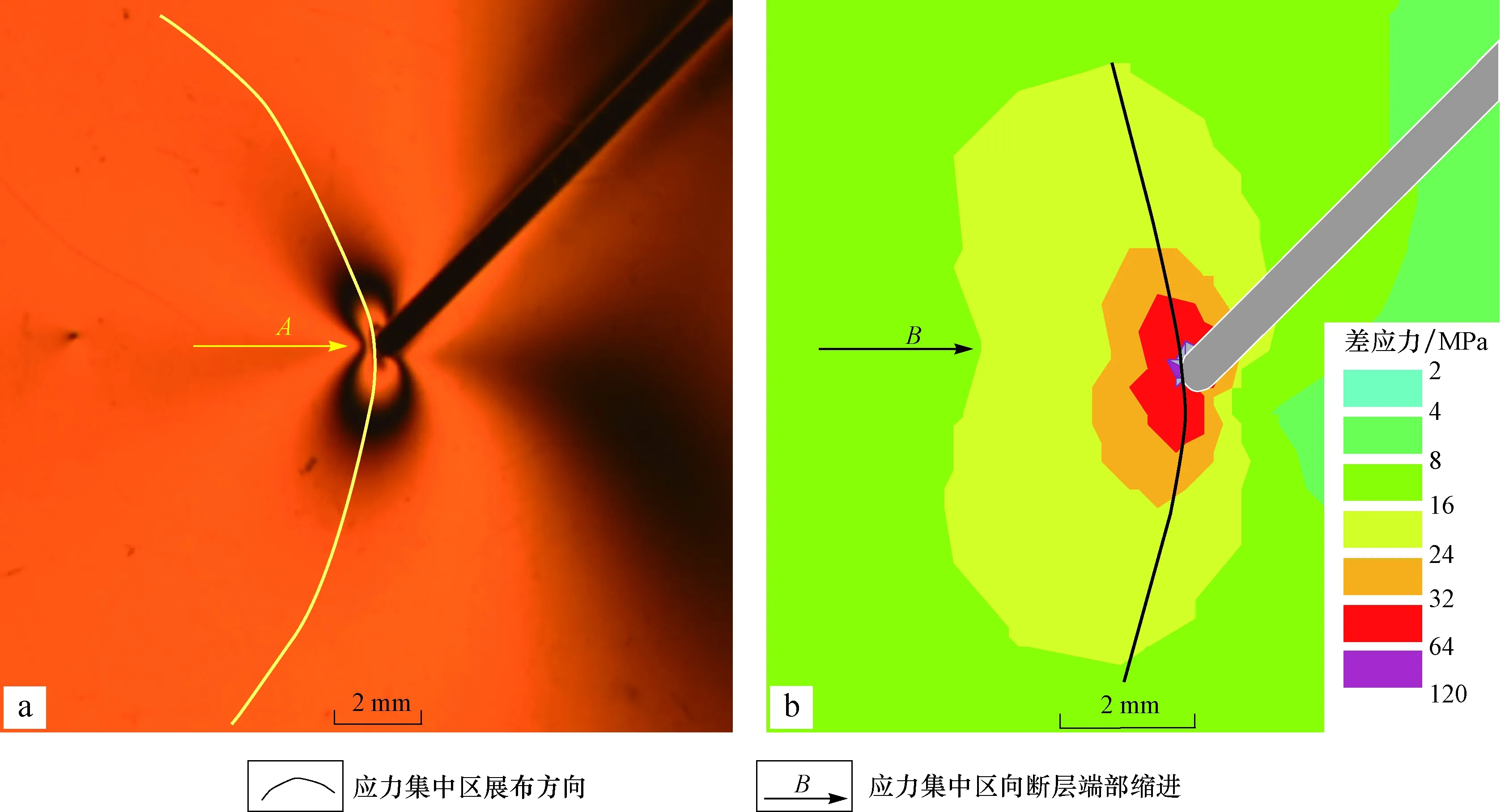
图3 光弹物理模拟和有限元数值模拟中断层端部应力集中区域的展布特征Fig.3 Distribution characteristics of stress concentration at fault’s end in photoelastic physical modeling and finite element simulationa. 45°模型在1000N挤压载荷下的等差线条纹图;b.该模型数值模拟的差应力云图

2.3 边界应力强度与方位对断层端部应力的影响

不同大小边界载荷下的模拟结果显示,边界载荷越大,断层端部的等差线条纹级次越高(表1),应力集中效应越明显。同一模型断层端部的等差线条纹级次与边界载荷大小呈现出良好的线性关系(图5a),拟合系数大部分达到1,表明等差线条纹级数是模型接受边界载荷的优秀指标。

当断层走向与边界应力方位的夹角在0～90°范围内变化时,随两者夹角增大,在3种不同载荷下断层端部的压应力均呈整体增强的趋势,在夹角为75°时达到最强(图5b)。无论物理模拟还是数值模拟,图6均清晰地显示在45°,75°,90°等不同夹角时,75°时压应力最强。如在1000N载荷下,当断层走向与边界应力夹角为75°时物理模拟的等差线条纹级次最高,控制范围最大(图6a15),数值模拟中仅在75°时断层端部出现153～165 MPa的最强压应力值(图6b15)。

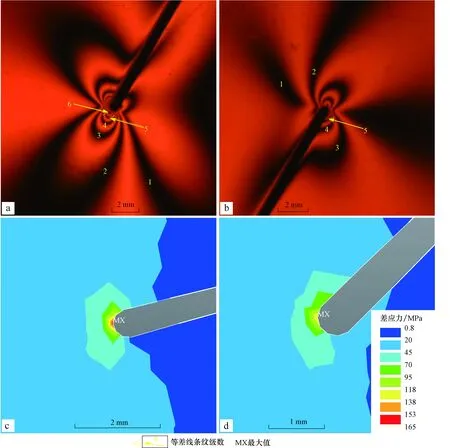
图4 光弹物理模拟和有限元数值模拟中断层端部不同部位的应力分布Fig.4 Stress distribution of different parts around fault’s end in photoelastic physical modeling and finite element simulation a,b. 60°模型在3 000 N载荷下断层左端(a)和右端(b)的光弹性等差线条纹图；c,d. 15°模型(c)、45°模型(d)在1 000 N 载荷下数值模拟的差应力云图

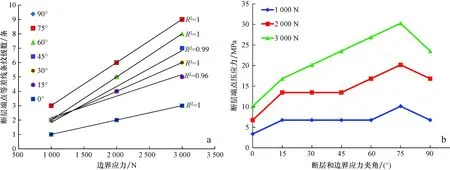
图5 断层端部应力与边界应力强度(a)以及断层端部应力与方位(b)的关系Fig.5 Relationship between compression stress at fault’s end and boundary stress intensity(a)and between compression stress at fault’s end and orientation(b)a.断层走向与边界应力不同夹角时等差线条纹级数与边界应力强度的关系；b.不同应力强度下断层端点压应力与断层走向和边界应力夹角的关系

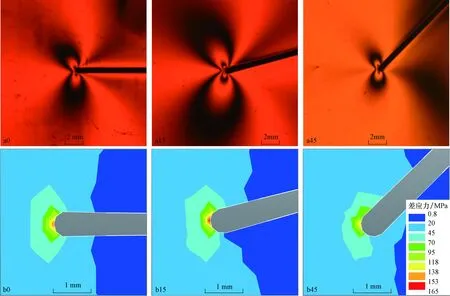
图6 光弹物理模拟和有限元数值模拟中边界应力与断层走向不同夹角时断层端部的应力分布Fig.6 Stress distribution at fault’s end under various angles between boundary stress and fault strike in photoelastic physical modeling and finite element simulation(边界应力与断层走向夹角为90°时的结果为a0,b0；夹角为75°时的结果为a15,b15；夹角为45°时的结果为a45,b45。其中,a0,a15,a45为单色光下的光弹性等差线条纹图；b0,b15,b45为有限元数值模拟的差应力云图；它们分别具有相同的图像比例)

3 讨论

3.1 断层端部应力场的机理

模拟结果显示,断层端部应力在断层走向与边界应力方位夹角为75°时达到最强,与前人研究结果显著不同。如刘中春等[11]通过理论计算和数值模拟,认为当断层走向与边界应力夹角为90°时断层端部的压应力最大；而沈梅超等[6]、孙礼健等[7]通过数值模拟,认为该夹角为45°时断层端部的应力集中效应最强。不同学者认识大相径庭的原因在于,断层建模时模拟断层的方式不同。

刘中春等采用了椭圆孔口模型来模拟断层,对椭圆孔口进行应力分析,通过保角变换和复变函数运算[11],得到椭圆孔口上任意一点切向应力的弹性力学理论解为：

(3)

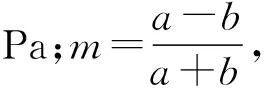
借用公式(3),假定在本文的边界条件下采用椭圆孔口模型模拟断层,在断层端部即椭圆长轴的顶点,θ=0,边界条件中水平方向上的边界应力为0,故q1=0,在考虑断层与最大主应力夹角α对断层边界切向应力影响时,断层形态即椭圆形态一经确定,m可视作为常数,因此,公式(3)可简化为：

σθ=k1cos2α+k2

(4)

沈梅超等[6]和孙礼健等[7]采用矩形孔口模型模拟断层,矩形孔口的孔边应力数值解比椭圆孔口模型要复杂得多。

对图7所示力学模型,根据平面孔口弹性力学的复变函数理论,可按下式计算矩形孔口边缘任意点z的边界应力[32]：

(5)

(6)

(7)

式中,σx,σy为正应力,Pa；τxy为剪应力,Pa；φ(z)和ψ(z)为矩形孔口外的解析函数；φ′(z)与φ″(z)为φ(z)

图7 断层矩形孔口的力学模型Fig.7 Mechanical model showing the rectangular orificeof a fault

因此,利用复变函数理论的共形映射技术求出解析函数φ(z)和ψ(z)解析式,是开展矩形孔口边缘应力计算分析的核心。将含矩形孔的无限域映射到单位圆内的映射函数可采用如下形式[33-34]：

(8)

式中:ζ为单位圆外任意点；ω(ζ)为将单位圆外域共形映射到孔口外域的映射函数,以Laurent级数有限项给出,展开级数越高,所得孔边曲线与精确矩形的差别越小；m为映射函数的项数;c是复常数,与矩形孔的大小有关；β1,β3,…与矩形孔的边长比有关。

运用上述方法,杨丽红等(2002)研究了矩形孔口在单向应力状态下的孔边应力。结果显示,单向拉伸时,在图7所示的α=0°,45°,90°三种状态下,孔边峰值应力在45°时最大，90°时居中,0°时最小[33]。因此,当通过矩形孔口模型模拟断层时,断层端部的应力集中效应在断层走向与边界应力夹角为45°时达到最强。

本文采用了断层端部为弧形中部为长方形的孔口模型模拟断层,按照公式(5)—(7)的复变函数理论和公式(8)的映射技术,理论上也能求出本文断层模型的数值解。从前两种断层模型的数值解与模拟的一致性来看,本文物理与数值模拟所得结果也应是合理的。

因此,断层形态及模拟时的建模方式对断层周缘应力场有重要影响。

3.2 断层应力集中效应的构造意义

从模拟结果看,断层端部8字形应力集中区控制范围受区域应力强度、区域应力与断层夹角、断层形态影响较大。若构造活动的强度越大,或在双曲线展布的延伸方向上,越靠近断层端部的8字形区域,应力集中效应越明显。在断层端部8字形的应力集中区内,断层左端应力集中效应高于右端,下侧大于上侧。产生该现象可能存在两种原因：第一,物理模拟时在模型顶面施加均布载荷的加载面可能向左倾斜而非完全水平,因而模型左侧承受的压应力大于右侧,造成了在多个模型左端记录的应力大于右端的系统误差,但是0°模型物理模拟左右端点的等差线条纹级次与控制范围相同。第二,离固定端越近的断层端承受的应力越大。模拟时,除0°模型断层左右端与底部固定端等距外,在将断层按不同角度逆时针旋转后,相对断层右端,其他模型的断层左端与固定端更接近,因而应力集中效应更明显。对同一端点的上、下侧,下侧比上侧更靠近底部固定端。靠近固定端应力更容易集中的可能原因为,远离固定端时,应力尚能通过变形向前方传递,而越接近于固定端,能产生的变形量越小,因而应力集中效应更强。在脆性的小变形范围内,根据岩石破裂理论,在应力越集中的地区,岩石越容易破裂产生裂缝。

断层端部应力集中区以双曲线形式在断层两边呈8字形展开(图3a),提示脆性断层可能按如下方式扩展(图8),当初始断层在地质体的薄弱部位形成后,会优先选择沿应力集中区的双曲线展布方向扩展。中国大地构造纲要图显示,断裂构造带往往呈弧形弯曲分布,特别是在中国西部以挤压构造为主的地区,本文实验中断层端部应力集中区的展布形态从一定程度上解释了在构造环境相对稳定并无砥柱阻挡的条件下脆性断层呈弧形展布的原因。

对与断层相关的裂缝性储层而言,图3a所示断层应力集中区指示了与断层相关的裂缝性储层可能的发育部位。Kattenhorn总结了与本文非常类似的断层末端应力场分布示意图,并以法国南部朗格多克一处野外露头灰岩断层中的裂缝发育为例说明了该示意图的合理性[35]。Yufutsu气田是日本最大的气田之一,为典型的致密气藏,Tamagawa通过成像测井发现A，C两口高产井比B，D两口干井的宏观裂缝更发育,由于这四口井均位于断层附近,他们通过位移不连续的边界元方法模拟了这四口井附近的应力场,发现两口高产井均位于断层末端8字形的应力集中区,而两口干井位于该应力集中区之外,因此认为应力集中通过开启或生成裂缝,提高了储层的渗透率,并提出断层端部的应力集中区是裂缝储层油气勘探开发的高潜力区[36]。

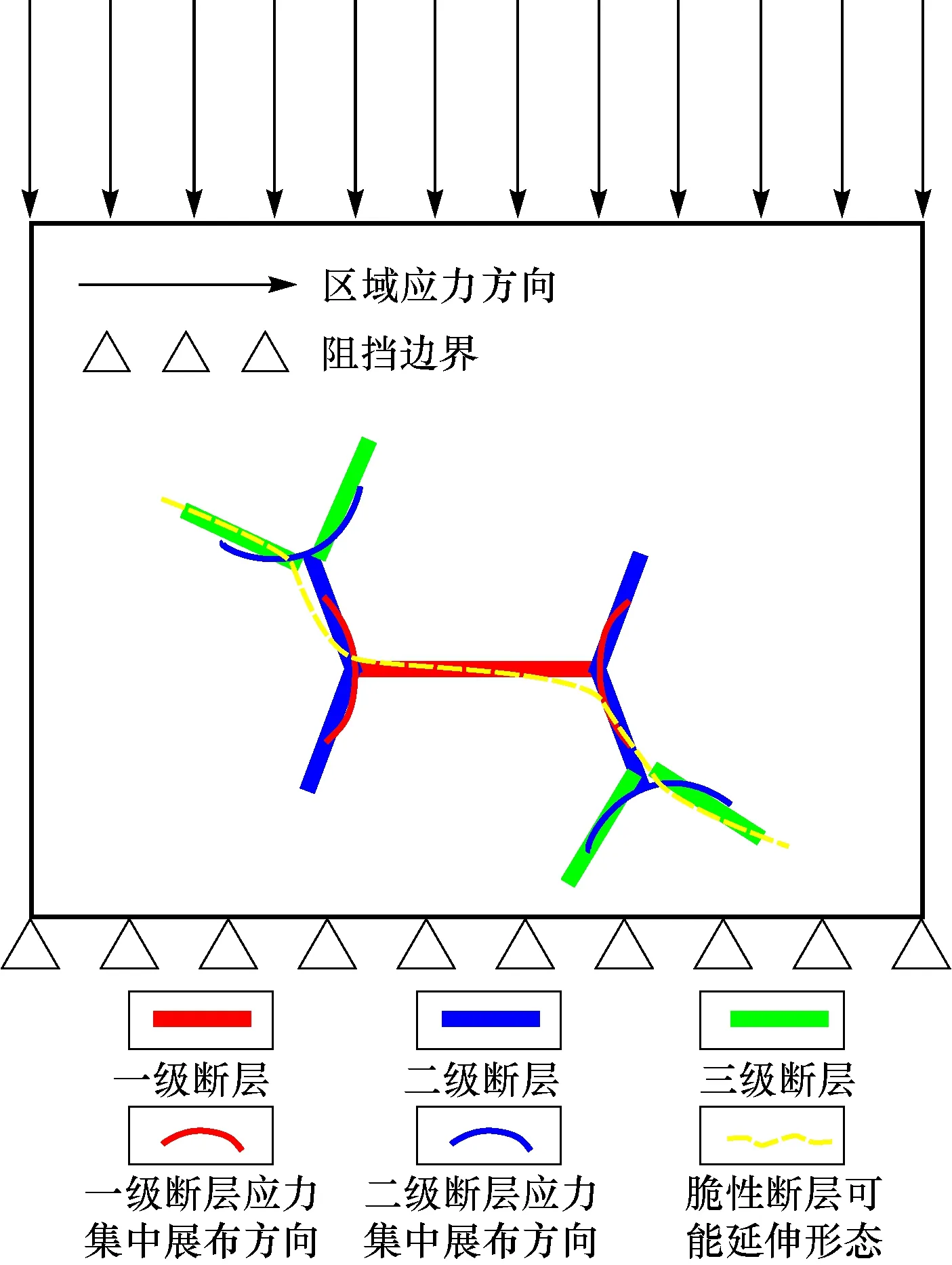
图8 脆性断层扩展示意图Fig.8 Schematic diagramshowing the expansion of brittle faults

在本文单轴压缩的条件下,当边界应力与断层走向为75°时断层端部应力集中效应最为明显,亦即断层扩展和裂缝发育的优势方位。Blenkinsop通过理论计算和随机模拟,得到了类似的结论。他们发现,在单向应力条件下,断层走向与边界应力夹角70°～80°在2 000条随机断层的方位分布中处于最优地位[37]。通过对比利牛斯山脉南段的Larra逆冲断层解剖,发现在Pierre-Saint-Martin地区的灰岩层中,大部分(95%的置信区间)的裂缝充填脉分布在逆冲断层与最大主应力成66°±17°的范围内[37-38]。上述研究成果从断层分布方位的理论推导和裂缝的野外描述两方面为本文实验模拟得到的75°时应力集中效应最为明显提供了例证。

4 结论

1) 挤压背景下断层端部呈现压应力集中,该应力集中区以断层端部圆弧最凸出端点为中心以双曲线形式向外呈“8”字形展开状延伸,其控制范围随边界应力强度增加而增大。

2) 断层端部应力随断层走向与边界应力方位夹角增大呈整体增强的趋势,在75°时最大,断层形态及模拟时的建模方式对断层端部应力场有重要影响。