玩转方差 统计无忧

文

统计是初中数学中几大主要板块之一，其中“方差”是同学们最容易犯错、最怵的统计知识点，究其原因是其计算量大，公式繁琐。本文旨在帮助同学们剖析方差，厘清相关策略方法。当你能够玩转方差的时候，那你的统计无忧矣。

一、据方差性质解决问题

例1 下图是甲、乙两人在一次射击训练中击中靶的情况（击中靶中心的圆面为10环，靶中各数字表示该数所在圆环被击中所得的环数），每人射击了6次。

（1）请用列表法将他俩的射击成绩统计出来；

（2）若选派其中一人参赛，你认为应选哪人？请说明理由。

【解析】（1）根据两人击中靶的情况列表。

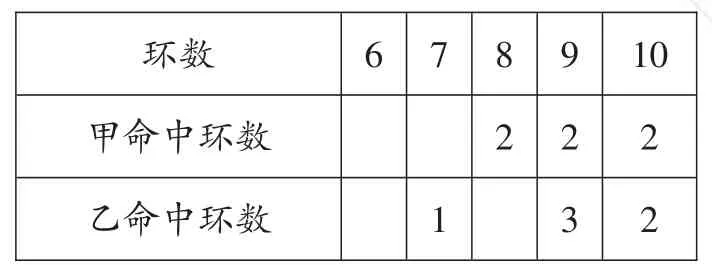
10 6 7 8 2环数甲命中环数乙命中环数1 9 2 3 2 2

（2）先求出两人射击成绩的平均数，再求出两人成绩的方差＜s2乙，可知甲与乙的平均成绩相同，但甲发挥得比乙稳定，所以选甲参赛。

【点评】比较两人的成绩，首选平均数这个指标，平均数相当再选择方差，因为方差反映了一组数据的波动大小，方差越大，波动性越大，方差越小，稳定性越好。

二、变化数据的方差概括

例2 一组数据a，b，c，d，e的方差是3，则新数据2a+7，2b+7，2c+7，2d+7，2e+7的方差是________________ 。

【解析】设一组数据a，b，c，d，e的平均数为m，则新数据2a+7、2b+7、2c+7、2d+7、2e+7的平均数为2m+7，方差为+7-2m-7）2+（2b+7-2m-7）2+（2c+7-2m-7）2+（2d+7-2m-7）2+（2e+7-2m-7）2］=4×［（a-m）2+（b-m）2+（c-m）2+（d-m）2+（em）2］=4×3=12。

【点评】将一组数据按照一定规则进行转化，他们的平均数、方差是有章可循的。

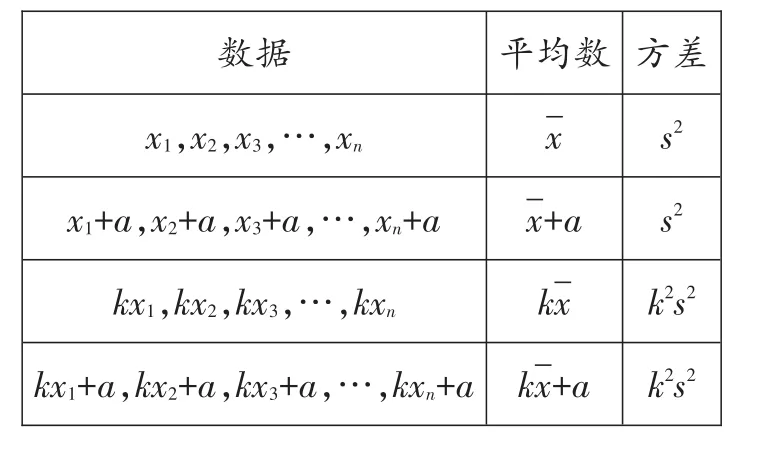
数据 平均数 方差x，x，x，…，xxs2 123n x+a，x+a，x+a，…，x+ax+as2 123n kx，kx，kx，…，kxkx k2s2 123n kx+a，kx+a，kx+a，…，kx+a kx+a k2s2 123n

三、运用整体思想求方差

例3 某学习小组5位同学参加初中毕业生实验操作考试（满分20分）的平均成绩是16分。其中三位男生的方差为6（分2），两位女生的成绩分别为17分，15分。则这个学习小组5位同学考（a-16）2+（b-16）2+（c-16）2］=6，则（a-16）2+（b-16）2+（c-16）2=18，即可得这个学习小组5位同学考试分数的方差［（a-16）2+（b-16）2+（c-16）2+（17-16）2+（15-16）2］

【点评】由于不知道三位男生的成绩，故无法直接求该小组成绩的方差，先利用方程思想得到关于三位男生方差的方程，最后运用整体思想代入即可求解小组的方差。试分数的方差为________。