涡脱落热声振荡中相似性及涡声锁频行为*

王伟 出口祥啓 何永森 张家忠†

1) (西安交通大学能源与动力工程学院,西安 710049)

2) (德岛大学大学院理工学研究部,德岛 770-8506,日本)

基于Matveev和Culick提出的涡脱落引起的热声不稳定性一维简化模型,对涡脱落引起的热声振荡中的典型非线性现象进行研究,着重研究了系统的初值敏感性、关键参数对热声振荡的影响规律及涡声锁频现象.首先,采用Galerkin方法将控制方程中压力和速度波动在基函数下展开,使偏微分方程组转化为一簇常微分方程；然后,数值求解得到了不同系统参数下声场的压力和速度波动,并详细分析了系统在不同初始条件下的热声不稳定性,同时研究了不同稳态流动速度对系统热声振荡的影响规律,以及在不同稳态流动速度下热声振荡过程中出现的涡声锁频现象.结果表明：该涡脱落热声振荡系统对初值极为敏感,是典型的非线性系统；随着稳态流动速度增大,压力波动的振幅总体有增大趋势,但在几个速度区间内却重复出现振幅先减小后增大的相似结构；系统最终以涡撞击频率(fs)的整数(fp/fs)倍做周期振荡,呈现转数为fp/fs的涡声锁频,该涡声锁频可以作为周期性燃烧振荡的重要特征.

1 引 言

反应物在燃烧室内燃烧过程中伴随着显著的压力振荡,若该压力振荡由不稳定热释放引起,则该现象被称为燃烧不稳定.此类现象广泛存在于许多实际系统或设备中,如：冲压式喷气发动机、火箭发动机、加力燃烧室、燃气轮机以及锅炉.该燃烧不稳定性是由热源不稳定放热引起的声场振荡,又被称为热声不稳定性或热声振荡,其表现为热释放和压力的快速波动,以及燃烧室一种或多种声学模态的大幅度振荡.各种燃烧室内的燃烧振荡将带来许多令人困扰的问题,如：其产生的大幅度压力和速度振荡,将导致喷气发动机推力振荡；其产生的严重振动,将干扰控制系统的运行；燃烧振荡将加重燃烧室壁面的热应力；燃烧振荡将加大系统组件的机械负载,引起低周或高周疲劳；燃烧振荡可能导致燃烧室熄火或火焰闪回[1].因此研究热声不稳定性现象,揭示其发生机理与发展规律,对兴利避害,合理利用热声振荡具有重大意义.

热声不稳定性是由波动的热释放率与燃烧室声场之间形成正反馈回路而引起的,即：反应物燃烧造成的不稳定热量释放引起声场的振荡,而声场的振荡又反过来加剧热量释放的波动过程,从而形成正反馈回路[2].文献[1]对热声振荡的产生机理给出了解释：燃烧过程向声场振荡中添加(或移除)能量取决于Rayleigh积分的正(或负),Rayleigh积分的正负取决于压力波动与热量释放间的相位差,该相位差小于90°,相应的Rayleigh积分为正,燃烧过程向声场振荡中加入能量.若加入的能量大于燃烧室中传热、辐射、对流及黏性耗散等消耗的能量,振荡将逐渐加强,直至趋向某一极限环振荡.

事实上,热声振荡是由非线性过程主导的复杂现象,Rayleigh准则和线性分析方法虽然能够解释热声振荡产生和维持的机理,但却无法预测系统失稳后的状态,也无法对热声振荡中可能存在的模态耦合、锁频、迟滞、分岔及混沌等复杂非线性现象进行分析,因此有必要采用非线性动力学分析方法研究热声振荡.

对于该问题的研究,在基本模型方面,Rijke管是研究热声振荡的最方便最经典的模型,因此一些学者基于该模型对热声振荡进行了大量研究,其中不乏采用非线性动力学方法进行的研究.Balasubramanian等[3]就以一维Rijke管热声振荡模型为研究对象,数值研究了热声不稳定过程中的非正常和非线性现象.Subramanian等[4]对水平Rijke管的动力学行为进行了分岔分析,采用数值延拓法得到了包含不稳定极限环振幅的分岔图,并对不同参数下的亚临界分岔和双稳态区进行了分析.党南南等[5]采用数值方法研究了强弱两种阻尼条件下Rijke管热声振荡稳定性切换行为与传热迟滞时间的关系.

基于以上背景,本文研究基于Rijke管的带后向台阶的模型,该模型就是一种火焰稳定器,在实际燃烧室中很常见.早在1956年,Rogers等[6]就对一小型二维燃烧室进行实验研究,观察了高频振荡伴随的火焰稳定器边缘周期性涡脱落,提出了振荡发生的机理.后来,许多学者通过大量的实验研究了涡脱落在热声振荡中的作用[7-11].同时,随着计算流体动力学(CFD)技术的发展,学者们开始用CFD软件模拟燃烧-涡-声相互作用的过程[12,13].如今,大涡模拟(LES)成为了数值模拟燃烧过程及燃烧不稳定性的最有力工具[14-17].

目前对带后向台阶燃烧室的热声振荡研究主要以实验和数值模拟为主,理论研究和机理分析较少.由于实验和数值研究消耗大量资源和时间,因此有必要基于基本模型的研究,给出涡脱落热声振荡产生的机理及演化规律.在此方面,学者们做了许多研究.Matveev和Culick[18]基于带后向台阶燃烧室的简化模型推导出了涡脱落、燃烧室声场和燃烧过程之间相互作用的降阶模型,并用该模型计算了热声振荡过程的锁频,与实验结果进行了对比验证,同时指出该简化模型可以模拟许多真实燃烧室中存在的模态耦合、锁频、迟滞及混沌等非线性现象.Tulsyan等[19]以Matveev提出的模型为基础,数值计算了不同参数下系统热声振荡的时间序列,对比了初始扰动、阻尼系数等系统参数对热声振荡的影响.文献[20-22]均基于该涡脱落引起的热声振荡简化模型对涡脱落、声场与燃烧过程相互作用中的非线性现象进行了研究.Singaravelu和Mariappan[23]对该模型的控制方程进行了无量纲化,并做了线性稳定性分析,导出了热声振荡过程中的庞加莱截面计算公式,得出系统的稳定性与庞加莱映射的特征值有关的结论,量化了该热声相互作用的稳定性.Singaravelu和Mariappan[24]进一步基于该无量纲化控制方程,研究了燃烧不稳定性中的涡声锁频现象,以系统中速度波动量从零到峰值的幅度作为判断Helmholtz数从旋涡脱落模式向声模式转变的标准,提出了判断涡声锁频的准则并与实验结果进行了比较.Chakravarthy等[25]通过实验研究了后向台阶燃烧室中的涡声锁频现象,结果表明涡声锁频是燃烧不稳定性出现的重要标志.

目前为止,基于Matveev和Culick[18]提出的涡脱落热声模型的研究,虽然分析了某些关键参数对系统的影响,以及发现了涡声锁频等非线性现象,但是没有研究燃烧室主流流速对系统热声振荡过程的影响规律,也没有从非线性动力学角度对实验中发现的涡声锁频现象的机理进行分析.因此本文以此为背景,首先介绍了所研究的物理模型及控制方程,然后采用Galerkin方法逼近控制方程,取前十阶模态进行数值计算,得到了声场的压力和速度波动.对比不同参数下的计算结果,首先研究了系统的初值敏感性,证实了其为典型的非线性系统；然后研究了主流平均流速对热声振荡的影响规律,发现了平均流速改变下压力波动振幅呈现相似结构；最后通过频率比研究了系统热声振荡中涡声锁频的特点,揭示了实验中发现的涡声锁频的形成机理.本文主要研究了涡脱落引起的热声振荡中相似性和涡声锁频这两种典型非线性现象,对于从动力学角度揭示热声不稳定性的机理及指导相关实验具有重要意义.

2 数学物理模型及求解

2.1 物理模型

如图1所示,采用Matveev和Culick论文中提出的涡脱落热声模型对热声振荡进行研究.该热声系统是一两端开口且内部具有后向台阶的管道,管道总长度为L.本研究中采用图中的一维坐标系,Ls为后向台阶的位置,此处有旋涡的生成和脱落,Lc为脱落涡撞击下游壁面的位置.

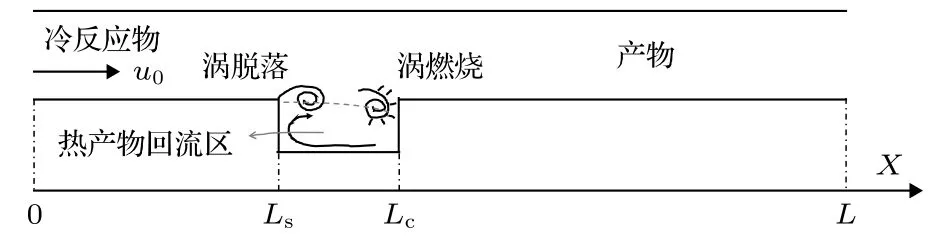
图1 带后向台阶的燃烧室简化模型Fig.1.The simplified model of combustor with backward facing step.

在一定流速 u0下,由于 Ls处剪切层的不稳定性,将有旋涡产生.满足一定条件后,携带着反应物的旋涡从台阶 Ls处脱落,并在凹腔内沿主流与回流区的边界向下游对流,在 Lc处撞击下游壁面并破裂,造成集中燃烧并伴随瞬时热量释放.事实上,在非定常流动中涡的生成、对流、破裂过程的控制方程都是非线性的.为了研究方便,引入Matveev和Culick发展的非定常流中旋涡脱落模型.

2.2 旋涡脱落模型

稳态流动中钝体后将出现有规律的旋涡脱落,涡脱落频率表示为

其中St 为Strouhal数,d 为特征尺寸.由于该热声系统中波动的压力和速度将影响涡脱落过程,Matveev和Culick[18]提出了非定常流中简化涡脱落模型,其中St 与稳态流动下相同,瞬时合速度u (t)=u0+u′(t),台阶后产生的旋涡环量增长率表示为

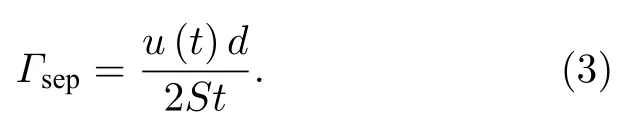
第m 个涡从 Ls处脱落后,向下游运动的速度等于旋涡瞬时位置处的合速度：

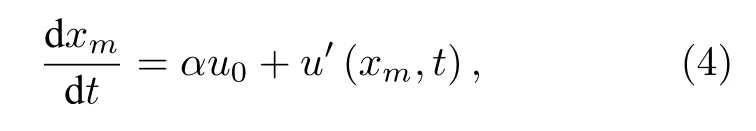
其中 xm为第m 个涡的瞬时位置,u′(xm,t) 为xm处的瞬时脉动速度,α为小于1的系数,通常取0.4—0.6[23].在分段式固体火箭发动机的空腔中,α常取0.5—0.6[26].

2.3 热声模型

忽略温度梯度、黏性效应以及稳态流动对声场的所有直接影响,该系统中声场的动量和能量控制方程可表示为：

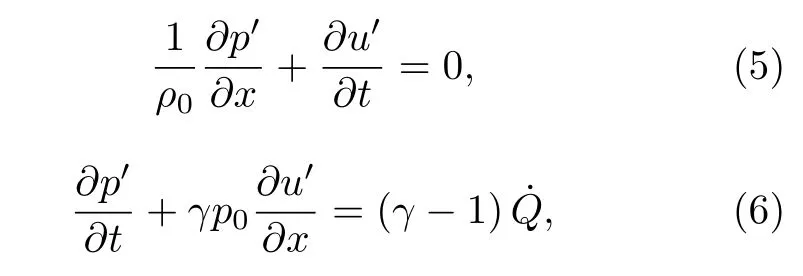
式中 p′和 u′分别为声场的压力和速度波动,γ为比热容比,p0为未扰动的平均压力.为热释放率,可用空间和时间上的delta函数表示为[18]

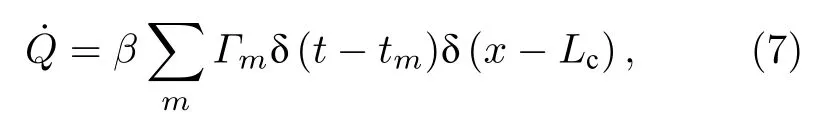
式中的求和可由脱落涡的数量确定,β为一恰当的热释放系数,它将涡撞击与热释放率联系起来,tm为环量为 Γm的第m 个涡的撞击时刻.

采用Galerkin方法将偏微分方程(5)和(6)降阶为一簇常微分方程,为满足两端开口管道的声学边界条件[19],压力和速度波动的Galerkin分解分别为：

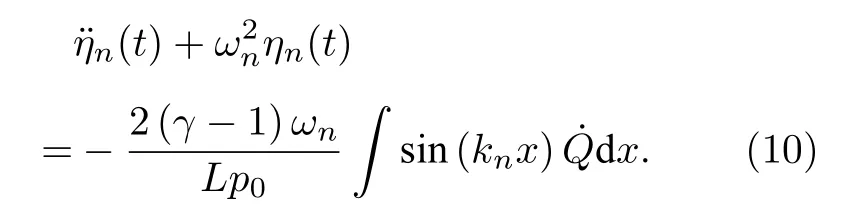
引入阻尼系数 ξn[18]：

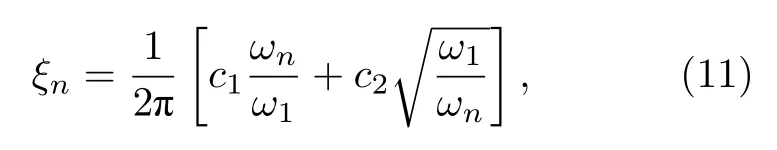
式中 c1和 c2分别为端部损失和边界层损失引起的阻尼系数[9].添加阻尼项并将热源项(7)式代入(10)式可得：

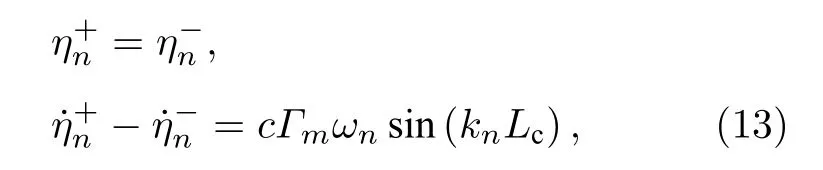
3 计算结果与分析

3.1 计算参数设置与模型验证

本文的计算由编写的MATLAB程序完成,根据已有文献的研究结果及对各种系统参数的试算过程,选择以下参数可以更清晰地呈现该模型的非线性特征：L= 1 m,Ls= 0.3 m,Lc= 0.45 m,α=0.5,γ= 1.4,c0= 750 m/s,c =—0.0015,St /d =10 m—1[19].Matveev和Culick[18]以及Nair和Sujith[21]对模态数进行了讨论,指出取前十阶模态进行研究可满足计算的精度要求和收敛性,因此本文取前十阶模态(N=10)进行计算和分析.当没有脱落涡撞击到 Lc处时(即 t／=tm时),(12)式等号右端为0,采用四阶Runge-Kutta积分计算ηn(t)和(t) ,时间步长 dt 取 10-6s.然后,根据(8)式和(9)式计算出瞬时的压力和速度,再由(2)式和(3)式计算 Ls处的环量及临界环量.如果 Γm≥Γsep,第m 个涡脱落,Ls处的环量重置为0,下一时间步开始计算第(m + 1)个涡的环量.所有的脱落涡在凹腔内以方程(4)的速度向下游运动.当第m 个涡撞击到 Lc处时(即 t =tm时),(t) 以方程(13)发生突跳,而 ηn(t) 不发生变化.在整个计算时间内重复这样的过程,最终可由(8)式和(9)式得到任何时刻和位置的声场压力和速度.文中所有计算结果均取后向台阶处(x =Ls)的时间序列.

为了验证计算模型的准确性,首先将计算参数设置为α= 0.4,c1= 0.0225,c2= 0.0025,u0=50 m/s,其他参数与前文相同,分别在初始扰动η1(0)=0.05和 η1(0)=0.07 下(其他初始扰动均为零 ηn/=1(0)=0,(0)=0)进行计算,与Tulsyan[19]论文中的结果进行对比.图2为计算结果与已有文献的结果对比,数值结果符合较好,左图为η1(0)=0.05时的结果,随时间推移,振荡衰减,右图为 η1(0)=0.07 时的结果,随时间推移,振荡发散.可以看出,初始扰动差异很小,系统的振荡却出现了截然不同的结果.

3.2 系统的初值敏感性

为了进一步分析系统的多解性,将计算参数设置为 c1=0.03375,c2=0.00375[19],u0=50m/s.在两个非常接近的初始扰动 η1(0)=0.01240087 和η1(0)=0.01240088下(其他初始扰动均为零ηn/=1(0)=0,(0)=0),对系统的压力和速度波动进行计算.

取振荡稳定后的 p′/p0时间序列分别进行相空间重构,得到图3(a)和图3(c)所示的压力比的三维相图,其中延迟时间 τ取100.在图3(a)和图3(c)中取 p′/p0(t)=0 的截面,分别得到图3(b)和图3(d)所示的庞加莱截面.其中图3(a)和图3(b)对应η1(0)=0.01240087的计算结果,图3(c)和图3(d)对应 η1(0)=0.01240088 的计算结果.由三维相图和庞加莱截面看出,η1(0)=0.01240087 时,庞加莱截面上呈少量有限个点,说明系统最终趋于小振幅的周期振荡.而对 η1(0)=0.01240088 的初始扰动,取足够长的时间序列,庞加莱截面上没有出现封闭曲线,依然呈现大量有限个点,说明系统最终趋于振幅略大的复杂周期振荡.

图4(a)和图4(b)分别为η1(0)=0.01240087和 η1(0)=0.01240088 下压力比的前0.2 s的时间序列,图中虚竖线为脱落涡撞击并燃烧引起压力突跳的瞬间.可以看出,在两个极为接近的初始扰动下,0.1 s前的时间序列几乎相同,但0.1 s后的时间序列,图4(a)振幅减小,图4(b)振幅增大.初始扰动的微小差异,导致涡脱落的频率及环量大小存在微小差异,差异的积累产生了非线性效应.由于两个初始扰动在不同的吸引域内,系统最终趋于两种不同的解分支,具有典型的非线性特征.

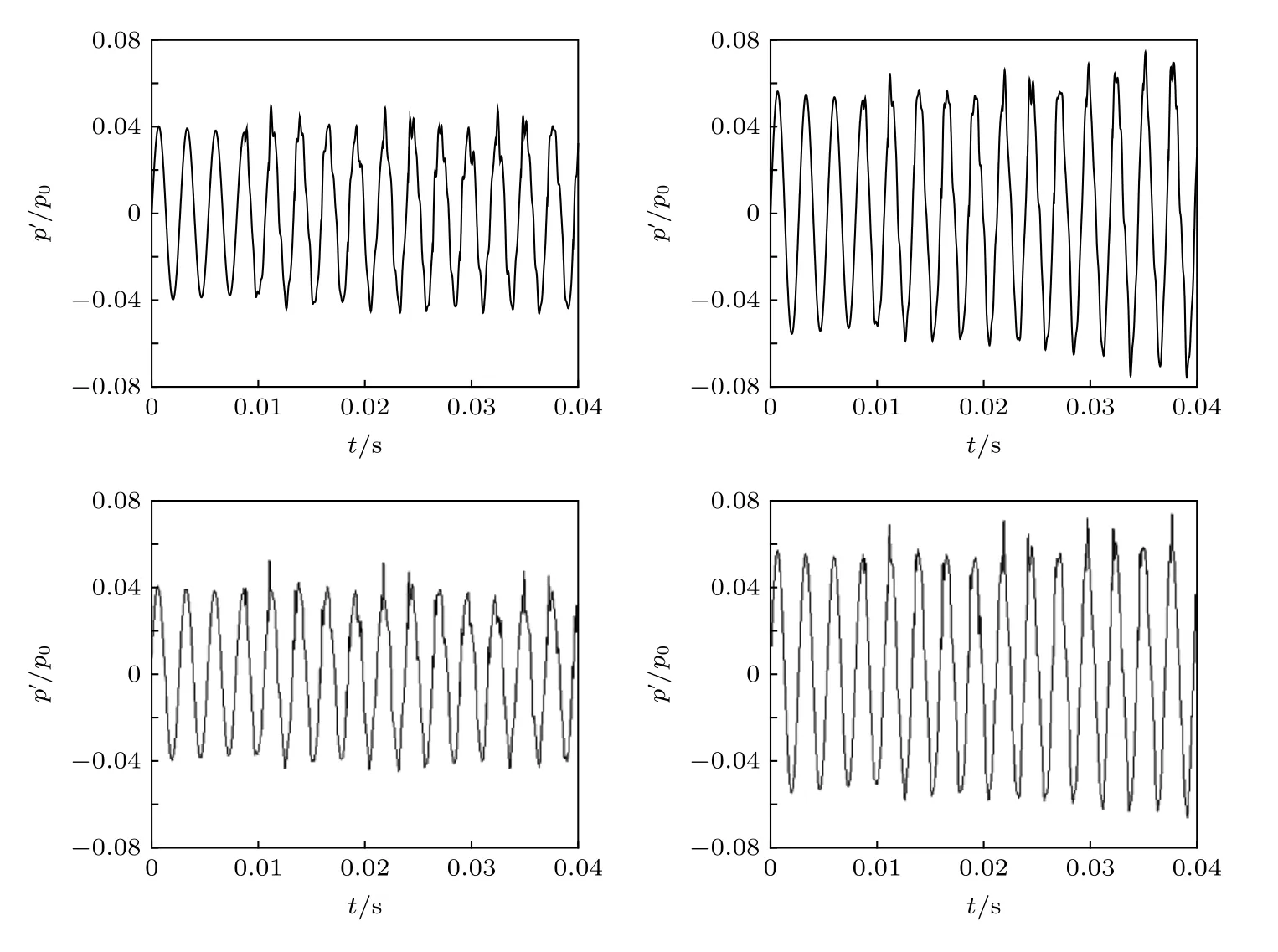
图2 计算模型验证[19]Fig.2.Verification of computation model[19].

图3 相空间重构后的相图及庞加莱截面Fig.3.Phase diagram after phase space reconstruction and Poincaré section.

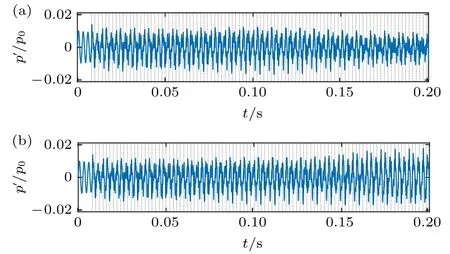
图4 不同初始扰动下压力比的初始时间序列Fig.4.Initial time series of pressure ratios under different initial disturbances.

3.3 压力波动振幅的相似结构

为了研究 u0对系统热声振荡的影响规律,将u0在区间 [5, 100] 内均匀改变,分别计算了381个工况下的 u′,p′.计算过程中阻尼系数c1= 0.135,c2=0.015[9,18],其他参数固定不变,初始条件为零扰动(ηn(0)=(0)=0).在每个工况下 p′的时间序列稳定后,取1.4 s以后的 p′/p0时间序列在每个涡脱落时间间隔内的最大值点和最小值点,得到图5所示结果.

随着 u0增大,稳态涡脱落频率 fs0增大,但压力波动的振幅不一定增大.图5中显示了在不同u0下,压力波动的振幅变化具有相似结构.图6为图5的局部放大图,曲线O1—O2,O2—O3,O3—O4,O4—O5,O5—O6,O6—O7具有相似结构,O1,O2,O3,O4,O5,O6,O7为每一段曲线的峰值点.

图5 不同 u0下的压力比的最大值和最小值Fig.5.Maximum and minimum pressure ratios at different u0.

图7(a)—图7(f)分别为O1—O6的 p′/p0的时间序列,图中虚竖线为脱落涡撞击并燃烧引起压力突跳的瞬间.从图7(a)可以看出,O1点两次涡撞击时间间隔内压力波动经历了7次衰减的周期振荡.从O1—O6工况,两次涡撞击时间间隔内压力波动的周期振荡数目由7次减小到2次.因为随着u0的增大,第一次涡撞击的时刻不断前移,同时涡撞击频率增大,热量释放的频率增大,所以两次涡撞击间隔内的周期数减小.由于速度波动 u′相对于u0很小,Γm主要由 u0主导,随着 u0增大,临界环量 Γsep增大,脱落涡的环量增大,进而由(14)式引起的压力突跳增大.相当于热量释放的强度增大,燃烧过程向声场中加入的能量增大,所以从O1至O6工况下压力振荡的幅值不断增大.同时观察图7(a)—图7(f),六个峰值点处,每次压力突跳(热量释放)均发生在压力振荡的波峰位置,这样使得振荡不断加强.从图7(f)的前几次涡撞击明显看出振荡加强,振幅增大,直到稳定的过程.

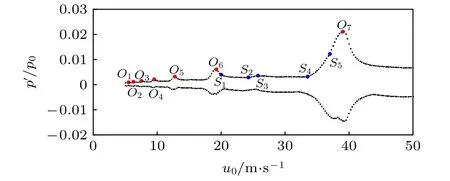
图6 图5的局部放大图Fig.6.Partial enlargement of Fig.5.

为了研究每一段相似曲线上振幅由减小到增大的规律,取O6—O7曲线上S1,S2,S3,S4,S5五个点及O7的 p′/p0的时间序列,得到图8(a)—(f).图8中虚竖线为脱落涡撞击并燃烧引起压力突跳的瞬间,六个工况点的 u0分别为20,24.25,25.75,33.5,37和39 m/s.虽然随着 u0增大,脱落涡的环量增大,热释放强度增大,但是压力波动的振幅却呈现由减小到增大的过程.

优质旅游发展是新时代旅游目的地形象的重要载体。当前旅游规划不仅局限于对景区等旅游目的地的规划建设，对于旅游目的地城市形象以及配套服务设施的规划建设也同样有较高要求。优质旅游发展并不等同于简单的优质旅游服务，它是全域旅游发展到一定阶段的产物，包括优质的旅游治理机制、旅游综合服务、旅游目的地环境等。旅游市场需要高端的规划设计人才，来满足旅游者的更高消费需求。

观察图8(a)—图8(f)中前四次涡撞击的时间序列的放大图,可以看出涡撞击并燃烧放热的瞬间与压力波动之间存在相位差.图8(a)中S1工况下,热量释放(压力突跳)发生在压力振荡的波峰之前,所以相比O6工况振幅减小.随着 u0增大,涡撞击频率增大,热量释放的时刻前移.在图8(b)和图8(c)中,S2和S3工况下热量释放的时刻接近压力振荡的波谷,振荡减弱,所以振幅较小.图8(d)中S4工况下,热量释放发生在压力振荡的波腹,振幅依然较小.图8(e)中S5工况下,热量释放的时刻接近压力振荡的前一个波峰,振荡开始加强,振幅逐渐增大.图8(f)中O7工况下,热量释放发生在压力振荡的前一个波峰处,振荡加强,振幅增大.该变化过程符合Rayleigh准则,即当热量在压力波动的最高点加入或者最低点取出,则振荡加强；反之,振荡减弱.

图7 O1,O2,O3,O4,O5,O6的 p ′/p0时间序列 (a) u0= 5.50；(b) u0= 6.25；(c) u0= 7.50；(d) u0= 9.50；(e) u0= 12.75；(f) u0= 19.25Fig.7.p ′/p0 time series of O1,O2,O3,O4,O5,O6：(a) u0= 5.50；(b) u0= 6.25；(c) u0= 7.50；(d) u0= 9.50；(e) u0= 12.75；(f) u0= 19.25.

随着 u0的增大,压力波动的振幅变化呈现的相似结构将继续下去.u0增大导致涡撞击频率增大,进而热量释放的频率增大,所以两次涡撞击间隔内的压力波动周期数减小,最终将减小到1次,即涡脱落频率与压力波动频率达到1∶1的状态.在每一段相似曲线上振幅由减小到增大,这是由于u0的增大改变了涡撞击并燃烧放热的时刻,热量释放时刻从压力振荡的波峰前移到前一个波谷,再到前一个波峰,热量释放与压力振荡之间的相位差发生了改变.根据Rayleigh准则,相位差的改变导致了压力波动的振幅呈现由减小到增大的相似结构.

3.4 涡声锁频

对3.3节中381个工况下的振荡稳定后的p′/p0时间序列分别做快速Fourier变换(FFT),取FFT变换后最大振幅对应的主频作为压力波动的主频率 fp.根据方程(1)求得稳态涡脱落频率为fs0,实际的涡脱落频率为 fs,由频率比 fs0/fp和fs/fp可得图9所示结果.

由图9可以看出,压力波动的主频 fp与涡脱落频率 fs之间存在锁频关系,形成图中所示的三角形锁频区域.图9中从右上角到左下角呈现8个台阶,fs/fp依次为1,1/2,1/3,1/4,1/5,1/6,1/7,1/8.该锁频现象称之为涡声锁频,其可以作为周期性燃烧振荡出现的重要标志.该涡声锁频现象的出现本质上是由于发生了稳定的自激振荡：热声振荡现象是不稳定热释放率与燃烧室内声场波动相互作用的过程,燃烧振荡稳定后,涡脱落并撞击燃烧导致的热量释放与声场的压力、速度波动之间构成了可以自持的正反馈回路,形成了稳定的自激振荡.计算模型中不稳定热释放由涡脱落导致,所以涡脱落频率是影响该热声振荡过程的关键因素.随着 u0变化,涡脱落频率改变,进而热量释放频率改变,当热量释放与压力波动之间发生稳定自激振荡,稳定的热声振荡出现,同时涡脱落频率与压力波动频率呈现锁频现象.图10为 fp与 fs的关系及fs/fp随 u0的变化图.由图10可以看出,随着 u0增大,涡脱落频率 fs增大,压力波动的主频率 fp向高频发展,同时 fs/fp接近1.u0增大导致涡脱落频率增大,进而热释放频率增大,由3.3节的分析可以发现,两次涡撞击间隔内的压力波动周期数最终将减小到1,所以涡声锁频的频率比最终趋于1,这也与3.3节的解释一致.

图8 S1,S2,S3,S4,S5,O7的 p ′/p0时间序列Fig.8.p ′/p0 time series of S1,S2,S3,S4,S5,O7.

图9 涡声锁频Fig.9.Vortex-acoustic frequency locking.

图11为图7中O1,O2,O3,O4,O5,O6六个不同工况下的 u′-p′/p0相图.相图中的短竖线显示了脱落涡撞击并燃烧放热的瞬间,压力发生突跳,而速度不变.图11(a)—图11(f)中 fs/fp分别近似等于1/7,1/6,1/5,1/4,1/3,1/2,相应的u′-p′/p0相图中相轨迹旋转了7,6,5,4,3,2圈.该现象与图7一致,从图7(a)—图7(f)每经过一次涡撞击并燃烧放热,阻尼振子(压力波动)分别经历7,6,5,4,3,2次周期振荡.系统的振荡稳定后,阻尼振子受到周期性涡撞击燃烧放热这一强迫作用,系统近似可以看作两个振子的耦合.此时可以将系统当作离散系统,用离散映射处理.两振子耦合时,它们在三维相空间的轨迹将限于一个二维环面上.相角和频率是决定耦合振子运动性质的关键因素,所以在环面上选取适当的庞加莱截面,只考虑圆周上的庞加莱映射,即圆映射.在二维环面上当第二振子转动一周时,第一振子转动的圈数为第一振子与第二振子频率之比.在该热声振荡系统中,两次涡撞击时间间隔内阻尼振子的周期振荡数目即为二维环面上周期的强迫振子(涡撞击)转动一周,阻尼振子转动的圈数.该圈数即为压力波动的主频率fp与涡脱落频率 fs的比值 fp/fs.该比值也与图11中相轨迹旋转的圈数一致.同时,该比值为整数,所以在所选的庞加莱截面上映射结果不变,系统的热声振荡就是以周期强迫振子(涡撞击)的频率(fs)的整数(fp/fs)倍做周期振荡,即转数为fp/fs的锁频(又称锁相或锁模).

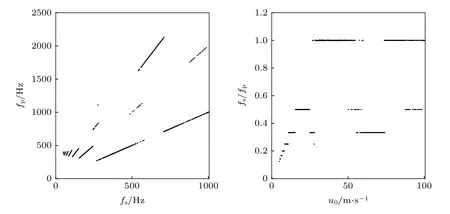
图10 f p 与 f s 的关系及 f p/f s 随 u 0 的变化图Fig.10.The relationship between fp and fs and the change of fp/fs with u0.

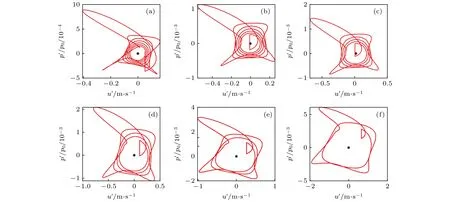
图11 6个不同频率比下的 u ′-p ′/p0相图 (a) fs/fp= 0.1430；(b) fs/fp= 0.1669；(c) fs/fp= 0.2003；(d) fs/fp= 0.2500；(e) fs/fp=0.3330；(f) fs/fp= 0.4999Fig.11.u ′-p ′/p0 phase diagram at six different frequency ratios：(a) fs/fp= 0.1430；(b) fs/fp= 0.1669；(c) fs/fp= 0.2003；(d) fs/fp=0.2500；(e) fs/fp= 0.3330；(f) fs/fp= 0.4999.

4 结 论

基于Matveev和Culick提出的涡脱落热声模型,引入旋涡脱落模型,建立系统热声振荡的控制方程,采用Galerkin方法将控制方程转化为常微分方程并进行数值求解,得到了声场的压力和速度波动,分析了稳态流动速度 u0对热声振荡的影响,同时对出现的涡声锁频行为进行了研究,得到如下结论.

1)该涡脱落热声振荡系统对初值极为敏感,是典型的非线性动力系统.初始扰动的微小差异,导致了不同的非线性效应,系统呈现多解性.

2)随着 u0增大,稳态涡脱落频率 fs0增大,但压力波动的振幅不一定持续增大,而是具有相似结构.随 u0增大,脱落涡的环量增大,热量释放强度增大,压力波动的振幅总体呈增大趋势,但在 u0的每个小区间内振幅又重复出现先减小后增大的相似结构.涡撞击并燃烧放热的瞬间与压力波动之间存在的相位差影响着振幅变化,在振幅极大值点,涡撞击并燃烧放热发生在压力振荡的波峰处,振荡加强,符合Rayleigh准则.

3)该模型在不同 u0下的热声振荡过程均呈现了涡声锁频现象.系统最终的热声振荡就是以涡撞击的频率(fs)的整数(fp/fs)倍做周期振荡,即呈现转数为 fp/fs的锁频.文中所研究的工况形成了fs/fp依次为1,1/2,1/3,1/4,1/5,1/6,1/7,1/8的三角形涡声锁频区.该涡声锁频现象可以作为周期性燃烧振荡的重要特征.

虽然本文对涡脱落引起的热声振荡中相似性和涡声锁频这两种典型非线性现象进行了研究,发现了主流平均流速改变下压力波动振幅呈现的相似结构,以及解释了热声振荡实验中出现的涡声锁频的形成机理,但是对该热声振荡中存在的其他复杂非线性现象并未涉及,特别是实验中出现的迟滞、分岔等非线性行为,这将是下一步的研究工作.