基于CFD的旋风分离器短路流计算方法分析

摘要：为了研究短路流计算方法，借助STAR-CCM+软件对旋风分离器内部流场进行了模拟分析，发现排气管外沿正下方存在一个轴向速度零点，该点至排气管下端之间流过的气流较为接近真实的短路流，并基于这个轴向速度零点提出了一个旋风分离器短路流计算方法。

关键词：旋风分离器;短路流;CFD

中图分类号：TQ051.8 文献标识码：A 文章编号：1007-9416（2019）09-0056-02

0 引言

旋风分离器短路流是指由旋风分离器顶板附近的二次流现象引起的，一股沿着排气管外壁向下流动，并最终流入排气管口的气流。这股气流是从旋风分离进气口流入旋风分离器后，并未经过旋风分离器的分离区进行气、固或者气、液分离，直接从旋风分离器上部流入排气管口，因此这股气流会直接携带其中的颗粒或者液滴进入排气管，其大小对旋风分离器的分离性能有重要影响。由于短路流与其它气流同处一个流动空间，气流速度大，流态处于湍流状态，且存在涡旋流动，因此短路流与其它气流没有明显的边界，要想精确计算短路流非常困难。本文借助计算流体力学（CFD）软件STAR-CCM+对旋风分离器内部的流场进行模拟分析，并在分析基础上建立旋风分离器短路流计算方法。

1 三维模型及网格

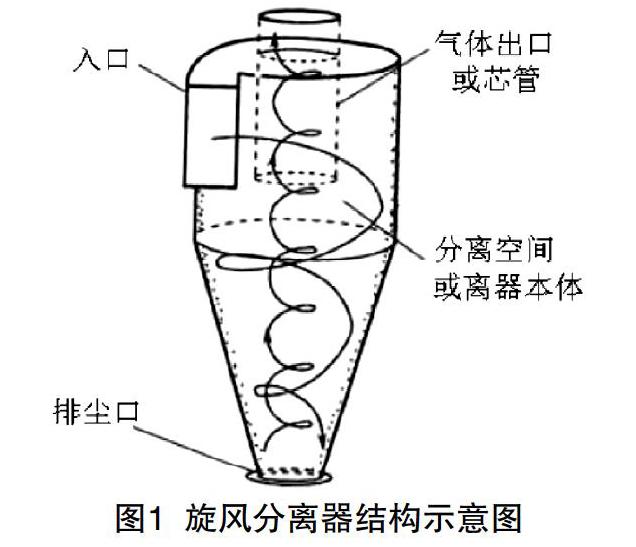
本文研究的旋风分离器为逆流式筒椎型结构，其结构示意图[1]如图1所示。携带固体颗粒或者液滴的气体从旋风分离器入口进气，主流气体沿着壁面旋流转向下流动，同时流向旋风分离器的中心，旋风分离器中心则从底部逐渐形成一股逆向旋转并向上流动的气流，向上旋流过程中逐渐汇集外侧流向中心的气流，最终从排气管排出。

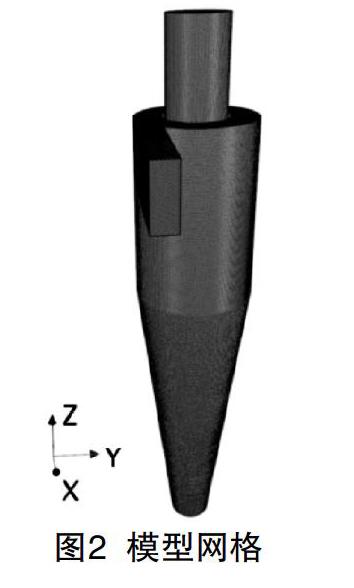
模拟计算的旋风分离器各尺寸参照相关文献[2]，为提高计算效率，采用多面体网格，生成网格如图2所示，并进行网格无关性验证。

2 计算模型和条件

相关研究已表明[3，4]，旋风分离器内部有较强的旋转运动，湍流模型选用RSM模型比较适合。由于这里只针对短路流进行计算，因此可以不考虑离散相的模型选择和相应参数设置，其它具体边界条件和参数的输入参照参考文献[2]设置，这里不再赘述。

3 短路流计算方法

3.1 计算依据

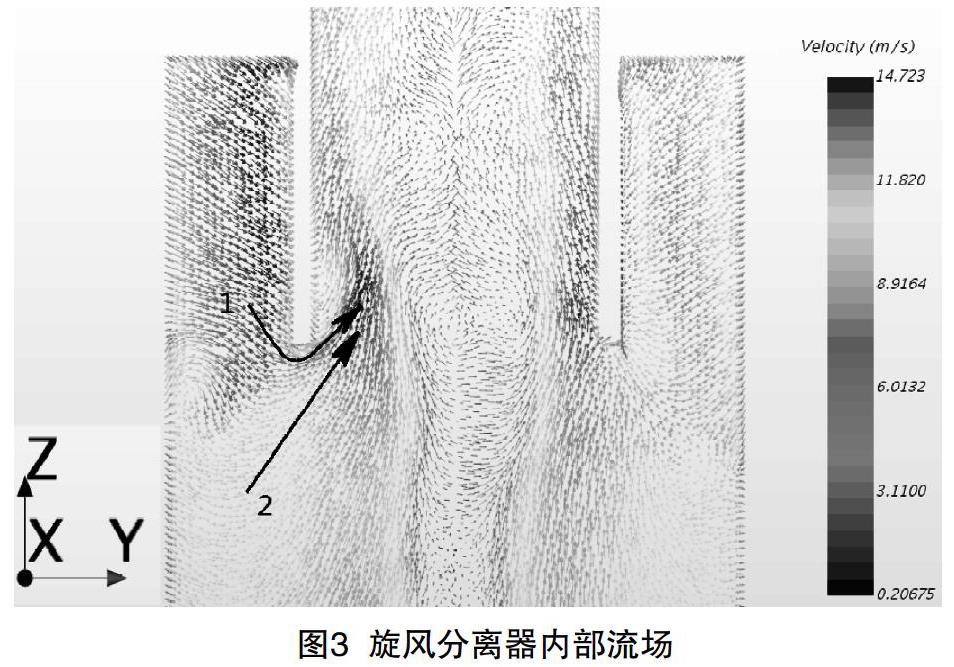
旋风分离器内部流场图3所示，图中排气管口附近的外侧有两股气流流入管口，分别标注为气流1、气流2。其中气流1为从排气管口上方流下并流入排气管口的气流，通过流场分析追溯其来源，可以发现这股气流来自旋风分离器进口，并沿着顶板回流或直接向内侧流入排气管口，这股气流未经过分离空间进行气固或者气液分离，因此这股气流可以认为是短路流。而气流2来自排气管下方的分离空间，是已经过气固或者气液分离的气流。

由于这两股气流在同一空间内流动且未严格分层，要计算出完全真实的短路流，几乎不可能实现。但是放大排气管口下方的区域见图4所示，可以看出，向下和向上流动的气流相互冲击，流向逐渐改变，并在排气管口外沿正下方某个位置（图4中打叉的位置）流向变为水平相切，轴向速度变为零。因此可以定义排气管外沿正下方轴向速度等于零的位置为上下流动两股气流的分界点，分界点以上流入排气管的气流为短路流。虽然分界点以上流入排气管的气流并不是真实的短路流，但是通过上述分析可以看出该气流已比较接近真实的短路流，并且该分界点在流场中可以精确计算得出。

3.2 具体计算方法

根据上述原理，计算旋风分离器短路流需找出排气管口外沿正下方的上下流动两股气流分界点（后面简称分界点），然后根据上下气流分界点设置环形柱面，最后计算流过环形柱面的气流量大小，下面依次展开说明。

（1）需要找出排气管口外沿正下方上下两股气流的分界点，即排气管口外沿正下方第一个轴向速度等于零的位置。之所以强调“第一个”，是因为在排气管外沿正下方存在多个轴向速度等于零的点，但经过流场对比，发现只有离排气管下端最近的那个轴向速度等于0的位置对应的才是分界点。因此在排气管外沿正下方设置一系列监测点，用以监测轴向速度，如图5所示，为提高计算精度，可适当加密监测点数量。

设置完监测点后，将这些监测点的轴向速度值导出，在表格数据中找到第一次穿越零轴向速度线的对应两个Z轴坐标数值，对这两个Z轴坐标值关于零轴线速度线插值，得出零轴线速度对应的Z轴坐标值，该坐标轴值与排气管下端的Z轴坐标的差值的绝对值便是分界点与排气管下端的距离。为消除气流不对称对计算结果的影响，可以在排气管外沿下方周向均匀布置多列监测点，并用上述方法找出各列监测点的分界点，并对它们的轴向位置进行几何平均。

（2）设置短路流所流过的环形柱面。由于在软件中暂时设置不了一段柱面，只能设置整个计算区域的柱面，因此这里以旋风分离器轴心为柱面中心，以排气管外径为直径，作一个柱面。由于短路流是流过排气管下端到分界点之间这一段柱面的气流，若直接用流量函数与前面所作的柱面做积分，则所计算出来的结果是错误的。为解决这个问题，可以通过定义函数的形式，强制定义排气管下端到分界点之间以外的区域流量函数为0。如本文所设置的函数形式为“[$Density*$$Velocity[0]*（$$Position[2]>-0.00173？1：0），$Density*$$Velocity[1]*（$$Position[2]>-0.00173？1：0），0]”，其中“-0.00173”即分界点的Z轴坐标。

（3）设置面积分运算，积分曲面选择所定义的柱面，积分函数选择自定义的流量函数，设置完成之后运算面积分即可计算出短路流大小。

4 结语

本文采用CFD技术，对旋风分离器的短路流计算方法进行了研究，发现旋风分离器排气管外沿下方存在一个轴向速度零点，该点至排气管下端之间的气流较为接近真实的短路流，在此基础上提出了一个基于CFD计算短路流的计算方法，并详细阐述了借助STAR-CCM+实现该方法的具体步骤。

参考文献

[1] 霍夫曼（Alex C. Hoffmann），斯坦因（Louis E. Stein）著.旋风分离器——原理、设计和工程应用[M].彭维明，姬忠礼，译.化学工业出版社，2004.

[2] 满林香.基于STAR-CCM+的旋风分离器数值模拟方法的研究[J].大众科技，2019（6）：59-61.

[3] 魏新利，张海红，王定标.旋风分离器流场的数值计算方法研究[J].郑州大学学报（工学版），2005（1）：57-60.

[4] 金向红，金有海，王建軍，等.改进气液旋流器排气管结构的实验及CFD模拟研究[J].高校化学工程学报，2011（02）：205-211.

Abstract：In order to study the short-circuit flow calculation method， the internal flow field of the cyclone separator was simulated and analyzed by STAR-CCM+ software， it is found that there is an axial velocity zero point directly below the outer edge of the exhaust pipe， the airflow flowing between the point to the lower end of the exhaust pipe is closer to the true short-circuit flow， and based on this a method of calculating the short-circuit flow of cyclone separator is proposed.

Key words：cyclone separator; short circuit flow; CFD