AA2050合金蠕变时效本构方程的改进

张显飞，赵忠兴

(沈阳理工大学 材料科学与工程学院，沈阳 110159)

航空航天工业对构件的综合性能要求越来越高，如对铝合金构件要求具有高的强度和刚度，抗疲劳断裂能力好，耐应力腐蚀性能高等。蠕变时效成形技术是利用金属的蠕变特性，将成形与时效同步进行的一种成形方法。对可时效强化型合金，可应用蠕变时效成形技术生产具有复杂外形和结构的构件，可提高合金材料强度和刚度、提高抗疲劳断裂的能力等；与常规的塑性成形方法相比，成形应力低于屈服应力，降低了材料发生破裂的几率。同时，时效成形过程中由于蠕变而导致应力松弛及后续回弹，使时效成形铝合金结构件残余应力水平低、耐疲劳与应力腐蚀性能提高、长期服役能力更好。因此蠕变时效成形技术在航天航空工业中得到广泛应用[1-5]。

蠕变时效成形过程分为3个阶段：加载过程、时效(蠕变、应力松弛)和卸载阶段[6]。其中蠕变由初始、稳态和加速蠕变阶段组成[7]。从蠕变时效成形过程可以看出，由于受到材料本身时效周期的限制，无法将构件内已有的弹性变形全部转变为塑性变形，因此当外部载荷去除后，成形的构件均会产生一定量的回弹；所以，应用蠕变时效成形技术要获得高精度的工件，通常在确定模具型面时需把回弹量考虑进去，通过补偿的方法消除回弹的影响。早期研究者主要是采用“试错法”，即通过大量的基础工艺试验及经验公式的外推来完成对模具型面的设计，这种方法效率不高，而且适应性较差。随着数值计算技术的发展，数值模拟被大量应用于研究蠕变时效成形过程及模具型面补偿的计算[8-12]。其中有限元方法可以计算构件蠕变时效过程、预测构件回弹[8-10]。有限元法模拟蠕变时效成形过程的一个关键问题是建立描述材料蠕变时效成形过程的本构方程。

最常用于预测合金稳态蠕变应变的是幂函数方程[13-14]、扩展的幂函数方程、双曲函数方程以及Orowan方程。随着对材料微观组织测试手段的完善及对合金蠕变机理研究的深入，将微观组织对合金蠕变过程的影响考虑进模型里[15]。文献[16-18]基于蠕变、应力松弛理论和时效动力学，提出了将应力应变分析与微观组织演化(如沉淀相析出、析出相溶解、晶粒长大、位错、溶质密度等)相结合的统一的蠕变时效本构方程。引入蠕变变量H，将蠕变速率表示为应力、位错强化和时效强化的函数；同时，沉淀相的形核、长大，溶质浓度的变化均与蠕变变形量相关。基于此本构方程并结合ABAQUS有限元软件，对AA2050铝合金蠕变时效过程进行模拟。然而在应用文献[18]给出的本构方程模拟AA2050合金蠕变时效时发现，其H值计算出现了H>1的情况，造成蠕变速率计算结果产生突变，使蠕变应变计算结果不准确。据此，本文改进了文献[18]提出的本构方程参数的计算方法，基于ABAQUS软件，模拟了AA2050合金蠕变时效成形过程。

1 蠕变时效成形本构方程的改进

(1)

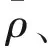
(2)

式中：k1～k3为加权系数，取值0～1；β为新析出相半径与溶解半径的权重系数。

根据文献[19]可知AA2050-T34温度为155℃、150MPa拉应力下蠕变速率随时间变化的结果，应用式(1)及文献[18]给出的参数，可计算出H值与时间的关系，见图1所示。

图1 H值与时间的关系曲线

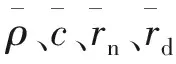
i=1,2,3

(3)

文献[18]给出的本构方程式(1)中，B1为常数；然而，在应用中发现B1为常数时，式(1)并不能适应不同应力下的蠕变速率计算。因此，根据文献[19]给出的实验结果，本文将B1取为应力σ的函数。

B1=0.082exp(-0.00159σ)

(4)

位错密度变化速率为

(5)

新析出相半径变化率为

(6)

考虑析出相溶解，其半径变化速率为

(7)

溶质浓度变化速率为

(8)

屈服强度σy为位错强化项、固溶强化项及析出强化项的函数。

(9)

位错强化速率为

(10)

固溶强化速率为

(11)

析出相溶解强化速率为

(12)

析出强化速率为

(13)

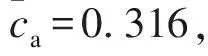
2 本构方程验证

模拟计算了AA2050-T34，温度为155℃、150MPa拉应力作用下蠕变时效过程。采用的试样尺寸见图2所示[19]。

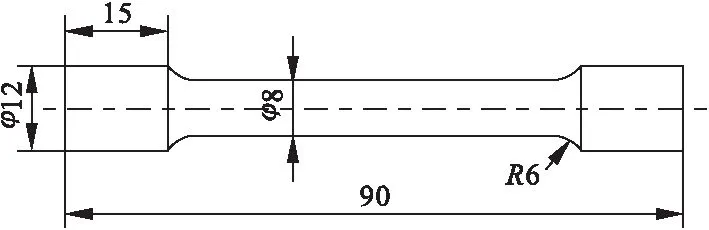
图2 蠕变试样尺寸

计算用到的变量初始值见表1。基于文献[19]的实验数据，对本构方程参数进行拟合，结果见表2所示。

表1 计算用到的变量初始值[18]

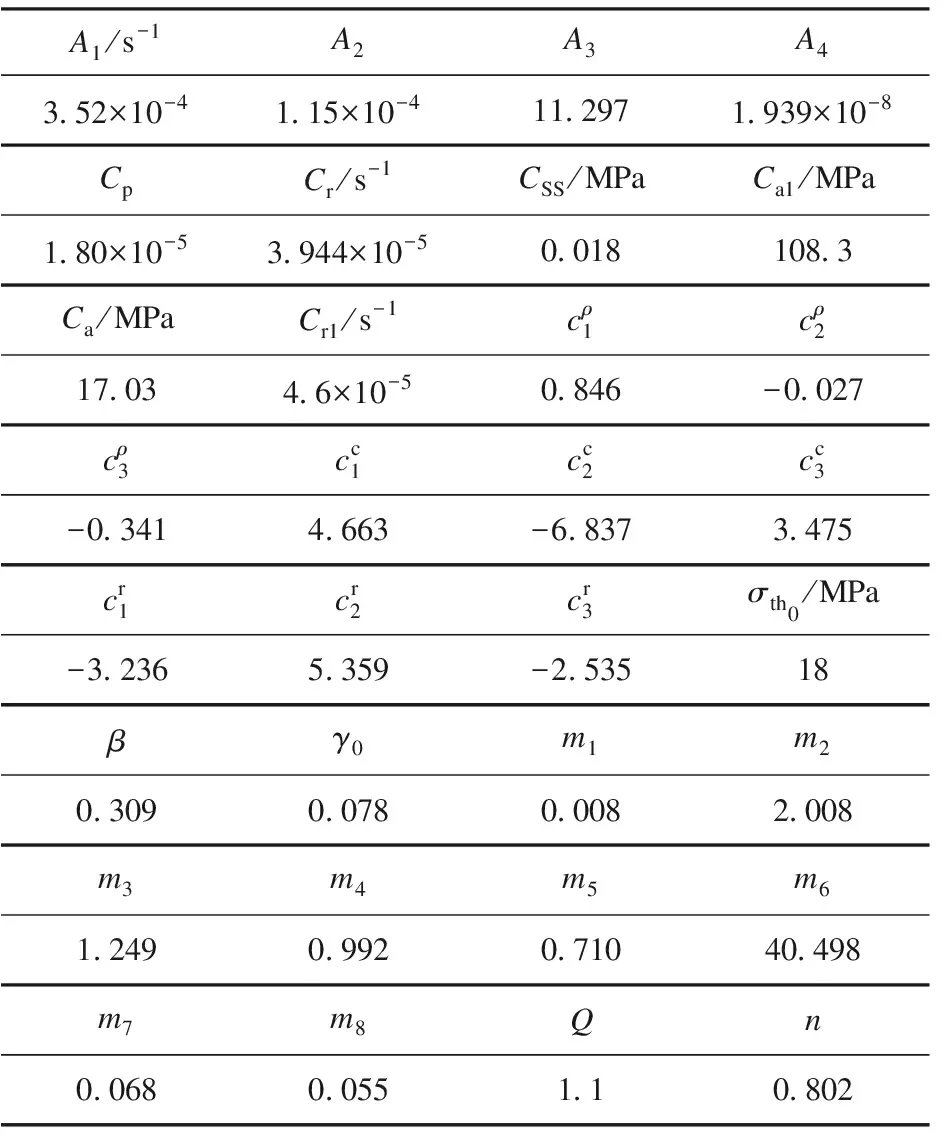
表2 本构方程参数

2.1 蠕变速率及蠕变应变

模拟计算150MPa拉应力下，AA2050-T34合金蠕变时效过程。

根据文献[19]蠕变应变速率的实验数据，由式(1)可反推出H值与时间的关系，见图3所示。由式(2)计算获得的H值如图3中实线所示。可见，拟合的H值与由文献[19]实验结果反推出的H值吻合良好。

图3 值与时间的关系

AA2050-T34，155℃、150MPa拉应力下计算得到的蠕变速率见图4所示。图4中也给出了文献[19]的实验结果。

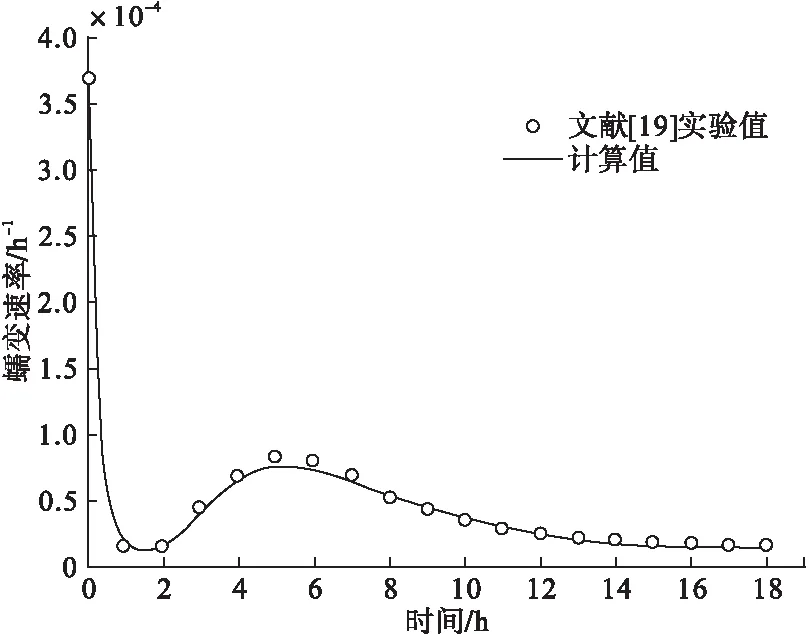
图4 蠕变速率随时间的变化曲线

从图4可知，在蠕变时效的各个阶段，本文模拟结果与实验结果都高度吻合。蠕变速率计算决定了蠕变应变的计算结果的准确性。图5为应力100MPa、150MPa、175MPa，AA2050-T34蠕变应变随时间的变化。

由图5可见，蠕变过程与实验结果吻合很好。文献[19]将AA2050-T34蠕变时效过程分为五个阶段：初始瞬时蠕变阶段、瞬时稳定阶段、反向阶段、第二蠕变阶段、第二稳定阶段。模拟结果很好的显示了这一蠕变特征。图5显示，本文计算结果优于文献[18]的计算结果。

1.瞬时蠕变阶段；2.瞬时稳定阶段；3.反向阶段；4.第二瞬时蠕变阶段；5.第二稳定蠕变阶段

图5 蠕变应变随时间的变化

2.2 微观组织

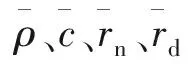
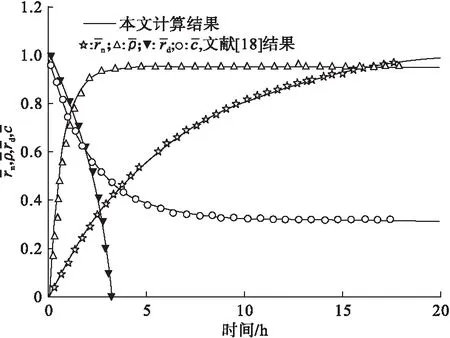
图6 本文计算值与文献[18]计算值的比较

由图6可见，本文计算结果与文献[18]的计算结果吻合很好。由图5和图6的结果发现，虽然本文计算得到的蠕变应变与文献[18]的计算结果不同，但本文计算微观组织与文献[18]的结果相吻合，可见蠕变应变计算结果对微观组织计算结果几乎没有影响。

2.3 时效硬化

图7为AA2050-T34蠕变时效过程中屈服强度随时间的变化。

图7 强度与时间的关系曲线

由图7可见，本文计算得到的σy与文献[19]的实验结果吻合良好。图7中同时给出了本文的σss、σdis、σp-n、σp-d的计算值以及文献[18]的计算结果。可见本文计算结果与文献[18]的计算结果吻合。

由以上分析可见，改进后的本构方程可用于研究AA2050-T34蠕变时效行为，结果更可靠。

3 结论

改进了AA2050-T34蠕变时效行为本构方程，采用新的计算方法计算本构方程中与微观组织相关项系数H、B1；模拟计算了AA2050-T34蠕变时效行为。计算获得的H值均小于1，避免了本构方程参数计算对模拟结果的影响。计算得到的AA2050-T34在温度为155℃、150MPa拉应力作用下蠕变时效微观组织变化与文献[18]结果相符，计算得到的屈服强度与文献[19]的实验结果吻合很好。改进后的本构方程可用于研究AA2050-T34蠕变时效行为。