基于复杂网络动力学模型的链路预测方法

潘永昊，于洪涛，吴翼腾

基于复杂网络动力学模型的链路预测方法

潘永昊，于洪涛，吴翼腾

（国家数字交换系统工程技术研究中心，河南 郑州 450002）

链路预测是复杂网络中研究缺失连边和未来形成连边的重要组成部分，当前基于网络结构的链路预测方法成果丰富，而基于复杂网络动力学模型的链路预测研究较少。针对无权无向网络，首先构建了复杂网络动力学模型，然后给出了基于复杂网络动力学模型的链路预测节点中心性的量化评价指标，最后通过给出的节点中心性量化指标，提出了由复杂网络动力学模型定义的链路预测方法。通过在真实网络数据集上进行的实验表明，提出的链路预测方法较基准方法有明显的预测精度的提升。

复杂网络；链路预测；网络动力学

1 引言

链路预测（link prediction）[1]是复杂网络研究中的一个重要内容，主要研究网络中缺失信息的补全和网络结构的演化，具体为对网络中缺失连接、未来形成连接的预测。链路预测研究在很多领域得到了广泛的应用，如生物蛋白质结构构建[2]、社会网络结构分析[3]、网络演化机制[4-5]等。

现有的链路预测方法主要基于网络拓扑结构，如基于共同邻居[6]相似性的方法、基于路径[7]相似性的方法、层次结构模型[8]和随机分块模型[1]等。近年来，新出现的研究大多是基于网络拓扑结构的方法[9-13]。在基于网络拓扑结构的研究中，一个重要的依据是基于度中心性节点重要性评价，即对于网络中的节点，度越大，其在网络中的重要性和影响力越大。目前，大量的链路预测方法中使用了基于度中心性的节点重要性评价[14]，如在基于共同邻居相似性的链路预测中，Adamic-Adar指标[15]、大度节点不利指标[16]（HDI，hub depressed index）等相似性指标认为，度小的共同邻居节点的贡献大于度大的共同邻居节点。基于度中心性的节点重要性评价方法在链路预测的应用中具有方便直观、运算复杂度低的特点，并且具有很好的预测精度。然而，基于度中心性的节点重要性评价方法以节点的局部特征为计算标准，仅能表示出该节点的局部连边关系，不能充分反映该节点的重要性和影响力。而在实际的链路预测中，不同的网络在结构特征上各有差别，预测精度的高低与链路预测方法中的结构特征有直接的关系。现有的研究成果大多使用节点度作为节点重要性的评价方法，因此，考虑采用另外一种角度对节点度进行调整，研究链路预测问题。

相关研究表明，在考虑网络拓扑结构的同时，对节点的动力学行为进行建模，所得到的复杂网络动力学模型能够更加深刻地揭示网络结构与节点之间的本质关系和规律。Liu等[17]的研究中发现网络中节点动力学模型相同的复杂网络动力学系统中，驱动节点倾向于避免大度节点，这与文献[15]中认为的共同邻居节点中小度节点的贡献大于大度节点异曲同工，但却更深刻地反映出网络中的动力学规律。Jia等[18]的研究表明，网络中节点是否为驱动节点，与节点的入度有关，与出度无关。在孔江涛等[19]的研究中提出了基于复杂网络动力学模型的节点重要性评价方法，通过对节点引入一个驱动因素，计算网络再次达到稳定状态以后所有节点的偏移量，偏移量大的即为重要节点。可以看出，基于网络动力学模型的研究，包含了网络拓扑结构、节点动力学建模，能够具体描述分析时域上网络状态的变化，得到的结果优于只基于网络拓扑结构的研究。

针对以上分析，本文考虑使用复杂网络动力学模型的研究方法，对无权无向网络进行节点动力学建模，引入文献[19]中的扰动测试方法对节点重要性进行量化评价，对现有的基于度中心性的链路预测方法进行改进，提出基于复杂网络动力学模型的链路预测方法。最后通过在真实网络数据集上的实验，证明本文提出的方法能够有效提高链路预测的精度。文章创新点如下：1) 考虑使用复杂网络动力学模型对静态无权无向网络模型进行扩展，对网络节点进行动力学建模，在复杂网络动力学模型上研究链路预测问题；2) 提出了基于复杂网络动力学模型的链路预测方法，并在真实网络数据集上验证其有效性。

2 相关工作

链路预测问题自提出以来，经过多年的研究，已经形成了丰富的研究成果，本节给出几种典型的基于度中心性的链路预测相似性指标的定义。

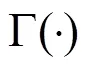
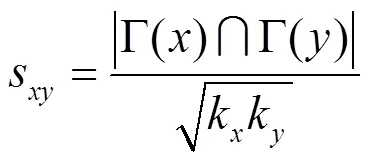
Sørenson指标[1]由Sørenson提出，基于节点的共同邻居集合定义，常用于研究生态学数据，定义式如下。

大度节点有利指标（HPI，hub promoted index）[16]被用于刻画新陈代谢网络中反应物的相似程度，认为度大的节点在网络中与其他节点具有更大的相似性，定义式如下。

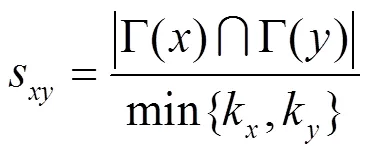
大度节点不利指标（HDI，hub depressed index）[21]认为度小的节点在网络中与其他节点具有更大的相似性，定义式如下。

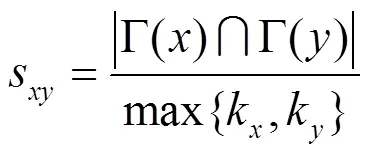
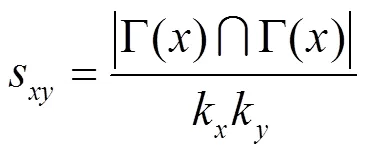
Adamic-Adar指标[23]认为网络中度小的共同邻居节点的贡献大于度大的共同邻居节点，定义式如下。

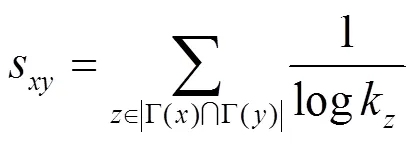
资源分配指标（RA，resource allocation）[21]与AA指标相似，采用与AA指标不同的归一化方法，定义式如下。

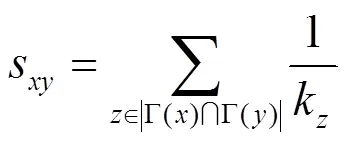
3 问题描述

链路预测相似性计算指标的定义包含对节点在网络中重要性的评价。一种能够充分契合实际网络中节点重要性的评价方法，使相似性指标更加契合当前网络的真实情况，得到更好的预测精确度。

4 主要内容

复杂网络动力学模型同时考虑网络拓扑结构和节点动态属性，能够反映出网络的本质特征。本节首先定义复杂网络动力学模型，然后给出复杂网络动力学模型的节点重要性评价方法[19]，最后定义改进的链路预测相似性指标。

4.1 复杂网络动力学模型定义

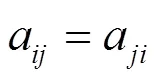
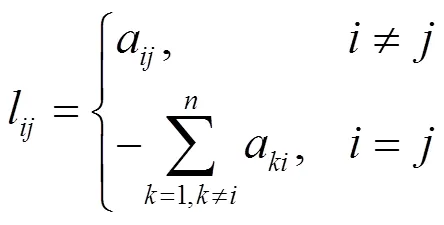
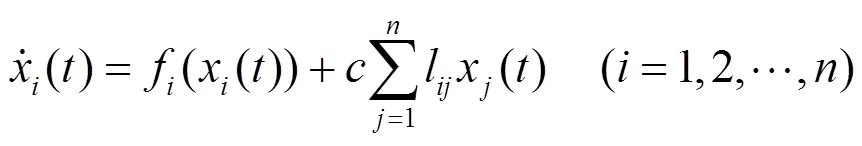
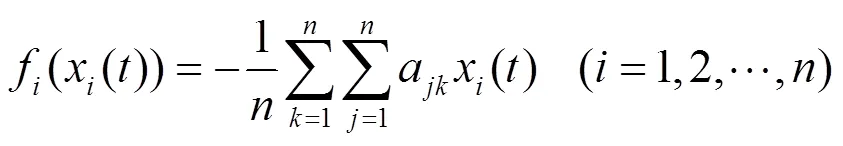
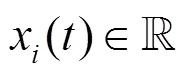
4.2 节点重要性评价指标

式(10)和式(11)定义了复杂网络动力学模型，下面给出基于扰动测试[19]的节点重要性评价指标。

考虑当单个节点发生变化时，对整个网络平衡状态的影响，通过计算影响程度，得到节点的重要性量化评价指标，基于网络动力学模型定义的节点重要性指标[19]，能够很好地反映出节点在网络中的重要程度和影响力。

设动态系统的状态方程为

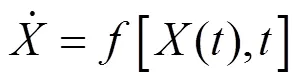
设无权无向网络的动力学模型的状态方程为

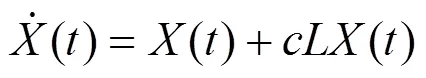
扰动模型定义如下。

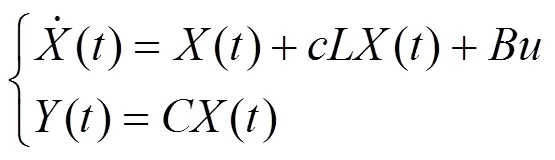
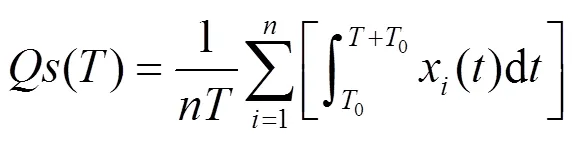
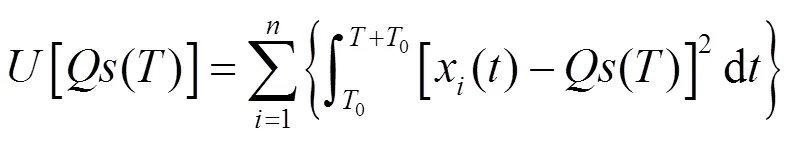
使用基于偏离均值的方差定义节点的重要性指标，其数值越大，节点在网络中的重要性和影响力越大，反之则小。

4.3 链路预测模型

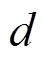
基于复杂网络动力学模型的Salton指标为

基于复杂网络动力学模型的Sørenson指标为

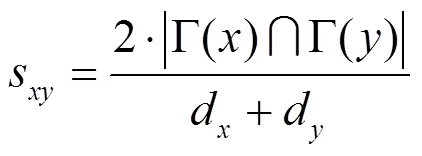
大度节点有利指标是针对节点的度设计计算的，为了便于理解，把基于偏离均值的方差重新定义指标记为基于复杂网络动力学模型的大度节点有利指标。

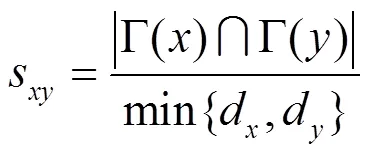
同样，对于大度节点不利指标，把基于偏离均值的方差重新定义指标记为基于复杂网络动力学模型的大度节点不利指标。

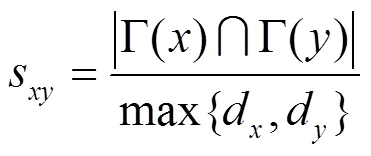
基于复杂网络动力学模型的LHN-I指标为

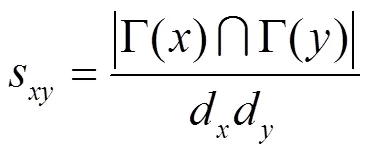
基于复杂网络动力学模型的Adamic-Adar指标为

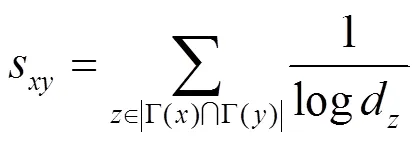
基于复杂网络动力学模型的资源分配指标为

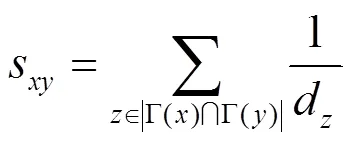
以上给出的指标是在原始指标的基础上对节点度进行了修改，出发点是考虑节点的度在各个原始指标中的意义，实际上，网络本身就是表示当前节点在网络中的重要性和影响力。需要说明的是，对于一些改进后的指标，如余弦相似性、大度节点有利、大度节点不利等，其定义与原始指标的定义初衷发生了一些变化，但修改部分所表达的意义是相同的。

5 实验分析

5.1 实验数据集

为了验证上文中给出的链路预测算法的有效性，本文在4个真实网络数据集上进行链路预测对比实验，分别为：

1) 爵士音乐家合作网（Jazz）[25]，网络中的节点为爵士音乐家，连边表示音乐家的合作关系；

2) 线虫的神经网络（CE）[26]，节点表示线虫的神经元，边表示神经元突触；

3) 美国航空网络（USAir）[27]，网络中的每个节点对应一个机场，连边表示两个机场之间有直飞的航线；

4) 佛罗里达海湾雨季的食物链网络 (FWFB)[28]，网络中的每个节点表示一种生物，边表示生物之间捕食关系。

以上4个网络的基本结构参数如表1所示。

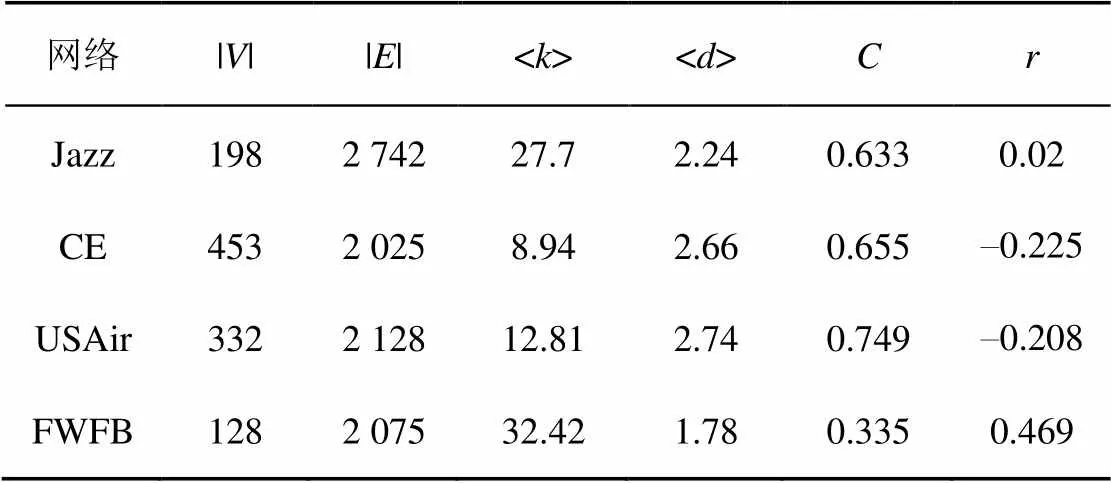
表1 静态网络数据集拓扑特征参数

其中，||表示网络中节点的个数，||表示边的数量，<>表示网络的平均度，<>表示网络平均距离，表示网络簇系数，表示结合系数。

5.2 度量指标

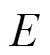
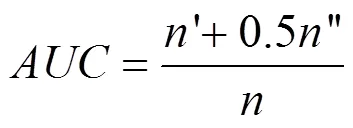
5.3 实验对比分析

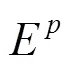
表2 Jazz网络中的AUC计算结果

表3 CE网络中的AUC计算结果

在爵士音乐家合作网数据集中的计算结果如表2所示。从计算结果可以看出，在该网络数据集中，基于复杂网络动力学模型的链路预测方法整体表现不如原始方法，只有基于复杂网络动力学模型的AA指标略高于原始AA指标。在基于复杂网络动力学模型的方法中，AA指标精确度最高。

在线虫的神经网络数据集中的计算结果如表3所示。基于复杂网络动力学模型的链路预测方法中，Salton指标、Sørenson指标、HPI指标、HDI指标、LHN-I指标相比原始方法的精确度有大幅度的提高，AA指标与RA指标计算结果非常接近，原始方法略好于基于复杂网络动力学模型的方法。同时，基于复杂网络动力学模型的精确度值与AA指标、RA指标较为接近，而原始方法的精确度与AA指标、RA指标相差较远。在基于复杂网络动力学模型的方法中，RA指标精确度最高。

表4 USAir网络中的AUC计算结果

表5 FWFB网络中的AUC计算结果

在美国航空网络数据集中的计算结果如表4所示。基于复杂网络动力学模型的链路预测方法中，Salton指标、Sørenson指标、HPI指标、HDI指标、LHN-I指标比原始方法的精确度有大幅度的提高，特别是LHN-I指标的精确度从0.764 5提高至0.943 7，AA指标与RA指标计算结果较为接近，原始方法好于基于复杂网络动力学模型的方法。在基于复杂网络动力学模型的方法中，RA指标精确度最高。

在佛罗里达海湾雨季的食物链网络数据集中的计算结果表5所示，基于复杂网络动力学模型的链路预测方法全部高于原始方法，同时基于复杂网络动力学模型的HDI指标计算数值最高，较其他计算指标有大幅度的提高。

6 结束语

链路预测是复杂网络研究的一个重要部分，具有广泛的理论研究和实际应用价值。本文在现有链路预测方法的基础上，通过引入复杂网络动力学模型，提出了基于复杂网络动力学模型的链路预测方法。通过实验部分可以看出，本文所提出的基于复杂网络动力学模型的链路预测方法具有有效性，在选择的真实网络数据集的实验中，大多数链路预测指标较原始方法有所提升，部分指标甚至有较大幅度的提升。本文的研究结果说明，传统的基于拓扑结构的研究方法结合复杂网络动力学模型，能够更全面地反映出网络节点与拓扑结构的本质规律和关系。然而，由复杂网络动力学模型的定义可以看出，基于复杂网络动力学的链路预测方法运算复杂度极高，在大规模网络中使用时的计算量非常巨大，不具有实用性。因此，在下一步的研究中，将着重关注其简化方法的研究。同时，本文只考虑了无权无向网络的链路预测，对于加权网络和有向网络并未涉及，在相关研究中关注到，复杂网络动力学模型能够很好地刻画加权网络和有向网络的结构特征和动态属性，考虑复杂网络动力学模型在加权网络和有向网络的链路预测中的研究也是下一步的重要方向。

[1] LYU L, ZHOU T. Link prediction in complex networks: a survey[J]. Physica A: Statistical Mechanics and its Applications, 2011, 390 (6): 1150-1170.

[2] CANNISTRACI C V, ALANISLOBATO G, RAVASI T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks[J]. Scientific Reports, 2015, 3 (4): 1613.

[3] KOSSINETS G. Effects of missing data in social network[J]. Social Networks, 2006, 28 (3): 247-268.

[4] 刘树新, 季新生, 刘彩霞, 等. 一种信息传播促进网络增长的网络演化模型[J]. 物理学报, 2014, 63 (15): 158902-158902.

LIU S X, JI X S, LIU C X, et al. A complex network evolution model for network growth promoted by information transmission [J]. Acta Phys. Sin, 2014, 63 (15): 158902.

[5] 刘树新, 季新生, 刘彩霞, 等. 局部拓扑信息耦合促进网络演化[J]. 电子与信息学报, 2016, 38 (9): 2180-2187.

LIU S X, JI X S, LIU C X, et al. Information coupling of local topology promoting the network evolution [J]. Journal of Electronics & Information Technology, 2016, 38 (9): 2180-2187.

[6] MITZENMACHER M. A brief history of generative models for power law and lognormal distributions[J]. Internet Mathematics, 2004, 1 (2): 226-251.

[7] KATZ L. A new status index derived from sociometric index[J]. Psychometrika, 1953, 18 (1): 39-43.

[8] CLAUSET A, MOORE C, NEWMAN M E. Hierarchical structure and the prediction of missing links in networks[J]. Nature, 2008, 453(7191): 98.

[9] LIU S, JI X, LIU C, et al. Extended resource allocation index for link prediction of complex network[J]. Physica A Statistical Mechanics & Its Applications, 2017, 479: 174-183.

[10] YU H T, WANG S H, MA Q Q. Link prediction algorithm based on the Choquet fuzzy integral[J]. Intelligent Data Analysis, 2016, 20(4): 809-824.

[11] SAMANTA S, Pal M. Link prediction in social networks[J]. Springer Briefs in Computer Science, 2018: 246-250.

[12] LU Y, GUO Y, KORHONEN A. Link prediction in drug-target interactions network using similarity indices[J]. Bmc Bioinformatics, 2017, 18(1): 39.

[13] LIU S, JI X, LIU C, et al. Similarity indices based on link weight assignment for link prediction of unweighted complex networks[J]. International Journal of Modern Physics B, 2017, 31 (2): 412-1054.

[14] 任晓龙, 吕琳媛. 网络重要节点排序方法综述[J]. 科学通报, 2014, 59(13): 1175-1197.

REN X L, LYU L Y. Review of ranking nodes in complex networks[J]. Chinese Science Bulletin, 2014, 59(13): 1175-1197.

[15] ADAMIC L A, ADAR E. Friends and neighbors on the Web[J]. Social Networks, 2003, 25 (3): 211-230.

[16] RAVASZ E, SOMERA A L, MONGRU D A, et al. Hierarchical organization of modularity in metabolic networks[J]. Science, 2002, 297(5586): 1551-1555.

[17] LIU Y Y, SLOTINE J J, BARABASI A L. Controllability of complex networks[J]. Nature, 2011, 473(7346): 167-173.

[18] JIA T, BARABÁSI A L. Control capacity and a random sampling method in exploring controllability of complex networks[J]. Scientific Reports, 2013, 3: 2354.

[19] 孔江涛, 黄健, 龚建兴, 等. 基于复杂网络动力学模型的无向加权网络节点重要性评估[J]. 物理学报, 2018, 67 (9): 255-271.

KONG J T, HUANG J, GONG J X, et al. Evaluation methods of node importance in undirected weighted networks based on complex network dynamics models[J]. Acta Phys Sin, 2018, 67(9): 255-271.

[20] SALTON G, MCGILL M J. Introduction to modern information retrieval[M]. Auckland: McGraw-Hill, 1983.

[21] ZHOU T, LYU L, ZHANG Y C. Predicting missing links via local information[J]. European Physical Journal B, 2009, 71(4): 623-630.

[22] LEICHT E A, HOLME P, NEWMAN M E. Vertex similarity in networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2006, 73(2): 026120.

[23] ADAMIC L A, ADAR E. Friends and neighbors on the Web[J]. Social Networks. 2003, 25(3): 211-230.

[24] PAN L, ZHOU T, LYU L, et al. Predicting missing links and identifying spurious links via likelihood analysis[J]. Scientific Reports, 2016, 6: 22955.

[25] GLEISER P M, DANON L. Community structure in Jazz[J]. Advances in complex systems, 2003, 6(4): 565-573.

[26] WATTS D J, STROGATZ S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 393(6684): 440-442.

[27] BATAGELJ V, MRVAR A. Pajek-program for large network analysis[J]. Connections, 1998, 21(2): 47-57.

[28] ULANOWICZ R E, HEYMANS J J, EGNOTOVICH M S. Network analysis of trophic dynamics in south florida ecosystems, FY 99: the graminoid ecosystem[R]. 2000.

Link prediction method based on complex network dynamics model

PAN Yonghao, YU Hongtao, WU Yiteng

National Digital Switching System Engineering and Technological R&D Center, Zhengzhou 450002, China

Link prediction is an important part of the study of missing links and future formations in complex networks. Currently, network structure-based link prediction methods are rich in results. Research on link prediction based on complex network dynamics model is rare. Firstly, a complex network dynamics model for unlicensed and undirected networks was constructed. Then the quantitative evaluation index of the link prediction node centrality based on the complex network dynamics model was given. Finally, the link prediction method defined by the complex network dynamics model was proposed by the given node centrality quantitative index. Experiments on real network datasets show that the proposed link prediction method has obvious prediction accuracy improvement.

complex network, link prediction, network dynamics

The National Natural Science Foundation of China(No.61803384)

TP393

A

10.11959/j.issn.2096−109x.2019065

潘永昊（1992− ），男，甘肃金昌人，国家数字交换系统工程技术研究中心硕士生，主要研究方向为复杂网络、链路预测。

于洪涛（1970− ），男，辽宁丹东人，博士，国家数字交换系统工程技术研究中心研究员，主要研究方向为网络大数据分析与处理。

吴翼腾（1992− ），男，山东乐陵人，国家数字交换系统工程技术研究中心博士生，主要研究方向为复杂网络链路预测、对抗样本等。

论文引用格式：潘永昊, 于洪涛, 吴翼腾. 基于复杂网络动力学模型的链路预测方法[J]. 网络与信息安全学报, 2019, 5(6): 67-74.

PAN Y H, YU H T, WU Y T. Link prediction method based on complex network dynamics model[J]. Chinese Journal of Network and Information Security, 2019, 5(6): 67-74.

2019−01−10；

2019−03−20

潘永昊，panyounghao2016@163.com

国家自然科学基金资助项目（No.61803384）