不同地质条件下地埋管热响应测试分析与比较

(上海工程技术大学 机械与汽车工程学院,上海 201620)

0 引 言

地源热泵节能、环保、无污染，节省建筑面积，经济效益高，使用寿命常长[1]。《地源热泵系统工程技术规范》[2]明确规定设计地埋管地源热泵系统方案前，应对工程场区内岩土体地质条件(包括岩土体热物性)进行勘察。在实际设计施工过程中,地质情况复杂多变，岩土热物性参数不准确，会导致设计负荷与实际负荷不符，影响地埋管换热器的准确设计[3]。设计人员在某岩土导热系数范围内会选择较低值，这往往造成系统规模过大。Cane和Forgas[4]曾经指出，地下换热器的设计尺寸一般都超出实际尺寸的10%～30%。S.P.Kavanaugh[5]研究表明，导热系数或导温系数10%的误差将导致4.5%～5.0%的地埋管设计长度误差。可见，准确测量岩土热物性参数对设计的合理性以及节省工程初投资都十分关键。

国内外学者对此做了大量相关研究。于明志[6]等人对测试时间、岩土初始温度和管间距进行分析研究，建议60 h的测试时长，初始地温测试深度10 m为宜，以及管间距越大，导热系数越小等结论。胡平放[7]等人通过建立三维数值模拟模型，分析了测试时间、计算开始与结束时间、比热容等因素对导热系数、热阻的影响。Georgios[8]作了热响应测试并分析了影响测试结构的两个主要因素：热流引起的土壤温度变化，施加热流的变化。目前，热响应试验是获取地下岩土热物性参数的主要措施。项目分别对长三角三地进行岩土热响应测试，经过实验，三处热响应测试在稳定状态下地埋管的进出口温度均能满足地源热泵机组地源侧供水温度的要求，为不同地质环境下地源热泵的设计施工提供一定参考依据。

1 传热模型

线热源模型由Mogensen首先提出[6]，Carslaw等人首次使用后，逐渐在多个国家推广开来[7]。线热源模型认为钻孔的直径相对于钻孔的深度来说非常小，可以将地埋管近似看做一个线性热源，将地埋管换热器周围的土壤看做无限大传热介质。当运行时间足够长时，可得到以下公式

(1)

式中Tf——供回水管理论平均温度/℃；

Tff——土壤初始温度/℃；

Q——输入的热量，即加热器加热功率/W；

H——钻孔深度/m；

λs——岩土导热系数/W·(m·℃)-1;

ρscs——岩土体积热容/J·(m3·℃)-1;

τ——测量时间/s；

γ——欧拉常数，取γ=0.577 216；

R0——钻孔内总的热阻/(m·℃)·W-1;

db——钻孔直径/m，取db=0.15 m。

式(1)可简化为

Tf=mlnτ+b

(2)

这里m和b是定值。

(3)

(4)

由式(2)可以得出m是导热系数的一个参数

(5)

钻孔内的传热热阻为

(6)

式中D——上升管与下降管轴心之间的距离；

d1——埋管内径;

d2——埋管外径；

h——流体与管壁之间的对流换热系数;

kp、kb、ks——管壁、回填材料和岩土的导热系数；

R0——钻孔内的传热热阻。

2 测试与分析计算

2.1 工程概况

工程所在地均处于夏热冬冷地区，莫干山地处北纬30°36’，东经119°52’，位于浙江湖州德清县，钻孔海拔高度342 m；浦江镇地处北纬31°12’，东经121°38’，隶属于上海市闵行区，平均海拔4.3 m；盐城市地处北纬32°34′～34°28′，东经119°27′～120°54′之间。前期进行地质测试分析，莫干山地处山区，除去表层较浅的房渣土，其他均为岩石结构，质地坚硬，结构组成较为单一；浦江属于长三角冲积平原，上层以淤泥为主；又因为沿海，故中下层以砂砾为主；盐城属于沿海城市，地质结构以粉砂层居多，且均具有较高的含水率。表1为各地埋管及回填材料相关参数。

2.2 实验仪器

热响应试验依托我方研制的岩土热物性参数测试仪进行，设备原理图如图1所示，该装置由贮热(加热)水箱、制冷系统(压缩机、浸没式蒸发器、风冷冷凝器)、水泵(变频控制)、流量调节阀、流量计、自控系统、温度传感器、温度采集仪及检测、记录仪表组成。测试仪中的管路与地热换热器地下回路相接，循环水泵驱动流体在回路中循环流动，流体经过加热器加热后流经地下回路与岩土进行换热。

整个测试过程依据《地源热泵系统工程技术规范》(GB50366-2009)“附录C 岩土热响应实验”进行，采用恒热流法进行排热工况测试，使用DataManagement读写软件进行数据的读写与处理，数据采集间隔为1 min，测试结束前后温度传感器和流量传感器均进行了标定与校正，保证了测试结果的稳定性。具体测试参数见表2。

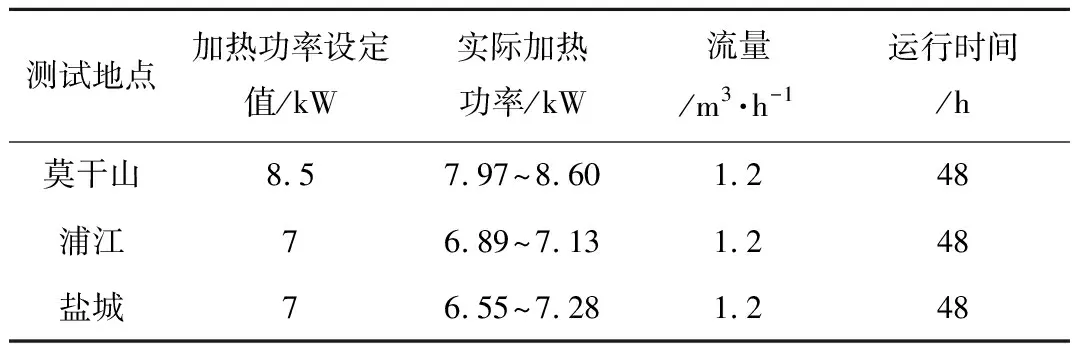
表2 热响应试验测试参数表

2.3 数据处理与分析

依据仪器上安装的数据采集软件实时采集的地埋管进出口水温、循环水流量等数据，可计算出不同时刻的进出口水温温差、进出口水温平均温度、排热量等数据。分别分析这些参数，得到如图2～图4所示的曲线。

结合图2～图4，对所测得的三地稳定工况运行数据进行汇总，如表3所示。

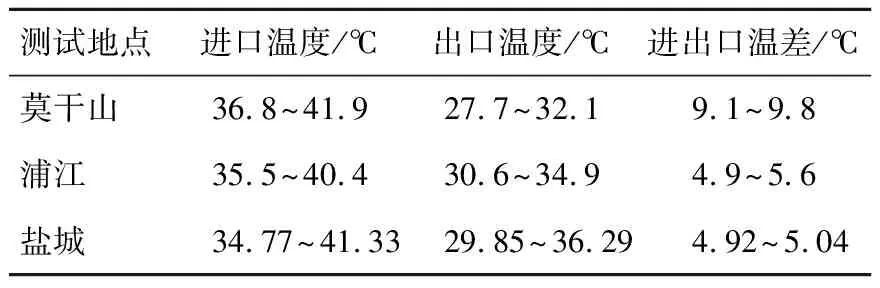
表3 工况稳定时测得的实验数据

由图2可知，莫干山岩土热响应测试孔在测试开始4 h内，地埋管温度上升较快，这是因为岩石具有较强的蓄热能力及热惰性，在测试初始阶段，测试孔内换热量不大，地埋管进口温度急剧上升；又由于岩石热扩散性较好，4 h之后，地埋管内热量逐渐释放至周围区域，换热量逐渐增大，4～8 h内属于热扩散整流阶段，8 h后供回水温差趋于稳定，说明换热趋于稳定，同样由于岩石的高热扩散性，在换热趋于稳定后，地埋管进口温度上升幅度大幅下降，趋于平缓。稳定后的供水温度是36.8～41.9℃，供回水温差9.1～9.8℃。

由图3可知，浦江岩土热响应测试在测试初期，即开始4 h内，地埋管进出口水温上升较快，因为在测试初期，地埋管内存水与岩土体初始温度相同，贮热水箱内水温也接近大气温度，埋管进出口水温温差很小，随着贮热水箱内水温因电加热器工作而持续升高，即地埋管进出口水温温升很快，出口水温也随之上升，进出口水温温差逐渐增大，随着循环水与岩土体之间的换热不断进行，进出口水温温差也趋于稳定，基本处于4.9～5.6℃之间。

由图4可知，盐城岩土热响应测试自开始实验5 h换热基本稳定，而后地埋管换热器进口水温为34.77～41.33℃，出口水温为29.85～36.29℃，温差为4.92～5.04℃，排热量为7.15～7.33℃。盐城相较其他两地，没有较大的温升区间，亦没有较大的波动，整体工况相对平稳，这与其地处沿海区域，受自身的粉砂层地质以及较高的含水率影响较大。

结合式(2)，用曲线拟合法，得出Tf对应lnτ的直线，其斜率即为m。已知m值结合式(5)，可算出导热系数λ。

图5是三地地埋管进出口平均温度随时间对数的变化趋势，针对不同地区分别选取适当的数据区间进行线性拟合，即图6～图8。将分析结果进行汇总如表4所示。

表4 线性拟合结果

由表4可知，莫干山拟合公式中，斜率m=3.169 2，截距b=0.696，结合公式(5)，可以计算出莫干山的岩土导热系数为λ1=2.40 W/(m·℃)，同理，结合表4中浦江和盐城的拟合公式，可以得出其岩土导热系数分别为：浦江λ2=1.92 W/(m·℃)，盐城λ3=1.84 W/(m·℃)。根据所选定的地埋管结构，由公式(6)计算出钻孔的热阻Rb，将升温曲线的截距b代入公式(4)，可以计算得出岩土热扩散率。最终获得的岩土热物性参数如表5所示。

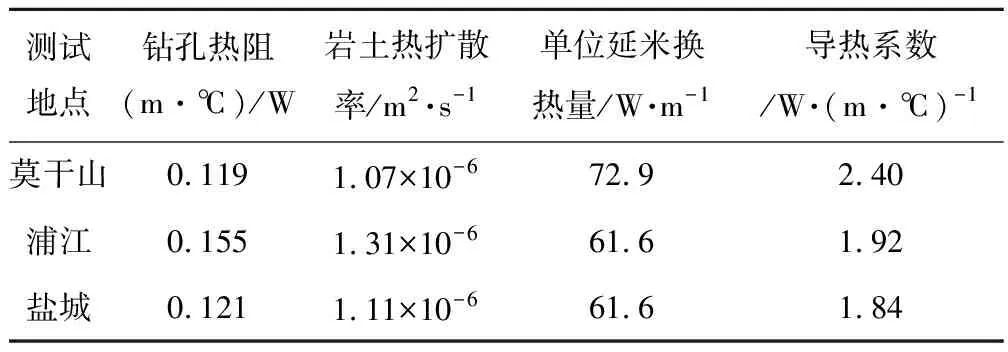
表5 岩土热物性参数

对比表5中三组数据可以发现：三地钻孔热阻和岩土热扩散率比较接近，其中莫干山岩土导热系数2.40 W/(m·℃)，钻孔热阻0.119(m·℃)/W；浦江岩土导热系数1.92 W/(m·℃),钻孔热阻0.155(m·℃)/W；盐城岩土导热系数1.84 W/(m·℃)，钻孔热阻0.121(m·℃)/W。综合来看，莫干山钻孔热阻最小，岩土导热系数最高，换热效果相对较好。

3 结果分析

(1)岩石具有高蓄热能力和热惰性，使地埋管换热器前期与周围岩土换热较慢，同时岩石具有的高热扩散性，使其在之后的热扩散整流阶段能与周围土壤高效快速换热，这对地埋管换热器的换热起到积极作用。与其他地质条件相比，岩石地质钻孔较为困难，但其较高的换热效果说明在岩石地质条件下地源热泵亦有存在的必要。

(2)与其他两地相比，浦江白天排热工况波动较大，晚上趋于平缓。分析原因，可能是白天电网电压不稳定，电加热器正常运行受到一定影响。在整个测试阶段，要保证恒定的热量输入，所以测试期间需使用稳压电源等一些辅助设备。

(3)由表1和图2～图4可以看出，前期换热效果可能会受岩土初始温度影响，但后期稳定阶段，主要影响地埋管换热器换热能力的是岩土导热系数和钻孔热阻。岩土导热系数越大，钻孔热阻越小，后期进出口平均温度的值就越高。

(4)测试过程中，在不同的加热功率下，排热工况下单位延米的换热量是不相同的，所以设计单位不能简单地把“单位延米换热量”作为设计依据应用于地下换热系统设计中。地下换热器设计计算应按照国家标准《地源热泵系统工程技术规范》(GB50366-2009)，首先进行全年逐时动态负荷计算，最小计算周期宜为1年，继而计算全年地下换热系统总排热量与其总吸热量，根据计算结果做好热平衡措施，同时还需结合岩土体热物性参数，采用专用软件进行地下换热器设计。

4 结 论

(1)对测试数据进行计算分析，得到莫干山岩土导热系数2.40 W/(m·℃)，单位延米换热量72.9 W/m；浦江岩土导热系数1.92 W/(m·℃)，单位延米换热量61.6 W/m；盐城岩土导热系数1.84 W/(m·℃)，单位延米换热量61.6 W/m。

(2)在野外进行热响应实验时，要使用稳压装置以保证恒定的热量输入。

(3)岩石地质条件一般具有较高的热扩散性，对地埋干换热器换热效果有促进作用。

(4)地埋管换热器换热效果前期受岩土初始温度影响较大，运行稳定阶段受导热系数和热阻影响较大。

(5)不能用单位延米换热量这个单一参数分析地埋管换热器换热效果。