粒子群优化算法中惯性权重改进策略综述
杨博雯,钱伟懿
(渤海大学 数理学院, 辽宁 锦州 121013)
0 引言
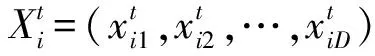
(1)
(2)
其中c1和c2是学习因子,r1和r2是[0,1]之间的随机数.为了改善基本PSO算法的性能,Shi 和Eberhart〔2〕引入了惯性权重策略,其速度更新公式为
(3)
其中ω称为惯性权重.引入惯性权重能够较好地平衡了PSO算法的全局搜索能力和局部搜索能力.后人把带有惯性权重的PSO算法称为标准PSO算法.自从引入惯性权重后,人们对PSO算法中的惯性权重进行了广泛深入的研究,取得许多好的成果.为了让读者较快了解这些成果,为PSO算法进一步研究提供一些参考,本文从五个方面对PSO算法中的惯性权重改进策略进行综述研究.
本文常用的符号说明:rand()为[0,1]之间的随机数,ωmin和ωmax分别为惯性权重的最小值(或终值)和最大值(或初值),t为当前迭代步,T为最大迭代步,N为群体规模,D为搜索空间的维数.
1 常值惯性权重策略
所谓的常值惯性权重就是标准PSO算法在实施过程中惯性权重值为常数.事实上,基本PSO算法就是惯性权重等于1的标准PSO算法.由于惯性权重大,全局搜索能力较强,局部搜索能力较差,惯性权重小,全局搜索能力较差,局部搜索能力较强,为了平衡PSO算法的全局搜索能力和局部搜索能力,Shi 和Eberhart在文〔2〕中讨论了常值惯性权重的选择区域,当ω>1.2时,PSO算法具有较弱的全局搜索能力,当ω<0.8时,PSO算法易陷于局部最优,因此他们建议ω取[0.8,1.2]之间的值.Clerc在文〔3〕中建议取ω=0.729,c1=c2=1.494.Trelea在文〔4〕中通过对PSO算法的动态系统分析,建议取ω=0.6,c1=c2=1.7.张炎等在文〔5〕中通过大量实验,提出的策略.高浩等〔6〕在PSO算法中引入高斯变异算子,提出一种改进的PSO算法,在该文中建议取ω=0.7,c1=c2=1.4.虽然上述从不同的角度分析给出惯性权重取值方法,但常值惯性权重不适合各类问题,因此在实际应用中根据不同的问题选取适当的权重.
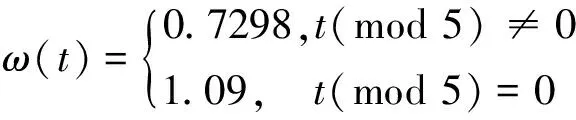
2 随机惯性权重策略
所谓随机惯性权重就是ω取随机值,它能够很好使PSO算法在动态环境下跟踪最佳状态.Eberhart和Shi〔7〕首先引入随机惯性权重策略,其表达式为
(4)
由(4)知,ω是[0.5,1]之间的随机数,均值为0.75.
黄轩等〔8〕通过取ω从0.1到1间隔0.1的值的实验发现:对于单峰函数,ω取值在[0.3, 0.5]内较好,对于多峰函数ω取值在[0.5, 0.7]内较好,基于实验分析,他们提出一个随机惯性权重策略
ω=0.4+0.2·rand()
即ω取[0.4, 0.6]内的随机数.
赵志刚等〔9〕对简化PSO算法提出一种新的随机惯性权重策略,其公式如下:
ω=ωmin+(ωmax-ωmin)·rand()+σ·randn()
(5)
其中randn()为服从正态分布的随机数,σ为用来衡量权重与其均值之间的偏离程度,(5)中第3项控制权重向期望权重方向进化.
Lei等〔10〕基于模拟退火策略随机调整惯性权重,其方法如下:设k是一正整数,当前迭代步t是k的倍数时,首先计算模拟退火温度

惯性权重定义为
其中α1,α2是[0,1]之间的随机数,且α1>α2.当t不是k的倍数时,惯性权重采用线性递减策略,见式(8).
张丽平等〔11〕基于最佳适应值的变化率给出了一种随机调整惯性权重策略,即

Adewumi等〔12〕提出基于成功率的自适应随机惯性权重策略,对于极小优化问题,首先定义了当前迭代步群体成功率
(6)
其中
(7)
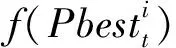
ω(t)=0.5×rand()+0.5×ssrt-1
胡建秀等〔13〕将惯性权重与学习因子联系在一起,给出了惯性权重的随机策略,即
ω(t)=1-c1r1-c2r2
其中r1和r2是[0,1]之间的随机数,c1和c2是学习因子.
3 时变惯性权重策略
所谓时变惯性权重就是基于算法的迭代步来确定惯性权重.目前关于时变惯性权重主要有两方面:一是惯性权重线性递减(或递增)策略,另一种是惯性权重非线性递减(或递增)策略.
3.1 线性策略
为了平衡PSO算法的全局搜索能力和局部搜索能力,一般情况下,在算法的初期惯性权重较大,增强算法全局搜索能力,而在算法的后期惯性权重较小,提高算法的局部搜索能力,基于此思想,Shi和Eberhart在文〔2〕中提出了惯性权重线性递减策略,惯性权重更新公式为
(8)
一般情况下,取ωmin=0.4,ωmax=0.9〔14,15,16〕,但有些情况下,ωmin,ωmax取0.4和0.9以外的值〔17,18〕.
通过具体分析,Zhang等〔19〕提出了惯性权重递增策略,即
在该文中,取ωmin=0.4,ωmax=0.9,虽然数值实验验证了在某些问题上优于线性递减策略,但是进一步研究工作较少.
若取ωmin=0.4,ωmax=0.9,则线性递减策略使惯性权重从0.9线性减小到0.4,而线性递增策略使惯性权重从0.4线性增加到0.9.崔宏梅等〔20〕在前面两个工作基础上,提出了惯性权重先增后减策略,惯性权重从0.4线性增加到0.9,然后在线性递减到0.4,即
3.2 非线性策略
惯性权重线性递减策略比较简单,且易实现,但惯性权重沿着线性方向递减是否最好呢?一些学者根据惯性权重递减思想,提出惯性权重非线性递减策略.Chatterjee和 Siarry〔21〕提出了一类抛物线形式递减的惯性权重调整策略,即
(9)
其中n是非线性调整常数,不同的n导致不同的惯性权重非线性递减策略,显然n=1就是线性递减策略.同时,陈贵敏等〔22〕提出两种抛物线形式的惯性权重递减策略,一种是凹型抛物线(开口向下)形式,即
(10)
另一种是凸型抛物线(开口向上)形式,即
(11)
(10)式惯性权重初期递减较慢,后期递减较快,(11)式惯性权重初期递减较快,后期递减较慢.事实上,(11)式惯性权重公式就是(9)式n=2的情况,同样的结果在文〔23〕也给出过.Huang等〔24〕把文〔21〕的结果进行推广,给出一种更广泛的惯性权重调整策略
(12)
显然若参数m取1,就是(9)式形式.在该文中,作者对m=2,n=1,m=1,n=2,m=2,n=5三种策略进行实验,实验结果表明取m=2,n=5效果较好.Liu等〔25〕根据不同的适应值,提出两种动态非线性方法调节惯性权重策略,一种惯性权重调整表达式如下:
(13)
另一种表达形式
(14)
其中dn是动态非线性因子,dnmax和dnmin是dn的最大值和最小值.该文中,两种策略使用方法为当适应值小于平均适应值时,采用(13)式或(14)式.
与上述探讨角度不同,一些学者提出按指数方式调整惯性权重策略.Jiang等〔26〕提出惯性权重按指数方式调整策略,即
(15)
其中ρ为控制参数.Lei等〔27〕在此基础上,提出另一种按指数方式调整惯性权重策略
(16)
其中b为参数,显然,当b=1,ρ=30时,两种策略是一样的.Ting等〔28〕基于文〔29〕的差分进化算法的自适应交叉率的调整方案,给出的惯性权重调整策略
(17)
其中a,b为非负参数.事实上,该结果是对文〔26,27〕的结果进行了推广,即,当b=1时就是(15)式,当a=30时就是(16)式.(17)式中a越大,局部搜索能力越大,b越大,全局搜索能力越大.Chen等〔14〕基于惯性权重线性递减的框架,提出两种惯性权重按指数方式递减策略,具体表达式见(18)和(19).
(18)
(19)
惯性权重采用(18)式的PSO算法称为e1-PSO, 采用(19)式的PSO算法称为e2-PSO,在取ωmin=0.4,ωmax=0.9条件下,数值结果验证了e2-PSO优于e1-PSO,而他们都优于线性递减策略.张迅等〔30〕推广了(19)式的结果,他们给出的惯性权重调整策略为
其中k为参数,显然,当k=0.25时,与(19)式策略相同.通过分析,当k>0.3时,惯性权重变化平稳,当k<0.3时,在算法的初期惯性权重较大,且递减速度较快,而在算法后期,惯性权重相对平稳,因此作者建议k取值在[0.1,0.3]之间,为了减少计算权重次数,提高算法的效率,作者提出如下惯性权重调整策略
数值结果认为k=0.2效果较好.为了克服PSO算法早熟现象和后期震荡现象,Li等〔31〕给出另一种按指数方式递减惯性权重策略,即
其中d1,d2是参数,大量实验表明,当ωmin=0.4,ωmax=0.95,d1=0.2,d2=7时,算法性能可以大大提高.Amoshahy 等〔32〕提出一种灵活(Flexible)的指数惯性权重策略,即
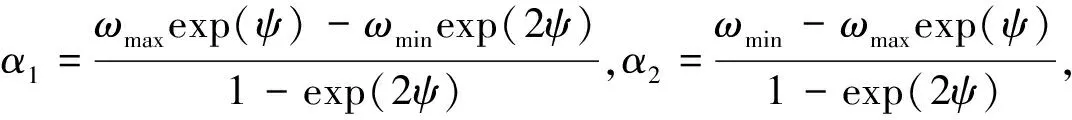
其中c是调节参数,c值较大,则惯性权重下降快,使算法过早陷入局部搜索,c值较小,则惯性权重下降慢,使算法在后期也不能接近ωmin,因此,作者建议取c=10.再如,文〔33〕给出的惯性权重策略
ω(t)=ω×u-t
其中ω是取[0,1]之间的初始惯性权重值,u是取值于[1.0001,1.005]之间的常数.实验表明,u=1.0002,ω∈[0.3,0.4]算法能够得到较好的结果.
除此之外,许多学者从不同的角度提出一些其他惯性权重非线性调整策略.Malik等〔34〕提出Sigmoid递减和递增的惯性权重策略,即
(20)
(21)
其中u=10(log(T)-2),n是设置sigmoid函数分区的常量,(20)式称Sigmoid递减的惯性权重,(21)称Sigmoid递增的惯性权重.数值实验显示Sigmoid递增的惯性权重大大提高了快速收敛能力.田东平等〔35〕提出了另一种基于Sigmoid函数的非线性递减惯性权重策略,即
不难计算该策略的初始权重为0.95,最终权重为0.4,实验结果表明了该策略优于惯性权重线性递减方法和文〔22〕的三种方法.黄洋等〔36〕也提出了基于Sigmoid函数的非线性递减惯性权重另一种策略
以上三种基于Sigmoid函数调整惯性权重策略,都是利用Sigmoid函数特征,使得在算法的初期和后期惯性权重递减缓慢,这样在算法初期能够保证惯性权重长时间取得较大值,增强全局搜索能力,在算法后期也能保证惯性权重长时取得较小值,增加局部搜索能力.
Gao等〔37〕提出了对数递减的惯性权重策略
该策略能够改善收敛速度.Lei等〔38〕使用Sugeno函数作为惯性权重下降曲线,给出惯性权重非线性递减策略
其中s是大于-1的常数.该策略能够自动调整全局搜索能力和局部搜索能力.
Kentzoglanakis等〔39〕提出三个惯性权重振荡调整策略,策略一:振幅为常数按余弦波方式振荡调整惯性权重,当t≤T1时,
(22)
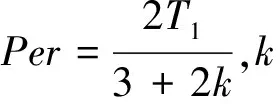
(23)
策略三:分段调整惯性权重,即
(24)
Kordestani等〔40〕把线性递减惯性权重与线性递增惯性权重思想相结合提出按对称三角波方式调整惯性权重策略,称为振荡三角惯性权重,其表达式如下:
ω(t)=ωmax-|round(αx)-αx|
其中参数α∈[0.0,0.5],不同的α生成不同三角波形式来调整振荡三角惯性权重,而round(x)是实数x的四舍五入函数.由于惯性权重振荡变化,所以这两种策略有效平衡了全局搜索能力和局部搜索能力.
姜建国等〔41〕基于余弦函数提出了非线性递减的惯性权重调整策略
该策略在一定程度上改进了算法的搜索效率,且克服算法早熟现象.黄洋等〔42〕在文〔9〕和〔41〕基础,提出一种动态调整惯性权重策略,即
其中σ为调整因子,betarnd()为服从Beta 分布的随机数.该策略中前两项为惯性权重按余弦方式递减,第三项控制惯性权重偏离程度,在一定程度上,克服了在算法后期群体多样性较差现象.姜长元等〔43〕提出了惯性权重按正弦方式调整策略,即
显然,该策略惯性权重从0.4按正弦曲线形式递增到0.9,然后再按正弦曲线形式递减到0.4.南杰琼等〔44〕基于正弦函数把惯性权重非线性递减策略与随机策略相结合提出了改进的惯性权重调整策略
该策略第一项惯性权重按凸曲线形式从ωmax递减到0,而第二项是随机扰动项,在算法前期扰动范围较小,后期扰动较大,从而有效平衡了全局搜索能力和局部搜索能力.李建平等〔45〕提出一种基于逆不完全Γ函数惯性权重非线性递减策略,即
(25)
其中λ是非负参数,该文取λ=0.1,gammaincinv(λ,a)是逆不完全Γ函数.(25)式从略大于ωmax递减到接近于ωmin,且前期接近线性递减,后期接近指数递减,所以该策略能够较好实现全局搜索能力和局部搜索能力的平衡.Li等〔46〕基于正切函数提出一种非线性递减惯性权重调整策略
其中k是一个控制参数,它的不同导致惯性权重递减方式不同,该文通过数值实验认为k=0.6或k=1.7能够得到较好数值结果,该文中取k=0.6.
4 混沌惯性权重策略
由于混沌映射具有遍历性和随机性等优点,所以被广泛地应用于优化领域.混沌惯性权重的基本思想就是利用混沌映射的优点来设定惯性权重.Feng等〔15〕利用Logistic映射
z=μ×z×(1-z)
(26)
分别提出混沌递减惯性权重策略
和混沌随机惯性权重策略
ω(t)=0.5×rand()+0.5×z
其中μ=4.如果z的初始值取在(0,1)之间,且不等于0,0.25,0.5及1,那么(26)式能够生成(0,1)之间的数.该策略就是为了避免算法陷入局部最优,把Logistic映射与线性递减策略(8)和随机策略(4)相结合,从而改善了线性递减策略和随机策略的性能.数值结果表明该策略具有较好的收敛精度、较快的收敛速度和较好的全局搜索能力.
Arasomwan等〔47〕在文〔15〕的基础上,把群体成功率(6)与混沌映射相结合,提出了两个新的自适应惯性调整策略,即
(27)
ω(t)=0.5×ssrt+0.5×z
(28)
其中z=4×ssrt×(1-ssrt).显然该策略就是在文〔15〕的基础上,把(26)式右端中的z用群体成功率代替,另外,在(28)式中群体成功率代替了随机数.
Cheng等〔48〕基于正弦函数提出了一个新的混沌映射,即
(29)
其中z(t)为第t个混沌数,d是最大迭代数的分区数,取d=2或d=4.根据新的混沌映射提出了惯性权重调整策略,即
(30)
数值实验证明在某些问题上,该策略的寻优能力优于其他算法.Cheng等〔49〕基于Logistic映射给出了惯性权重更新策略
ω(t)=4×ω(t-1)×(1-ω(t-1))
文〔25〕中提出两个策略(13)或(14)只是适应值小于平均适应值所采用的惯性权重调整策略,而对于适应值大于平均适应值,则采用下面的混沌惯性权重调整策略
ω(t)=α+(1-α)×z
其中α是动态混沌惯性权重调整因子,αmax和αmin分别是α的最大值和最小值,z由(26)式给出.此外,其他混沌映射也能生成相应的惯性权重更新公式,具体见文〔50〕.
5 自适应惯性权重策略
时变惯性权重策略是惯性权重的变化只与迭代步有关,而没有考虑到算法的性能与惯性权重之间的关系,因此,惯性权重调整没有充分利用算法所提供的有用信息.基于这个思想,许多学者提出一些自适应惯性权重.所谓自适应惯性权重就是基于一个或多个反馈参数来调整惯性权重.Shi和Eberhart〔51〕提出模糊自适应PSO算法,在此算法中,建立一个9个规则的模糊系统来动态调整惯性权重,每一个规则有2个输入变量和一个输出变量,当前群体规范化的最优性能指标(Normalized current best performance evaluation, NCBPE)和当前的惯性权重作为输入变量,而惯性权重的改变量作为输出变量,NCBPE被计算如下:
其中CBPE为最优性能指标,CBPEmin为最小估计值,CBPEmax为非最优值.所有的三个模糊变量都有三个模糊集:低、中和高.以一个例子为例:如果NCBPE是中的,权重是低的,那么权重的改变量是高的.
Yang等〔52〕基于进化速度和聚集度两个参数提出一种自适应惯性权重策略,进化速度定义如下:


其中ωini是权重的初始值,本文取ωini=1,α和β是[0,1]之间的常数.该文对不同的α和β进行数值实验,结果表明该方法在计算复杂性,成功率和求解精度方面有一定的优势.
Arumugam 和Rao〔53〕利用群体历史最好适应值与每个粒子历史最好适应值的平均值的比,定义了自适应惯性权重
其中gbest是群体历史最好位置,besti是第i个粒子历史最好位置,f是适应值函数,
Panigrahi等〔54〕基于粒子的适应值最优排序给出了自适应惯性调整策略
其中Ranki是第i个粒子按最好适应值排序的位置,Total_population是群体规模,该策略是每个粒子拥有各自的惯性权重,显然较好的粒子有较小的惯性权重,具有局部搜索能力,较差的粒子有较大的惯性权重,具有全局搜索能力.
Shen等〔55〕基于群体多样性和群体的聚集度提出了自适应惯性权重调整策略
ωi(t)=ωmin+(ωmax-ωmin)×Ft×φt
其中Ft为多样性函数,φt为调整函数,其表达式如下
φt=exp(-t2/2σ2)
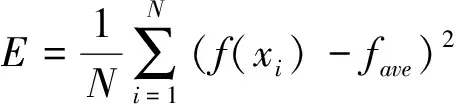
Zheng等〔56〕首先定义第i个粒子在第j维上的个体搜索能力为
(31)
其中xij是第i个粒子位置在第j维上的分量,pij是第i个粒子历史最好位置的第j维分量,pgj是全局最好位置的第j维分量,ε是一个很小的正常数.从(31)式可以看出,如果xij离pij较远,而pij离pgj较近,则ISA较大,此时说明全局搜索能力较强,应该减小惯性权重,增强局部搜索能力;如果xij离pij较近,而pij离pgj较远,则ISA较小,此时说明局部搜索能力较强,应该增大惯性权重,提高全局搜索能力.基于此思想,作者提出了自适应调整惯性权重策略
其中α∈(0,1]为控制惯性权重变化速度参数.实验表明α∈[0.1,0.4]时算法性能较好,该文取α=0.3.
Alfi〔57〕把自适应变异机制和动态调整惯性权重策略与传统PSO算法结合,提出自适应粒子群优化算法,惯性权重调整策略为
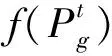
Zhan等〔58〕首先给出粒子i与其他粒子的平均距离
基于此距离定义了进化因子
其中dg为全局最好粒子与其他粒子的平均距离,dmin,dmax分别为所有di中最小值和最大值.基于进化因子和sigmoid函数提出了自适应调整惯性权重策略,即
该惯性权重策略主要依赖于进化因子,在算法早期,进化因子较大,惯性权重较大,有利于全局搜索,而在算法后期处于收敛状态,此时进化因子较小,惯性权重较小,有利于局部搜索.
Nickabdi等〔59〕首先定义了(6)式给出的群体成功率ssrt,如果ssrt值较大,粒子收敛到远离最优解的点,使得整个群体较慢向最优解移动,从而应增大惯性权重,相反,如果ssrt值较小,表明粒子在最优解附近振荡,从而应减小惯性权重.基于此思想,他们提出了如下惯性权重调整策略
ω(t)=g(ssrt)
其中g是递增函数.在该文中作者采用了线性函数,即
ω(t)=(ωmax-ωmin)ssrt+ωmin
显然ssrt∈[0,1],ω(t)∈[ωmin,ωmax]
Adewumi等〔12〕也基于群体成功率提出自适应惯性权重策略,即
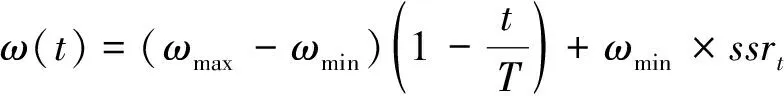
该策略使得最终惯性权重具有一定灵活性,最终惯性权重在ωmin附近获得可能更高或更低的值,即成功率较大,则最终惯性权重更高,成功率较小,则最终惯性权重更低,从而增加全局或局部搜索能力.
Kessentini等〔60〕基于最优粒子的反馈信息提出了一种自适应惯性权重策略.首先定义一个K维的变量d=(d(1),d(2),…,d(K)),其中K为常数.d的每个分量定义为
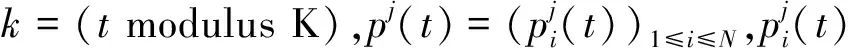
该策略当粒子的最优位置比较接近时,惯性权重将会增加,从而提高探索能力,每K步,惯性权重都有较小值,从而提高开发能力.
杜江等〔61〕提出一种新的自适应调整惯性权重策略
其中α为惯性权重调整参数,它由粒子在搜索空间的分布来决定,该文采用分布熵
来刻画搜索空间的分布,其中Q为搜索空间被平均划分的区域个数,Nk为t时刻第k个区域中粒子的个数,(k=1,2,…,Q).显然,E(t)越小表明粒子越集中,此时α应有较大的值,增加算法的搜索能力,反之,E(t)越大表明粒子越分散,此时α应有较小的值,增加算法的开发能力.基于此思想,作者提出调整参数α的策略,即
其中E1和E2分别为粒子分布熵的上、下门的阈值,且E1 周燕等〔62〕首先定义粒子适应值的相对变化率 其中fi(t)表示粒子i在t时刻的适应值.当粒子相对变化率k较大时,表明粒子远离最优解,此时应增大惯性权重,使粒子向最优解靠近,相反,当粒子相对变化率k较小时,表明粒子更新较差,此时应减少惯性权重,基于此思想,作者基于粒子相对变化率和Sigmoid函数提出了一个新惯性权重调整策略 顾明亮等〔63〕基于粒子适应值方差提出一个自适应调整惯性权重策略.粒子适应值方差定义为 其中fi为粒子i的适应值,fave为群体的平均适应值,f为归一化因子,它被定义如下 若粒子适应值方差小,则群体多样性差,此时应增大惯性权重值,因此惯性权重调整策略为 其中ε为适应值方差的临界值. 敖永才等〔64〕将粒子群体按粒子适应值变化情况分成两个子群体,即 对于极小问题,属于集合P1的粒子适应值得到改进,而属于集合P2的粒子适应值没有得到改进,此时惯性权重应赋予较小的值,因此对每个粒子定义了不同的权重,具体表达式如下: 其中ω(t)为(8)式的线性递减惯性权重. 李龙澍等〔65〕基于粒子对全局最优位置的距离提出动态调整惯性权重的策略.先引入粒子i在t时刻与全局最优位置的距离 惯性权重基于上式距离进行动态调整,其表达式如下: PSO算法是目前应用较广泛的一种智能优化算法,其惯性权重参数是PSO算法最重要参数,它直接影响算法的收敛速度和求解精度.本文对PSO算法的惯性权重改进策略从5个方面进行了较全面的综述,为研究人员对PSO算法的惯性权重研究提供一定的参考.由于作者水平有限,有许多惯性权重的改进策略没有被总结.未来的工作就是研究这些算法的性能,并合理利用已知的惯性权重策略,提高算法的性能.
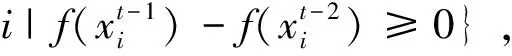

5 结论

