基于紧凑拉伸试验的含缺陷燃气管疲劳寿命预测分析*
吕彦伟,刘钦节,2,付 强,袁宏永,付 明
(1.安徽理工大学 能源与安全学院,安徽 淮南 232001;2.深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001;3.清华大学 合肥公共安全研究院,安徽 合肥 320601)
0 引言
随着天然气的使用规模越来越大,国内各地有关燃气管道的破坏事故时有发生。引发此类事故的原因众多,其中含初始缺陷管道的疲劳破坏是其主要原因之一[1]。管道在实际工作期间的输气量不稳定,且存在一定范围内的压力波动,对于含初始缺陷的燃气管道,此缺陷周围易产生较大的应力集中,管道更易在缺陷处出现裂纹扩展。当裂纹扩展至临界失稳尺寸时,管道产生疲劳断裂,最终导致泄漏。因此,分析燃气管泄漏发生的原因,预测燃气管疲劳寿命,对管道的日常维护管理以及制定相应措施具有重要意义。
鉴于此,钟勇等[2]利用理论推导寿命与实测结果对比的方法,验证不同应力强度因子下裂纹扩展速率与疲劳寿命的关系;蒋云等[3]对含缺陷管道疲劳寿命进行理论推导,得到预测管道寿命的方法;吴冰等[4]通过TC17合金材料进行疲劳裂纹扩展速率试验,结合裂纹容限相关理论,估算疲劳剩余寿命;邱保文等[5]采用基于失效评定图技术对油气管道的疲劳寿命进行计算和分析,并通过对比全尺寸实验结果验证计算的可靠性;马秋荣等[6]基于小试样疲劳实验分析,得出X60和X80管道在不同应力比下的疲劳裂纹扩展规律,并对X80含裂纹管道的疲劳寿命进行预测;余建星等[7]采用理论计算和数值模拟方法分析裂纹各种参数对海底管道疲劳寿命的影响作用。
综上所述,国内外学者对预测含缺陷管道寿命开展了大量研究,但鲜有利用裂纹扩展速率实验结合理论推导对工程实践条件下含缺陷燃气管道寿命进行预测和研究。本文拟利用断裂力学中的损伤容限分析方法推导含缺陷燃气管疲劳寿命预测模型,利用MTS电液伺服疲劳试验机开展疲劳裂纹扩展速率试验研究,分析含初始裂纹管道在交变压力作用下的裂纹扩展规律,为预测分析燃气管疲劳寿命、监测管道破坏过程及制定相应措施提供参考。
1 含缺陷管道疲劳寿命预测的理论模型
对于含有裂纹的燃气管道,在交变压力作用下,其寿命由裂纹扩展行为所决定。若外加应力水平较低、裂纹尺寸较小,相应的应力强度因子低于应力强度因子门槛值ΔKth时,裂纹不会扩展;反之亦然。因此,裂纹的扩展速率决定管道的使用寿命,而应力强度因子是评判含裂纹构件是否断裂及裂纹扩展速率的重要参量[8]。对于恒定幅值载荷,可以采用断裂力学中损伤容限分析法,通过积分裂纹扩展速率表达式预测管道的使用寿命。
国内外学者常用Paris公式研究裂纹扩展速率与寿命N的关系,其表达式为[9]:
da/dN=C(ΔK)m
(1)
式中:N为裂纹扩展到临界尺寸时的循环次数,cycle;da/dN为裂纹扩展速率,即每个循环下裂纹扩展量,mm·C-1;C,m为Paris的2个重要参数;ΔK为裂纹尖端应力强度因子。
管道泄漏多数是由于疲劳断裂造成的,其中最常见最危险的初始裂纹即为张开型裂纹(Ⅰ型裂纹),其主要表现为在压力的波动下,裂纹沿深度方向非稳定性扩展。为模拟实际管道中的泄漏情况,以表面缺陷裂纹最终扩展为穿透裂纹作为寿命结束的依据,即以管厚作为管道失稳的临界尺寸。现对管道上表面裂纹尖端的应力强度因子进行分析。
在1个壁厚为ac的管道表面上存在1个沿管道轴向方向的未穿透的半椭圆形表面裂纹,裂纹长轴和短轴分别为2a和2b。管道内压为p,该处的应力强度因子计算式为[2]:
(2)

仅考虑在裂纹最深处(θ=π/2)的应力强度因子为:
(3)
式中:KI深为在管壁上I型裂纹最深处的应力强度因子。
在一定交变工作压力下,裂纹最深处的应力强度因子:
(4)
将式(4)代入式(1)式,得:
(5)
在管道实际运行中,由于受到内压的循环加载作用,裂纹会沿径向扩展直至贯通,形成泄漏,造成破坏。所以,将式(5)用于表面裂纹沿深度方向的扩展时,应对其进行修正。蔡强康等[11]通过研究表明,裂纹沿轴向扩展量大致是沿径向扩展量的1.384倍。
令U=1.384,修正后表面半椭圆裂纹的径向扩展速率为:
(6)
对式(6)进行积分得:
(7)
综合疲劳裂纹扩展速率公式da/dN-ΔK及半椭圆表面裂纹的尖端应力强度因子的方程,可得循环周次计算公式为:
(8)
通过分析可以得出,参数C和m、燃气管中的内压变化值Δp、疲劳裂纹容限尺寸ac以及初始裂纹尺寸a0对工程实践中燃气管疲劳寿命N有重要影响作用。
2试验材料与方法
2.1 试验设计
试样取自于安徽淮南天然气二气源管道工程,管径为DN400,设计能力4 万m3/h,年输气能力为3.15亿m3。试样的材料基本力学性能参数见表1,按照GB/T6398—2017《金属材料疲劳裂纹扩展速率试验方法》[12](以下简称“标准”),采用宽度W=50 mm,厚度B=12.5 mm,机加工缺口长度an=6 mm的标准紧凑拉伸CT试样,如图1所示。试样缺口通过线切割加工而成,预制的裂纹由热处理后再进行线加工而成。

表1 管材力学性能表Table 1 Mechanical properties of pipeline material

图1 标准CT紧凑试样Fig.1 Standard CT compact sample
2.2 试验过程
试验采用“标准”中推荐的U型夹具,在MTS电液伺服疲劳试验机上进行试验测试,如图2所示。利用MTS-810试验系统自动记录加载载荷及循环次数。试验所加载荷频率为10 Hz,波形为正弦波,应力比R=0.1。
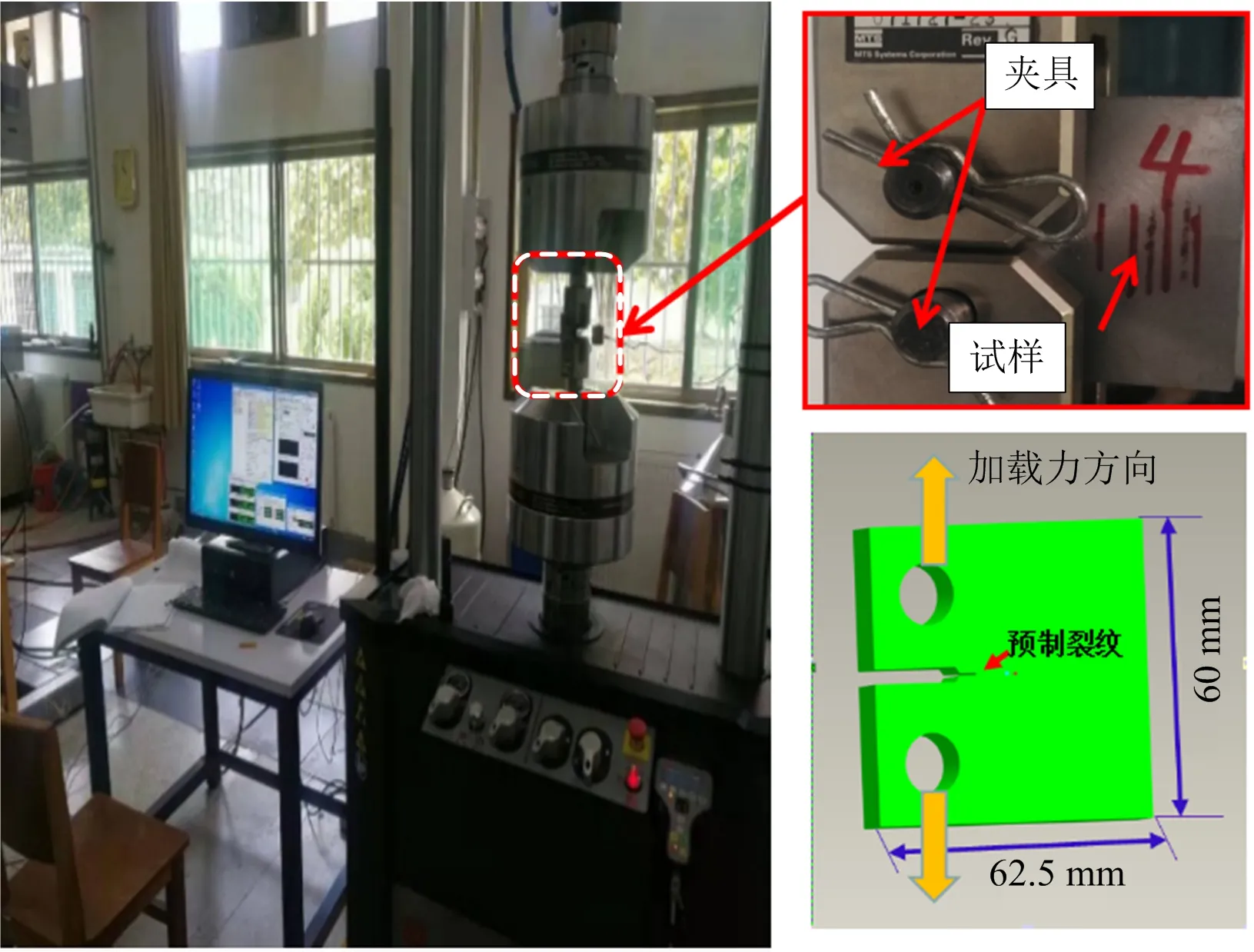
图2 MTS-810系统装置图及试样示意Fig.2 MTS-810 system device and sample schematic
具体试验过程如下:
1)按照“标准”中的相关规定计算得出各试件的预制力,并将其加载到试验系统预制出长度为9 mm的裂纹;
2)在室温、空气环境中,分别采用4种不同的载荷(14.4,19.53,22.32,25.11 kN)进行疲劳试验,试验过程中保持恒定的交变载荷幅值Δp。
3)利用高清数码相机拍照记录试件裂纹扩展过程,分析破坏形态;
4)分析处理试验系统所得数据、曲线和试验过程照片,得出结论。
2.3 试件破坏形态
试样随交变次数裂纹扩展图如图3所示。由图3可知,在交变应力作用下,试样疲劳破坏起始于预制裂纹的尖端缺口处,在循环次数较少时呈现出近似弹性的变形模式,但存在着塑性损伤累积效应;随着循环次数的增多,缺口处表现出明显的塑性变形,裂纹有一定的扩展;随着循环次数的继续增加,疲劳裂纹逐渐扩展,各试样之间表现出不同扩展路径,如图4所示,疲劳裂纹基本与最大主应力方向呈90°,断口表面存在明显的微坑和韧窝,符合I型裂纹的破坏特征。

图3 试样(4#)随交变次数裂纹扩展Fig.3 Crack growth of sample (No.4) with alternating times

图4 试样破坏形态Fig.4 Failure patterns of samples
3 结果与讨论
3.1 疲劳裂纹扩展分析
为获得da/dN数据,采用递增多项式对(ai,Ni)进行拟合,采用递增多项式拟合的4种载荷下的a-N曲线,如图5所示。

图5 裂纹长度a与循环次数N关系图Fig.5 Relationship between crack length a and cycle number N
通过计算不同应力下da/dN和应力强度因子ΔK,并对其取常用对数后,得到不同应力下lg(da/dN)-lg(ΔK)关系曲线,经过回归处理,结果表现为1条直线,其中,lg(C)为直线的截距;m为直线的斜率。通过分析直线的方程,就可确定da/dN与ΔK的关系[13-14]。如图6所示。
对图6各数据进行回归拟合即可得到Paris公式中的2个参数C和m,即可得到不同应力水平下疲劳裂纹扩展速率与应力强度因子之间的关系表达式,如下:
F=14.4 kN时:
da/dN=1.93×10-11(ΔK)2.754
(9)
F=19.53 kN时:
da/dN=2.53×10-10(ΔK)2.28
(10)
F=22.32 kN时:
da/dN=1.43×10-9(ΔK)2.21
(11)
F=25.11 kN时:
da/dN=1.18×10-9(ΔK)2.29
(12)
从各组试验结果发现,在低应力水平或低应力强度因子ΔK下,试样疲劳扩展速率较为缓慢,随着应力水平的增加,da/dN越来越大,当应力水平达到某一临界值时,裂纹扩展速率急剧增加,其低周疲劳寿命急剧下降。产生上述原因为:当裂纹扩展驱动力大于试样的裂纹扩展阻力时,预制裂纹尖端会张开和产生塑性区,当裂纹扩展驱动力增大到一定时,已大于材料的破坏强度,裂纹尖端张开位移急剧增大,导致裂纹尖端的塑性区急剧扩大,此时极易发生断裂。
3.2 疲劳裂纹扩展寿命计算
通过实验可得同一应力比不同应力强度因子下裂纹扩展速率Paris公式中的C和m值。选取《城镇设计燃气规范》(GB50028—2006)[15]中规定的常用燃气管道壁厚t=4 mm,外径d=150 mm作为计算分析对象,对于低压输送钢管,规定内压变化为0~1.5 MPa。计算分析时,假定初始裂纹长3.5 mm,深度为1 mm,裂纹长宽比a/b为1.75。
至此,只需改变现场工程实践管道输送燃气内压Δp和裂纹深度a0,利用理论的公式,可得管道上初始裂纹扩展至临界失稳尺寸的疲劳寿命。利用已得裂纹扩展规律,达到预测现场管道疲劳寿命的目的。
3.2.1 深度变化对疲劳寿命的影响规律
4种裂纹扩展速率的条件下,疲劳寿命N与裂纹深度的关系如图7所示,管道的疲劳寿命与裂纹深度的变化近似成线性关系。由图7可知,斜率的变化程度反映了应力强度因子对管道疲劳寿命下降的影响程度。在低应力水平或低ΔK下,管道疲劳寿命随裂纹深度的增加下降较为缓慢,能够较为明显地观测到寿命的变化。但是,随着应力水平的增加,裂纹扩展速率不断增大,管道的疲劳寿命急剧下降。
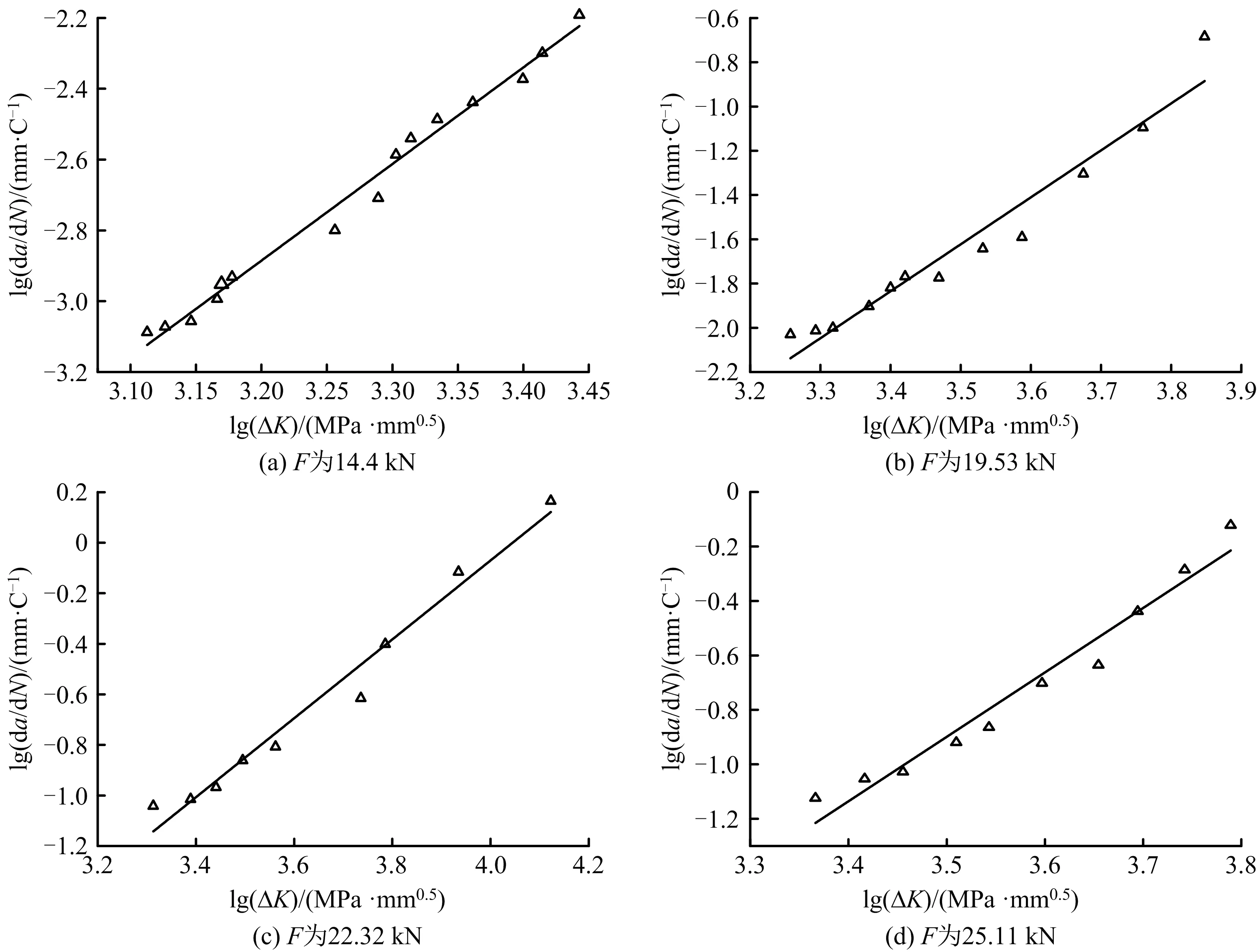
图6 裂纹扩展速率随应力强度因子的变化规律Fig.6 Variation laws of crack growth rate with stress intensity factor
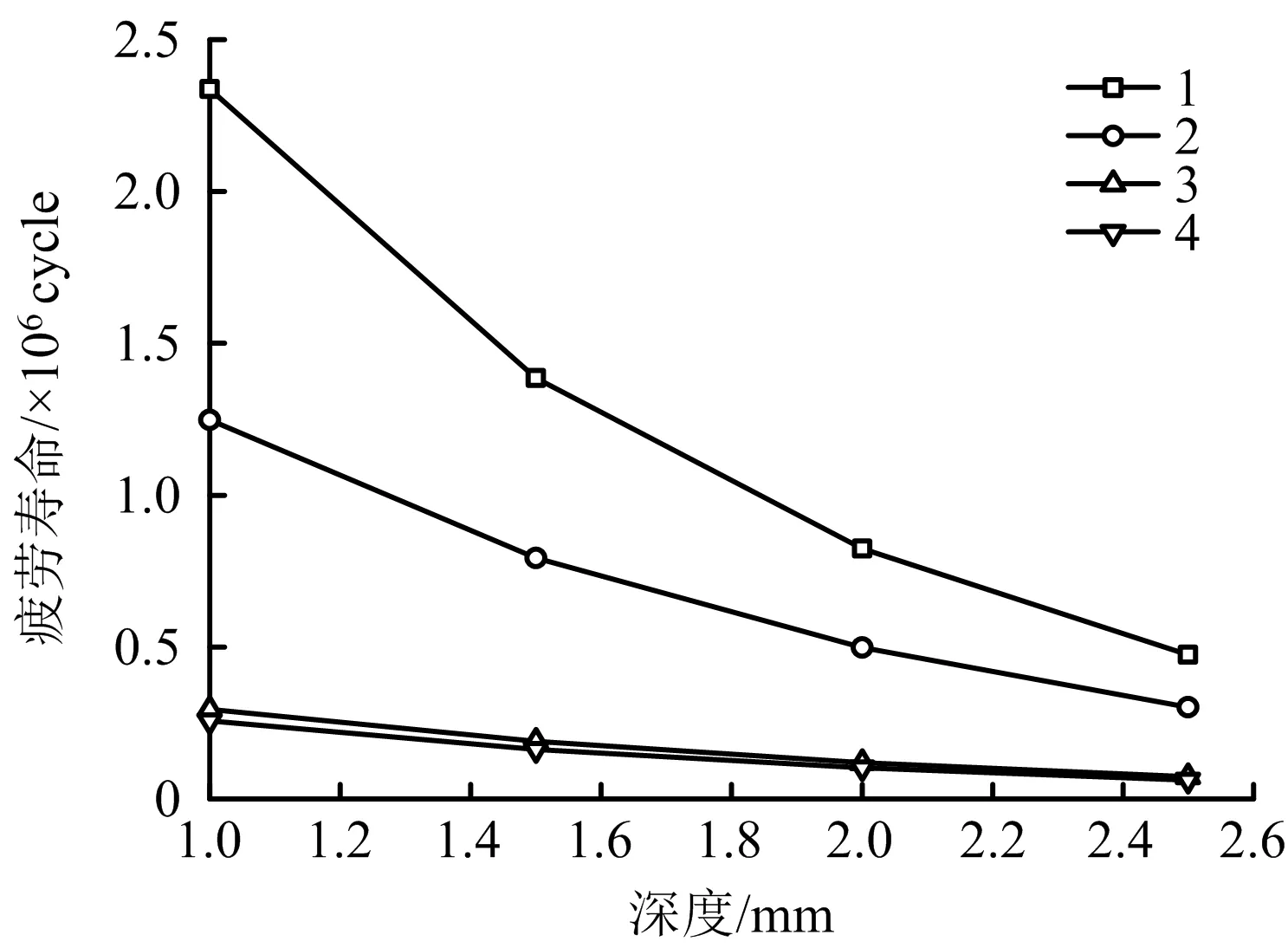
图7 疲劳寿命N随深度变化的影响规律Fig.7 Influence laws of fatigue life N with depth
在假定燃气管道内压幅值为1.5 MPa的条件下,在第1种和第2种扩展速率下,裂纹在深度上由1 mm扩展到2 mm,此时管道仍有较长的服务年限。而在第3种和第4种扩展速率条件下,当深度为2 mm时,疲劳寿命仅为102 370次,需要及时采取维护措施。
3.2.2 内压幅值对疲劳寿命的影响规律
4种裂纹扩展速率的条件下,疲劳寿命N与内压幅值的关系如图8所示,曲线近似为指数为负的幂函数。由图8可知,内压幅值变化对含初始裂纹的燃气管寿命更为敏感。疲劳寿命变化大致可以分为2个阶段,第Ⅰ阶段为安全阶段,第Ⅱ阶段为破坏阶段。考虑计算管道寿命时,有必要考虑一定安全系数,取安全系数为1.5,在第Ⅰ阶段内,4种裂纹扩展速率条件下管道至少工作寿命为31 a,满足30 a的设计服务年限。为此,应控制内压幅值,避免进入第Ⅱ阶段。

图8 疲劳寿命N随内压变化的影响规律Fig.8 Influence laws of fatigue life N with change of internal pressure
在假定燃气管道初始裂纹深度为2 mm的条件下,在第1种和第2种扩展速率条件下,当内压幅值达到3 MPa时,就要及时进行维护。而在第3种和第4种扩展速率条件下,内压幅值达到1.5 MPa,就需要及时补救。
通过对图7~8的分析和比较,可得到以下结论:
对于含缺陷的低压输送管,疲劳寿命对于内压幅值的变化Δp更为敏感,这就要求在日常生活中,输送燃气一定要保证内压变化保持稳定,尤其对于含初始缺陷的燃气管,内压幅值应当尽量保持在1.5 MPa以下。
4 结论
1)对于含初始缺陷的低压输送燃气管,内压幅值的变化Δp影响疲劳寿命更为明显,关系近似为指数为负的幂函数,内压变化幅值应当尽量保持在1.5 MPa以下。
2)管道的疲劳寿命与裂纹深度的变化近似成线性关系。对于第1种和第2种扩展速率,随着裂纹深度的变化,燃气管道疲劳寿命下降程度较慢,可以及时采取措施。而对于第3种和第4种扩展速率,燃气管疲劳寿命变化程度较大,当裂纹达到2 mm时,应及时采取维护等相应措施。

