基于龛深及其上覆土层稳定性的崩壁崩坍形成条件研究
马鹏飞,许文年,夏 栋,夏 露,严雨洁1,,邓羽松
(1.三峡大学 生物与制药学院,湖北 宜昌443002;2.三峡大学 三峡库区地质灾害教育部重点实验室,湖北 宜昌443002;3.三峡大学 三峡地区地质灾害与生态环境湖北省协同创新中心,湖北 宜昌443002;4.华中农业大学 资源与环境学院,湖北 武汉430070)
崩岗作为中国南方低缓丘陵山区特有的一种自然灾害,用来描述一种红壤区山坡土壤或花岗岩岩石风化壳地表在地貌地形(如坡向、坡形、高程)、地层组合、水力特性、干湿效应、重力、人类活动等影响因子耦合叠加下,不断地被剥离、崩坍(塌)、陷蚀、堆积后形成深切围椅状崩口崖壁地理实体的广泛存在的土侵蚀现象[1-4],其子系统包括集水坡面、崩壁、崩积堆、冲刷沟道及冲积扇[5]。崩岗是水土流失中极端的一种侵蚀状态,是沟谷侵蚀和生态系统退化的高级阶段,亦是土壤侵蚀的最高表现形式,有学者形象地视崩岗景观为“烂山”、“溃疡”、“劣地”[6-8]。崩壁是风化壳土体在重力与水力的作用下发生滑塌、倾倒等变化而产生的极不稳定的陡壁[9](坡度多>60°),是集水区与崩沟系统的交界面,是崩岗再次发生后续侵害的基础[5,10-11]。崩壁在坡面某处因地表径流侵蚀而内凹,其凹陷的区域就称为龛,龛的孕育与形成是崩岗形成的初级阶段[12-13],当龛出现并扩大后,其上覆红黏土层失去支撑,使崩壁处于欠稳定状态,才为崩壁崩塌及后退创造条件。
长期以来,国内学者一直致力于崩岗成因及其侵蚀规律的研究,并主要从地质地貌、坡向、植被覆盖、土壤理化特性(机械组成、分形特征、微结构、土水特征参量等)、抗蚀性、花岗岩不同层次岩土特性(包括抗剪强度、可塑性能、崩解特性、胀缩特质)与崩岗发育之间的联系等方面展开[8,14-16],且取得了较好的成就。可是在某些方面,诸如,有关崩壁几何因素与崩岗成因之间的关系及崩壁防治方法多为定性描述,定量模型的建立较为欠缺[9,17-18];其次,数值方法具有可重复性、直观性、数据容易提取等优点[19],但涉及崩岗侵蚀领域的研究多集中于监测或试验手段[20],缺乏严谨的数学力学理论基础,在数值研究方面鲜有探讨,难以清晰地揭示崩壁失稳滑移面的渐进扩展过程;再者,土层抗剪强度是土壤含水量的函数,可直接表达崩壁土体的稳定程度,故崩壁的稳定性系数可表示为土抗剪强度的泛函,然而将抗剪强度引入对崩岗稳定性的研究严重稀少[5],以至于无法定量地分析水分与崩壁崩坍之间的联系;最后,目前崩岗研究侧重于事后治理工作,但传统崩岗综合防治措施没有严谨的理论支撑,不仅治理工程周期长、成效低,有时反而会在一定程度上促使崩岗的发展,这恰恰增加了对预测预报崩岗土壤侵蚀及崩壁崩坍几率的需求[5,21-22]。野外调查证实[10],龛形态的变化(主要表现为其凹陷深度的增加)能有效反映崩岗发展强度的大小,对揭示崩壁溯源侵蚀规律有直接意义。然而在过去[23-24]对崩壁龛的研究多停留在对龛下定义、龛发育历程及其形成原因的描述等层面,对龛形态的演化进行多年测量统计的工作[10]少有报道。龛的发育程度与崩壁失稳崩塌之间的定性关系较明确,但对二者之间定量关系研究仍处空白,二者定量研究可作为崩岗成因机理研究、崩岗防治的理论基础,可用来预测预报崩壁崩落时机。为此,有必要建立崩壁—龛分析模型,在前人的既有成果基础上开展进一步地深入研究。
在天然状态下,当且仅当龛的发育规模(或龛深)足够大,崩壁才会发生明显的崩塌后退破坏[10];退一步讲,如龛深较小时,若崩岗壁各层次土壤含水量足够大是否也会触发明显崩坍呢?基于此,本文以湖北省咸宁市通城县内的一处崩壁剖面为范例,依托Abaqus软件平台,建立崩壁连同龛的有限元分析概念模型。采用对砂土层由外向内分级开挖的方式来模拟龛深的时空演变,计算触发该范例崩壁明显崩塌所需的龛临界深度值。通过设计9组正交有限元试验方案,改变算例的原始参数,对影响崩壁崩坍难易度的崩壁坡度、崩壁高度、龛高所占砂土层厚度的比例、水分含量进行了因素主次评价;针对正交试验得出的最优解(使崩壁处于最稳定状态的解析解),进一步寻找若干较小的龛深与引起崩壁崩坍所需的龛上覆土层最小含水量之间的定量关系,以期为崩岗失稳的预测提供数理依据。
1 研究区概况及数据处理
1.1 研究区概况
鄂东南通城县崩岗侵蚀区是湖北省崩岗集中分布的典型地区,其崩岗的发生规律在南方具有很好地示范性,因此选择该县境内五里社区为供试土样采集地。阜山北麓通城地区属北亚热带季风气候区,温暖湿润,年内降雨量时空分配不均,光照适中,四季分明,雨热同期,东南西三面环山,北面平坦,地势南高北低,海拔高程142 m,全县土地面积共计1 172 km2[25],土壤类型为红壤。多年平均气温约16.3℃,日最高气温39.7 ℃,极端最低气温-15.2 ℃,>10 ℃的积温为5 058℃,多年平均降水量1 550 mm,年平均径流深795 mm,无霜期260 d。据遥感显示,全县有大小崩岗1 102个,年土壤流失量达1.20×106t,占通城侵蚀总量的58.4%。在该地崩岗发生造成工民建筑、良田、湖库沟渠、交通路线等遭到严重损毁,导致较大经济损失。
本研究选取的崩壁仍处于发展状态,其剖面结构自上而下被划分为:表土层A(有机质和游离Fe2O3含量高,土粒细腻,偶有大颗粒石英,长石、云母已完全风化,厚0.5 m)、红土层B(土质均匀,土粒细腻紧实,长石、云母已完全风化,黏粒含量高,厚4.5 m)、砂土层C(高岭石含量高,有机质和游离Fe2O3含量低,胀缩性弱,原状土结构较松散,粒径较红黏土明显增大,由石英、半风化或未风化彻底的长石和云母构成,厚2.5 m)和未出露碎屑层D(保持花岗岩原生构造)。受燕山运动剧烈的南北向挤压力及地应力场等影响,鄂东南花岗岩土体内发育了多组节理和裂隙。尤其是垂直节理的强烈发育,利于崩壁崩坍发生[26],主要节理产状为320°∠77°,48°∠75°[12]。采样点处崩壁坡面平均倾角经勘察为70°。
差异性风化改造使崩壁形成独特的岩土分层结构,具有一定的土壤退化特性,不同层位性质(如矿物成分、孔隙度、力学强度、物质迁移、导水率)空间分异悬殊,使得各土层抗水流、抗侵、抗崩解、抗崩坍等能力差异较大。砂土层C 是崩壁崩塌的关键层次,它强度较低,崩解速率高且抗冲蚀能力极低,受水力影响较大,遇水弱化性极强。地表径流从集水坡面流下,在上层土体形成造崖层的小型瀑布,进而转化为瀑流,下部砂土体被不断淘蚀并剥落后极易形成溅蚀坑,进而扩大成侵蚀龛[4,23](见图1)。

图1 研究区崩壁侵蚀龛现场实景图片
崩壁坡体由龛上覆红黏土边坡SP1(由土层A 和土层B 构成)和砂质土边坡SP2(由土层C 和土层D构成)组合为复合边坡[27]。SP1土体抗冲蚀性较强,持水能力大易吸湿增重,当含水率较低时坚硬易开裂,强降雨期饱和度大时减压膨胀呈塑性[28]。SP2遇水易解体掉块,土壤结构稳定性小,其水稳性指数IPSP2≪IPSP1。因龛的存在,SP1易与下覆土层配合形成悬空面,同时上黏下砂的土层界面,岩土体充水时崩壁内力表现为“上重下轻、内重外轻(在同一高程内层的挤压应力和膨胀潜势能均大于坡面地表应力)[27]”,造成崩壁不稳而有向下向外崩落的趋势。
1.2 主要数据来源与处理
现实中尤其是夏季高温高湿环境下,经过若干次干湿效应(亦称干湿水平,命为Θ)交替变化,SP1土体因水分屡次进出,SP1土体的抗剪切强度τ值及其重量也随之改变。为了在数值计算时能反映这种现象,将现场采集的崩壁原装土样搬回实验室做不同程度的浸水或风干处理,共设置6种Θ。不同Θ 对应的崩壁各土层含水率ω通过铝盒法测定(见表1),各层次土体在不同含水率ω下的重度γ可由γ=ρdg(1+ω)求出,土壤干密度ρd 由环刀法标定(见表2),不同ω 下的黏聚力c、内摩擦角φ值通过应变控制式不排水剪切试验获取(如表3)。因碎屑层在地表以下采样很困难,其各种基本参数均无法通过试验获得,但考虑到碎屑层矿物成分风化较弱,相互结合较紧密,保持花岗岩原生纹理构造,碎屑层以下为球状风化花岗岩基岩层,故可将该层和其下的基岩归并为同一土层(命名为弱风化花岗岩土层,记作D*)以简化分析。崩壁塑性破坏区一般不会出现在地表以下,本研究仅关心龛上覆土层处于极限状态时的破坏区,因此土层D*的原始参数取值对崩壁整体研究意义不大,可假设其γ 和τ在各Θ 下为恒定值。又因碎屑层土粒的c和φ 值随ω 的变化又很微小,故认为土层D*的c和φ 在各种Θ下不变,其取值通过参数反演并依经验综合判断,最终确定分别恒取19.250 k Pa,38.140°,γ 值则列于表2。变形模量E 和泊桑比μ 则结合工程地质手册选用合理的数值。

表1 崩壁不同土层在不同干湿效应Θ 下的含水率ω

表2 崩壁不同土层的主要物理力学参数建议值

表3 崩壁不同土层的黏聚力c和内摩擦角φ
2 问题的提出、研究方法及分析模型
2.1 拟解决的问题
首先对相关概念进行阐释。随着龛在砂土层内沿水平方向凹陷深度d 的增加,其结果是启动龛上覆红黏土边坡SP1崩坍所需能量越来越小,因此必有一个龛深值致使SP1土层恰好发生大幅度崩坍(失稳),为便于叙述,将这个龛深值命名为龛临界(极限)深度D0(注:下标“0”非数字0,仅表示一个记号,下文可类似理解)。从另一角度试想,若龛深d<D0时,但SP1土层的含水率高于天然含水率ω*时崩壁尚处于稳定状态,设想继续增加SP1土层的含水率(如遇强暴雨),因SP1土层被通过裂(孔)隙入渗的雨水弱化导致其力学特性(τ 值)连续劣化,且红黏土吸湿增重,故也必有一个含水率值触发边坡SP1恰好崩落,将这个含水率值命为SP1的临界水分含量¯ω0(¯ω0>ω*)。
若在某T0时刻的前几天内没有遭遇明显降雨,温度也不太高(水分蒸发量可不计),则将T0时刻崩壁所处的状态命为天然状态(记为δ,对应Θ=4)。对于不同d 值与崩岗侵蚀(或崩壁稳定性)之间的关系,本研究关心两个广义问题。①对于长期处于δ状态的崩壁,d 为何值时崩壁会发生崩坍?龛在演变历程中,崩壁的破坏区随着d 的增加有何发展规律?②虽小于D0值的一系列d 值d1,d2,…,D0-1的 崩壁在ω*下未崩坍,但若虚拟增加崩壁土层的含水率ω 直到¯ω0时,崩壁可能会突然大体积解体崩塌。此问题旨在求出d1,d2,…,D0-1值下使龛上覆边坡SP1恰好形成崩坍时与d1,d2,…,D0-1相对应的¯ω0(¯ω0>ω*)。
2.2 拟采用的基本求解思路与方法
(1)问题1。将崩壁所有土层的ω 取为各自的ω*,随机取若干龛深d1,d2,…,d0-1,d0,d0+1,…,dn组成{dn},满足Δd=di-di-1=0.50 m(i=3,4,…,0,…,n)且d2=2.00 m。为模拟现实中龛的孕育是从坡面边缘开始的,限定d1值的计算(式(1))中龛的圆弧上切点是从红土层与砂土层的接触线与坡面的交点起算。随着砂土层被水蚀风化程度的增加(表现为d 值变大)龛向砂土层内部扩展的过程利用Abaqus软件接触对算法中的“生死”单元功能呈现(详见图2)。具体操作过程中,软件将欲开挖掉单元的刚度矩阵乘以一个无穷小因子,则单元荷载变为零,从而不对荷载向量生效[29]。主要计算分析步设置如下:在Initial初始分析步后添加Geostatic分析步,并规定允许的位移容限进行初始地应力平衡,计算崩壁在自身重力下的弹性变形和应力作为初始状态;之后在Geostatic步后插入n个静力通用Remove分析步r1,r2,…,r0-1,r0,r0+1,…,rn,分别开挖(“杀死”)图2的r1,r2,…,r0-1,r0,r0+1,…,rn区域,以实现龛深逐步增加的动态历程。当Abaqus/Standard提交作业后计算进行到某一开挖步r0时,塑性变形范围或屈服区从内部连通,就认为此时崩壁已崩塌,但分析步r0-1塑性区并未贯通,就认定分析步r0对应的龛深d0为龛的粗略临界深度。若计算进行到分析步rn结束时塑性区还未连通,则需在rn后插入一系列开挖分析步并重新试算;如r1结束后塑性区就已贯通,则需在r1前插入一系列开挖分析步试算,但此时龛末端圆弧须改为普通弧线,等差Δd须作相应减小。

式中:h——龛的高度(m);α——崩壁的平均坡度(°)。
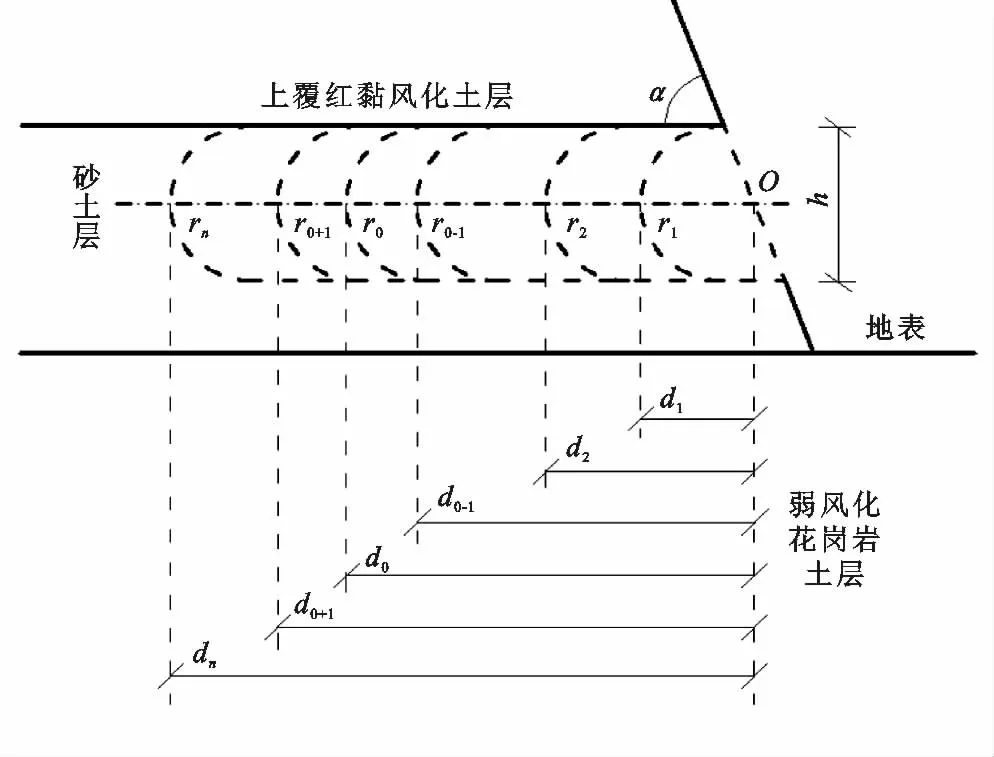
图2 分步挖除(杀死)动态过程模拟(生死单元)法示意图
为了提高D0的求解精度,设{dn}中d0的紧邻上一个龛深为d0-1,应用计算数学“二分法”的思想,取d⊕=(d0+d0-1)/2。在开挖步r0-1之后,分析步r0之前另插一个开挖步r⊕(对应d⊕),查看龛深为d⊕时塑性区是否连通,如是,在区间(d0-1,d⊕]用二分法重复上述步骤;否则在(d⊕,d0]上用二分法重复计算,直至绝对误差限(距离)ε=|d0-1-d⊕|或ε=|d⊕-d0|小于1.250 cm 时停止计算,由于“二分法”总是收敛的,此时对应的d⊕值就定为龛精确的临界深度D0。笔者将以上算法叫做思路1。
(2)问题2。在问题1求解终止后,为叙述方便,假设算出的D0为D0δ,预取小于D0δ的m 个d 值构成数列{dem},并任取尾项dem使其接近D0δ,且{dem}满足Δde1=dei-de(i-1)=0.50 m(i=6,7,…,m)。首项de1=0.00 m 且Δde2=de(i-1)-dei=-0.25 m(i=2,…,5)。之所以在{dem}中设2个不同的Δde,是由于现实中d 的目测值一般小于1.00 m,在[0.00,1.00]上适当加密龛深计算点更符合实际。当在{dem}中取某一值如1.00 m 时,在δ下崩壁未崩坍,但在雨水通过表土层下渗过程中红黏土层的ω 会逐渐增加,若ω 继续增大至某一值¯ω0时,崩壁塑性区刚好贯通而达到极限破坏状态。再人为预取若干含水率ω1,…,¯ω0-1,¯ω0,¯ω0+1,…,ωm组成新数列{ωm}。其中,等差Δω=ωi-ωi-1=0.50%(i=2,3,…,m),且ω1取比ω*稍大的任意值∀ω1。计算中令砂土层与土层D*的含水状态恒定在Θ=4(依据是:砂土层和红土层交界线附近入渗系数明显小于SP1土体的入渗系数,在崩壁剖面红土层偏下部存在一弱透水层[30],故在暴雨作用下SP2的含水量变化微小),只增加红黏土层的ω,直至¯ω0时崩壁崩坍,运用二分法求出与龛深为1.00 m 对应的临界含水率¯ω0(使允许误差限ε 在0.05%内)。对于{dem}中的每一个dei值按上述方法都能求出相应的¯ω0,将求解数据用平滑曲线连接,观察dei与¯ω0之间的变化趋势,并拟合出二者之间的函数关系式¯ω0(dei)。为计算方便,不计同一土层在各个方向上的含水率变化梯度gradω(x,y)。
2.3 有限元模型的建立
崩岗与一般滑坡类似[4],崩岗侵蚀关键因子分析可参考边坡、泥石流等较成熟的定量研究方法[31]。参照前人崩岗模拟的做法[32],本文作者视崩壁为一理想化的边坡,为节省计算资源,采用二维数值模拟技术,按照崩壁实际地层的分布情况,利用Abaqus建立如图3所示的崩壁崩坍前概化实体模型,为方便计算,将坡面简化为直线。固然崩岗崩壁不是无限长,但对于离开崩岗两端面相当远的剖面受端面的影响可不计,且由于崩壁形状沿一定长度范围内无明显起伏,故可按平面应变问题进行分析计算,上述简化方式可获得精度意义下的解答。考虑到边界效应会对计算精度带来影响,根据Saint-Venant原理,计算域范围取崩壁坡脚处向右延伸1倍崩壁高度H,坡顶左延1.5H,模型上下边界相隔2.0H。数值模型中大部采用4节点CPE4四边形完全积分等参网格单元形式,龛所占区域采用3节点CPE3三角常应变单元进行局部加密。岩土体采用经典莫尔—库伦弹塑性本构模型,边界条件为:模型底部二向约束,左右侧法向约束,地表及崩壁顶面无约束。
为进一步简化,结合实地踏勘情况,对崩壁-龛模型进行了如下必要的合理假定:①各土层等厚、连续、且为弹塑性各向同性均质体;②土层之间交界面单元的c和φ 相同,且崩壁各层既不互相脱离也不相对滑动;③将温度变化导致各土层力学性质的异变性归结为模量E 的差异[33],计算中不考虑裂隙的影响;④龛末端圆弧与红土层和砂土层的交界面相切(如图2);⑤不计地下泉水对崩岗底部的侵蚀作用。
3 计算结果与分析
3.1 龛的临界凹陷深度D 0 分析及因素敏感性评价
3.1.1 “开挖模拟法”数值算例、D0分析 以1.1节中所描述的处于δ(Θ 为4)下的崩壁剖面(几何参量为:H 为7.5 m,α为70°,h为2.0 m)为例,阐明利用“开挖模拟法”求D0的明细。崩壁岩土体的破坏区范围及位移随着d 的增加也随之改变,通过观察不同d下崩壁塑性屈服区的贯通过程图及位移等值云,可了解砂土层被淘空到一定进深时崩壁崩坍面的位置及土体单元破坏后的状态。

图3 崩壁连同龛二维整体模型及网格剖分
等效塑性应变与屈服区分布情况随着d 增加产生动态变化,塑性区与屈服区的发展变化情况基本同步。由Abaqus等值云得知,在龛形成过程中,土体单元首先在崩壁坡脚出现剪应变集中;当d 发展到3.50 m 时,随d 的增大,在后缘(即坡顶)开始出现以拉张为主的屈服破坏区;当砂土层被水蚀至4.00 m,后缘屈服区斜向下延伸,同时坡脚屈服区也在向上扩展,两部分屈服区连通直至形成贯通带,表明此时控制性结构面已逐步贯通,崩壁已达到临界破坏状态,龛上覆土体崩坍启动,崩坍后的产物将堆积在坡脚成为崩积堆(由崩坍后的变形网格图可知)。综合此时的应力云,崩壁顶部全是拉裂破坏区,意味着在野外会加速垂直纵张裂隙的产生,而坡脚形成压剪破坏区,龛末端位置处因砂土层被开孔受到扰动,出现极大的孔边Mises应力集中,使得圆孔附近的应力与变形状态完全改观,这一切共同促使崩壁快速形成滑移式崩坍面。同时结合计算云图也能较清晰地评判出崩坍临界滑裂面出现的大体位置(由于1个在滑动面两侧附近,且连续贯通的局部屈服破坏单元集合中必然存在一个滑动面[34],故可认为等值云中塑性滑带的中弧线即为滑裂面出现位置)和形状(呈直线)。
由以上结果可理解崩壁崩落机制:坡度较大的崩壁地形陡峭,为形成崩塌奠定了基础。砂土层风化松散,Mise应力集中,发生压剪破坏,加之跌水作用下易坍塌形成龛,不利于崩壁稳定的结构面。在边坡SP1自身重力和外营力作用下,裂隙易扩张贯通,崩塌受外倾结构面控制,红黏土体重心前移,导致锁固端逐渐破坏,使临空土体脱离母质土而坠落。
上述计算过程是按数列{dn}的项数n 取7进行的,但在开挖步r7之前的分析步r6迭代进行到t=0.959 9时,有限元迭代计算已不收敛,即崩坍面特征点位移有无限增长趋势,而Remove步r5迭代结束时屈服区未贯通,说明龛深极限值D0不大于r6对应的龛深d6=4.00 m,故考虑在d∈(3.50,4.00]上反复运用“二分法”查看开挖到区间中点的龛深d⊕时对应的屈服区是否贯通。逐步锁定精确值D0所在的区间,直到搜索出满足研究需求精度ε的D0时停止计算,最终求出该算例龛的D0值为3.68 m(为偏保守预测D0,此处四舍五入时逢五不进一)。
为更准确地剖析d 对龛上覆危岩体稳定性的影响程度,凡{d7}中已有的d 值以及用“二分法”求解过程中牵涉到的d 值,笔者对每一d 值都单独建模,应用有限元强度折减法计算相对应的崩壁稳定性系数Fs,其结果汇总于表4。当d 为3.688 m 时Fs→1(崩壁到达极限状态),从而检验了“生死单元法”求解D0的科学合理性。将表4中数据点在坐标纸中描点发现,Fs与d 之间服从很好的线性负相关规律,采用最小二乘法得到二者之间存在形如Fs=2.043 3-0.279 2 d 的拟合表达式,若另Fs=1.000 可得出d=3.737 m,取D0=3.73 m,与上述得出的3.68 m 比较接近。这里须要指出,现实中砂土层几乎不可能被掏蚀如此深才崩坍,而是强降雨时边被掏空,在下次阴雨连绵时边形成崩坍,崩坍后d 趋于零,砂土层重新被掏蚀。由此看来,D0≈3.70 m 似乎与实际有出入,但以上计算是在未考虑降雨条件(即自始至终都处于δ状态)下分析的。

表4 崩壁的Fs 与龛凹陷深度d 的关系
3.1.2 影响崩壁崩坍或崩岗侵蚀的因素主次分析 正交试验设计是一种可以研究多因素多水平条件的重要设计方法,可挑选少数具有代表性的组合处理进行试验,具有均衡分散性(在空间直角坐标系上均衡排列,不偏不倚)、综合可比性等优点[35]。本文在研究不同d 与崩壁崩坍的关系及其敏感性因素时,遵循“尽量少选因素和水平、考虑对试验指标影响大的因素、在不增加试验次数前提下,可多选因素少选水平”的原则,经全面考虑,最终确定H,α,h 与砂土层厚度之比(命为h^)及Θ作为本正交试验的4个试验因素,依次以A,B,C,D 表示。通过多次野外调研和地质分析成果知,δ状态下,通城五里社区H 一般集中在7.0~9.0 m,启动崩壁直线状崩坍失稳所需的α约在60~80°(当α<60°,崩壁失稳时产生圆弧状滑裂面,本研究不考虑此情形),h^的目测值一般在0.52~0.80,并将供试土样通过浸水处理使Θ 控制在合理范围内。选取的试验因素水平(表5),研究因素A 时假设各土层厚度随H 改变按原各土层厚度之比均匀变化(如H为8.5 m 时,表土层厚为(0.5/7.5)×8.5 m。
因上述各因素的水平数都相等、因素间交互作用均可忽略且易量化,满足选用4因素3水平标准正交表L9(34)进行设计的基本条件,正交试验方案如表6。在表6中9种试验条件下,根据“开挖模拟法”,D0的计算值统计于表7。可以看出,在选定的正交组合范围内,使崩壁恰好形成崩坍的D0在区间[0.005,5.172]内变化,在δ 状态及风干或高温失水状态(Θ为3)下D0较大,但当龛上覆土层略微增湿(Θ 为5)时,D0迅速减小。
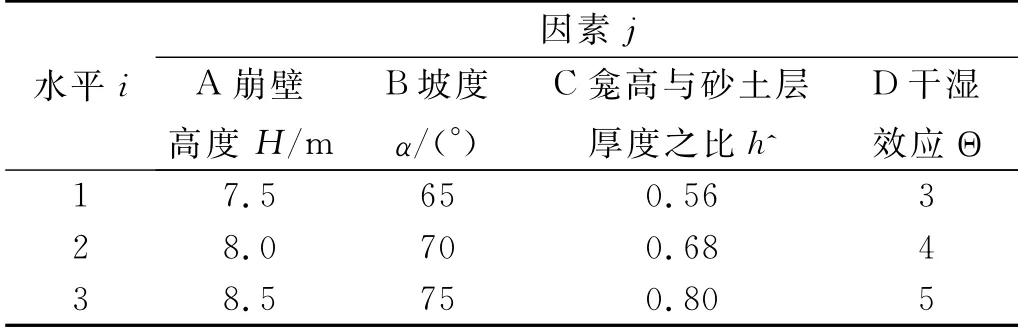
表5 试验因素水平表

表6 正交试验方案

表7 各正交有限元方案下龛深极限值D 0 的计算值汇总
处理正交试验结果一般通过R 法来综合评判因素的主次和最优组合,用R 法进行数据分析直观形象、简单易行。一般地,命Yji(j=A,B,C,D,i=1,2,3)为第j 因素i 水平所对应的试验指标(本文即指D0)之和,¯yji为Yji的平均值。¯yji的大小反映了因素j的i水平对试验指标的影响程度,据此可判断j因素的优水平,各因素优水平的组合即最优组合。命Rj为第j 因素的极差,其计算式见式(2),Rj表征了第j因素水平变动时试验指标的变动幅度,Rj越大,说明该因素对试验指标的影响越大,因此也就越重要。Rj最大的因素可认为是最主要的因素,反之是较次要的因素,于是依据Rj的大小可以进行因素敏感性分析。分别对表7中9组试验D0的求解值进行R 法计算和判断(如表8)。
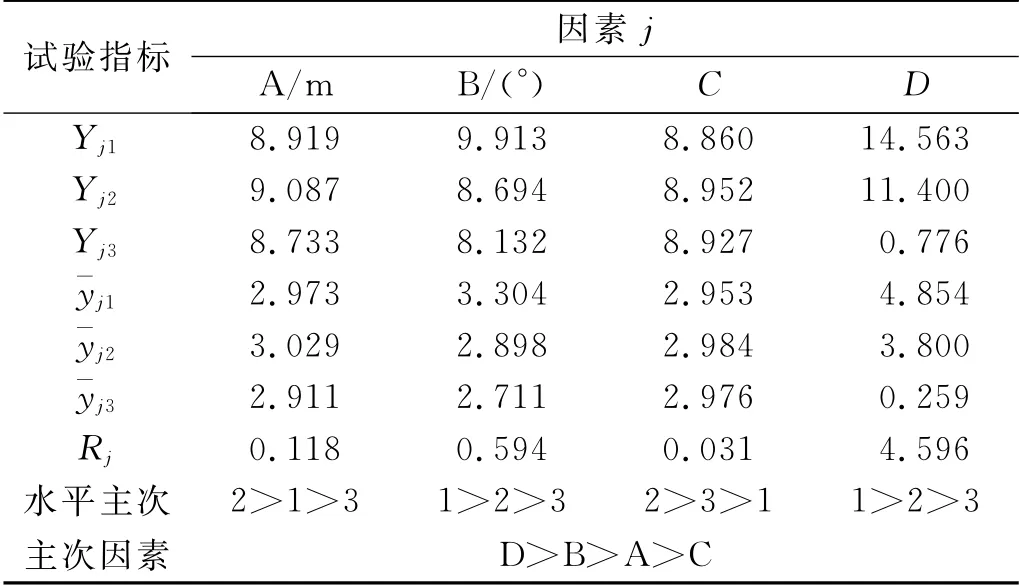
表8 多因素敏感性R 法分析结果
为更直观明了地揭示各试验指标Yji随各因素水平i的变化规律,现以i为横轴变量,Yji为纵坐标,绘制因素与指标趋势图(参见图4)。

通过比较各因素的极差Rj可以得出,4因素对试验指标D0的影响程度由大到小依次为D,B,A,C。Θ的变动造成崩壁稳定性受龛深d 的影响程度远大于其他因素,是最显著的影响因素,而Θ 明显增加往往是由于雨水入渗引起的,故崩壁崩塌多发生在集中强降雨期;α对D0也有较大的影响,H 的影响程度较小,而h^的变动对D0影响最小或者说几乎无影响。从主次水平分析,崩壁土体含水量和坡度越小,龛上覆土边坡SP1稳定性受d 的影响也越小,这是符合常理的;但H 和h^却存在这样的一个临界值(奇异点),使崩壁启动崩坍所需d 的最小值最大(见图4)。究其可能原因,当因素C 取值较小(h^小于0.68)时,虽然龛的体积较小,但龛进深最大处孔端Mises应力集中较大且占主导地位,导致边坡SP1稳定性降低,致使崩壁明显崩坍的D0相对较小,试想若命h^→0,则龛的存在相当于一细微裂纹,根据Griffith 强度理论,材料的破坏往往始于裂缝端,而崩壁土体受力后使裂纹尖端附近应力明显升高,这对龛上覆土体强度和稳定性极为不利;当h^达到0.68(即因素C 的2水平)时,孔端Mises应力减小,D0达到极大值;当h^继续增大,虽Mise应力集中现象继续减弱,但此时龛体积较大(龛上部临空面相对零势面的重力势增大)且居主控地位,换言之,龛体积的增大引起D0的减小值掩盖了Mise应力效应减弱引起D0的增大值,故D0反而减小。根据常识H 越大就越不稳定,但模拟试验结果表明,H 也存在一个使崩壁稳定性受龛深d 影响最小的临界值,笔者认为当H 增大时,砂土层的厚度也在增大,在h^一定的条件下,从而h 也在增加,可见研究因素A 时不能单纯从崩壁高度角度解释,还应考虑h变化导致Mise应力效应变化对D0的综合影响。综上所以,因D0(或¯yji)越大崩壁崩坍的概率就越小,故四因素优水平的组合便是本试验的最优组合A2B1C2D1,即崩壁最稳定状态。若命组合A2B1C2为最稳定条件IF,可以计算,在同时满足条件IF和崩壁Θ 为3的附加约束条件下,D0的理论值为5.295 m。
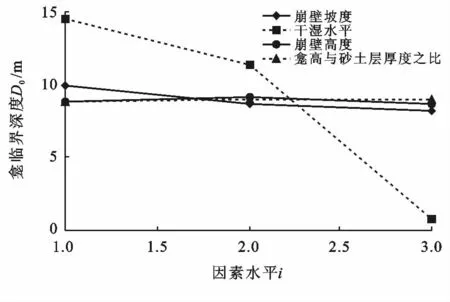
图4 因素水平与龛侵蚀临界深度趋势间的关系
3.2 触发崩壁崩坍的临界水分含量分析
研究问题2需用到红黏土层的c,φ 值与土含水量ω 之间的映射关系,由于只对很有限的6种Θ 下土层的抗剪强度τ值进行了实测(详见表3),仍无法满足科研需求。若用Excel表格拟合c,φ 与ω 之间的算子关系,不仅拟合的函数式有时光滑度较差(不能保证二阶导数连续),甚至在某自变量取值区间上目标值与真实值偏差较大,故在浸水试验有效数据基础上,可采取插值法手算,将有限的离散实测值变换为一连续的能描述c,φ 值与水分含量ω 之间关系的定量表达式,这样任取一较高的ω 值带入表达式求出对应的τ 值,并将其植入ABAQUS软件中便可模拟龛上覆土层吸水连续软化的真实状态。
因崩壁剖面各土层的ω 随时间空间改变而改变,而本文仅对通城县某一地理坐标的崩壁展开研究,加上影响崩壁崩坍因素的复杂性与不确定性,成果未必很好地适用其它地域的崩壁,故若将表土层和红土层在6种Θ 下的ω 用式(3)转化为各自的饱和度Sr显得更有实际意义,换言之,问题2的着落点转移到探索触发龛上覆红黏土崩塌所需的临界(最小)饱和度S*r0在什么范围内,似乎价值更大。为此,命表土层A和红土层B的饱和度分别为SrA,SrB,当雨水下渗到SP1土层时,在同一Θ 下SrA与SrB并不等,在求解问题2时是以SrA为准还是以SrB为准呢?注意到表1中红土层与表土层在同一Θ 下的ω 差别不算大(故猜测Sr也差别不大),可对两土层的饱和度取平均进行简化处理,命土层A 和土层B 按土层厚度加权的平均(或整体)饱和度为S*r(按公式(4)计算),计算结果如表9所示。为节省篇幅,文中仅以条件IF(H 为8.0 m,α为65°,h^为0.68)为例分析问题2。在条件IF下,当崩壁处在δ状态时,应用“开挖模拟法”得出D0δ(为避免前后混淆,将此处的D0以符号D0δ代替)为4.119 m,固定若干小于D0δ的龛内蚀深度dei,探索在降雨天气下SP1土层吸湿增重时的S*r增加到何值时崩壁突然启动大幅度崩坍。

式中:n——孔隙率(%);ρw(取为1 g/cm3)——纯水在4℃的密度;hA,hB——表土层和红土层的厚度(m)。

表9 龛上覆红黏土层的平均饱和度S*r 与Θ 的关系 %
下面以强度指标c和φ 值为因变量,红黏土层的S*r为自变量,求4个简单插值多项式近似替换表3。为避免舍入误差积累带来的病态问题,在进行插值计算时至少保留小数点后五位。由于只研究龛上覆土边坡吸湿增重过程中饱和度的变动对崩壁崩塌的影响,并不考虑自然蒸干过程中水分含量降低对崩壁稳定性的影响,故而忽略Θ 为1,2的情况,但为保证可靠度,保留Θ为3的情形,并取S*r3=0.529 00,…,S*r6=0.950 69为插值节点。对Θ 为3~6下的S*r与表3中相应的表土层粘聚力cA进行3次拉格朗日插值(公式(5)),同理,得出红土层黏聚力cB与S*r的3次Langrange插值多项式(式6)。从表3 可知cA应为S*r的减函数,但对式(5)求一阶导发现cA′(S*r5)大于0(≈13.615),在插值点S*r5附近的邻域δ(S*r5)内及区间(S*r5,S*r6)上式(5)严重失真。通过进一步求导得出cA′(S*r4)≈-127.3,并观察到在区间[S*r5,S*r6]上cA变化很小,故可另cA′(S*r6)=0作为第一类边界条件,在区间[S*r4,S*r6]上进行三次分段样条插值以保证所求分段多项式二阶导数连续可微,结果见式(7),可验证,式(7)具有很好的适用性。用类似方法得出cB与S*r的样条插值函数式(8)。对Θ为3到6下的S*r与表3中的表土层内摩擦角φA 进行3次牛顿插值(式(9)),同理,得出φB 与S*r的3次Newton插值多项式(式10)。公式(9)和(10)的精度能得到满足本文近似程度要求的结果,无需再进行样条插值,在不同的S*r下SP1土层的容重γ按式子(11)计算。至此,有了公式(7)—(11)就可以在[S*r3,S*r6]上∀S*r,求出其对应的所有计算参数,从而可分析该饱和度下崩壁当前的稳定程度或崩坍的几率。下面将计算数列{dem}中各数项dei对应的使SP1崩坍的临界饱和度S*r0。



鉴于前文算出的D0δ为4.119 m,故取{dem}的项数m=11比较理想,令尾项de11为4.00 m 以使其靠近D0δ。求解方法沿用求解问题2的思路2,只是将{ωn}换成S*r组成的数列。但判断崩壁崩坍(失稳)的标准不是沿用“单元生死法”塑性区是否贯通,而是利用有限元强度折减法,计算某一龛深dei(i=1,…,11)下的崩壁在红黏土取不同饱和度S*r时的Fs,若某次试取的S*r使Fs接近1,则采用“二分法”思想,缩小S*r的取值范围继续试算,直至试取的S*r使Fs无限逼近于1且误差限不超过0.05%,则认为该龛深度dei下的崩壁恰好形成崩坍,此时的S*r即为所求的临界饱和度S*r0。限于篇幅,表10只给出了计算结果。命(S*r0-S*r4)为边坡SP1相对天然饱和度S*r4的增量临界饱和度ΔS*r0,ΔS*r0>0对应红黏土降雨期吸水软化,ΔS*r0<0对应红黏土水分蒸发。为更准确地发现自然规律,现利用表10中的数据点以及之前算出的数据点(4.119,67.113)和(5.295,52.900),绘制条件IF 下龛上覆土层的平均临界饱和度增量ΔS*r0与dei的拟合关系曲线,结果如图5所示。

图5 龛上覆土层ΔS*r0随dei的变化规律(命为崩坍预测迹线)

表10 {de11}中龛深度dei与龛上覆边坡土层S*r0的映射关系
据任兵芳等[10]对龛形态资料的记载:通城县五里镇和程凤村龛深观测值分别在0.02~0.45 m 和0.20~1.00 m 范围内,由于H 及h 对崩壁崩坍事件发生的影响程度相比d 而言很小,故可近似认为致使通城崩壁形成崩坍的S*r0与H 和h 无关,也就能使得以采样点处的崩壁为研究对象所得的结论可近似适用于通城县其它地理坐标类似地质环境下的崩壁。将龛深观测值代入图5 中经验拟合公式ΔS*r0≈16.577-0.957 2dei-0.846 9d2ei,可得到五里镇和程凤村α在65°附近的崩壁,其临界饱和度预测值的区间范围分别为[83.088%,83.671%]和[81.886%,83.465%]。对于非65°的崩壁可按思路2提供的算法重新推导对应坡度下的临界饱和度经验公式,并可重新对S*r0的大致范围进行估算。
4 讨论与结论
4.1 结果讨论
4.1.1 对问题1与问题2的几点反思及讨论 查看图5中曲线的走势,龛深与ΔS*r0近似满足二次函数变化规律,且显著负相关(其拟合决定系数R2为0.980,表明龛深与ΔS*r0之间的函数关系式真实存在)。由此可推出龛越发育(即dei越大)崩岗发育越快(图5中曲线斜率在增长,即SP1的饱和度S*r与致使崩壁崩坍灾害发生所需的极限值S*r0之间差值的绝对值的减小速率在增加),这与任兵芳[10]等人研究结果一致。
设某地按时间先后顺序遭遇N 次降雨,每次降雨总量依次命为Q1,Q2,…,QN。既然龛的形成与扩大由降雨或爆流引起[36-37],而崩岗壁的大量崩塌也是在强暴雨期土体饱和度增加、增重和软化等一系列过程后发生的[24],那么崩壁在经历一次降雨过后,究竟是发生龛的扩大还是启动崩壁崩坍呢?问题2的解答提供了一种有理论支撑的回答:若一次降雨过程使得边坡SP1的饱和度S*r达到或超过对应此龛深的S*r0,它将发生崩坍;反之,倘若一次降雨量Qi(i<N)没有使得SP1的S*r达到S*r0,则它将促使龛的萌芽或d 值增加(崩壁不会启动明显崩塌,但可能会有坡面浅层土体局部流滑)。而龛扩大的结果使得崩壁的Fs降低,就意味着下次促使崩塌的临界雨量Q(i+1)0(或临界饱和度)小于之前与使龛扩大相对应的临界雨量Qi0(Qi<Qi0),若Qi+1还没达到Q(i+1)0,则结果是d 继续加大,Fs继续下降。如此反复,直到d 达到某一较大值,相应的临界雨量达到一较小值,此时SP1也许稍微吸水(雨量不大)就会发生崩塌。这种思考提醒我们,因龛形成的危害小于崩壁崩塌的危害,若某崩壁龛的形态用肉眼能明显识别,那采用填充龛的方式就意味着提高了SP1的极限饱和度(或雨量阈值),间接降低了其崩坍破坏的可能性。
在强降雨或持续中小雨环境下,命崩壁崩坍为事件1,龛的孕育或龛深d 增加为事件2,事件1与事件2发生的概率分别为P1,P2。若假设一场强雨过后,事件1与事件2对立,且事件1与事件2发生足够长时间后崩壁处于δ(即含水状态恢复到Θ 为4),则每逢降雨时事件1或事件2的发生与否,完全取决于相应的龛深下降雨后红黏土体的S*r是否从天然饱和度S*r4增加到临界值S*r0。在侵蚀龛未出现前,强降雨时因雨水入渗量及红黏土吸水有限,S*r一般达不到de1=0.00 m 对应的临界值0.853 29,P1几乎为0,P2几乎为1,换言之,崩壁只有先出现龛等微地貌再崩坍。若下次雨强还未使红黏土壤的饱和度达到相应龛深下的临界值(此临界值小于龛未出现前的饱和度临界值),则事件2发生,d 加大。d 加大的结果是S*r0越来越小,且减小速率也在增加(对图5中的预测曲线拟合式求导便可知),这意味着以后的降雨中P1越来越大,P2越来越小,即崩壁崩坍的几率快速增大,直到某一次降雨使事件1 发生,发生的结果是SP1崩坍后龛深重新归零。重复上述步骤,如此循环不息,最终结果是致使崩岗进一步发育,这与任兵芳等[10]的论断“龛的不断形成(对应龛深增加)致使溯源侵蚀(对应崩壁稳定性降低直到崩坍形成,进而龛消失)最终导致了崩岗发育”相吻合。
以上分析在一定程度上缓解了问题1中计算的D0可达3.50~5.30 m 的矛盾,而如此深的龛在现实中是找不到的。问题1 的解答是在一种长期处于δ状态或(半)干旱状态(Θ 为3)的理想状态下分析的,而现实中崩壁土体一般是处于干旱—δ 状态—近饱和交替变化的环境,崩岗发育的过程也是崩壁边形成龛边经历崩坍的过程,故现实中所看到的龛深一般较小(属0.3~0.6m 范围)。从广义问题1 的研究分支—正交试验结果来看:当SP1的含水率ω 从ω*开始增加(Θ由4变到5)时,D0明显变小,即崩壁土体稍一湿润就可能引发崩坍破坏,这符合崩壁崩塌多发生在接连降雨期的一般事实;据图4,坡度与崩壁高度对崩壁稳定性的敏感性程度相比,明显是前者高于后者,这与季翔等[20]研究结果(崩岗侵蚀沟外扩主要受坡度的影响,坡面高度的规律性较低)相容。综合表7和图4可知,D0与土体含水状态密切相关,这也解释了崩壁常出现阴雨连绵时大量崩坍的特征最为重要的原因。显然,做好排水措施,减少集雨面积以减少雨水的下渗对稳定崩壁有重要意义。
总而言之,若没有前几次降雨在崩壁土体中使龛规模扩充的累积效应,一次降雨后红黏土层平均饱和度S*r很难达到无龛崩壁启动崩坍所需要的最小饱和度。伴随着降雨持时的增加或降雨间隔较短时,S*r的实时值S*r(t)与S*r0的差值有所减小,而崩壁土体中在一次降雨前初始含水量的多少,决定该次降雨时饱和度所能到达的峰值,该峰值与临界饱和度的相对大小决定了崩坍的发生与否。因此,崩岗形成与前期土体含水量相关,前期降雨在红黏土体中的水分累积效应对崩岗的发育起到重要作用,那么阴雨连绵时(即使雨强不太大)SP1土层饱和度的积累(量变)很可能会引起崩壁失稳(质变),这与王彦华[38]等观点(若没有前期降雨在土体中的累积效应,一次降雨的湿润前锋很难达到崩岗所需要的临界深度,当前降雨之前坡体中的含水量决定当前降雨的湿润前锋深度,是影响坡体稳定性的重要因素)非常一致。综上所述,前期降雨在崩壁体内具有累积效应,一方面使砂土层剥落并退去后形成龛,另一方面增加当前较深层土体的饱和度,减小抗剪强度,增加红黏土容重并产生动水压力,改变了崩壁的极限平衡状态,造成了崩壁失稳及崩岗的发育与发展。
4.1.2 崩岗治理新思路 对数值结果的分析,可启迪我们转换崩岗治理技术:应依据龛深值及龛上覆土层的增量饱和度ΔS*r双重指标对每个崩壁的稳定态势进行实时预测预警,以对出现的龛能及时进行综合处置,如对龛进行清除或用高聚物胶凝材料填充;对龛上覆临空欠稳定土体可采取柱支撑、网拦挡、石灰土加固等联合措施,并可结合实际制订崩坍应急预案,唯有如此才能有效遏制崩岗的后续侵害。对于崩岗严重区段,在处理龛的同时也可对崩壁其他要素采取一定措施如:对崩壁斜坡面补栽植物以截流,并可配合修建谷坊、拦砂坝等措施,必要时对坡顶裂隙,可采取封闭、埋置拥有一定抗拉强度的三维复合土工格栅,以最大化降低崩岗灾害的风险。
在崩岗防治工作中,实时预测其崩坍发生与否方法如下:对某次降雨后某t1时刻崩壁(α 为65°)的d进行人工量测,将量测值带入崩坍预警公式ΔS*r0≈16.577-0.957 2dei-0.846 9d2ei,得到t1时刻的临界饱和度预测值S*r0|t=t1。对土层A 和土层B分别插入湿度传感器进行ω 的实时监控,利用式(3)将ω 的监测值换算为饱和度实时监测值,将土层A 和土层B的饱和度实时监测值按厚度加权平均得到S*r|t=t1,若S*r|t=t1接近于S*r0|t=t1,则崩壁在t1时刻有崩塌失稳的迹象,必须对龛及时补救以防患于未然。
4.2 结论与未解决的问题
基于ABAQUS程序及数学近似处理思想,建立有较强预测和适应能力的崩壁—龛数值模型,在此基础上提出了与龛演化相仿的“开挖模拟法”及崩壁稳定性的定量分析方法。研究了通城县龛深对其上覆红黏土体稳定性的影响,并探索了一系列较小的龛深与导致崩壁崩坍时红黏土层所理应具备的最小(极限)饱和度之间的定量关系式,且试算结果良好,得出几点重要认识如下:
(1)崩岗崩壁坡度足够大时,潜在崩坍面呈直线或折线状,崩壁后缘形成拉张破坏区,易产生垂直拉裂隙。崩岗形成流程为:崩壁陡坡形成—下部土体被水蚀掉块—龛形成—红黏土层临空—解体崩落—堆积坡脚—崩岗产生。
(2)龛的形态对其上覆红黏土层稳定性的影响主要表现为深度增加对其的不利影响。崩壁在未降雨工况下一般是自稳定的,只有龛深达到一很大值时,才会启动崩坍;而龛上覆土层含水量从天然值开始增加时,龛临界深度骤减。
(3)崩壁高度H,坡度α,龛高与砂土层厚度之比h^,饱和度相对天然饱和度的增量ΔS*r的变化均会改变龛深对崩壁崩坍概率的影响程度,四因素的敏感性由大到小依次排列为:ΔS*r,α,H,h^,且ΔS*r的影响权重远大于其他各因素。在所设计的试验因素一定范围内,H 与h^的变动对红黏土层稳定性的影响非常小,这也揭示了在预测或计算崩壁的稳定性系数时,可以忽略掉H 对计算结果的影响。换言之,可以只根据崩岗的坡度和含水量来预报崩壁当前的稳定程度。依照感性认识,对于未出现龛的崩壁,H 越大越不稳定,但龛出现后,存在一临界高度H0使崩壁最不易崩坍,当H>H0时,此认识才能精确成立。
(4)抗剪强度在风干和増湿阶段明显不同,插值变换公式具有较精确解析解的性质,故可根据不同土壤含水量通过插值函数式预测土体抗剪强度,进而计算崩壁安全系数,从而为评估崩壁稳定性铺垫道路。
(5)一场暴雨后崩壁失稳与否,由降雨量是否达到使红黏土层的平均饱和度达到极限值的门槛值决定,而崩壁后退是由崩坍引起的,故可进一步得知,降雨量越大崩壁后退就越发明显。龛深与使具有这一龛深的崩壁恰好崩坍所需的龛上覆土体最小含水量之间呈二次函数递减趋势。
(6)结合有限元理论计算值,利用崩壁崩坍预测拟合公式ΔS*r0≈16.577-0.957 2dei-0.846 9d2ei,对促使通城崩壁剖面形成崩坍的临界(极限)饱和度范围进行了合理预测,其结果具有一定的参考意义。
风干阶段崩岗岩土体的强度主要受裂隙性控制,当红黏土体含水率极低时也会引起土强度降低,尤其是粘聚力减小较多,从而崩壁稳定性也会受到影响,故红黏土边坡饱和度处于低水平时龛的存在及裂隙的伸展与崩壁稳定性的关系尚待进一步深入研究,从而扩充成果的崩坍预测范围。本文也未能解决裂隙主控结构面的存在对崩壁崩坍的影响,但考虑到龛上覆临空土层可看做叠合构成的悬臂梁,梁的一端固定另一端自由的模式,因此龛深对红黏土稳定性的影响规律尚待从断裂力学和损伤力学计算方法及材料力学理论角度进一步去挖掘。此外,崩岗土体实际上并非完全均质、连续、各向同性,而由于软件的局限性,本次有限元模拟将其看做理想弹塑性体并认为土体符合摩尔—库仑本构,故后续有待根据崩壁土层的颗粒级配建立本构模型,采用PFC3D离散元软件从细观上定义颗粒之间的接触关系也许会更好地再现崩岗坡体崩塌的全过程,进而搜索出裂纹的产生位置。

