基于C-D的关联规则兴趣度挖掘算法*
阎 婷,吴文华,严丽娜,万 征
(1.国防科技大学信息通信学院试验训练基地,陕西 西安 710106;2.边海防学院教学考评中心,陕西 西安 710108)
0 引 言
传统的关联规则算法是针对关联关系计算它们的支持度和置信度来判断它们的关联程度,看它们之间是否具有很好的兴趣度。这些方法完全人为、主观地选择数据仓库,且力图用一种客观的、数学的方法评估主题,因此兴趣度的度量度并不高[1]。为了提高度量度,现提出一种新的计算关联规则兴趣度的方法,根据二维数据相对于坐标轴的位置度量兴趣度,称之为基于坐标的距离关联规则兴趣度挖掘方法,简称基于C-D的关联规则兴趣度挖掘算法。
1 算法描述
步骤1:利用Apriori算法和FP树等现有关联规则挖掘算法挖掘强关联规则。
步骤2:利用基于坐标的距离关联规则兴趣度挖掘方法判断哪些强关联规则是兴趣度较高的,将它们挖掘出来,剔除掉兴趣度较低的关联规则。这一步还需要分成几步进行。
(1)统计挖掘的强关联规则中左右两边各项在数据库中出现的次数;
(2)对每个关联规则都可以建立坐标轴,以箭头方向为正向,以箭头方向为反向,正向代表正项,反向代表负项(坐标的长短以事务出现次数衡量,哪一个是前提条件就作为横坐标X轴,另一个作为纵坐标Y轴)。
(3)用关联规则中左、右两边中次数较小者除以次数较大者,即对坐标进行单位化(为了使所有的关联规则在作兴趣度比较时都在同一个基础上)。
(4)考察坐标中的点到坐标中的对角线距离,离对角线距离越近,说明关联度越高。坐标在对角线上是一种理想的最大关联程度,所以以它为参考目标研究其他位置的点关联情况。兴趣度的范围在[0,/2]之间,离0越近,关联度越大。
2 算法说明
先对一个二维事务进行举例说明,再对多维数据库的关联规则进行举例分析,说明新的兴趣度关联规则是如何进行数据挖掘的。下面是一个二维事务的例子。
例:设有如表1所示的基本信息,根据定义可以得到关联规则。

表1 某交易集的基本构成信息
从表1可以得到的关联规则,如表2所示。

表2 某交易集的关联规则
根据现有关联规则挖掘算法挖掘8个强关联规则,描绘以上8个关联规则在坐标轴中的位置,下面给出买牛奶⇒买咖啡这一关联规则在坐标轴中位置,如图1所示。

图1 买牛奶、买咖啡坐标
以第一象限中的一个点为例,说明基于坐标的距离兴趣度关联规则是如何实现的。买牛奶买咖啡和买咖啡买牛奶的坐标点的位置都在第一象限,现以买牛奶⇒买咖啡进行说明。
先命名坐标数据以及所用到的线段和夹角。这里把买牛奶⇒买咖啡所在位置的点N到原点O这条线段起名为ON ,一三象限的对角线起名为Ob,ON 与Ob 的夹角起名为a,N点到对角线Ob的距离用d表示(即线段MN)。d越小,即离对角线越近,说明关联度越高,因为在对角线位置是一个极限位置。以第一象限为例说明:在第一象限对角线上的点是买牛奶的人全买了咖啡,其他象限同理。
从图1可以看出,要求N点到对角线Ob的距离,可以将问题归结到求出sina。前面已经给出两直线夹角余弦的公式,因为sina2+cosa2=1,所以只要求出sina,即可求出d。
对于点N到对角线Ob的距离给出计算过程,对角线的向量是s1={1,1},N点的向量s2={25,20},进行单位化20/25=0.8:1,可以计算坐标中点到对角线的距离范围为[0,2/2],所以兴趣度的范围在这个区间,且越接近0,兴趣度越高。现在对MN进行计算:

同理,可以求出买咖啡⇒买牛奶这一点到对角线的距离0.56(这里不给出算法过程)。由这两个数据可以知道,买牛奶⇒买咖啡的兴趣度高于买咖啡⇒买牛奶的兴趣度,因此买牛奶引起买咖啡的可能性很大程度上高于买咖啡引起买牛奶的可能性。由上面的叙述可以看出,没有将A⇒B和B⇒A同等对待,这是一个改进。与兴趣度相比不用两个阈值度量兴趣度大小,只用一个即可。对三维和四维甚至更高的维数,都可以采用上述方法计算,只是统计时关联规则的左边和右边可能是两项甚至是两项以上。只要对这一项出现的次数或者几项同时出现的次数进行统计,即可利用上述方法计算。
3 算法验证
上述算法说明中给出的例子有具体数值,但实际应用中是从事物数据库中找出具体的事务出现次数才能应用算法。下面给出一个例子进行说明。设事务数据库D如表3所示,D中包含9个事务,即|D|=9,最小支持数mincount=2,即最小支持度minsup=2/9=0.222。
利用经典的数据库关联规则挖掘算法:Apriori算法和FP树算法分别先挖掘出强关联规则[2],再利用本章提到的方法对这些关联规则进行判断。
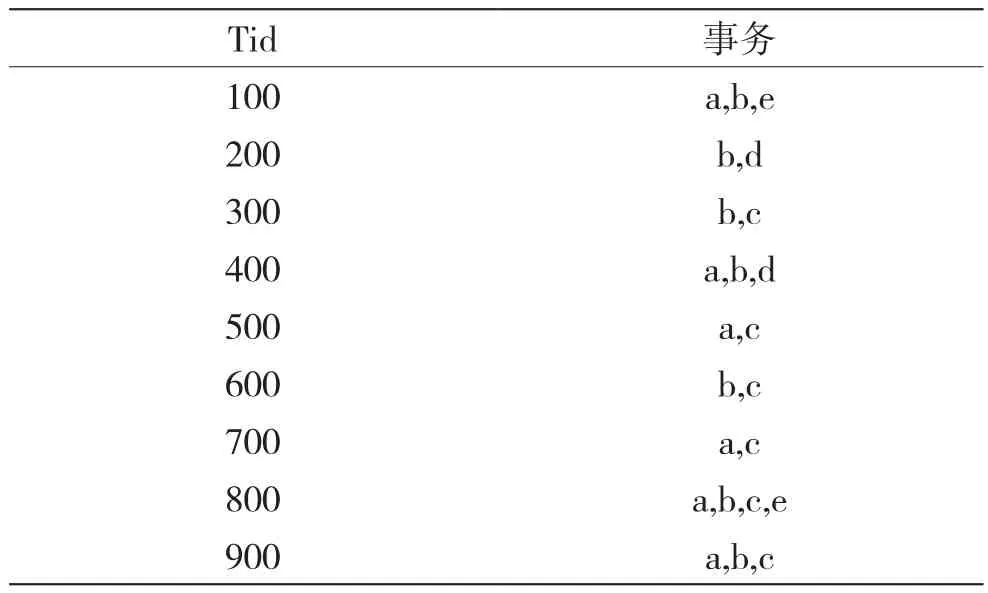
表3 事务数据库D
以上面的数据库为例给出算法的整个过程:
第一步,对于D中的每个事务所包含的频繁项目按照由大到小的的顺序进行排序,现把所有事务经处理后的结果列在表4中。

表4 排序后的事务数据库
第二步,利用FP树找关联规则,再利用本文算法判断规则的兴趣度高低。
先找到强关联规则,其中二维事务有{ab}、{ac}、{ae}、{bc}、{bd}、{be},三维事务有 {abc,abe}。可以从这棵树中找到每一个事务在其他事务中出现的次数,然后根据基于坐标的距离关联规则兴趣度挖掘方法算出兴趣度高的关联规则。
对使用Apriori算法和FP树后产生的频繁项目集l={a,b,e}[3],l的非空子集有{a,b}、{a,e}、{b,e}、{a}、{b}和{e},产生关联规则的置信度如表4所示。

表5 算法结果比较
第三步,利用基于C-D关联规则兴趣度挖掘方法找到兴趣度较高的关联规则。将它们和之前算法所得到的兴趣度作比较,如表5所示。
由表5可以看出,新兴趣度的算法度量出兴趣度的高低和置信度计算结果一致,范围在[0,,且越接近0,兴趣度越高。C-D兴趣度算法与支持度、置信度算法相比,优点在于它有一个范围限定,且它不需要两个阈值。与PS公式相比,优点在于它没有将A ⇒B和B ⇒A同等对待,所以是一个新的兴趣度度量算法。
4 结 语
文章给出了基于C-D关联规则兴趣度挖掘算法的步骤,并对算法进行了详细说明,用实例对算法过程做出了详细描述,将Apriori算法和FP树的算法与基于C-D兴趣度算法进行比较,充分证明了新兴趣度算法的实用性。

