基于Elman模型的动态障碍物运动状态估计*
赵久国,石 韬
(1.渤海造船厂集团有限公司,辽宁 葫芦岛 125004;2武汉哈船导航技术有限公司,湖北 武汉 430070)
0 引 言
学习是人类具备的重要能力,目前计算机已经拥有进一步学习的能力。机器学习借助主动学习过去众多数据信息中所蕴含规律的手段,可以得到新信息与新经验,进一步增强计算机的智能性,最终让与人类相近的决策能力在计算机上体现[1]。随着大数据和硬件技术的计算和存储能力的发展,机器学习的研究也在飞速发展。机器学习属于新兴领域,当前依旧处于基础研究过程,因此同人的大脑相比,计算机在解决问题方面依然存在一定的不足[2]。借助大量数据自动获取对应结论是机器学习最重要的目标,这主要是一个借助数学与统计学手段获得待解决问题的最优答案的过程[3]。
本文的预测模型以Elman在1990年提出的Elman神经网络为基础,结合预测控制模型,以障碍物当前的位置推断得到其运动改变数据,并且经过长时域的改进,最终得到障碍物与实际情况最相似的运动状态数据。
1 Elman预测控制结构的设计
模型预测控制是一种新型计算机控制算法,模型预测控制算法因为借助了多步预测、滚动优化和反馈校正等控制思想,所以具有较好的控制效果、较强的鲁棒性、对模型精确性没有较高要求等优势[4]。
对于预测控制来说,最重要的部分是构造出一个契合真实情况的模型进行预测。这部分需要借助历史数据作为样本,然后才可以使用构造的模型预测未来数据[5]。使用预测控制模型并进行长时域优化,可实现根据历史数据预测得出与障碍物实际运动最相似的运动数据。本节使用预测控制模型与Elman神经网络相结合的方法,具有预测模型、滚动优化和反馈校正3个特点[6]。Elman网络预测模型的预测控制组成如图1所示。

图1 神经网络预测控制结构
设输入历史样本数据为r,通过参考轨迹环节后获得预测数据yr,预测数据和期望数据之间的误差为:
ec=yr-yk(1)
通过滚动优化环节得到控制信号u,将其使用在受控目标上获取系统输出y,ym表示Elman网络预测模型输出,yp表示经由改正后的输出。借助Elman网络推断出将来k(k≥1)步的输出,随后把这个推断数据应用在反馈校正装置后传递给滚动优化控制器改进,得到接下来步骤的控制量,以实现更有效的实时搜寻障碍物数据信息。Elman预测模型的输出与系统输出之间的误差为em=y-ym,此误差用于训练神经网络的的连接权值,且按照ec和反馈的梯度信息∂ym/∂u滚动改进非线性系统,进而优化计算后续步骤的控制量。
算法实现的主要过程:第一步使用Elman神经网络识别非线性系统,解决人工神经网络不能对受控目标进行多步建模并实时预测的难点;第二步构造Elman网络模型进行预测,实现滚动优化控制非线性系统。
2 建立Elman预测模型
使用Elman预测并通过加入内部反馈信号表现非线性运动学问题,可以解决由于障碍物的非线性运动产生的传统人工神经网络不能解决的动态信息处理问题。由Elman神经网络构建的单层网络可很好地描述复杂的动态系统。
构建预测模型过程中,将滞后的正确系统的输入输出数据作为样本应用到预测网络模型,可得到未来k时刻的输出数据。所构建的Elman网络模型为:
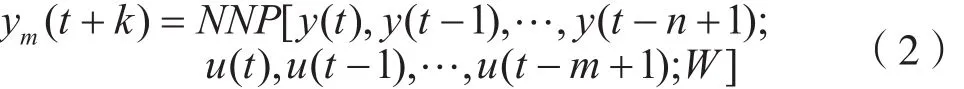
式中,预测模型的输出值为ym,预测步长为k,系统t时刻的输出为yt,系统t时刻的输入为u(t),系统输入和输出的滞后时间由m和n表示且n≥m,Elman的网络权值为W。
模型的输入为:

模型的输出为:

式中Hjm(t)为隐层低j个神经元在t时刻的输出,具体形式如下:

f代表隐层的激活函数,其表达式为:

Elman预测网络的误差模型为:
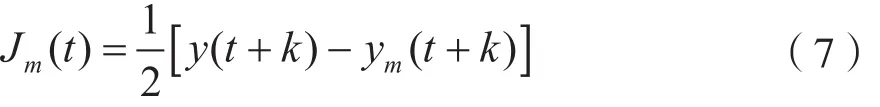
令a=y(t+p)-ym(t+p),网络权值的调节量为:
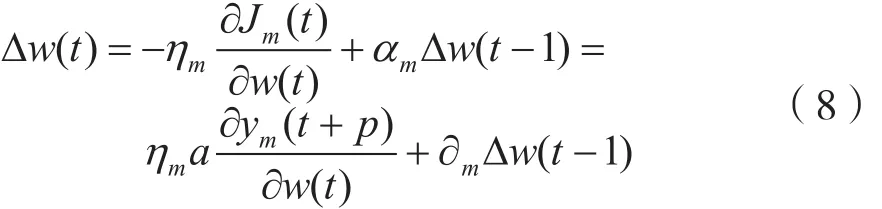
式中:ηm表示学习率,αm表示动量因子。于是,可以得到网络权值大小的调整由网络计算误差决定,调节程度跟随网络误差同时增加或减少。为了解决系统y(t+k)时刻的输出数据不能在t时刻得出的问题,使用时间差分法(简称TD法)实现用相邻预测输出间的误差代替预测与实际输出间的误差。作为强化学习方法中的一种,它为克服此难点提供解决途径。
TD算法的原理是指临近两次的网络输出不针对相同时刻输出的预测,参考式(1)和式(2)能够得到在t时刻网络的输入表示为xm(t),相应的输出是ym(t+k),用Ykt表示;在t+1时刻的输入表示为xm(t+1),对应的输出为ym(t+1+k),用Ykt+1表示。说明两个输出之间不存在必然的期望关系,得到的规律为:
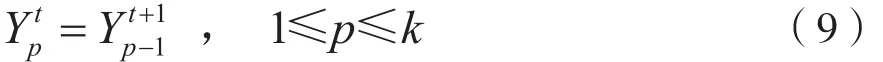
当前网络的误差性能指标表示为:
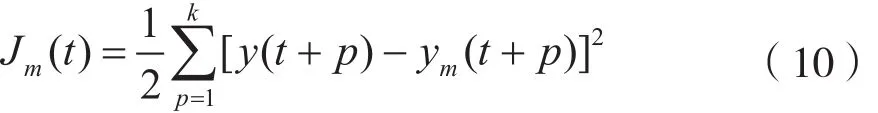
把系统实际输出y(t+p)与网络预测输出ym(t+p)之间的偏差描述成当前时刻t之后的预测变化之和[7]是TD法求解问题的重点,表示为:

式(11)中系统t时刻的真实输出由Yt0表示。通过上述说明在把式(7)代入式(10),令:

获得的Elman网络的学习方法为:
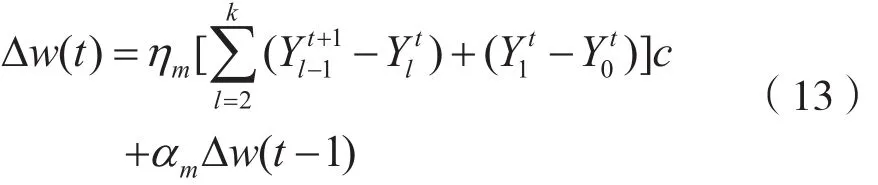
3 反馈校正模型及参考轨迹的建立
在预测控制模型中,动态预测问题可分为模型输出的预测数据和根据偏差所产生的校正数据两部分。在真实条件下,不能排除时变性、非线性以及随机干扰等问题所带来的影响,因此输出数据与系统实际输出相比具有较大偏差。想要使系统更加精准,可以借助反馈校正环节实现[8]。
期望输出与模型预测输出之间的误差,由预测控制模型实时计算得出,模型的学习能力使用误差信号进行改进,逐渐提高预测能力。因为t时刻的预测误差会影响t+1,t+2,…,t+p-1时刻的预测误差,所以应用反馈校正借助误差修正因子,线性改进预测模型未来的输出预测值。反馈校正可在线进行也可离线进行,模型预测值为[9]:

式中,误差修正加权因子为h。因为该系数补偿了偶然因素的误差,所以大多数情况下选择经验试凑法选择h,并不能精确地表达数学模型。
参考轨迹可使输出信号按照规定轨迹到达设定大小,使系统不产生过量控制。参考轨迹yc的数学模型为:
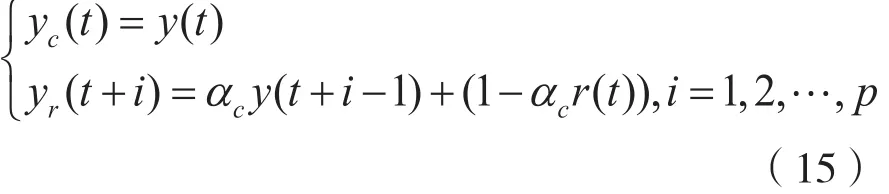
式中,平滑因子为αc∈[0,1),设定值由r(t)表示。由式(15)可知,系统的鲁棒性和平滑性将随着平滑因子的增大而变好,但系统的处理速度会变的相对缓慢。所以,选出合适的平滑因子,对平衡系统性能尤为重要。
4 滚动优化算法设计
为实现最优控制,选择优化算法,针对每一步数据的将来有限步进行优化计算,其模型为时间t的滚动优化模型。t时刻的预测指标模型为:
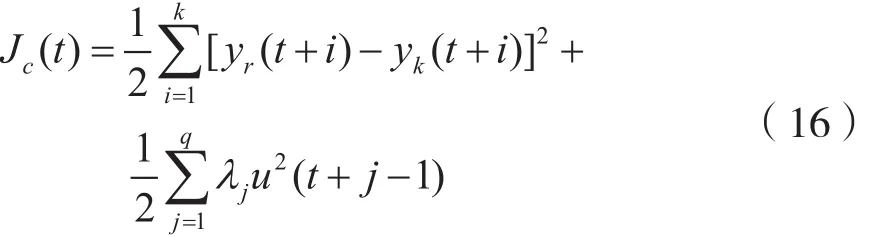
式中,q为控制时域,k为预测时域,λj>0是加权系数,通常情况下k≥q≥1。
当Jc值最小即令∂Jc(t)对u的偏导数等于0时,目前数据以及将来要采取控制的序列便可满足约束条件,同时还可以求出未来q个控制变量u(t),u(t+1),…,u(t+q-1)。

根据式(17),最优控制量可以用yk(t+k)来计算,即未来k步的预测输出yk中的第k步预测值。这种方法的好处为改变控制量的时刻为t时刻,其他步并不需要改变,控制量将会在t+1时刻被重新计算。
式(17)中,令 ∂Jc(t)/∂u=0,可得:

由 式(14), 可 用 ∂ym(t+k)/∂u(t)近 似 取 代∂yk(t+k)/∂u(t)。
5 实验结果
使用Matlab对Elman预测模型方法的动态障碍物运动状态预测的有效性进行仿真验证。假设障碍物运动轨迹为随机路线,图2是使用Elman模型预测的障碍物运动轨迹图,图3是预测轨迹局部放大图,图4和图5是经度和纬度预测误差图。
由图2任意路线的轨迹预测可知,基于Elman预测模型算法能够较好地预测动态障碍物的运动轨迹。由图3可以看出,预测轨迹对于任意轨迹的拟合都有较好的效果。由图4经度方向预测误差和图5纬度方向预测误差得出结论,预测轨迹经度方向、纬度方向最大误差分别为0.75 m、0.62 m。

图2 任意路线轨迹和预测路线

图3 任意路线轨迹预测局部放大
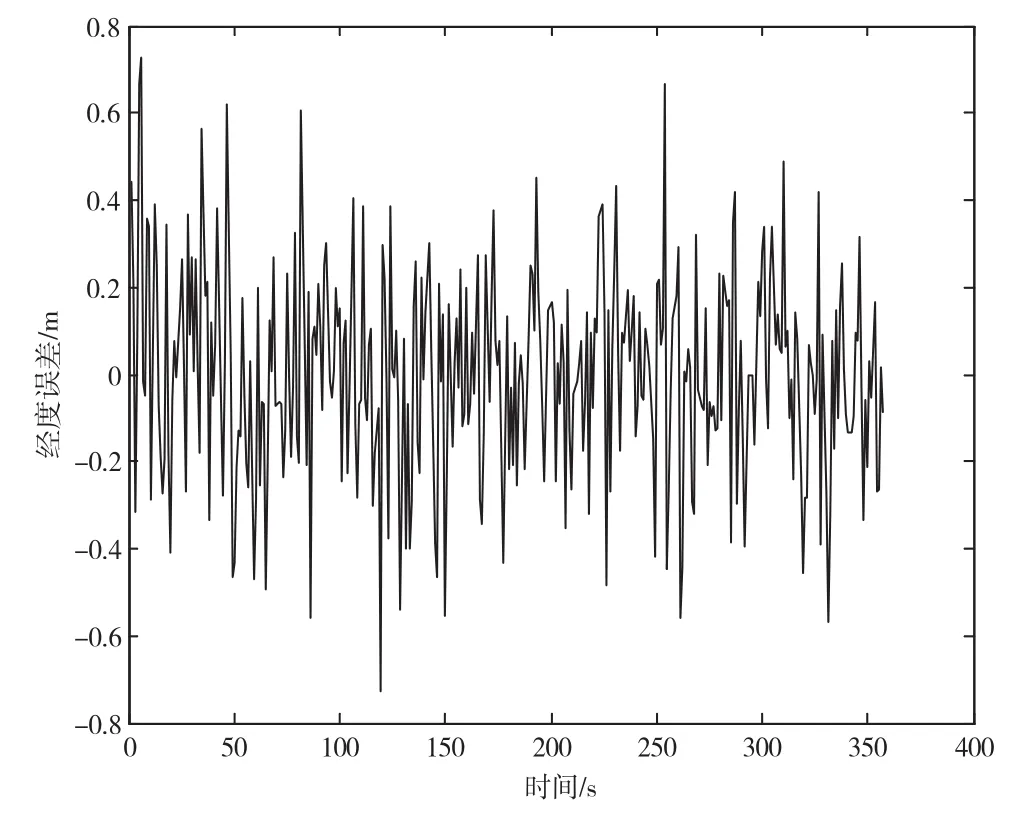
图4 经度方向预测误差

图5 纬度方向预测误差
综上可以得出结论:Elman神经网络能够将经度、纬度方向的预测误差控制在0.8 m以内,当障碍物运动轨迹为转弯时,可以较为平滑地处理运动轨迹,没有出现大角度转向情况,与实际情况较为吻合。作为预测控制的预测模型,Elman神经网络能够较好地预估动态障碍物的运动轨迹,为无人艇的避碰行为提供有效的帮助。
6 结 语
本文针对动态障碍物利用基于Elman神经网络作为预测模型组成预测控制系统的方法对其进行运动状态预测,使无人艇能够准确判断障碍物的方位及运动轨迹的信息。首先设计控制系统预测模型结构,确定输入输出以及各参数之间的关系;其次设计算法模型,对各参数之间建立定量分析;最后通过任意路线曲线实例进行仿真,得出经纬度误差都在0.8 m以内的结论,验证预测模型的可行性。本文对未来无人艇动态障碍物的轨迹预测研究打下了坚实基础。

