基于Copula的京津冀平原作物水分利用效率驱动因子分析*

龙学智, 刘苏峡**, 莫兴国, 陈学娟

基于Copula的京津冀平原作物水分利用效率驱动因子分析*

龙学智1,2, 刘苏峡1,2**, 莫兴国1,2, 陈学娟1,2

(1. 中国科学院地理科学与资源研究所陆地水循环及地表过程重点实验室 北京 100101; 2. 中国科学院大学资源与环境学院/中丹学院 北京 100049)

农业是京津冀地区最主要的用水部门, 提高农业用水效率有助于缓解京津冀水资源压力, 实现可持续发展。基于VIP模型模拟的1980—2013年京津冀平原作物水分利用效率(WUE)、作物净初级生产力(NPP)、作物实际蒸散发(ETa), 结合同期年平均气温(Tmean)、年降水量(Pre)和年日照时数(Sun), 应用Copula函数理论分别建立WUE与NPP、ETa、Tmean、Pre、Sun的5组联合概率分布函数, 计算各驱动因子在低、中、高取值条件下WUE大于任一特定取值的可能性(定义为WUE条件概率), 探索WUE的驱动关系。结果表明: 1)驱动因子NPP、ETa、Sun取值越大, WUE大于任一特定取值的可能性越大; 而驱动因子Tmean和Pre取值越小, WUE大于任一特定取值的可能性越大。2)若以各驱动因子分别在高、低取值条件下的WUE条件概率的差值来反映WUE对各驱动因子大小的敏感程度, WUE对NPP的大小最为敏感, 而后依次是Sun、ETa、Pre、Tmean。3)对比不同驱动因子相同取值条件下的WUE条件概率, 较低的NPP会明显抑制WUE的大小, 提高NPP对WUE的提升有明显的保障作用。综上所述, 作物WUE同时受光合作用和蒸腾作用两个生理过程控制, 较难确定光合和蒸腾对WUE的驱动关系; WUE与驱动因子的联合概率分布和条件概率分析指出, 在京津冀平原可以采用在控制耗水的条件下提高NPP的策略, 该策略可能比在控制产量的条件下减少耗水的策略更有效。

京津冀平原; 作物水分利用效率; 驱动因子; Copula函数; VIP模型; 作物净初级生产力(NPP)

京津冀以北京为核心, 天津和河北为两翼, 是我国政治、经济、文化和科技中心。《京津冀协同发展规划纲要》将其定位为“以首都为核心的世界级城市群、区域整体协同发展改革引领区、全国创新驱动经济增长新引擎、生态修复环境改善示范区”。1956—2014年京津冀地区多年平均水资源量约为240亿m3, 水资源公报统计的2001—2016年平均水资源量约为183亿m3, 较多年平均值减少约24%, 且人均水资源量不到全国平均水平的1/10, 水资源极其紧缺[1-2]。京津冀地区长期过度开发利用水资源来支撑经济社会的发展, 引起了一系列的水环境问题, 如河道断流、水体污染严重、地下水漏斗等, 水资源已经成为限制地区发展的关键要素[1]。

水资源公报数据显示, 2001—2016年京津冀地区多年平均农业用水量约为171亿m3, 约占地区总用水量的67%左右, 是京津冀地区最主要的用水部门, 也被广泛认为是地下水过度开采的主要原因[3]。京津冀地区广泛采用冬小麦()和夏玉米()一年两熟轮作的耕种模式, 其中冬小麦生育期降水量远低于作物需水量, 地下水灌溉成了农业生产的重要保障[4]。因此, 提高农业用水效率是缓解京津冀地区水资源压力的有效途径, 也是实现可持续发展的关键。

农业种植的用水过程可以概括为3个主要环节, 即从水源输水到农田的过程、田间灌溉过程、作物吸收及生长过程, 因此便产生了对应上述3个过程的农业用水效率评价方法, 分别为输配水效率、田间灌水效率、作物水分利用效率[5-6]。灌溉水有效利用系数常被用作灌溉用水效率的表征指标, 通常表示为灌入田间可被作物利用的水量与灌溉用水总量之比, 也可以表示为输配水效率与田间灌水效率的乘积, 是一个无量纲数。作物水分利用效率则反映的是作物吸收水分并进行光合作用生成产物的过程对应的用水效率, 表示为作物产量与蒸散发量的比值。冯保清[6]详细梳理了不同尺度灌溉用水效率评价的理论和方法, 确定了灌区、省级区域、全国这 3个尺度的灌溉水有效利用系数的评价方法, 并研究了相应的影响因素。随着遥感技术的发展, 基于遥感信息的作物水分利用效率得到了广泛的研究, 尚松浩等[5]总结了遥感技术在蒸散发模型和作物估产模型等方面应用的研究进展, 并评述了其在作物水分利用效率评价中的应用情况。目前, 遥感信息与模型结合的作物水分利用效率研究已经在多个区域和不同尺度得到广泛开展[7-10]。此外, 以经济学为基础的全要素农业用水效率的理论和应用也在近年得到迅速发展,在多个区域和不同尺度范围均有应用[11-12]。

采用多种统计方法分析水文时间序列已有长足进展[13]。Copula函数理论被引入水文水资源研究后, 其在多变量水文分析中得到了广泛的应用[14]。熊立华等[15]较早地在国内水文研究中介绍了Copula函数的定义、属性和构造方法, 并尝试建立了河流上下游两个站点的最大洪水联合分布函数。Salvadori等[16]系统性介绍了Copula函数在水文极值及其重现期研究中的应用。Hao等[17]应用Copula函数及条件概率分析对中国东部地区由极端高温引起的干旱进行了风险评估; Madadgar等[18]应用Copula函数和条件概率分析研究了降水量和土壤湿度与农作物产量的关系, 用于估计干旱对作物产量的影响。

目前, Copula函数理论在农业用水效率研究中的应用较少, 特别是在作物水分利用效率的研究中尚少见报道。李浩鑫等[19]基于传统的灌溉用水效率评价指标体系, 建立了PCA-Copula灌溉用水评价方法, 并在7个灌区进行了实证分析。Zhao等[20]应用Copula函数建立了灌溉用水量与灌溉用水效率的联合分布, 并分析了不同水平年的河流流量与灌溉用水效率的关系。

本文以京津冀平原为研究区, 应用Copula函数理论分别建立作物水分利用效率(water use efficiency, WUE)与作物净初级生产力(net primary productivity, NPP)、作物实际蒸散发(actual evapotranspiration, ETa)、年平均气温(annual mean temperature, Tmean)、年降水量(annual precipitation, Pre)、年日照时数(sunshine duration, Sun)等5个随机变量的5组联合分布, 采用条件概率分析研究WUE与NPP、ETa、Tmean、Pre、Sun 5个驱动因子的关系, 建立WUE相对于上述各因子的Copula谱系, 探索提高WUE的潜在途径以缓解地区水资源压力。

1 研究区概况及数据资料

1.1 研究区概况

京津冀平原是北京市、天津市和河北省的全部平原区, 是华北平原的一部分, 西起太行山脉, 北靠燕山山脉, 东临渤海, 总面积约9.5´104km2。京津冀平原为温带大陆性季风气候, 降水在年内分布不均, 主要集中在6—9月。京津冀平原绝大部分属于海河流域, 为我国严重缺水地区, 地下水超采严重。研究区内主要采用冬小麦和夏玉米一年两熟轮作的耕种模式, 小麦和玉米的播种面积占粮食作物总播种面积的80%左右, 灌溉用水主要依赖地下水。

1.2 数据资料

本文采用的WUE被定义为NPP和ETa的比值, NPP和ETa数据来源于VIP分布式生态水文模型(vegetation interface process model, 简称VIP模型)对研究区1980—2013年的模拟结果[21]。VIP模型以降水、气温、日照时数、相对湿度和大气压等气象要素作为驱动, 基于DEM数据、土壤类型、土地利用类型和植被类型等地理信息, 模型具体设置和模拟验证参见文献[21]。

分析所用的平均气温(Tmean)、降水(Pre)和日照时数(Sun)等气象数据来自中国气象科学数据共享服务网, 采用ANUSPLIN插值软件, 基于研究区的DEM数据, 经空间插值获得。

利用研究区土地利用类型资料提取出1980—2013年京津冀平原耕地, 再根据VIP的输出结果和气象要素输入数据, 获得WUE、NPP、ETa、Tmean、Sun和Pre 6个变量在1980—2013年空间平均值的时间序列数据。

2 研究方法

2.1 单变量概率分布函数估计

随机变量概率分布函数估计是水文频率分析的核心内容, 主要包括分布函数的选择和参数的估计两个关键问题, 从而实现对水文变量总体概率分布的描述。分布函数的选择即线型的选择, 目前国内外常用的线型有十几种, 本文以正态分布、Gamma分布、GEV分布、极值分布(extreme value distribution, EV)和Logistic分布作为备选分布函数。分布函数的参数估计方法主要有矩法、权函数法、适线法和最大似然估计法等方法, 本文采用最大似然估计法进行随机变量分布函数的参数估计。

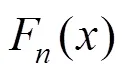
采用Gringorten公式来计算经验频率, 其表达式为:

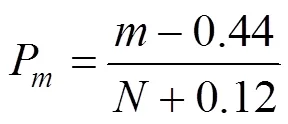
应用最大似然估计法分别对备选分布函数进行参数估计, 由K-S检验样本是否服从相应理论分布, 再通过比较均方根误差RMSE优选最合适的分布函数。

2.2 二维Copula联合分布函数

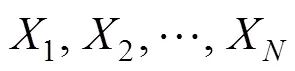
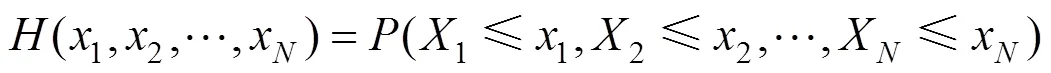
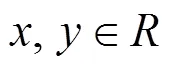
如果和连续, 则是唯一的。如果是一个Copula函数, 且和分别为边缘分布, 则是和的一个联合分布函数。

2.2.1 Copula函数形式

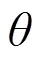
表1 Copula函数形式及参数取值范围

和分别为随机变量和边缘分布函数, 分别表示随机变量≤的概率和随机变量≤的概率。为Copula函数的参数。andis the probability distribution function of random variableand, respectively, which is the probability whenis not large than observedandis not large than observedrespectively.is the parameter of Copula function.

2.2.2 Copula函数的参数估计

目前常用的Copula函数参数估计方法主要有Kendall相关系数法、最大似然估计法、适线法等。Sadegh等[22]提出了基于马尔科夫链蒙特卡罗模拟(Markov chain Monte Carlo, MCMC)的Copula函数参数估计算法, 并开发了多变量Copula分析工具箱(Multivariate Copula Analysis Toolbox, MvCAT)。本文应用MvCAT工具进行Copula函数的参数估计。

2.2.3 Copula函数的拟合检验

Zhang等[23]引入AIC指标(Akaik’s information criterion, AIC)用于Copula函数的优选, 其表达式为:

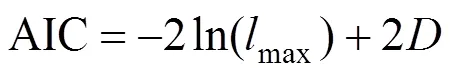
此外, RMSE也被用于反映Copula函数的拟合情况, 表达式如下:

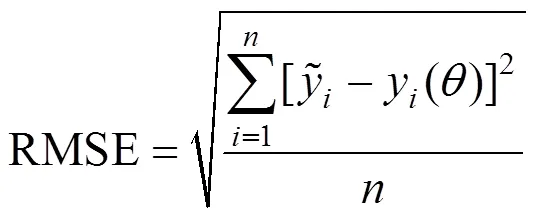
2.3 基于二维Copula函数的条件概率

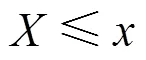
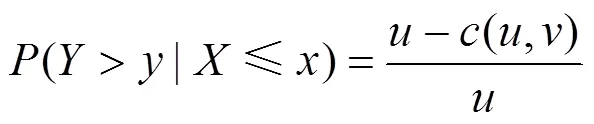
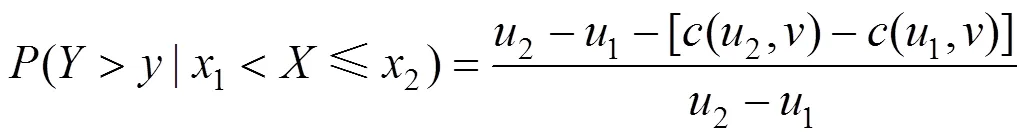
3 结果与分析

3.1 WUE及相关变量的边缘分布拟合

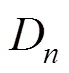
S检验, 表明5种备选分布函数均能用于拟合WUE等6个随机变量的分布。以RMSE作为评价边缘分布拟合情况的依据, RMSE越小则拟合结果越好, 不难发现WUE、NPP和ETa 3个VIP模型模拟的变量分别用EV分布、正态分布和Logistic分布能够较好地拟合其边缘分布, 而Tmean、Sun和Pre 3个气象要素则均能通过GEV分布实现较好的边缘分布拟合。最大似然估计法给出了6个变量所对应的边缘分布函数的参数估计值, 相应的边缘分布函数及参数如表3所示。

表2 1980—2013年研究区作物水分利用效率及相关变量的边缘分布假设检验结果

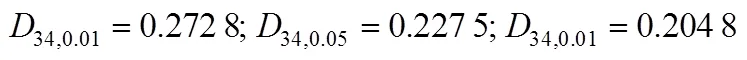
表3 1980—2013年研究区作物水分利用效率及相关变量的边缘分布函数

WUE、NPP、ETa、Tmean、Sun、Pre 6个随机变量的边缘分布函数, 拟合情况如图1所示。柱状图为各随机变量观测样本的概率密度, 表示为区间内样本量与样本总量的比值再除以区间长度, 柱状图面积的总和等于1; 点划线是根据RMSE最小准则所选定的边缘分布函数计算的概率密度函数, 不难发现, 概率密度函数能够较好地反映各随机变量的概率分布情况。图1中虚线表示各随机变量的经验频率, 实线则表示边缘分布函数拟合的理论累计概率, 结果表明根据RMSE最小准则所选定的边缘分布函数拟合情况较好, 参数估计合理, 因此, WUE、NPP和ETa分布服从EV分布、正态分布和Logistic分布, Tmean、Sun和Pre服从GEV分布。

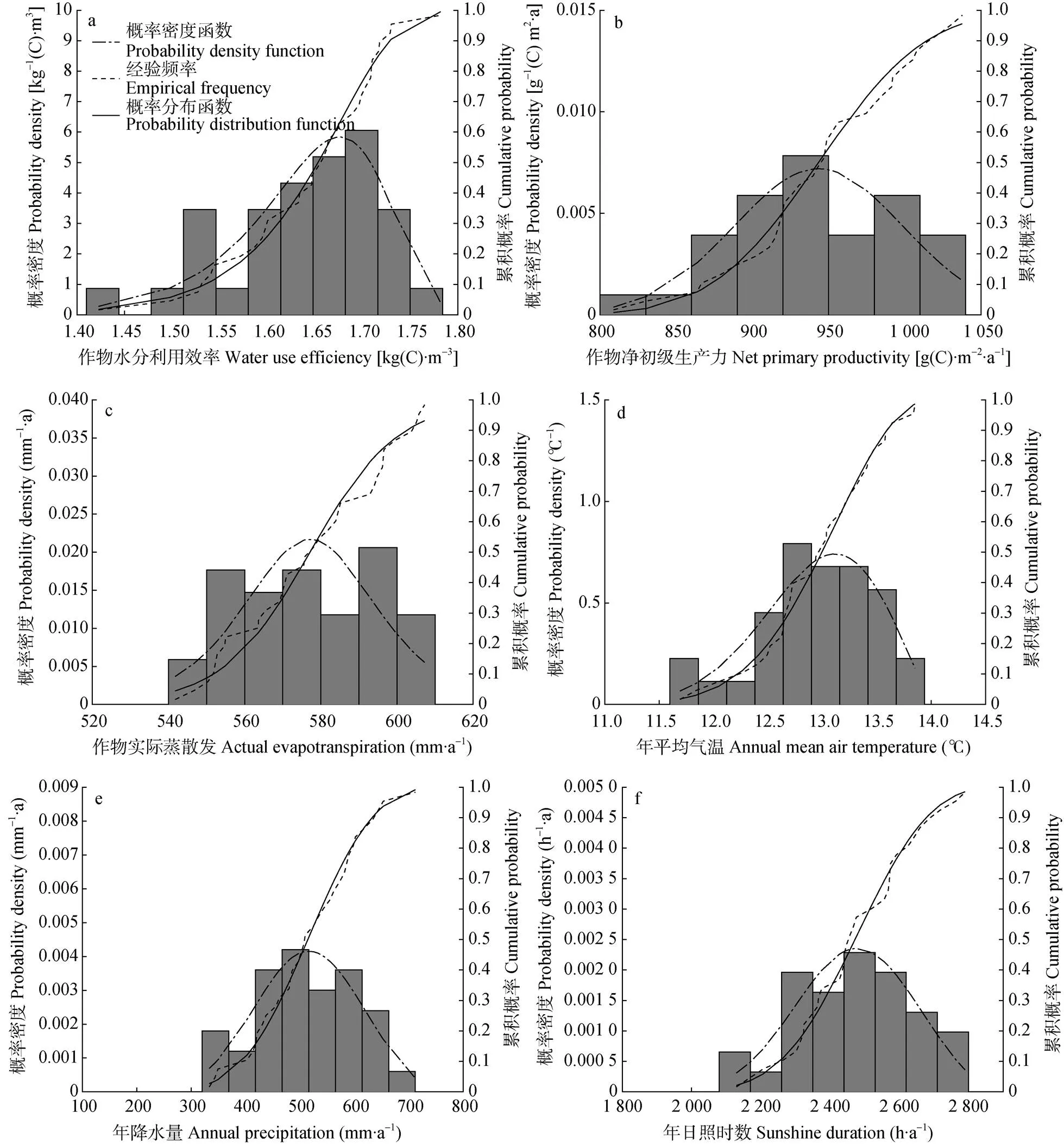
图1 1980—2013年研究区作物水分利用效率(a)、作物净初级生产力(b)、作物实际蒸散发(c)、年平均气温(d)、年降水量(e)和年日照时数(f)概率分布拟合情况

3.2 WUE与相关变量的Copula联合分布拟合及检验

Copula函数能够连接两个随机变量的边缘分布函数, 从而构建两变量联合分布函数。选用Gaussian、Frank、AMH、FGM、Cubic 5种形式的Copula函数, 构建WUE-NPP、WUE-ETa、WUE-Tmean、WUE-Pre、WUE-Sun 5组两变量联合分布函数。采用MvCAT工具箱的MCMC方法估计Copula函数待定参数, 并进行K-S检验, 结果如表4所示。对于WUE-NPP等5组联合分布而言, 在0.01的显著性水平下, Gaussian、Frank、AMH、FGM、Cubic形式的Copula函数拟合结果的D值均小于34,0.01, 通过K-S检验, 表明上述5种形式的Copula函数均可用于拟合WUE-NPP、WUE-ETa、WUE-Tmean、WUE-Pre、WUE-Sun联合分布, 需要进一步比较拟合结果的RMSE和AIC选择最合适的Copula函数。

表5为5种Copula函数分别拟合WUE-NPP、WUE-ETa、WUE-Tmean、WUE-Pre、WUE-Sun 5组联合分布的RMSE和AIC, RMSE和AIC越小则拟合结果越好。Gaussian形式的Copula函数对WUE-NPP和WUE-ETa两组联合分布的拟合结果最优; AMH形式的Copula函数对WUE-Pre和WUE-Sun两组联合分布的拟合结果最优; 对于WUE-Tmean联合分布, Cubic形式的Copula函数拟合结果的RMSE和AIC最小, 但表4所给出的该Cubic函数的参数估计值为-1, 在取值范围的边界处收敛, 可能会引起不确定性, 因此, 选择次优的FGM形式的Copula函数更合适。

图2为Gaussian形式Copula函数对WUE-NPP和WUE-ETa联合分布的拟合情况, FGM形式Copula函数对WUE-Tmean联合分布的拟合情况, 以及AMH形式Copula函数对WUE-Pre和WUE-Sun联合分布的拟合情况。横轴为Copula联合分布函数计算的理论概率, 纵轴为经验频率, 图2中由经验频率与理论概率构成的点分布在45°斜线附近, 且2均在0.97以上, 表明选取的Copula函数对各联合分布的拟合情况较好, 能够反映WUE-NPP等5组联合概率分布情况。

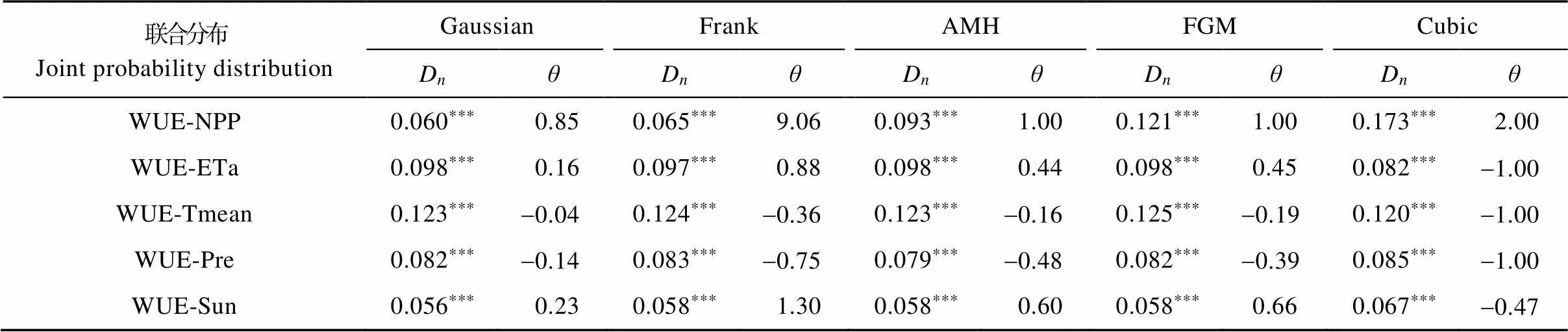
表4 1980—2013年研究区作物水分利用效率与各相关变量联合分布的Copula函数K-S检验及参数估计值

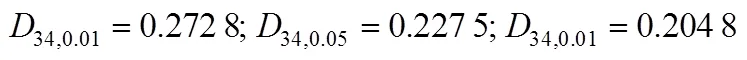
表5 1980—2013年研究区作物水分利用效率与各相关变量联合分布的Copula函数RMSE和AIC值

WUE-NPP: 作物水分利用效率和作物净初级生产力的联合分布; WUE-ETa: 作物水分利用效率和作物实际蒸散发的联合分布; WUE-Tmean: 作物水分利用效率和年平均气温的联合分布; WUE-Pre: 作物水分利用效率和年降水量的联合分布; WUE-Sun: 作物水分利用效率和年日照时数的联合分布。针对每组联合分布, 5个备选Copula函数的拟合结果中最小的RMSE和AIC加粗, 表明拟合结果最优, 相应的Copula函数用于描述作物水分利用效率和各相关变量的联合分布情况。WUE-NPP: the joint probability distribution of water use efficiency and net primary productivity. WUE-ETa: the joint probability distribution of water use efficiency and actual evapotranspiration. WUE-Tmean: the joint probability distribution of water use efficiency and annual mean air temperature. WUE-Pre: the joint probability distribution of water use efficiency and annual precipitation. WUE-Sun: the joint probability distribution of water use efficiency and sunshine duration. The smallest RMSE and AIC among 5 candidate Copula functions was bolded, standing for the best fitting of the joint probability distribution of water use efficiency and other relevant variables.

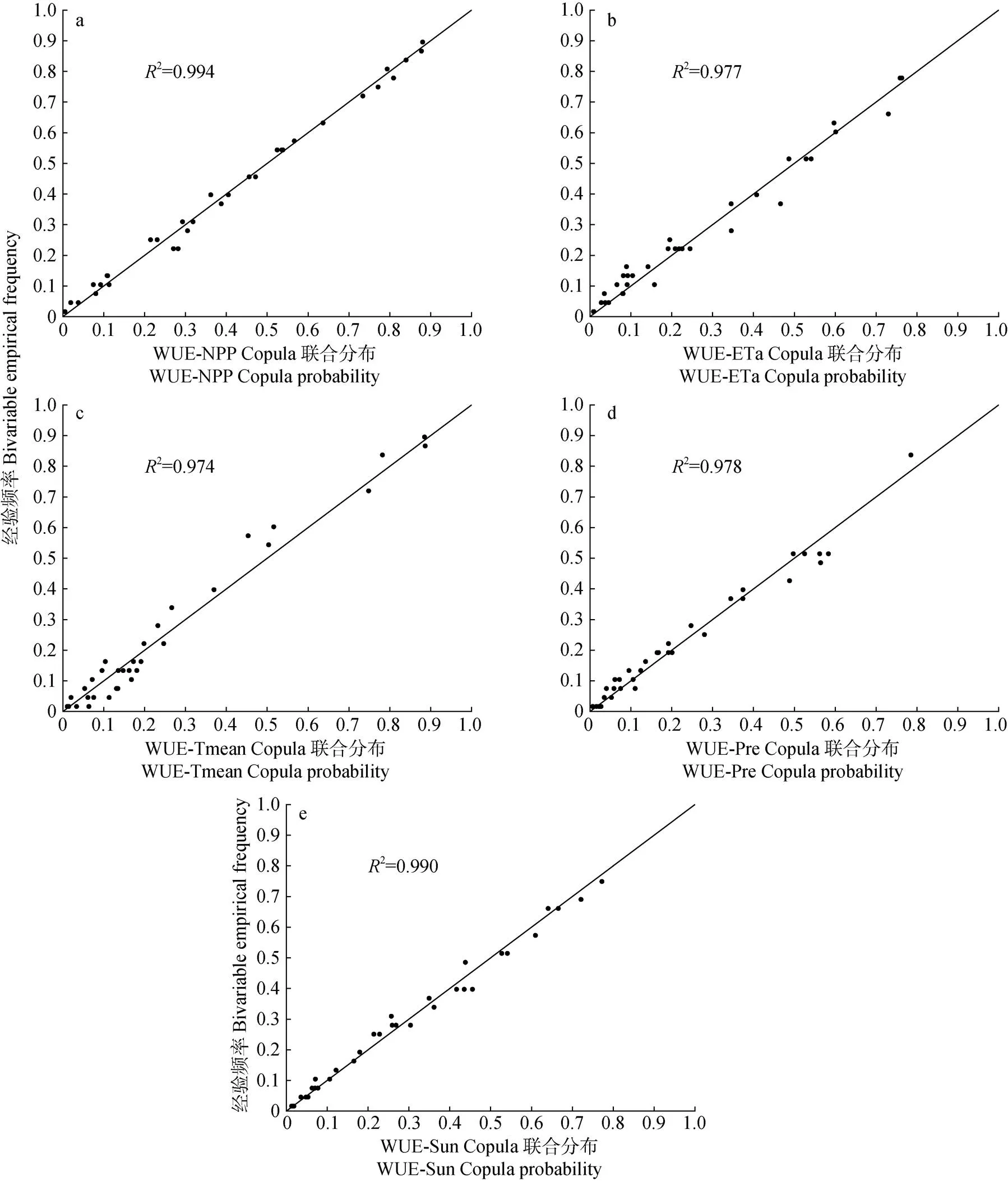
图2 1980—2013年研究区作物水分利用效率分别与作物净初级生产力(a)、作物实际蒸散发(b)、年平均气温(c)、年降水量(d)、年日照时数(e)的联合分布的拟合情况

WUE-NPP: 作物水分利用效率和作物净初级生产力的联合分布; WUE-ETa: 作物水分利用效率和作物实际蒸散发的联合分布; WUE-Tmean: 作物水分利用效率和年平均气温的联合分布; WUE-Pre: 作物水分利用效率和年降水量的联合分布; WUE-Sun: 作物水分利用效率和年日照时数的联合分布。WUE-NPP: the joint probability distribution of water use efficiency and net primary productivity. WUE-ETa: the joint probability distribution of water use efficiency and actual evapotranspiration. WUE-Tmean: the joint probability distribution of water use efficiency and annual mean air temperature. WUE-Pre: the joint probability distribution of water use efficiency and annual precipitation. WUE-Sun: the joint probability distribution of water use efficiency and sunshine duration.

3.3 WUE条件概率分析

聚焦WUE受NPP、ETa、Tmean、Pre、Sun等变量大小的影响, 根据各变量边缘分布函数上33%和67%两个分位点, 将NPP、ETa、Tmean、Pre、Sun划分为低(Low, L)、中(Medium, M)、高(High, H)3种取值情形, 使各变量为低(L)、中(M)、高(H)取值的可能性均为33%左右, 如表6所示, 并在此基础上建立WUE条件概率分布。

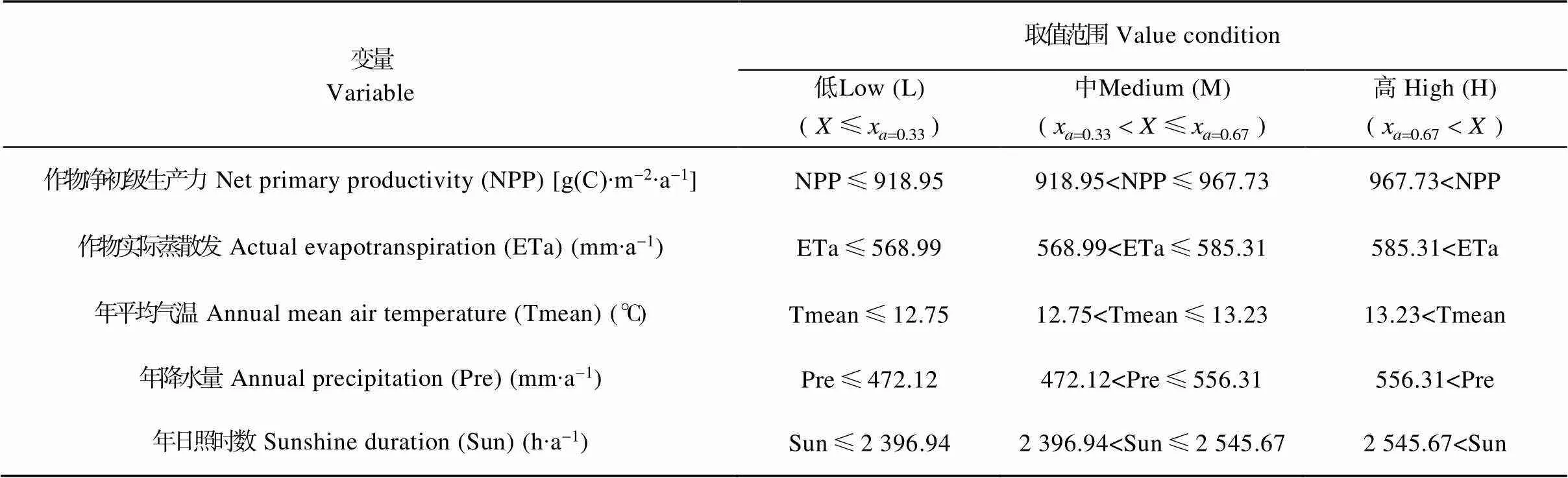
表6 研究区作物水分利用效率的相关变量的取值条件

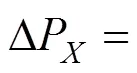
图3 作物净初级生产力(NPP, a)、作物实际蒸散发(Eta, b)、年平均气温(Tmean, c)、年降水量(Pre, d)、年日照时数(Sun, e)在低(L)、中(M)、高(H)取值条件下的作物水分利用效率的条件概率分布

P|L,P|M, andP|Hare the conditional probability distribution of water use efficiency under low (L), medium (M), and high (H) value conditions of net primary productivity, actual evapotranspiration, annual mean air temperature, annual precipitation, and sunshine duration.

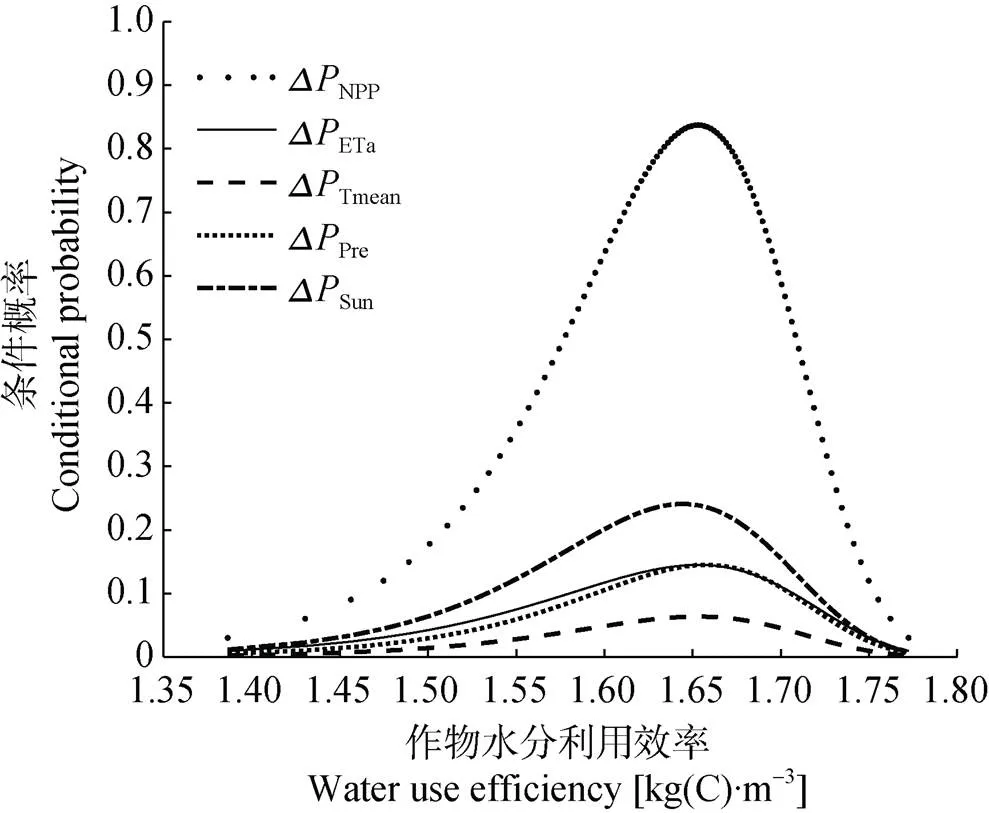
图4 研究区作物水分利用效率对相关变量大小的敏感程度

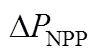
4 结论与讨论

本文以水资源紧缺的京津冀平原为研究区, 应用Copula函数理论分别建立WUE与NPP、ETa、Tmean、Pre、Sun 5个相关变量的5组联合分布函数, 采用条件概率分析研究了WUE与5个潜在驱动因子之间的关系, 得到以下结论:

1)WUE条件概率指驱动因子在不同取值条件下WUE大于任一特定取值的可能性。驱动因子NPP、ETa、Sun取值越大, WUE大于任一特定取值的可能性越大; 而驱动因子Tmean和Pre取值越小, WUE大于任一特定取值的可能性越大。

2)若以各驱动因子分别在高、低取值条件下的WUE条件概率的差值来反映WUE对各驱动因子的敏感程度, 结果显示, 京津冀平原耕地WUE对NPP的大小最为敏感, 而后依次是Sun、ETa、Pre、Tmean。

3)作物WUE同时受光合作用和蒸腾作用两个生理过程控制, 较难确定光合和蒸腾对WUE的驱动关系, 本文从WUE与驱动因子的联合分布和条件概率分析指出, 在京津冀平原采用在控制耗水的条件下提高NPP来提高WUE的相应策略可能比采用在控制产量的条件下减少耗水的策略更有效。

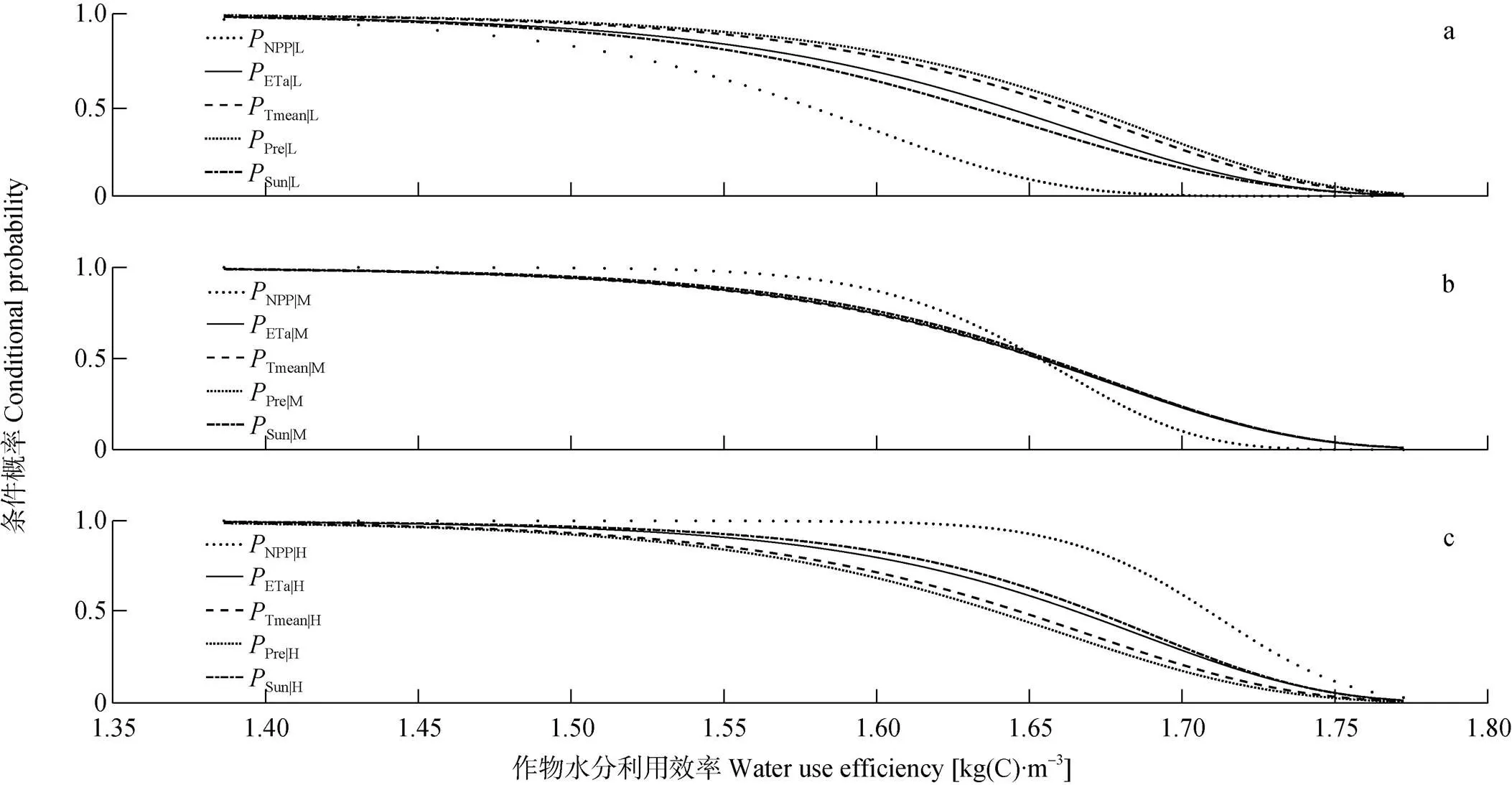
图5 研究区作物水分利用效率受作物净初级生产力(NPP)、作物实际蒸散发(ETa)、年平均气温(Tmean)、年降水量(Pre)和年日照时数(Sun)在低(a)、中(b)、高(c)取值的影响对比

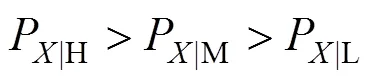
本文采用的WUE被定义为NPP和ETa的比值, 由于WUE是NPP直接计算而来, 两者之间本身存在较大的相关关系。Gilbert等[25]指出在WUE的研究中, 不宜将WUE与作物产出或作物蒸散发建立线性回归, 因为WUE中既包含有作物产出项也包含有作物蒸散发项, 这种形式的线性回归可能会得出不正确的结果。本文基于Copula函数理论的研究方法不需要假设WUE与驱动因子之间存在线性关系或构建特定的多元回归方程, 在WUE的研究中更具有一般性, 给WUE研究提供了新的视角和方法。

虽然WUE直接由NPP和ETa计算而来, 但NPP和ETa观测值对WUE观测值大小的影响方向可以不一致, 比如WUE的提高可能由以下事件导致: 1)NPP提高, ETa减小; 2)NPP提高, ETa不变; 3)NPP提高, ETa提高, 且NPP提高的幅度大于ETa提高的幅度; 4)NPP不变, ETa减小; 5)NPP减小, ETa减小, 且ETa减小的幅度大于NPP减小的幅度。在概率空间中, 并不需要对相关性做出特定要求, 例如事件A包含事件B, 譬如事件A是自然数, 事件B是偶数, 那么事件A和事件B的相关性就很高。但是从概率空间可以判断, 当事件A发生时, 事件B不一定发生; 然而事件B发生了, 事件A就一定发生。采用Copula函数理论来探讨NPP和ET对WUE的驱动, 就是为探讨影响的可能性。

WUE由光合作用和蒸腾作用两个生理过程控制, 且光合作用和蒸腾作用两个过程受到CO2浓度、温度、湿度、光照强度等影响, 动态响应机制十分复杂, 而且作物叶片的光合作用与蒸腾作用在对驱动因子的响应过程中有趋同性, 很难确定两个过程分别处于什么状态会使WUE最优[26]。本文通过条件概率分析了NPP、ETa、Tmean、Pre和Sun不同取值大小对京津冀平原耕地WUE的影响, NPP越大则WUE大于任一特定取值的可能性越大, 且效果较其他变量明显, 说明在京津冀平原采用提高NPP的相应策略来提高WUE可能更有效。京津冀地区面临严重的水资源短缺问题, 根据本文的结论, 在缓解地区水资源压力时并不能单独以提高WUE作为水资源管理的目标, 而应当在控制水资源用量的基础上进一步实现高效用水, 这与水利部于2016年发布的《京津冀协同发展水利专项规划》工作方针是一致的, “节水优先、空间均衡、系统治理、两手发力” “以水资源水环境承载力为刚性约束, 以水资源高效循环利用为前提”。

[1] 鲍超, 贺东梅. 京津冀城市群水资源开发利用的时空特征与政策启示[J]. 地理科学进展, 2017, 36(1): 58–67 BAO C, HE D M. Spatiotemporal characteristics of water resources exploitation and policy implications in the Beijing-Tianjin-Hebei Urban Agglomeration[J]. Progress in Geography, 2017, 36(1): 58–67

[2] 杜朝阳, 于静洁. 京津冀地区适水发展问题与战略对策[J]. 南水北调与水利科技, 2018, 16(4): 17–25 DU C Y, YU J J. Issues on the sustainable development of Beijing-Tianjin-Hebei Region based on the limited water resources[J]. South-to-North Water Transfers and Water Science & Technology, 2018, 16(4): 17–25

[3] ZHANG X L, REN L, WAN L. Assessing the trade-off between shallow groundwater conservation and crop production under limited exploitation in a well-irrigated plain of the Haihe River basin using the SWAT model[J]. Journal of Hydrology, 2018, 567: 253–266

[4] 王学, 李秀彬, 辛良杰. 河北平原冬小麦播种面积收缩及由此节省的水资源量估算[J]. 地理学报, 2013, 68(5): 694–707 WANG X, LI X B, XIN L J. Impact of the shrinking winter wheat sowing area on agricultural water consumption in the Hebei Plain[J]. Acta Geographica Sinica, 2013, 68(5): 694–707

[5] 尚松浩, 蒋磊, 杨雨亭. 基于遥感的农业用水效率评价方法研究进展[J]. 农业机械学报, 2015, 46(10): 81–92 SHANG S H, JIANG L, YANG Y T. Review of remote sensing-based assessment method for irrigation and crop water use efficiency[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(10): 81–92

[6] 冯保清. 我国不同尺度灌溉用水效率评价与管理研究[D]. 北京: 中国水利水电科学研究院, 2013 FENG B Q. Study on the evaluation and management of irrigation water use efficiency for different scales in countrywide[D]. Beijing: China Institute of Water Resources & Hydropower Research, 2013

[7] MO X G, LIU S X, LIN Z H, et al. Regional crop yield, water consumption and water use efficiency and their responses to climate change in the North China Plain[J]. Agriculture, Ecosystems & Environment, 2009, 134(1/2): 67–78

[8] GUO R P, LIN Z H, MO X G, et al. Responses of crop yield and water use efficiency to climate change in the North China Plain[J]. Agricultural Water Management, 2010, 97(8): 1185–1194

[9] MO X, LIU S, HU S, et al. Sensitivity of terrestrial water and carbon fluxes to climate variability in semi-humid basins of Haihe River, China[J]. Ecological Modelling, 2017, 353: 117–128

[10] SUN S B, SONG Z L, WU X C, et al. Spatio-temporal variations in water use efficiency and its drivers in China over the last three decades[J]. Ecological Indicators, 2018, 94: 292–304

[11] 赵姜, 孟鹤, 龚晶. 京津冀地区农业全要素用水效率及影响因素分析[J]. 中国农业大学学报, 2017, 22(3): 76–84 ZHAO J, MENG H, GONG J. Measurement of total factor agricultural water efficiency and analysis of influential factors in Jing-Jin-Ji area[J]. Journal of China Agricultural University, 2017, 22(3): 76–84

[12] 陈洪斌. 我国省际农业用水效率测评与空间溢出效应研究[J]. 干旱区资源与环境, 2017, 31(2): 85–90 CHEN H B. Provincial agricultural water use efficiency evaluation and spatial spillover effect in China[J]. Journal of Arid Land Resources and Environment, 2017, 31(2): 85–90

[13] 桑燕芳, 王中根, 刘昌明. 水文时间序列分析方法研究进展[J]. 地理科学进展, 2013, 32(1): 20–30 SANG Y F, WANG Z G, LIU C M. Research progress on the time series analysis methods in hydrology[J]. Progress in Geography, 2013, 32(1): 20–30

[14] 郭生练, 闫宝伟, 肖义, 等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文, 2008, 28(3): 1–7 GUO S L, YAN B W, XIAO Y, et al. Multivariate hydrological analysis and estimation[J]. Journal of China Hydrology, 2008, 28(3): 1–7

[15] 熊立华, 郭生练, 肖义, 等. Copula联结函数在多变量水文频率分析中的应用[J]. 武汉大学学报: 工学版, 2005, 38(6): 16–19 XIONG L H, GUO S L, XIAO Y, et al. Application of copulas to multivariate hydrological frequency analysis[J]. Engineering Journal of Wuhan University, 2005, 38(6): 16–19

[16] SALVADORI G, DE MICHELE C. Multivariate multiparameter extreme value models and return periods: A copula approach[J]. Water Resources Research, 2010, 46(10): 219–233

[17] HAO Z C, HAO F H, SINGH V P, et al. Quantitative risk assessment of the effects of drought on extreme temperature in eastern China[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(17): 9050–9059

[18] MADADGAR S, AGHAKOUCHAK A, FARAHMAND A, et al. Probabilistic estimates of drought impacts on agricultural production[J]. Geophysical Research Letters, 2017, 44(15): 7799–7807

[19] 李浩鑫, 邵东国, 尹希, 等. 基于主成分分析和Copula函数的灌溉用水效率评价方法[J]. 农业工程学报, 2015, 31(11): 96–102 LI H X, SHAO D G, YIN X, et al. Evaluation method for irrigation-water use efficiency based on principle component analysis and Copula function[J]. Transactions of the CSEA, 2015, 31(11): 96–102

[20] ZHAO Y, ZHANG J P, XIAO W H. Study on the joint probability distribution of irrigation water volume and irrigation water efficiency[J]. Water Science & Technology: Water Supply, 2015, 15(4): 802–809

[21] MO X G, CHEN X J, HU S, et al. Attributing regional trends of evapotranspiration and gross primary productivity with remote sensing: a case study in the North China Plain[J]. Hydrology and Earth System Sciences, 2017, 21(1): 295–310

[22] SADEGH M, RAGNO E, AGHAKOUCHAK A. Multivariate copula analysis toolbox (MvCAT): describing dependence and underlying uncertainty using a Bayesian framework[J]. Water Resources Research, 2017, 53(6): 5166–5183

[23] ZHANG L, SINGH V P. Bivariate flood frequency analysis using the copula method[J]. Journal of Hydrologic Engineering, 2006, 11(2): 150–164

[24] MO X G, LIU S X, MENF D J, et al. Exploring the interannual and spatial variations of ET and GPP with climate by a physical model and remote sensing data in a large basin of Northeast China[J]. International Journal of Climatology, 2014, 34(6): 1945–1963

[25] GILBERT M E, HERNANDEZ M I. How should crop water-use efficiency be analyzed? A warning about spurious correlations[J]. Field Crops Research, 2019, 235: 59–67

[26] 姜寒冰, 张玉翠, 任晓东, 等. 作物水分利用效率研究方法及尺度传递研究进展[J]. 中国生态农业学报, 2019, 27(1): 50–59JIANG H B, ZHANG Y C, REN X D, et al. A review of progress in research and scaling-up methods of crop water use efficiency[J]. Chinese Journal of Eco-Agriculture, 2019, 27(1): 50–59

Analysis of water use efficiency and driving factors in the Beijing-Tianjin-Hebei Province Plain using the Copula method*

LONG Xuezhi1,2, LIU Suxia1,2**, MO Xingguo1,2, CHEN Xuejuan1,2

(1. Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China; 2. School of Natural Resources and Environment / Sino-Danish College, University of Chinese Academy of Sciences, Beijing 100049, China)

Agricultural irrigation accounts for >65% of water use in the Beijing-Tianjin-Hebei Province Plain. Improving the agricultural water use efficiency will help relieve the pressure on the water resources found in the Beijing-Tianjin-Hebei Plain and promote sustainable development. Based on water use efficiency (WUE), net primary productivity (NPP), and actual evapotranspiration (ETa) from 1980 to 2013 simulated by the VIP model, combined with the annual mean air temperature (Tmean), annual precipitation (Pre), and annual sunshine duration (Sun), the Copula method was used to create five groups of joint probability distributions: WUE and NPP, ETa, Tmean, Pre, and Sun. Conditional probability was calculated based on the hypothesis that WUE was greater than any particular value under low, medium, and high value ranges of each driving factor. The findings showed that the greater the values of NPP, ETa, and Sun, the more likely was WUE to be greater than any particular value. However, the lower the values of Tmean and Pre, the more likely was WUE to be greater than any particular value. The sensitivity of WUE to variation in the value of each driving factor was reflected by the difference of the conditional probability of WUE under high and low value ranges, suggesting that WUE was most sensitive to the variation in the value of NPP followed by those of Sun, ETa, Pre, and Tmean. Comparison of the conditional probabilities of WUE under the same value conditions of NPP, ETa, Tmean, Pre, and Sun showed that a lower NPP clearly suppressed WUE and that improvement in NPP guaranteed a higher value of WUE. Crop WUE is controlled simultaneously by photosynthesis and transpiration, which makes it difficult to ascertain the driving mechanism underlying WUE. Based on the joint probability distribution determined using the Copula method and conditional probability analysis, we concluded that improving NPP when water consumption is controlled may be a more effective strategy than reducing water consumption when grain yield is controlled to adopt in the Beijing-Tianjin-Hebei Province Plain.

Beijing-Tianjin-Hebei Province Plain; Water use efficiency; Driving factors; Copula; VIP model; Net primary productivity (NPP)

K903

2096-6237(2019)12-1833-13

10.13930/j.cnki.cjea.190340

* 国家重点研发计划课题(2016YPC0401402)和国家自然科学基金项目(41471026)资助

刘苏峡, 主要从事水文水资源研究。E-mail: liusx@igsnrr.ac.cn

龙学智, 主要从事水文水资源研究。E-mail: longxz.15s@igsnrr.ac.cn

2019-05-06

2019-08-26

* This study was supported by the National Key Research and Development Plan of China (2016YPC0401402) and the National Natural Science Foundation of China (41471026).

, E-mail: liusx@igsnrr.ac.cn

May 6, 2019;

Aug. 26, 2019

龙学智, 刘苏峡, 莫兴国, 陈学娟. 基于Copula的京津冀平原作物水分利用效率驱动因子分析[J]. 中国生态农业学报(中英文), 2019, 27(12): 1833-1845

LONG X Z, LIU S X, MO X G, CHEN X J. Analysis of water use efficiency and driving factors in the Beijing-Tianjin-Hebei Province Plain using the Copula method[J]. Chinese Journal of Eco-Agriculture, 2019, 27(12): 1833-1845