截锥体头型弹丸低速斜入水实验研究*

罗驭川，黄振贵，高建国，陈志华，侯 宇，郭则庆

（南京理工大学瞬态物理国家重点实验室，江苏 南京 210094）

入水过程是一个十分复杂的物理现象，入水冲击时会产生复杂的瞬态物理问题[1]。弹丸以一定速度进入水面时会产生入水空泡，空泡的形成、扩张、闭合、溃灭等会影响弹丸入水航行的运动特性和流体动力学特性。弹丸低速入水后，涉及到复杂的气液两相流动，其中弹丸头部的结构和大小对其空泡和弹道特性有着重要的影响。

早期对弹丸入水的研究多集中于垂直入水。Wei 等[2]拍摄了球体入水空泡形态的演变过程，计算了球体入水速度变化情况，并预测了球体入水速度的公式。何春涛等[3-4]研究了圆柱体低速入水空泡形态，探讨了多弹体串列和并列情况下入水空泡的演变，分析了并列情况下空泡之间的相互影响和串列情况下多弹体对空泡的影响。闫发锁等[5]分析了圆球倾斜入水的冲击压力，设计装置记录了圆球入水初期的流场状态和表面压力。Nila 等[6]分析了PIV 方法在入水冲击载荷测量方面的应用，将PIV 实验结果与数值模拟结果进行对比，分析了物体入水过程中速度的变化规律。Bao 等[7]基于非线性边界条件的速度势理论，模拟了二维楔形体入水空泡。May[8]进行了运动体垂直入水问题试验研究，讨论了运动体特征尺寸和头部形状对入水空泡生成、发展和闭合的影响。黄振贵等[9]分析了90°锥头弹丸不同入水冲击速度下空泡的闭合方式及其演变过程，讨论了空泡闭合时间、闭合点水深和弹头空泡长度随入水速度的变化规律以及不同水深位置空泡直径的变化规律。

对于倾斜入水研究，主要针对锥头体、圆头体。施红辉等[10]给出了锥头、圆头等钝体入水速度对倾斜入水位移和速度特性的影响，施红辉等[11]还对细长体铁钉开展倾斜入水研究，同时给出了入水角度对倾斜入水位移和速度特性的影响。宋武超等[12]对140°锥头回转体倾斜入水进行了实验研究，分析了入水速度、入水角度对空泡流动特性的影响。路丽睿等[13]、杨衡等[14]均研究了锥头与圆头对弹丸倾斜入水空泡和弹道参数的影响，并得出相应影响规律，结果表明锥角和入水速度的较小变化也会引起入水空泡和弹道参数的较大变化。综合现有的文献，截锥体头型对斜入水空泡及弹道参数的影响文献尚未见报导。

基于此，本文在低速倾斜入水条件下，针对截锥体头型弹丸研究其头部直径大小对入水空泡及弹道特性的影响，从两个不同工况进行对比分析，得出截锥体头型弹丸头部直径大小对入水空泡、俯仰角、运动速度的影响规律，为入水弹丸的设计提供一定的参考依据。

1 实验系统与模型参数

斜入水实验装置示意图如图1，主要包括玻璃水槽、高速摄像机、计算机、光源、导轨、支架、坐标纸、水槽底部防护层等。水槽由15 mm厚的普通玻璃粘制，底部设置防护层，覆盖水槽底部。实验中用导轨引导弹丸下落，前后各采用1 300 W 的广告灯光源照明，用Phantom 高速摄像机以4 100 s-1的拍摄速率对入水空泡的演变过程进行拍摄，实验用水采用自来水。

弹丸模型如图2 所示，模型主要由2 部分组成：头部为截锥体，尾部为圆柱体。模型圆柱体部分长度L均为35 mm，直径D均为7 mm。截锥体与弹丸圆柱部的夹角为60°，截锥体头部直径分别为2 mm，3 mm，4 mm，分别以模型A、模型B、模型C 代称。弹丸材料选用45 号钢。弹丸模型的头部特征如表1 所示。

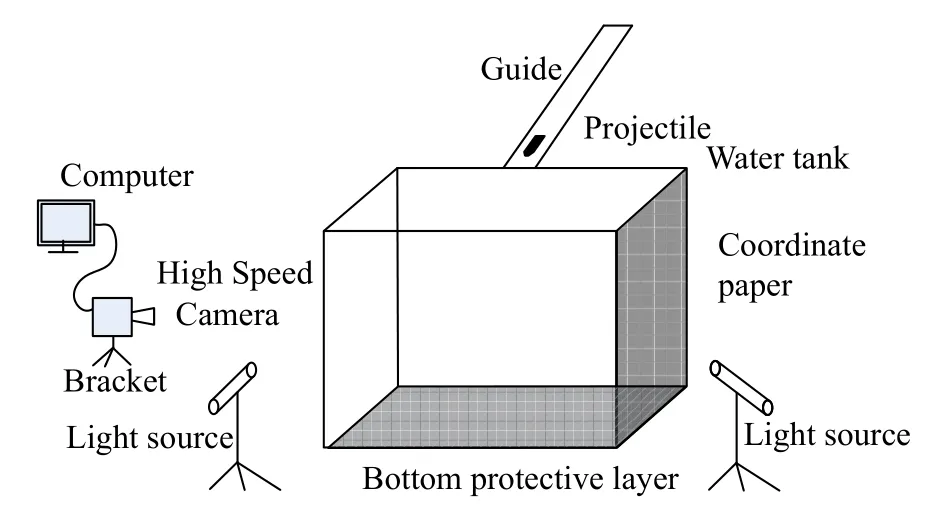
图 1 斜入水实验装置Fig. 1 Experimental device for oblique water entry

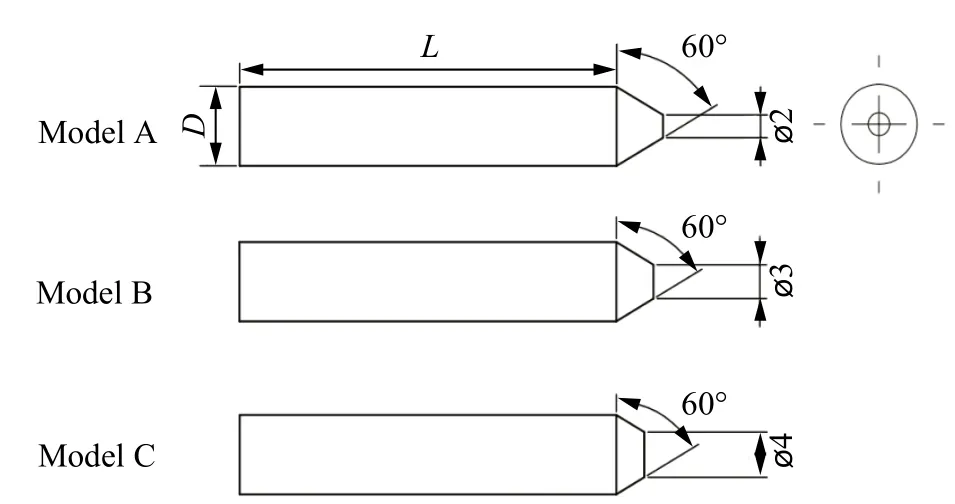
图 2 弹丸模型Fig. 2 Projectile model

表 1 弹丸模型的头部特征Table 1 Head characteristics of projectile model

2 实验结果与分析

2.1 弹丸头部直径大小对入水空泡的影响

利用上述建立的实验测试系统开展了两种工况下弹丸斜入水实验研究，工况1：入水速度u0=3.35 m/s，入水角度θ0=45°；工况2：入水速度u1=3 m/s，入水角度θ1=60°，下文均以工况1 和工况2 来表示。取弹丸头部接触水面时刻作为t=0 的时刻，入水过程中弹丸的航行姿态及空泡演变过程如图3 和图4 所示。

弹丸入水过程经历入水冲击、空泡形成、开空泡、空泡闭合及空泡溃灭5 个阶段。由图3 和图4 可知，在工况1 和工况2 条件下，空泡闭合阶段弹丸尾部均与空泡下壁面发生碰撞，碰撞后由于速度较低弹丸无法修正弹道轨迹，未发生尾拍现象，而是尾部继续与空泡下壁面碰撞，接触面逐渐增大。空泡溃灭阶段时液面处空泡与随体空泡发生分离后，易看出随着接触面的增大，随体空泡被分割为包裹弹体前部的空泡与附着尾部的空泡。

在图3 中，弹丸以工况1 条件下进入水面，模型A、B、C 分别在入水后41.5、37.6、34.6 ms 尾部与空泡发生碰撞。在图4 中，弹丸以工况2 条件下进入水面，模型A、B、C 在入水后40.2、34.2、32.9 ms 尾部与空泡发生碰撞。可知，在两种工况条件下：截锥体头弹丸头部直径越大，尾部越早与空泡下壁面发生碰撞，碰撞均发生在液面空泡与随体空泡分离之前。

图 3 工况1 条件下，弹丸斜入水航行姿态与空泡演变图Fig. 3 Navigation attitude and bubble evolution diagram of projectile obliquely entering water under condition 1

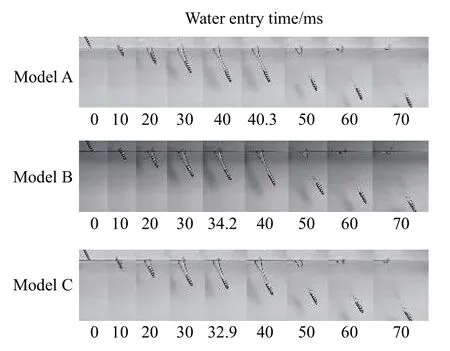
图 4 工况2 条件下，弹丸斜入水航行姿态与空泡演变图Fig. 4 Navigation attitude and bubble evolution diagram of projectile obliquely entering water under condition 2

由实验图测得，模型C 液面处空泡最大，模型B 与模型A 液面处空泡次之，其主要原因在于弹体头部对于流场的扰动，模型A 头部直径最小，入水时截锥体头部侧边曲面较长，对流场扰动能力较小，故液面处空泡长度和大小较小，而模型B 与模型C 头部直径较大，对流场扰动能力较大，故液面处空泡较大。

由图5 和图6 可知，不同头部直径的截锥体头弹丸以工况1 条件入水时液面空泡与随体空泡均于t0=47.3 ms 分离，以工况2 条件下入水时液面空泡与随体空泡均于t1=43 ms 发生分离。可知在两组实验工况下截锥体头部直径大小对空泡闭合时间几乎没有影响，闭合时间主要由入水角和入水速度决定。

图 5 工况1 入水空泡深闭合时刻Fig. 5 Deep closure moment of water entry cavity under condition 1

图 6 工况2 入水空泡深闭合时刻Fig. 6 Deep closure moment of water entry cavity under condition 2

2.2 弹丸头部直径大小对俯仰角的影响

图7 与图8 分别给出了弹丸以工况1 和工况2 条件入水后俯仰角变化曲线，俯仰角是弹体相对于惯性坐标系“俯仰”的角度，即弹体与水平面的夹角。图9 给出了在不同入水阶段，弹丸的简要受力图，O为质心，F1为弹丸头部水平冲击力，F2为弹丸头部铅垂冲击力，F3为浮力，G为重力。

由此可知，模型A 入水过程俯仰角呈逐渐增大的线性规律，而模型B 和模型C 入水过程俯仰角呈先略微增大后减小的非线性规律。主要原因为弹丸在入水碰撞液面时，由于弹丸头部为截锥体型，液面先与弹丸头部前端面及下侧曲面发生碰撞，使得弹丸受到弹丸头部水平冲击力F1，撞击瞬间该冲击力较大，形成了较大的顺时针方向力矩，造成弹丸俯仰角增大，弹丸产生前倾的趋势；当弹丸被空泡完全包裹时，只有弹丸头部与水接触，此时弹丸受到重力G、浮力F3以及头部冲击力F1、F2。因弹丸的质量主要集中在圆柱体部，故3 种模型的弹丸质量近似相同，且均为实心，所以重力和浮力合力近似相同，合力方向均为向下。冲击力F2方向沿铅垂方向向上，抵消部分向下的合力，故头部水平冲击力F1所形成的力矩对弹丸的俯仰运动起主要作用。模型A 截锥体头部侧面面积较大，在入水速度相同的条件下，其受力最大，水平方向冲击力的影响大于重力、浮力以及铅垂方向冲击力合力，故该弹丸产生了顺时针的合力矩。随着截锥体头部侧曲面减小，头部水平冲击力对弹丸俯仰运动的影响逐渐减小，当其作用小于重力、浮力以及铅垂方向冲击力合力的作用时，弹丸合力矩方向变为逆时针，弹丸俯仰角逐渐减小。因模型B 截锥体头部侧曲面比模型C 大，造成模型C 逆时针方向合力矩大于比模型B，故模型C 俯仰角降低较快。此结论印证了2.1 节截锥体头弹丸头部直径越大，尾部越早与空泡下壁面发生碰撞的现象。

图 7 工况1 入水过程俯仰角变化曲线Fig. 7 Variation of elevation angle in water entry process under condition 1

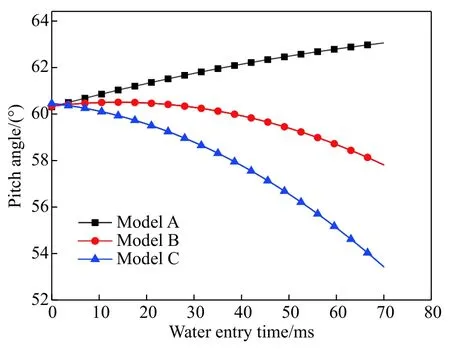
图 8 工况2 入水过程俯仰角变化曲线Fig. 8 Variation of elevation angle in water entry process under condition 2

与工况1 相比，工况2 入水速度小，导致弹丸所受冲击力变小，另外入水角度增加后，导致截锥体所受力在水平向左方向的分量变小。以上均导致工况2 条件下，弹丸俯仰角变化小。

由工况1 与工况2 的俯仰角变化趋势可知，截锥体头部直径大小对入水弹道稳定性有着不可忽视的影响，相比模型A、C，模型B 俯仰角变化较小，偏离直线轨迹程度较小，即弹丸在此实验条件下模型B 的稳定性要优于模型A、C，弹丸头部直径过大或者过小均不利于入水稳定，直径过小会造成俯仰角大幅增大，直径过大会造成俯仰角大幅减小。

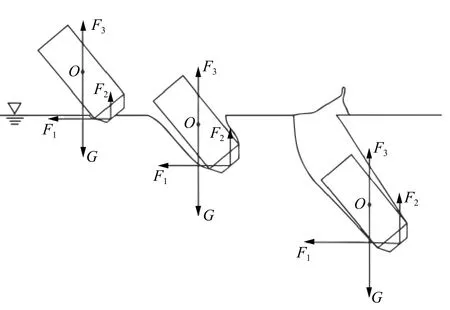
图 9 简要受力分析图Fig. 9 A brief force analysis diagram

2.3 弹丸头部直径大小对速度变化的影响

选取弹头最先接触水面的点为像素获取点，通过对实验入水图进行数据采集获得位移变化曲线，其后对位移曲线求导得到两工况弹头速度随时间变化曲线，如图10、图11 所示。由图可知，工况1 和工况2 弹丸速度变化趋势相反，工况1 条件下弹丸入水后速度均呈下降趋势，而工况2 弹丸入水后速度均呈上升趋势，两工况弹丸速度变化均为线性变化。表明，当初始速度超过该工况的临界速度时，速度变化趋势产生突变，由增大变为减小。

分析受力可知，弹丸受到重力、浮力以及弹丸头部入水后的冲击力。因本文的实验速度较低，冲击力相对较小，冲击力在铅垂方向的分量和浮力之和仍小于重力，此时铅垂方向合力始终向下，加速度始终向下，即弹丸铅垂方向速度始终增加；在冲击力沿水平方向分量的作用下，弹丸水平方向速度始终减小直至减为零。弹丸初速度较低时，铅垂方向速度增加大于水平方向速度减小，合速度呈上升趋势。弹丸初速度增加时，水平方向受到的冲击力会增大，向左加速度增大，水平方向速度衰减加快。因此随着弹丸初始速度的增大，水平方向速度衰减率会逐渐大于铅垂方向速度增加率，合速度最终呈衰减趋势。经多次实验验证，在45°入水角下，当弹丸速度为3.28 至3.30 m/s 时，其合速度变化幅度最小，即在3.28 至3.30 m/s 中存在着某一临界点，在该临界点前后，速度变化呈现出不同的规律。

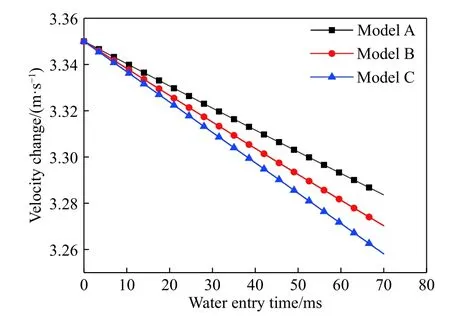
图 10 工况1 速度随时间变化图Fig. 10 Velocity versus time chart under condition 1

图 11 工况2 速度随时间变化图Fig. 11 Velocity versus time chart under condition 2

由图10 可知，模型C 在工况1 中速度衰减最快，模型B 次之，模型A 最慢。分析受力情况可知，由于阻力方向与速度方向相反，各模型前端面是影响弹丸速度的主要受力面，模型C 前端面面积接近模型B 前端面面积的两倍，是模型A 前端面面积的四倍，故模型C 受到的阻力较大，速度衰减最快，模型B 次之，模型A 最慢。可推论得，弹丸入水速度大于临界点时，截锥体头弹丸速度衰减随弹丸头部直径增大变快，为保持入水速度衰减较慢，此时应尽可能选用头部直径较小的弹丸模型。

由图11 可知，模型A 在工况2 中速度上升最快，模型B 次之，模型C 最慢。分析工况条件和受力知，此工况下速度较小，入水角为60°，铅垂方向受力对速度影响较大，由于模型A 头部前端面面积最小，头部铅垂冲击力较小，弹丸受到向下的合力最大，铅垂方向加速度较大，故模型A 速度上升快于模型B、C。由图10 和图11 可推论，在工况2 时，当初始速度增大直至越过其临界值时速度变化亦会突变为衰减趋势。由上文受力分析和实验结果验证亦可知，速度上升是在向下入水的前提下重力大于阻力造成的，如果向上入水，速度只会降低不会上升。临界速度随着入射角的改变而改变，入射角向上，临界速度消失。

韦伯数We为：

式中：v为弹丸初始入水速度，l为弹丸特征长度，一般情况下特征长度取弹丸最大直径，但由于弹丸头部为截锥体，头部侧面和前端面均会对入水产生重要影响，因此可取头部直径与截锥体两条母线长度之和为特征长度l，即模型A、B、C 的特征长度分别为0.012 m、0.011 m、0.01 m， σ 为流体的表面张力系数，取0.075 N/m。

计算得到的韦伯数We如表2 所示，两种工况下各模型的韦伯数均略大于1，这表明，入水过程中，惯性力的作用大于表面张力，但表面张力的作用不可忽视。

由We计算公式可知，工况1 速度大于工况2，所以工况1 同模型的We大于工况2 同模型的We，即速度越大，表面张力的影响越小，故只需讨论同一工况下不同模型的We。两工况中模型A、B、C 的We均依次减小，表面张力的影响依次增大，由于表面张力体现为对弹丸的阻力作用，故工况1 条件下模型A 速度衰减最慢，模型C 速度衰减最快，模型B 处于中间；工况2 条件下模型A 速度增加最快，模型C 速度增加最慢，模型B 处于中间，与文中图10 和图11 速度变化曲线一致。

弗劳德数Fr的计算公式为：

式中：v为弹丸入水的初始速度，l为弹丸特征长度，模型A、B、C 的特征长度分别为0.012 m、0.011 m、0.01 m，g为重力加速度。

计算得到的Fr如表3 所示，Fr小时重力起主导作用，Fr大时惯性力起主导作用。可知，工况1 惯性力起主导作用，速度减小；工况2 重力起主导作用，速度增加。同一工况下，模型A 的Fr最小，模型C 的Fr最大。因此，工况1 条件下模型A 速度衰减最慢，模型C 速度衰减最快，模型B 处于中间；工况2 条件下模型A 速度增加最快，模型C 速度增加最慢，模型B 处于中间，与文中图10 和图11 速度变化曲线一致，由此可证明实验的准确性。当Fr处于某一临界值时，此时惯性力与重力的作用相当，两者对速度的影响相互抵消，此速度为临界速度，具体表现为铅垂方向速度增加的加速度与水平方向速度衰减的加速度对合速度影响刚好抵消。

表 2 韦伯数WeTable 2 Weber number We

表 3 弗劳德数FrTable 3 Froude number Fr

3 结 论

本文基于高速摄影系统研究了截锥体头型弹丸在低速斜入水条件下头部直径大小对入水空泡及弹道特性的影响，对比分析了不同模型低速倾斜入水现象，得到了头部直径大小对截锥体头弹丸入水空泡、运动速度、俯仰角的影响规律，具体结论如下：

（1）截锥体头弹丸头部直径越大，尾部越早与空泡发生碰撞；截锥体头弹丸头部直径大小对空泡闭合时间几乎没有影响；液面处空泡随头部直径增大而增大；

（2）截锥体头弹丸头部直径过大或者过小均不利于入水稳定性；取适中大小头部直径时俯仰角变化较小，入水稳定性高；

（3）当入水角为45°时，截锥体头弹丸如果速度较高，为保持入水速度衰减较小，此时应尽可能选用头部直径较小的弹丸模型。但为保证入水稳定性，头部直径不宜过小，在弹丸设计中需综合考虑头部直径的大小；

（4）当截锥体头弹丸入水速度较低时，弹丸入水速度低于其临界值时，速度呈上升趋势，速度高于临界值时，呈现下降趋势。此临界速度表现为铅垂方向速度增加的加速度与水平方向速度衰减的加速度对合速度影响刚好抵消。弹丸以临界速度入水时，合速度在一定范围内基本保持不变。