基于自适应径向基函数神经网络的光伏MPPT研究
王镇道 郭敬勋 肖旺


摘 要:光伏系统在局部遮阴情况下,输出曲线呈现多峰特性. 针对传统最大功率控制算法易追踪到局部最大功率点的缺陷,提出一种基于自适应径向基函数(Radial Basis Function,RBF)神经网络的控制算法. 该算法以自适应线性算法优化RBF神经网络的扩展常数与权重,克服了传统神经网络算法收敛速度慢、全局寻优差的缺点. 在MATLAB/Simulink环境下建立自适应RBF神经网络仿真模型进行验证,结果表明,提出的算法在外界光照、温度发生变化时能准确找到光伏系统的最大功率点,且在收敛精度和收敛时间上均有很大的提升.
关键词:光伏系统;最大功率点跟踪;自适应;神经网络
中图分类号:TN432 文献标志码:A
Photovoltaic System MPPT Algorithm Based
on Adaptive Radial Basis Function Neural Network
WANG Zhendao,GUO Jingxun?覮,XIAO Wang
(School of Physics and Electronics,Hunan Uiversity,Changsha 410082,China)
Abstract: The power-voltage characteristic curve of photovoltaic system has multiple peaks under partial shade condition. The traditional maximum power tracking method can easily trace to the local maximum power point. To solve such shortcoming,a photovoltaic system Maximum Power Point Tracking(MPPT) algorithm based on adaptive radial basis function neural network is proposed. The model optimizes the extended constants and weights of RBF neural network with adaptive linear algorithm, which overcomes the shortcomings of traditional neural network algorithm with slow convergence speed and poor global optimization. The simulation of adaptive RBF neural network is carried out in MATLAB/Simulink environment. The results show that the proposed algorithm can accurately find the maximum power point of the photovoltaic system when the external illumination and temperature change. Moreover the convergence accuracy and convergence time are greatly improved.
Key words:photovoltaic system;Maximum Power Point Tracking(MPPT);adaptive;neural network
近年来,我国光伏产业发展迅猛,2012年到2015年,光伏发电总装机容量由328万kW增至
3 500万kW. 至今,光伏发电总装机容量超过了100 GW,中国光伏发电累计装机规模已成为全球第一,这表明在我国光伏发电正在从补充性能源向替代能源过度[1].
光伏发电中亟待解决的一项关键问题就是最大功率点跟踪(Maximum Power Point Tracking,MPPT). 目前,国内外学者提出许多方法:扰动观察法及其改进方法[2-4]、电导增量法及其改进方法[5-7]、基于外部环境参数模型的定电圧法[8]、 参数整定法[9]、模糊控制法[10]等. 然而,在遮阴情况下,光伏系统的P-V特性呈现为具有多个极值的曲线,上述方法在该情况下易找到局部最大值. 对此,有学者提出根据电流特性跟踪最大功率点的算法以及根据粒子群多峰查找的优势,提出粒子群算法,上述算法查找时需要不断改变电流或者电压,根据后续变化来确定下一步动作,延时高,且浪费能量. 也有学者提出分布式光伏发电[11],然而该方法增加了硬件电路的成本. 近年来,神经网络控制算法被越来越多应用到光伏系统最大功率追蹤上,神经网络具有很好的学习能力和识别能力,可以很好地逼近光伏系统的最大功率
点[12-13]. 本文提出了一种基于自适应RBF神经网络的光伏系统MPPT控制算法. 基于神经网络的MPPT算法通过采集多组温度、光照强度和最大功率点电压数据,在已建立的神经网络模型训练后,可根据外界环境变化直接预测出最大功率点电压,无需多次改变电路中电压或者电流值,有效地提高了光伏系统的效益.
1 光伏发电系统
1.1 光伏电池模型
常用的单晶硅光伏电池通常可以用单二极管模型如图1所示来表示,其输出如式(1)所示[14]:
■
图1 单二极管光伏电池模型
Fig.1 PV cell of single diode
Ipv = Iph - Io(e■-1)-V+Ipv Rs /Rsh (1)
式中:Iph为光生电流;Io为二极管反向饱和电流;q为电子电荷;n为二极管理想因子;K为玻尔兹曼常数;T为光伏电池绝对温度;Rs和Rsh分别为光伏电池内部等效串并联电阻;V为输出电压. 式(1)中等式左右均含有Ipv,且参数过多,工程实用价值不高. 故本文使用光伏电池工程模型[15]. 具体公式如式(2)(3)所示:
I = Isc{1 - Ct1[exp(V/Ct2Voc)-1]}Ct2 = (Vm /Voc - 1)/ln(1 - Im /Isc)Ct1 = (1 - Im /Isc)exp(-Vm /C2Voc) (2)
ΔT = T - TrefΔS = S/Sref - 1Isc1 = Isc S/Sref(1 + aΔT)Voc1 = Voc(1 - cΔT)(1 + bΔS)Im1 = Im S/Sref(1 + aΔT)Vm1 = Vm(1 - cΔT)(1 + bΔS) (3)
式中:Tref = 25 ℃;Sref = 1 000 W/m2;a = 0.002 5/℃;b = 0.5 ℃;c = 0.002 88/℃.
1.2 光伏电池输出特性
在MATLAB/Simulink上建立光伏电池工程模型,仿真得到在不同温度、光照强度下光伏电池的输出特性曲线. 其中光伏电池的电气参数如下:开路电压44.2 V,短路电流5.2 A,最大功率点电压35.2 V,最大功率点电流4.95 A. 不同温度和不同光照强度下光伏电池输出特性曲线如图2所示.
根据图2光伏电池输出特性曲线可知,光伏电池输出在环境一定时存在唯一的最大功率点. 在温度一定时,光伏电池最大功率和最大功率点电压随着光照强度增加而变大;在光照强度一定时,光伏电池最大功率和最大功率点电压随着温度减小而变大,且光伏电池的最大功率点随着外界环境是一个动态变化的非线性过程,所以追踪最大功率点的精度和速度是很有意义的.
■
电压/V
(a)同一光照强度不同温度下输出特性曲线
■
电压/V
(b)同一温度不同光照强度下输出特性曲线
图2 光伏电池输出特性曲线
Fig.2 Photovoltaic cell output characteristic
2 基于自适应RBF的MPPT
2.1 RBF神经网络
RBF神经网络是由Mondy和Darken于1989年提出的,是一种对非线性函数具有一致逼近能力的新型神经网络结构. 径向基神经网络包括3层网络结构,分别为输入层、隐含层、输出层,它是一种将输入矢量映射到高维空间的神经网络学习方法. 构成RBF神经网络的基本思想是:以RBF函数搭建隐含层空间,通过选定RBF函数的中心来确定输入矢量至隐空间的映射关系,输出层即RBF神经网络结构的输出由隐含层各神经元的线性加权和确定. 总体来看,神经网络的输入与输出是非线性的,而输出对可调权重是线性的,从某种特殊意义来看,高维空间更可能是线性可分的.
图3为RBF神经网络结构示意图. 输入层将
■
图3 RBF神经网络结构示意图
Fig.3 Neural network structure diagram
输入矢量转换为信号源节点传递到隐含层,隐含层由径向基函数构成,将输入信号转化并作为输出层的输入传递到输出神经元,神经网络结构的输出量即为各神经元的线性加权和.
2.2 自适应RBF神经网络的学习过程
在本文中采用自适应RBF神经网络作为MPPT训练方法,RBF神经网络主要由3部分构成,分别为:输入层、隐含层、输出层. 其中输入层到隐含层之间由高斯函数构成,隐含层到输出层由各层间的权重和构成. RBF神经网络输入层到隐含层采用高斯函数输出关系如式(4)所示:
φi(x) = exp-■ (4)
式中: i为第i个神经元;x为n维输入向量;φi(x)为隐含层输出;ci为基函数即高斯函数的中心;δi为扩展常数.
RBF神经网络的隐含层到输出层采用线性权重和构成,输出层与隐含层的关系如式(5)所示:
u(i) = ■wi φi(x) (5)
式中:u为输出层神经元的输出;wi 为连接网络隐含层和输出层的权值.
在RBF网络中,训练速度取決于高斯函数的中心、扩展常数和隐含层到输出层的连接权值,当隐含层神经元个数与高斯函数中心等参数确定后,对连接权值优化就可得到很快的训练速度.
自适应神经网络具有在线、实时和可调节的特点,可根据系统误差等激励函数更快地逼近问题最优解. 自适应神经网络控制算法设计主要有2种方法,一是通过系统设计研究问题数学模型,再根据模型指标进行自适应设计;二是根据神经网络预测误差函数直接调节神经网络内部学习参数,通过动态有监督的实时控制网络学习参数更快地逼近系统最优解. 本文采用第2种方法,通过建立神经网络的误差代价函数直接调节神经网络的权重值与扩展常数,大大减小神经网络的学习训练次数.
代价函数定义为RBF神经网络训练输出与实际值的误差平方和,如式(6)所示:
J = ■■[ y(i) - u(i)]2 (6)
其中 y(i)为实际值. 为取得代价函数极小值,可采用高效的梯度下降法来实现. 为减小计算成本,加快收敛速度,避免梯度下降进入局部最优点,本文采用随机梯度下降法. 采用随机梯度下降法每次迭代只计算训练样本的单个数据,其中权值和扩展常数的更新策略如式(7)(8)所示:
wi = wi-1 + ΔwΔw = η1■ = η[ y(i) - u(i)]φi(x)η1 = cepo-c21 (7)
δi = δi-1 + ΔδΔδ = η2■[ y(i) - u(i)]φi(x)(x - ci) (8)
式中:η1为随时间变化的自适应学习速率;η2为学习速率;epo为迭代次数;c1、c2均为常数.
2.3 各网络层节点设计
1)确定学习样本. 本文在MPPT追踪过程中,以光伏电池外界环境温度T和光照强度S以及对应最大功率点电压为学习样本数据,共计350组.
2)建立自适应RBF神经网络. 根据学习样本数据以及多次试验分析,確定输入层神经元2个,隐含层神经元8个,输出层神经元1个.
3)各参数初始化设计. 学习速率、初始化权值、扩展常数、中心初始化如表1所示.
表1 神经网络初始化参数
Tab.1 Neural network initialization parameter
■
3 仿真分析
本文试验数据由广州三晶电气生产的光伏板进行试验测试所得,采样温度、光照强度、最大功率点电压共计300组数据,其中270组作为学习样本数据,30组作为目标样本数据,以验证神经网络输出的准确性. 设定自适应RBF神经网络最大训练次数200次,训练期望误差0.000 1.
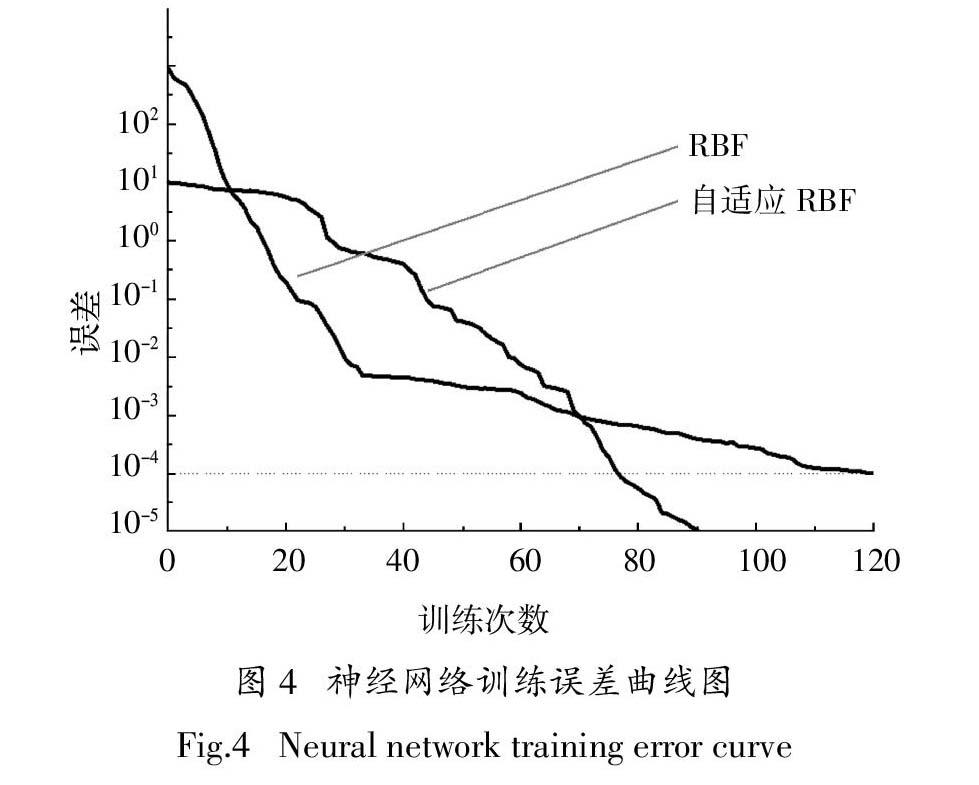
通过MATLAB对自适应RBF神经网络与直接计算法RBF神经网络编程设置,2种神经网络训练误差图如图4所示,从图中明显可以看出,当达到期望误差值0.000 1时,基于自适应RBF神经网络训练需要76步,与直接计算法RBF神经网络需要121步相比较,可明显看出,自适应RBF神经网络的MPPT具有更快的收敛特性与逼近效果.
■
训练次数
图4 神经网络训练误差曲线图
Fig.4 Neural network training error curve
为了评估神经网络模型预测准确性,通过设置自适应RBF神经网络在训练次数80次后,测试目标样本数据. 误差评价函数采用实际电压与预测电压之间差值以直观观察训练结果,预测电压误差如图5所示. 从图5可看出,经自适应RBF神经网络训练后,30个样本数据的预测电压与实际MPP电压的误差为-0.01~0.01,使用MATLAB中的MSE函数计算,训练后数据均方误差MSE为9.254 1×10-5,达到了较高的预测精度.
■
采样点个数
图5 神经网络预测电压误差曲线图
Fig.5 Neural network prediction voltage error curve
由图4和图5可知,基于RBF神经网络的MPPT控制算法在训练过程中通过不断动态优化神经网络控制参数,有效地提高了训练效率及训练精度. 与直接计算法RBF神经网络对比,可明显看出自适应RBF神经网络具有更高的学习速度与更快的逼近路线,通过对样本数据的预测,自适应RBF神经网络也具有很好的预测精度.
4 结 论
本文分析光伏系统在外界不同温度和光照强度下最大功率点非线性变化的基础上,提出了一种基于自适应RBF神经网络的光伏系统最大功率算法. 仿真试验表明,通过训练过程中不断自适应优化神经网络的权值和扩展常数,自适应RBF神经网络MPPT可克服传统神经网络算法收敛速度慢、容易陷入局部最优点等缺点,有效提高了光伏系统最大功率点的预测速度及预测精度,在一定程度上提升了光伏系统发电的效率和性能.
参考文献
[1] 周华安,孟志强,王保田. 光伏发电系统MPPT固定频率滑模控制[J]. 湖南大学学报(自然科学版),2015,42(10):97—101.
ZHOU H A,MENG Z Q,WANG B T. Fixed-frequency-sliding-mode controller used in photovoltaic system MPPT[J]. Journal of Hunan University(Natural Sciences),2015,42(10):97—101.(In Chinese)
[2] PENG L L,XU W,LI L M,et al. An improved perturb and observe algorithm for photovoltaic motion carriers[J]. Materials Science and Engineering,2018,322:072028.
[3] SELLAMI A,KANDOUSSI K,OTMANI R E,et al. A novel auto-scaling MPPT algorithm based on perturb and observe method for photovoltaic modules under partial shading conditions[J]. Applied Solar Energy,2018,54(3):149—158.
[4] MANGANIELLO P,RICCO M,PETRONE G,et al. Optimization of perturbative PV MPPT methods through online system identification[J]. IEEE Transactions on Industrial Electronics,2018,61(12):6812—6821.
[5] 周东宝,陈渊睿. 基于改进型变步长电导增量法的最大功率点跟踪策略[J]. 电网技术,2015,39(6):1491—1498.
ZHOU D B,CHEN Y R. Maximum power point tracking strategy based on modified variable step-size incremental conductance algorithm[J]. Power System Technology,2015,39(6):1491—1498. (In Chinese)
[6] HUYNH D C ,DUNNIGAN M W. Development and comparison of an improved incremental conductance algorithm for tracking the MPP of a solar PV panel[J]. IEEE Transactions on Sustainable Energy,2016,7(4):1421—1429.
[7] SHAHID H,KAMRAN M,MEHMOOD Z,et al. Implementation of the novel temperature controller and incremental conductance MPPT algorithm for indoor photovoltaic system[J]. Solar Energy,2018,163:235—242.
[8] TAFTI H D,MASWOOD A I,KONSTANTINOU G,et al. A general constant power generation algorithm for photovoltaic systems[J]. IEEE Transactions on Power Electronics,2018,33(5):4088—4101.
[9] 李星碩,文辉清. 基于b参数的变步长MPPT控制研究[J]. 电力系统保护与控制,2016,44(17):58—63.
LI X S,WEN H Q. Research on an improved b-based variable step MPPT algorithm[J].Power System Protection and Control,2016,44(17):58—63. (In Chinese)
[10] El-KHATEB A,RAHIM N A,SELVARAJ J,et al. Fuzzy-logic-controller-based SEPIC converter for maximum power point tracking[J].IEEE Transactions on Industry Applications,2014,50(4):2349—2358.
[11] MOON S,YOON S G,PARK J H. A new low-cost centralized mppt controller system for multiply distributed photovoltaic power conditioning modules[J]. IEEE Transactions on Smart Grid,2017,6(6):2649—2658.
[12] MESSALTI S,HARRAG A,LOUKRIZ A. A new variable step size neural networks MPPT controller: review,simulation and hardware implementation[J]. Renewable and Sustainable Energy Reviews,2017,68:221—233.
[13] HARRAG A,BAHRI H. Novel neural network IC-based variable step size fuel cell MPPT controller: performance,efficiency and lifetime improvement[J]. International Journal of Hydrogen Energy,2017,42(5):3549—3563.
[14] REZK H,HASANEEN E S. A new MATLAB/Simulink model of triple-junction solar cell and MPPT based on artificial neural networks for photovoltaic energy systems[J]. Ain Shams Engineering Journal,2015,6(3):S2090447915000404.
[15] KRISHNA D S G,RAVALI M. An intelligent MPPT controller for a PV source using cascaded artificial neural network controlled DC link[C]//International Conference on Signal Processing. Chengdu,2016:983—988.

