队形识别智能化方法定量分析

田立业,刘 剑，鲍 凯

(海军潜艇学院,山东 青岛 266100)

潜艇战术应用软件的研究、开发、使用已经有多年的历史[1]。潜艇战术应用软件实现潜艇辅助指挥决策、情报综合处理和武器综合控制等功能。多年的积累和进步使得潜艇战术应用软件日臻成熟,在战斗和训练中发挥了越来越重要的作用。战术软件中态势推理和决策等部件中会用到队形判断功能,也就是自动判断敌舰艇编队属于哪种队形。已知的判断方法有：基于模板匹配的方法[2],基于领域知识的线型队形识别[3],基于神经网络的方法[4],以及纯数学解析法等。其中,基于神经网络的方法在处理数据的过程中表现出很好的模糊性和鲁棒性,智能化程度和识别正确率很高[5]。

近些年来,人工智能和深度学习技术在模式识别等领域有了突飞猛进的研究进展[6-8],软硬件消费市场上涌现出智能音箱、语音APP等大量成熟的产品,谷歌AlphaGo和苹果Siri更是成功吸引了人们的目光,今后一个时期内也必将得到更多的关注和应用。2019年3月，美国计算机协会ACM宣布把2018年的图灵奖颁给Yoshua Bengio等三名人工智能科学家[9]。潜艇战术应用软件在这场变革大潮中也面临一个重大的技术跨越,从以往单纯靠既定规则和公式得到输出结果升级为依靠智能化方法通过黑盒计算得到结果。智能化方法的应用已经得到了简单的定性论证,还需要定量多维度地开展研究和试验,得到更多更详细的数据,来帮助我们准确地设计研发潜艇战术应用软件。

1 智能化方法

要实现一定程度的人工智能,研究人员往往会把目光放到深度学习、卷积神经网络、强化学习等这些近年来表现抢眼的研究热点上来,实际上简单的队形识别问题属于一个小规模的模式识别问题,且样本特征容易提取,文献[5]已经证明普通神经网络就可以实现较好的识别效果。

径向基函数(Radial Basis Function,RBF)是Powell教授为解决多变量插值问题首先提出的。1988年,Broomhead等人将RBF应用于自适应神经网络的设计中构成了RBF神经网络。1990年,Poggi和Giriosi发表了两篇重要的学术论文,将正则化理论应用于RBF神经网络,对RBF神经网络的理论与设计做出了重要贡献。径向基函数神经网络RBF在逼近能力、分类能力和学习速度等方面均优于BP神经网络,收敛速度快,无局部极小。图1～3展示了径向基网络的结构。

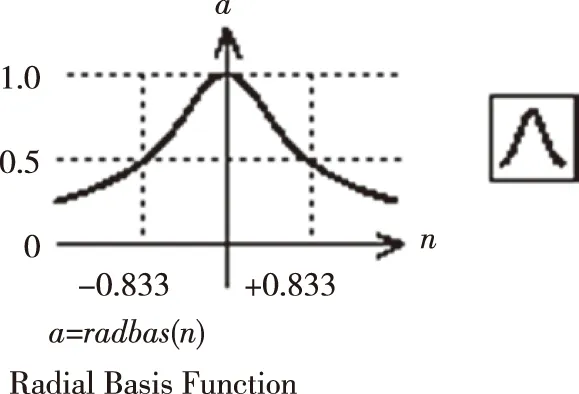
图1 径向基函数的图形和符号

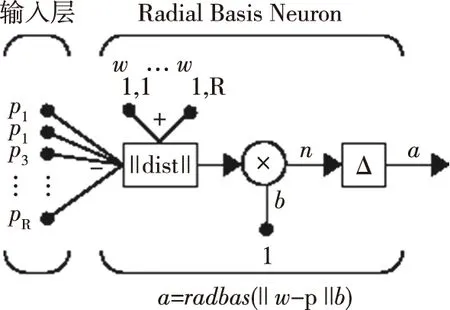
图2 径向基神经网络的神经元结构图

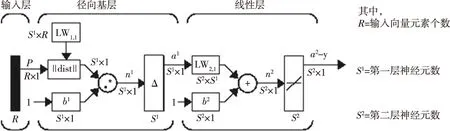
图3 径向基函数网络结构图

径向基网络在创建时又分两种方式：近似的RBF网络和精确的RBF网络。近似的RBF创建之初没有神经元,在训练迭代中逐步增加神经元个数,调整线性层权值,直至达到误差或者神经元数目的阈值。精确的RBF是指零误差的网络,这种神经网络神经元数等于输入样本数量,创建速度快,网络直接记忆了每一个训练样本,且是精准无误差的。

本文的试验中引入两种变形的RBF神经网络,广义回归神经网络GRNN和概率神经网络PNN[10]。图4中,GRNN建立在非参数回归的基础上,以样本数据为后验条件,执行Parzen非参数估计,依据最大概率原则计算网络输出。GRNN建模需要的样本数量少,有些重要的参数不需要人为确定,减少了人为干扰因素。图5中，概率PNN融合了密度函数估计和贝叶斯决策理论,在某些容易满足的条件下,以PNN实现的判别边界渐进地逼近贝叶斯最佳判定面,每一个训练样本确定一个隐含层神经元,神经元的权值直接取自输入样本值,训练容易,适用于实时处理。PNN各层神经元的数目比较固定,易于硬件实现,它的扩充性能好,增加或者减少模式数量时不需要重新进行长时间的训练。

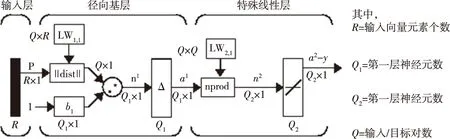
图4 GRNN结构

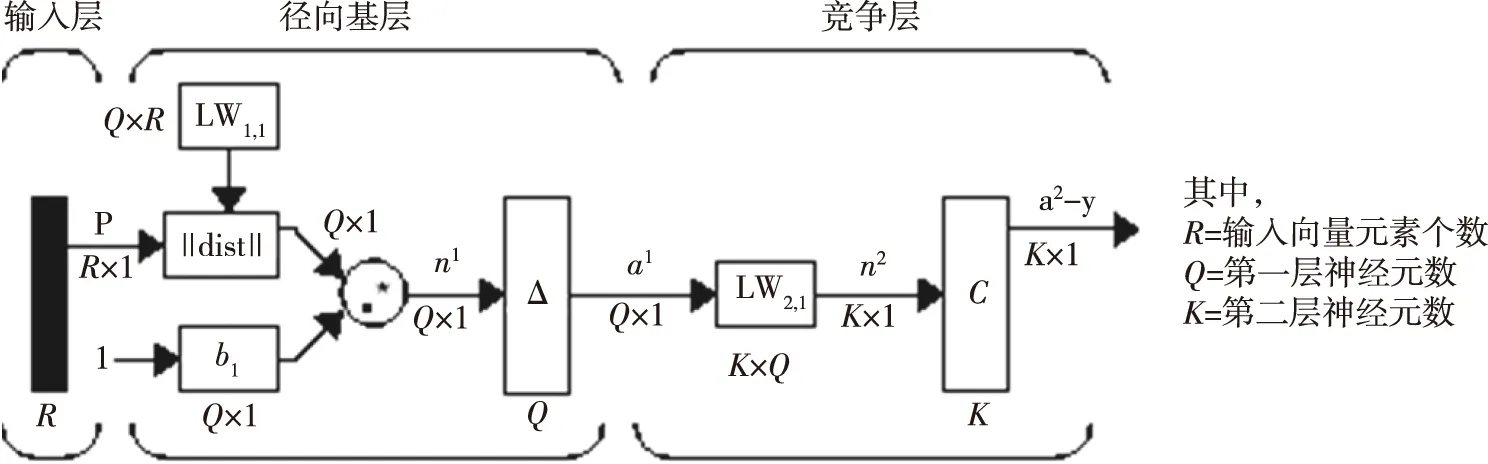
图5 PNN结构

本文拟对以上4种人工神经网络进行试验对比:1)近似的RBF网络,简称RBF;2)精确的RBF,简称RBFE;3)广义回归神经网络,简称GRNN;4)概率神经网络,简称PNN。

2 试验数据的获取

在雷达等传感器所获得的对方舰艇的位置信息中,目标位置信息通常是以经纬度或者方位距离的形式给出。经纬度可用于全球定位,以全球的坐标为背景来研究某一舰艇编队的队形显然不合适,棋盘太大，阵势太小,坐标前几位相同只有后几位有区别。因此,将舰艇编队中所有的舰艇按照其位置和相对位置放置到一个10×10的棋盘上,棋盘的一条边表示横坐标,相邻一边表示纵坐标,无舰艇的位置用白色表示,有舰艇的位置用黑色表示。即使目标数量少间距大,用图像处理算法将其膨胀放大,最终可以饱满地置于这个棋盘上,等比例缩放显然不影响队形识别的结果。在计算机中可以用一个10×10的二维矩阵表示该样本,为了避免归一化处理增加试验的复杂程度,选用0和1作为标记符号,无舰艇的位置元素为0,有舰艇的位置元素为1,如图6所示。

图6 队形的表示

Matlab软件能够方便快捷地处理数据,而且其中的工具箱Deep Learning Toolbox可以对神经网络进行试验,选为我们的试验环境。Matlab版本R2018b,Deep Learning Toolbox版本12.0。图中的二维矩阵在Matlab中转化为一维数组送入神经网络进行训练和仿真,转换规则人为规定为先取出矩阵的第一列数据,再取出第二列拼接到第一列之后,依次进行直至取出全部十列,10×10的矩阵就转换成了100×1的矩阵,也就是一个1元数组,即可以送入网络处理。离线训练和在线仿真时都采用这种处理方法。

常用的模式识别试验方法是将样本集中所有的样本二八分,80%置于训练集,20%置于测试集,多轮试验的时候每一轮百分比相同而分法不同,这种方法可以科学有效地考察该模式识别方法的识别能力。本文所研究的这个具体问题是离线时将神经网络训练好,潜艇训练时或者战时在线地调用它得到结果,更注重考察神经网络的泛化能力而非识别能力,故而采用另一种方法:分别人为地准备训练集样本和测试集样本,训练集样本采用相对理想的样本,测试集样本采用带有一定误差的样本。以此来分别模拟实验室环境和真实环境,真实环境中传感器获取数据和后期的数据处理都会引入一定误差,所谓“一定误差”是指样本跟真实数据和理想数据都有少量区别。因而训练集样本和测试集样本数量要少,便于细微地调整试验内容进行较为精致的试验。

本文按照这些方法和原则准备样本数据,在不同的神经网络上反复试验对比。

3 试验过程

首先我们准备数据和网络,按照前述方法准备图7所示 9个训练样本。

为了便于在训练时设置目标向量和在仿真后直观地观察结果,用数字给队形编号,规定横队队形编号为1,纵队队形编号为2,人字队队形编号为3。处理完成的9个训练样本按照“横横横纵纵纵人人人”的顺序放入训练集,则目标向量为[1 1 1 2 2 2 3 3 3],可以使用ind2vec和vec2ind函数将编号和向量互转，分别调用神经网络工具箱中的四种函数建立和训练四种神经网络:newrb、newrbe、newgrnn、newpnn。训练完成后的网络结构参数如图8所示。

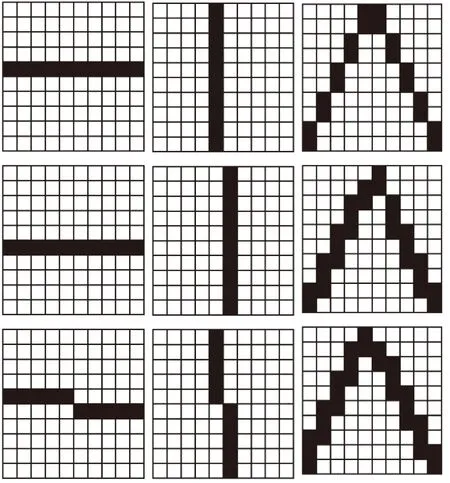
图7 训练集样本

图8 训练完成后的四种神经网络

3.1 试验1

按照图9准备的3个测试样本,每个样本与训练样本接近但不完全相同,以此测试网络的泛化能力,样本置入测试集后用sim函数对4个神经网络进行仿真。

图9 测试集

仿真的正确结果是[1 2 3],试验结果见表1。

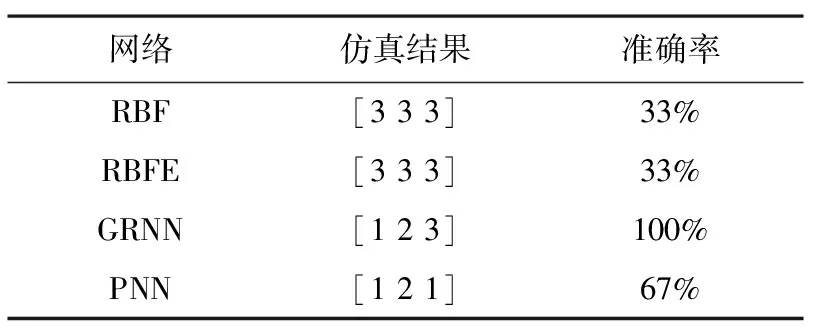
表1 试验1结果

3.2 试验2

我们在试验1的基础上将训练集翻倍,即训练集中的样本内容不变,每个样本在训练集中出现两次,测试集不变的情况下试验结果见表2。

表2 试验2结果

3.3 试验3

按照图10准备3个样本置入第2个测试集,其中前两个样本来自训练集,第3个样本比起前一个测试集来说更加接近于训练集样本。

本文用此测试集分别测试4个神经网络,试验结果见表3。

表3 试验3结果

3.4 试验4

试验4增加反人字队队形,队形编号设置为4,训练样本如图11所示,样本添加至训练集,测试集也相应地增加图12所示第4个测试样本。

用新的训练集同样地构建训练4个神经网络,查看训练完成的RBF网络,如图13所示,其结构不变,神经元数发生改变。

用新的测试集测试效果,正确结果应为[1 2 3 4],将训练集送入网络后仿真的输出结果见表4。

表4 试验4结果

图10 测试集

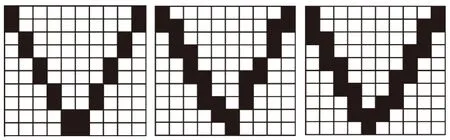
图11 反人字队训练集

图12 反人字队测试样本

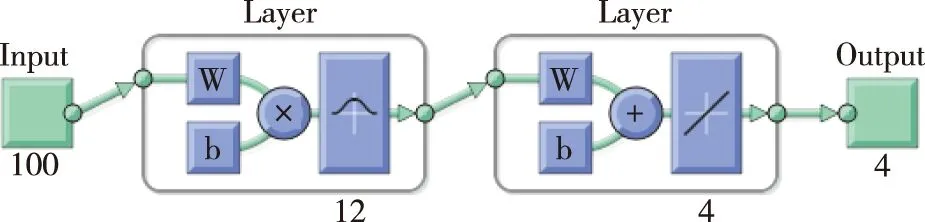
图13 训练完成后的RBF网络

4 结果分析及结论

1)表1的结果说明：在小样本的精致试验中,GRNN识别准确率可以达到理想的100%,效果最好。RBF和RBFE的识别率非常低,仅33%,无法有效识别,不可应用。PNN正确率67%介于它们之间。这对于研究工作来说有一定启示,我们一定可以通过改善训练集来提高RBF、RBFE、PNN的识别准确率。改善训练集有两个方向：一是增加样本数量,二是提高样本丰富程度。

2)试验2尝试改善训练集,方法是通过样本翻倍增大训练集,仿真的结果与表1完全相同。这说明前述单纯增加相同样本的数量无法提高准确率,训练集中“养分”有限,即便数量不翻倍也能被很好地“吸收”。改善训练集的两个方向之一被证明不可行。

3)试验3体现出了智能化方法的识别效果较为良好。PNN以外的三种网络虽然权值不直接取自训练样本,在仿真中不论对于训练样本还是轻微泛化的样本依然可以达到100%准确率,PNN没有准确识别出第三个样本,识别效果较差。试验2和3从实践中验证了,缩小训练集样本和测试集样本的差别可以有效提高准确率,在实际使用当中测试样本是未知的,因此，应当提高训练集样本的丰富程度和表达能力,同时增加训练集样本的数量,让训练样本尽可能地接近测试集。

4)如图所示,试验4中反人字队的测试样本与训练样本差别比较大,明显大于另外三种队形,此时GRNN网络能够达到100%准确率,RBF和RBFE准确率低至25%,PNN网络前两个样本识别准确,后两个样本识别错误。将表4与表1进行对比可知:RBF和RBFE并没有得到充分训练,识别不准确,总是将测试样本识别成最后一个训练样本,因此他们的识别有可能是随机的结果,这需要深入研究这两种网络的输出算法,在本文小样本的试验条件下这两种网络是不可选用的。经过本文的试验,我们推荐在小样本的情况下使用GRNN网络进行队形识别。PNN网络仅对于与训练样本差别较小的测试样本能够正确识别,在训练集较大的情况下可以使用。

存在的问题和进一步的工作:

1)本文中的试验基于小样本进行,每种队形仅3个训练样本,这仅能用于测试识别方法的性能和泛化能力,还应当准备更多样本,测试样本量充足的情况下智能化方法之间的差异和各自特点,论证本文的结论在样本充足时是否仍然成立,即当样本量变大时，4种神经网络的准确率是否呈现新的特点。

2)对比试验1和2,单纯使训练集翻倍对试验结果无影响。这仅仅是因为训练集中的重复样本无意义,还是因为训练样本少而容易被学习,在样本多的时候试验结果是否也呈现出这样的特点,这需要在样本充足的情况下进一步进行试验。

3)本文的试验中采用了一种巧妙的方法获取了传感器得到的位置信息,不经归一化直接提取出了样本特征,非常便于计算和数据的处理,但这种方法有局限性也不通用。随着潜艇中先进潜望设备的应用,我们可能需要直接处理数字化的图像,这些图像并非俯视而是自水平方向获取,仅能依靠图像中目标相对大小、相互阻挡情况、目标在图像中的位置等信息来进行队形识别,传统方法很难快速高效地完成,需要对卷积神经网络等深度学习方法进行应用论证和试验。