优化的BP神经网络在矢量水听器DOA估计的研究

白黄琴，胡红萍，白艳萍，王 鹏

（中北大学理学院，山西太原 030051）

0 引 言

在水声领域中，矢量水听器可测量声场中的矢量参数，它的应用有助于获得声场的矢量信息，其发展可以推动声纳系统的技术水平。在矢量水听器的研究中，波达方向也是重要研究方向之一。波达方向估计（Direction of Arrival Estimation，DOA）运用阵列信号处理的相关知识，确定同时处在空间某一区域内多个人们所感兴趣信号的空间位置。

针对来波到达角的估计问题，传统的高分辨率算法有很多种，如多重信号分类（Multiple Signal Classification，MUSIC）算法[1]、旋转不变子空间（Estimating Signal Parameters via Rotational Invariance Techniques，ESPRIT）算法[2]等。在某些情况下这些的确是一种解决问题的方法，但是大量的计算需要消耗很长的时间，对环境的要求很高，却不一定能达到实际的精度要求。然而神经网络因其非线性映射及泛化能力的特点，优点在于其建模过程采用训练样本来构造神经网络[3]，在实际情况下采集到的训练样本，可以将外界的环境、接收机噪声、信号模型、传输通道等因素考虑进去，而无需进行特征值分解以及谱峰搜索[4]，且计算使用时间也大大降低，从而有望应用到实际工程。

但是BP 神经网络对初始权值的选择非常敏感，由于参数选择不当，往往陷入局部极小，收敛速度慢。作为一种智能优化算法，灰狼优化算法具有全局搜索能力、收敛速度快、收敛精度高等特点，弥补了神经网络算法的不足[5]。本文提出差分进化算法和灰狼算法相结合的混合差分灰狼算法，用来优化BP 网络并对矢量水听器阵列信号进行DOA 估计。

1 本文采用的算法

1.1 灰狼算法

2014 年Seyedali Mirjalili[6]提出模拟灰狼狩猎机制的灰狼优化器（Grey Wolf Optimizer，GWO）。灰狼的社会等级分为α,β,δ,ω四个等级，其中，α是领导者，β帮助α做出决定，δ必须服从α和β，保护和保障团队的安全，ω扮演替罪羊的角色。灰狼猎杀的主要阶段有搜索猎物、包围猎物、猎捕、攻击猎物。

在GWO 中，创建一个随机的灰狼群X（候选解），根据α,β,δ的位置估计猎物Xp的可能位置，每个候选解更新其与猎物的距离。引入矢量A，当|A|＜1 时，候选解趋向于向猎物靠近，以进行下一阶段追赶，包围猎物。参数a分别从2 降到0，以强调勘探和开发。参数r1，r2是取值为[0，1]中的随机向量。

1）搜寻猎物

2）包围猎物

3）猎捕（假设α（最佳候选解），β和δ对猎物的潜在位置有更好的认识）

4) 攻击猎物

当A的值在[-1，1]中随机变化时，搜索代理的下一个位置是在它当前的位置和猎物的位置之间进行变化的。当|A|＜1 时，狼群做出攻击猎物的选择，找到了最优解。当|A|＞1 时，狼群往往会解散，远离猎物，从而失去了最佳的解决方案。

1.2 差分进化算法

差分进化（Differential Evolution，DE）算法是通过模拟生物进化机制提出的一种启发式群智能搜索算法[7]，存在类似于进化算法的计算步骤，包括变异、交叉和选择三种操作[8]。

设种群大小为N，xi=[xi1,xi2,…,xin],i=1,2,…,N为第i个个体，为种群个体的下界，为种群个体的上界，xp1，xp2，xp3为父代种群中随机选择的三个不同矢量，并且p1≠p2≠p3|≠i，rand(0,1)是[0,1]上服从均匀分布的随机数，F为[0，1]之间的缩放比例因子，CR 为取值在[0，1]之间的交叉概率。

1）初始化种群个体

2）变异操作

3）交叉操作

4）选择操作

1.3 差分灰狼算法

在GWO 中，群体根据α,β,δ的位置信息来更新自身位置，迅速向最优解集合[9]，从而使得算法优化精度高，收敛速度快，但容易致使整个狼群过早聚集于群体当前最优位置的某一邻域内，种群的多样性得不到有效保持，容易陷入局部最优；DE 算法采用DE/rand/1 的变异操作有利于保持种群的多样性，但搜索效率偏低[10]。因此，本文提出GWO 与DE 相结合的差分灰狼算法（DEGWO）。

DEGWO 算法的具体步骤如下：

1）参数初始化，N，tmax，D，ub，lb，CR，F，a，A和C。

2）对种群个体按式（9）实施DE 变异操作，得到中间体；然后按式（11）实施DE 选择操作，产生初始化种群个体，设置迭代次数t=1。

3）计算灰狼种群中每个个体的目标函数值，按照目标函数值的大小进行排序，选出最优的前三个个体分别记为Xα，Xβ和Xδ。

4）按式（5）计算种群中其他灰狼个体与最优的Xα，Xβ和Xδ的距离，并依据式（6）和式（7）更新当前每个灰狼个体的位置。

5）按式（1）和式（2）更新算法中a，A和C的值，按式（10）对种群个体的位置进行交叉操作，保留较优良的成分，然后执行式（11）进行选择操作产生新的个体，计算所有灰狼个体的目标函数值。

6）更新最优值前三的灰狼个体Xα，Xβ和Xδ的位置。

7）判定t是否达到tmax，若是，则算法结束，同时输出Xα的值和Xα的目标函数值；若不是，令t=t+1，转向步骤3）继续执行。

2 波达方向估计

2.1 矢量阵列信号的DOA 估计算法

矢量水听器阵列信号DOA 估计算法流程如图1所示。

图1 矢量水听器阵列信号DOA 估计算法流程Fig.1 Flow chart of DOA estimation algorithm for vector hydrophone array signal

2.2 仿真实验

2.2.1 两个信号源的DOA 估计

本文选用均匀的5 元天线阵列，信号源选用两个非相干的正弦信号，信噪比为10 dB，快拍数为1 000，阵元间距为半波长。信号源之间的间隔分别取12°和18°，从-90°～90°每隔0.5°取1 个样本，总共产生722 个样本，作为训练样本。信号源之间的间隔取15°，从-90°～90°每隔1°取一个样本，共产生181 个样本，作为测试样本。以间隔取12°为例，当第一个信号源为-90°时，第二个信号源为-78°；第一个信号源为-89.5°时，第二个信号源为-77.5°，按照这种间隔方式，覆盖整个[-90°，90°]的范围，进行200 次Monte-Carlo 仿真实验。

本文分别利用BP 神经网络，GWO-BP 网络，DEGWO-BP 网络对两信号源的DOA 方向进行估计，得到两信号的DOA 估计时输出预测曲线和估计误差曲线图，分别如图2～图5 所示。

图2 和图3 分别是第1 个信号和第2 个信号在3 种模型下的DOA 估计值和实际值。通过图2，图3 可以看出：用DEGWO-BP 网络算法的预测值更接近实际值，而BP 神经网络的预测值与实际值的差距最大，并且还有信息突变，误差较大，而GWO-BP 网络的算法预测值与实际值情况居中。图4和图5分别是第1个信号和第2个信号在3种模型下DOA 估计的误差曲线。从图4，图5 可以看出：DEGWO-BP 网络估计DOA 的误差曲线基本上都在另外两种算法的误差曲线范围之内，所以利用DEGWO-BP 网络算法得到的误差最小，而BP 神经网络估计DOA 得到的误差最大。通过DOA 输出曲线和误差曲线可以看出，本文提出DEGWO-BP 方法用于DOA 估计有更高的精度。

图2 信号1 的输出预测曲线Fig.2 Curve of output prediction of signal 1

图3 信号2 的输出预测曲线Fig.3 Curve of output prediction of signal 2

图4 信号1 的估计误差曲线Fig.4 Curves of estimation error of signal 1

2.2.2 算法比较

在两个信号源DOA 估计的仿真条件基础上，选用平均绝对误差（Mean Absolute Error，MAE）、均方误差（Mean Square Error，MSE）和均方根误差（Root Mean Square Error，RMSE）作为衡量算法的指标，得到表1，其中MAE1，MAE2 分别为第1 个信源和第2 个信源的指标。从表中两个信号各个指标的反馈，得到DEGWO-BP算法和GWO-BP 算法不仅对BP 网络用于DOA 估计有优势，对于文献[11-12]中所提的PSO-BP 和SAPSO-BP算法更是达到了优化的效果。所以本文提出的DEGWO-BP 算法用于DOA 估计具有一定的优势。

图5 信号2 的估计误差曲线Fig.5 Curves of estimation error of signal 2

表1 五种算法的DOA 估计误差统计Table 1 Error statistics for DOA estimation of five algorithms

2.2.3 不同信噪比下的RMSE

仿真条件与上文相同，利用DEGWO-BP算法，GWOBP 算法，BP 算法依次估计在信噪比为-10 dB，-5 dB，0 dB，5 dB，10 dB，15 dB 的RMSE，并且与PSO-BP 算法和SAPSO-BP 算法的RMSE 进行比较。结果如表2 所示，表2 中的RMSE 为两个信号源RMSE 的均值。

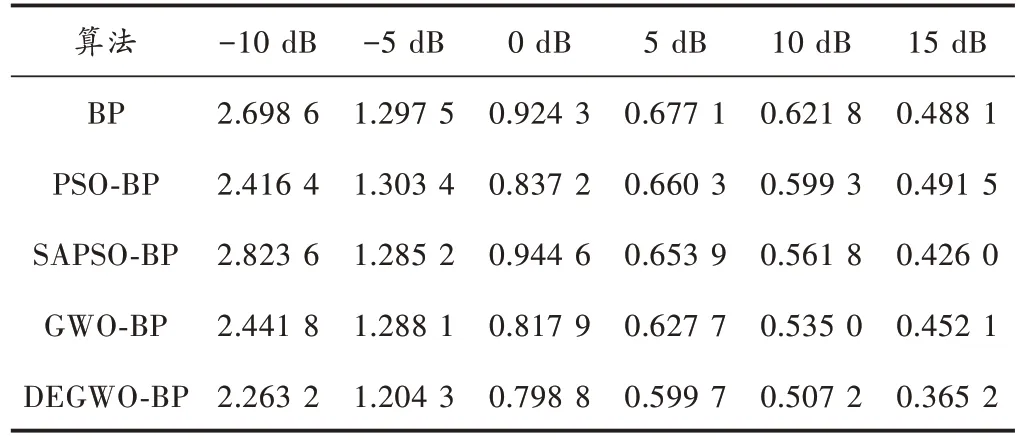
表2 五种算法在不同的信噪比下的RMSETable 2 RMSE of five algorithms at different SNR

从表2 的仿真结果可以看出：随着信噪比的不断增大，信源的RMSE 不断减小，而且在低信噪比的情况下，GWO-BP 算法和DEGWO-BP 算法的均方误差不仅比BP 网络的效果要好，而且比PSO-BP 算法和SAPSOBP 算法好，并且要更加稳定，还达到了优化效果。所以本文提出的算法具有更好的估计精度，且算法运行的时间很快，具有更好的应用前景。

3 结 语

本文提出差分进化算法与灰狼算法相结合的差分灰狼算法（DEGWO）优化BP 神经网络，用于实现矢量水听器阵列信号的波达方向估计以及在不同信噪比下的误差估计。仿真实验结果表明，DEGWO-BP 网络优于BP，GWO-BP，PSO-BP 和SAPSO-BP 网络，不仅有更好的估计精度，更好的收敛速度和优化性能，而且具有更好的普遍适用性以及良好的应用前景。