考虑断点续传的中继卫星调度模型及启发式算法
李夏苗,陈新江,伍国华,*,贺川,龙运军
1.中南大学 交通运输工程学院,长沙 410075 2.北京空间信息中继传输技术研究中心,北京 100094
跟踪与数据中继卫星(Tracking and Data Relay Satellite, TDRS),简称为中继卫星,主要为中、低轨道的航天器提供数据中继、连续跟踪与轨道测控服务[1]。中继卫星具有轨道高、覆盖面积大的特点,可以扩大中低轨道卫星与地面站之间的可见时间窗[1-3]。中继卫星系统作为同步地球静止轨道的天基传输平台,不仅需要执行预定任务,而且还为全球突发的应急任务服务,这对中继卫星任务的有效调度造成巨大的挑战[4]。
目前,国内外关于中继卫星的研究主要集中在中继卫星与用户航天器之间、不同的中继卫星之间的通信链路分析,包括天线的捕获跟踪与伪随机码的捕获[5-6],针对中继卫星任务调度的研究相对偏少。关于中继卫星任务规划问题的研究大多将其描述为带时间窗口的并行机调度问题(Parallel Machine Scheduling Problem with Time Windows, PMSPTW)[4, 7],其中中继卫星天线等同于机器,用户提交的任务等同于待加工的工件,并假设每个任务仅能被一颗中继卫星的一条天线执行,不允许断点续传,即不允许任务拆分。针对多中继卫星多用户航天器大规模任务申请的中继卫星调度场景,研究人员提出了多种模型和算法来解决中继卫星系统任务规划问题。调度模型包括混合整数优化模型[4, 7]、约束满足模型[8]和天线校准时间变长的规划优化模型[9]等。求解算法包括精确算法[4, 7]、启发式算法[10-15]和智能优化算法[8, 16-18]。
在精确算法上,Rojanasoonthon等[7]研究了任务具有两个时间窗口约束的中继卫星多址链路调度问题,采用分支-定界法对模型进行了求解。算法在求解小规模任务时能在较短时间内取得最优解,但求解大规模任务时很难在有效或合理时间内取得最优解。
在启发式算法上,基于规则的启发式算法是现有中继卫星调度系统中应用较多的算法。He等[10]构建了一个随机优化框架,将中继卫星多址天线动态混合任务调度问题等价地转换为一个内嵌多个天线时间分配问题的调度周期调整问题,并提出了求解问题的两种有效算法。Wang等[11]在考虑可见窗口和动态设置时间约束的基础上,建立了异构星间链路天线指向路径问题的数学模型,提出了一种基于分层调度策略的两阶段启发式求解算法。Liu等[12]构建了一个天线回转时间感知调度方案,将中继卫星任务调度问题转化为混合整数非线性规划问题,设计了一个多项式时间算法求解,实验结果表明,该方案显著提高了预定任务的完成率。Lin等[13]利用作业空闲时间窗的时域灵活性和统计特性,提出了一种启发式算法,与传统算法相比,该算法将任务的完成率提高约11%。
贺川等[14]在对按需申请模式下的中继卫星任务调度研究的基础上,构建了冲突任务检测和损失机会评估模型,并提出了基于冲突风险规避的任务规划算法,但文中并没有进行相关仿真实验。刘润滋等[15]通过设定一个任务拆分阈值,将服务时长大于该阈值的任务拆分成两个服务时长相等的子任务,并设计了一种多项式时间的启发式算法。通过实验验证了其在资源利用率等方面的增益。但任务拆分阈值的取值对调度效果的影响较大,且文中仅讨论了将任务拆分成两个服务时长相等的子任务。
在智能优化算法上,近年来,以蚁群算法(Ant Colony Algorithm, ACA)[16]、遗传算法(Genetic Algorithm, GA)[8, 17]、人工蜂群(Artificial Bee Colony, ABC)算法[18]、模拟退火(Simulated Annealing, SA)[16]为代表的智能优化算法在求解组合优化问题方面显示了较强的能力,在中继卫星调度问题中也得到了一定的应用。比如,顾中舜[16]利用蚁群算法求解中继卫星调度模型,并与基于遗传算法和模拟退火算法进行比较,结果表明,蚁群算法在求解时间和精度上都明显优于另外两种算法。
基于现有研究文献的分析,智能优化算法只适用于中、小规模的中继卫星调度场景的求解,针对多中继卫星多用户航天器大规模任务申请的中继卫星调度场景,会出现“维数灾”现象,导致智能优化算法性能迅速下降,求解时间也将大大超出实际调度工作要求。
根据当前的研究现状,可以发现:
1) 有部分文献研究了中继卫星任务调度问题,但是考虑断点续传的中继卫星调度模型和算法的相关研究依然缺乏。
2) 随着天基传输需求的日益增长,用户需求呈多样化增长[19-20],中继系统任务的规划也面临新的挑战,考虑断点续传的中继卫星应用模式在提高中继卫星系统效能与中继数传任务完成率等方面具有重要的研究意义。
本文在分析研究考虑断点续传的中继卫星系统任务规划问题的基础上,建立系统模型及设计求解算法,具体贡献与创新总结如下:
1) 考虑了在中继卫星任务调度周期内进行断点续传。为最大程度体现任务调度的灵活性,本文改进了传统的中继卫星应用模式,创新性地提出了考虑断点续传的中继卫星应用模式,将中继卫星任务调度过程划分为完整任务分配和断点续传任务分配阶段。同时提出了基于冲突风险评估的冲突度计算方法,将冲突度量化为一定时段内任务在其当前可见时间窗内发生冲突的概率。
2) 提出一种考虑断点续传的任务拆分方法,将原任务集合转化为子任务集合。以最大化任务完成率为目标函数,以任务需求、资源使用等约束为约束条件,构建了考虑断点续传的中继卫星任务规划模型。同时针对问题及模型特点设计了考虑断点续传的两阶段调度算法(Two-stage Scheduling algorithm Considering Breakpoint Transmission, TSCBT),算法第1阶段为完整任务分配阶段,采用基于最小冲突度的资源选择策略生成较优的初始可行调度方案;算法第2阶段为断点续传任务分配阶段,对完整任务分配阶段中未能成功调度的任务进行断点续传,采用基于最小任务拆分次数的资源选择策略生成最终调度方案。
3) 通过构建一个多中继卫星多用户航天器大规模任务申请的应用场景验证算法的有效性。同时通过实验将本文提出的算法与不考虑断点续传的贪婪算法(Greedy Algorithm)、基于最小冲突度的启发式算法(Heuristic Algorithm Based on Minimum Conflict Degree, HA-MCD)和基于任务优先级的启发式算法(Heuristic Algorithm based on Task Priority, HA-TP)比较,结果表明,本文提出的算法能分别将任务完成率提高7.67%、6.34%和8.67%。最后对算法进行性能测试与参数分析,验证了其在任务完成率和天线利用率等方面的增益。
1 中继卫星任务规划问题及模型
1.1 问题描述与模型假设
中继卫星任务规划过程如图1所示,中继业务系统由3层网络组成:位于高轨道的骨干网络层、中低轨道的用户层和地面网络层,各层网络具体组成部分和功能为:由数据中继卫星(Data Relay Satellite, DRS)组成的骨干网络负责向用户层提供数据中继服务。用户层主要包括各种卫星、近空飞行器以及深空探测器。地面网络层包括网络化地面终端(networked Ground Terminal, GT)、用户管理中心(User Manage Center, UMC)和数据中继网络管理中心(Manage Center of data relay satellite networks, MC)。通常,任务请求通过地面网络从UMC提交到MC。

图1 中继卫星系统任务规划过程Fig.1 Relay satellite system mission planning process
中继卫星天线任务调度是指在满足任务需求约束和资源使用约束的前提下,在合理的时间内得到一种最优的调度方案[21]。其调度难点主要有以下两点:① 中继卫星调度问题是NP-hard问题,求解难度大;② 问题规模大,加上其复杂性和多约束的特点而难于求解。中继卫星与用户航天器之间并非时时可见,二者在不同的时段有不同的可见时间窗口。常将中继卫星调度问题描述为带时间窗的并行机调度问题,其约束主要包括任务服务时长、任务服务时间窗口、可见时间窗口、天线使用约束等[22-23]。
1.2 中继卫星系统基本要素

任务需求的基本要素可用一个六元组{pt,startt,endt,ntimet,Rt,ust}表示。其中pi表示任务的优先级或权重,任务优先级是描述任务重要程度的唯一标识码,是决定任务调度顺序的主要参考标准。[startt,endt]表示任务的服务时间窗口,用户依据中继卫星相关管理机构发布的可用中继卫星资源,结合自身需求提出任务在某段可见时间窗内完成的要求。startt表示任务允许服务的最早开始时刻;endt表示任务允许服务的最晚结束时刻;ntimet表示任务t期望服务时长,即完成任务t所需的时间;Rt表示任务t可用天线集合;ust表示任务所属用户航天器。


图2 任务的时效性特征Fig.2 Time efficiency of task
根据上述分析,中继卫星任务调度可以描述为:制定调度方案P,在满足天线使用要求的前提下(同一时刻同一天线仅能服务一个任务),使得任务能够在[startt,endt]内被Rt中一副或多副天线服务,且任务总服务时长等于ntimet。
1.3 中继卫星应用模式设定
假设图3为中继卫星的一个应用场景,传统的中继卫星应用模式包括用户申请方式、资源释放方式、申请处理方式、计划调整权限等相关要求和规则[24-25]。上述中继卫星应用模式可以归纳为:① 用户基于任务需求申请一个确定的时间窗口,每项任务对应一个时间窗口;② 中继卫星资源(主要是可见时间窗口资源)周期性释放;③ 调度工作根据任务申请信息和周期性释放的中继卫星资源进行调度方案安排。
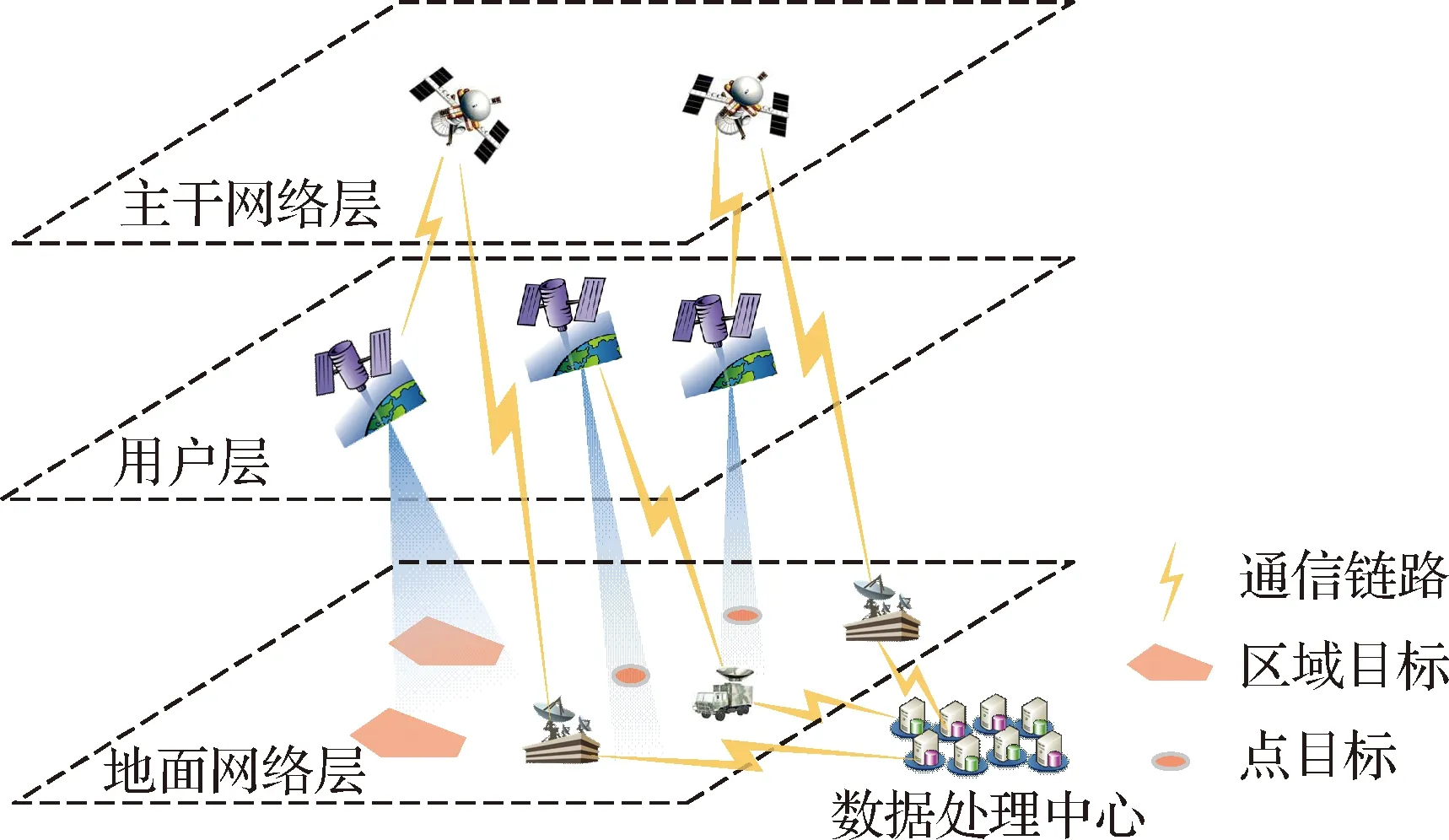
图3 中继卫星应用场景Fig.3 Relay satellite scheduling scenario
上述应用模式主要存在以下问题:① 由于每项任务只允许申请一个时间窗口,且不允许任务进行断点续传,如果在调度过程中无法满足该时间窗口,则该任务将无法成功调度;② 难以通过合理调度实现不同任务间的冲突消解,不利于提高调度工作的灵活性和调度方案质量。
基于以上分析,为更好地适应用户需求特点和工作实际,提出考虑断点续传的中继卫星应用模式:中继卫星任务调度主要分两个阶段进行,第1阶段为完整任务分配阶段,在此阶段中,中继卫星优先对不需进行断点续传的任务进行调度;第2阶段为断点续传任务分配阶段,在此阶段中,将第1阶段中未能成功调度的任务采用断点续传的方式进行调度。
1.4 优化模型
任务拆分在调度过程中动态进行,具体方法在2.2节介绍。假设任务经过拆分后的子任务集合为{t1,t2,…,tn},ntimetn表示任务第n个子任务的期望服务时长,子任务服务时长满足:
(1)
用Tα表示T中拆分成功的任务集,T1表示Tα中任务拆分后子任务集合,则有
T1={tn|tn∈{t1,t2,…,tn}=ZC(t),t∈Tα}
(2)
式中:ZC(t)表示原任务与子任务之间的转化关系[15],即tn∈{t1,t2,…,tn}=ZC(t)可抽象表示为将任务拆分成n个子任务。
用Tβ表示T中不需进行拆分的任务集,即
T=Tα∩Tβ
(3)
将Tβ转化为子任务集T2,即
T2=Tβ
(4)
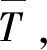
(5)
1) 优化目标
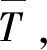

(6)
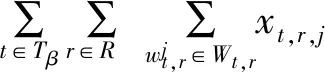
xt2,r,j,…,xtn,r,j)=1
(7)
2) 任务需求约束

(8)
(9)
tstartt,r,j≥starttxt,r,j
(10)
(tstartt,r,j+stimet,r,j)xt,r,j≤endt
(11)
(12)
(13)
其中:式(8)和式(9)表示任务服务时长约束;原任务或子任务的实际服务时长等于其期望服务时长;式(10)表示服务时间窗口约束;原任务或子任务的实际执行时刻不早于其允许的最早开始时刻;式(11)表示原任务或子任务的实际结束时刻不晚于其允许的最晚结束时刻;式(12)表示每个原任务或子任务只选择一条天线服务;式(13)表示每个原任务或子任务只在一个可见时间窗口内调度。
3) 资源使用约束
定义Et,r为任务t在天线r中实际执行的时间段。中继卫星任务规划过程中的资源使用约束主要包括任务与天线可见时间窗口和中继卫星天线使用约束:① 中继卫星与用户航天器的可见时间窗口的起始时刻由二者的轨道参数共同决定,任务的调度时段应落在用户航天器与中继卫星天线的可见时间窗口内;② 同一时刻同一中继卫星天线仅能执行一项任务。即
(14)
(15)
(adjust+Em,r+rec)∧(adjust+En,r+rec)=∅
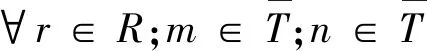
(16)
其中:式(14)和式(15)为任务与天线的可见时间窗约束,式(14)表示原任务或子任务的实际开始时刻不早于其可见时间窗的开始时刻,式(15)表示原任务或子任务的实际结束不晚于其可见时间窗的结束时刻;式(16)表示同一时刻同一中继卫星天线仅能执行一项任务。
综上所述,以最大化任务完成率为目标函数,以任务使用约束和资源使用约束为约束条件构建了考虑断点续传的中继卫星任务规划模型式(6)~式(16)。可知优化模型属于高维混合整数优化问题,具有组合优化问题的特征,其解空间随着资源与任务数量的增长将呈指数增长[24-25]。此外,模型还涉及复杂的约束条件,采用常见的智能优化算法求解将面临搜索和寻优困难。较高的决策变量维度以及复杂的约束条件使得本模型的求解难度较大[27-28]。一般的通用算法难以直接用于求解本模型。因此,针对问题和模型特点设计了考虑断点续传的两阶段调度算法。
2 考虑断点续传的两阶段调度算法
关于中继卫星任务规划的研究大多将其描述为带时间窗约束的并行机调度问题,并假设任务不可拆分。这种假设没有充分考虑中继卫星业务的实际情况和部分任务的特殊需求,造成中继卫星资源浪费和服务时长较长的任务完成率低等问题。实际上,中继业务系统支持对较大的数据进行拆分分组,不同的分组可在不同的时间采用不同的路径回传[29],即本文所考虑的断点续传。
在中继卫星任务规划过程中应用断点续传机制的必要性和优越性有:① 能够有效减少中继卫星系统待机空转时间,提高中继卫星系统应用效能。若不允许拆分任务,则会增加中继卫星在其可用时段内的闲置待机时间,造成资源浪费和降低中继系统效能。② 断点续传机制适应中继卫星业务的实际需求,能有效提高任务完成率。调度服务时长较长的任务需消耗更多的资源,即此类任务与其他任务发生冲突的可能性也就越大,导致任务调度成功率低等问题。而这一问题主要是由上述假设任务不可拆分导致的。采用断点续传机制可以有效解决该问题,提高服务时长较长的任务完成率。
假设任务i、任务j和任务k的期望服务时长及其与天线的可见时间窗口如图4(a)所示,在以往假定任务每个任务仅能被一颗中继卫星的一条天线执行,不允许断点续传的前提下,任务i、任务j和任务k无法同时调度成功。
显然,采用断点续传的调度方式可以提高服务时间较长的任务的调度成功率,如图4(b)所示。其中stimekn,r,j({k1,k2,…,kn}=ZC(k))表示任务k拆分后的第n个子任务与天线r的第j个可见时间窗口内的实际服务时间。图4(b)中将任务k拆分成子任务k1、k2后,可在不同时段内调度完成。
考虑断点续传的两阶段调度算法主要包括以下6个算法模块:① 任务资源匹配;② 任务拆分;③ 生成任务可用资源集;④ 计算可用时段冲突度;⑤ 任务插空;⑥ 任务可用资源集更新。
模块①是根据任务提交的服务时间窗口及任务的服务时长,为任务匹配当前可用的时段资源。模块②是根据当前任务的资源匹配结果,判断任务是否需要进行拆分,若没有满足任务的服务时长需求的可用资源,则将原任务拆分成若干个子任务。需要注意的是,任务拆分操作是在调度过程中实时动态地进行。模块③是根据模块①的匹配结果和模块②的拆分结果,生成当前任务的可用资源集合。模块④是根据任务可用资源集,计算每个任务可用时段的冲突度。冲突度是评价在同一中继卫星天线下任务可用资源被其他任务的可用时段侵占程度。因此,为了提高资源的利用率和任务完成率,优先选择最小冲突度的可用时段作为任务的执行时段。模块⑤是选定任务的执行时段后,进行任务插空,常见的任务插空策略有紧前策略、紧后策略、随机策略。模块⑥是任务调度成功后,刷新任务集和任务可用资源集。
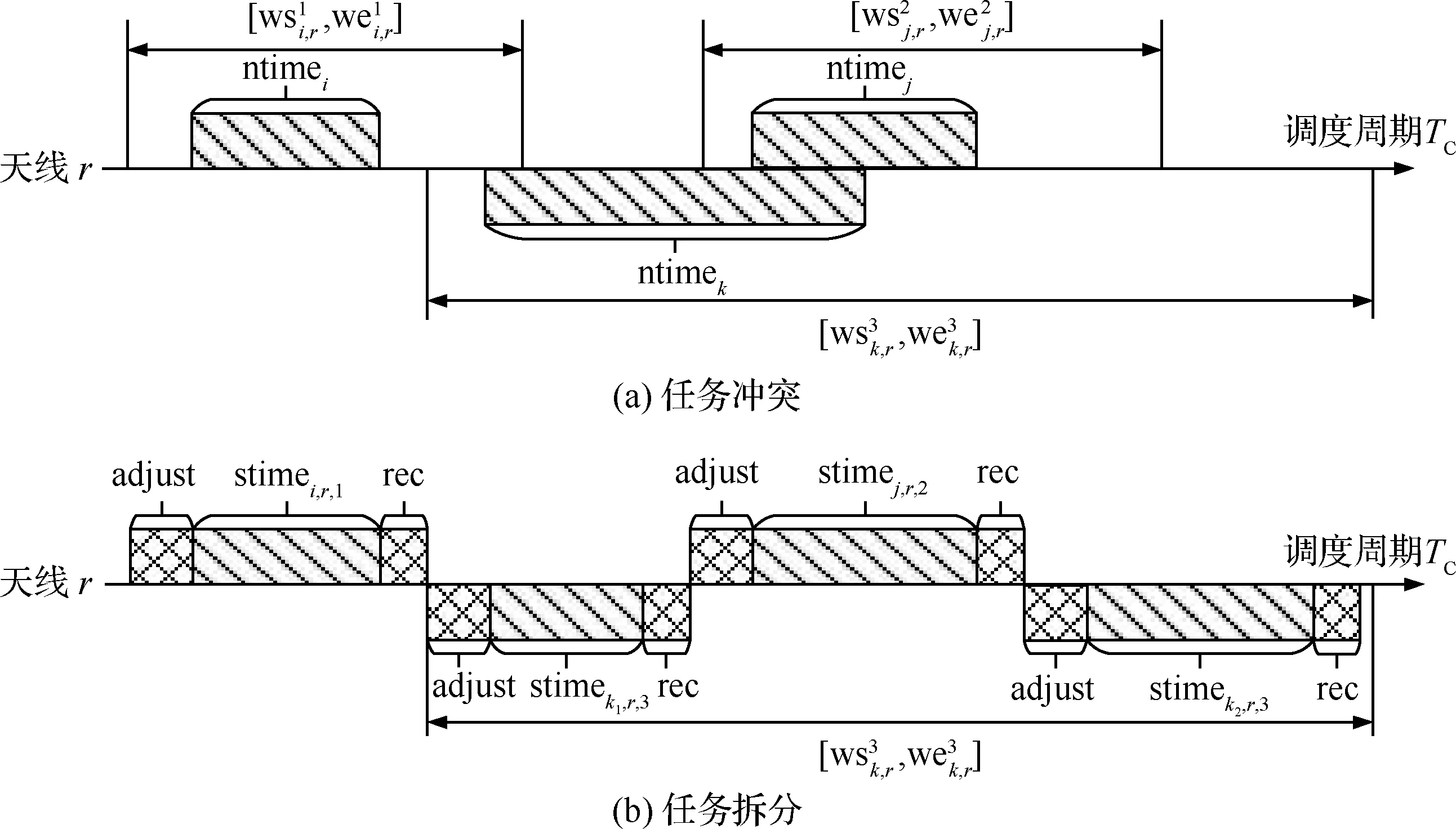
图4 断点续传示意图Fig.4 Diagram of breakpoint transmission
考虑断点续传的两阶段调度算法属于构造型算法,算法着重考虑任务需求的差异性和中继卫星资源的利用率,通过采用合理的解构造策略,生成较优的调度方案。在完整任务分配阶段,重点考察任务之间冲突度,对任务所有可用时段进行冲突度评价,根据评价结果选择任务的可用资源,采用基于最小冲突度的冲突规避策略生成较优的初始可行调度方案。在断点续传任务分配阶段,着重考虑中继卫星资源的利用率和用户的实际需求,对完整任务分配阶段中未能成功调度的任务进行断点续传。同时兼顾中继业务的实际情况:在中继卫星任务调度过程中,任务切换时天线会有一定的空转时间[30-31],任务切换次数增多,天线空转时间越多,势必会造成天线可用资源的损耗和浪费。故在此阶段采用基于最小任务拆分次数的资源选择策略,生成最终调度方案。
基于上述分析,设定任务进行断点续传的两个原则:① 任务拆分后的子任务优先在同一中继卫星进行调度;② 基于最小拆分次数进行子任务的资源匹配和任务插空。
2.1 任务资源匹配方法
任务资源匹配主要是将任务提交的服务时间窗口、服务时长与其可见时间窗口对比,匹配结果为生成当前任务可用的时段资源,并生成决策变量的约束信息。任务资源匹配具体方法如下。
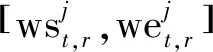
(17)
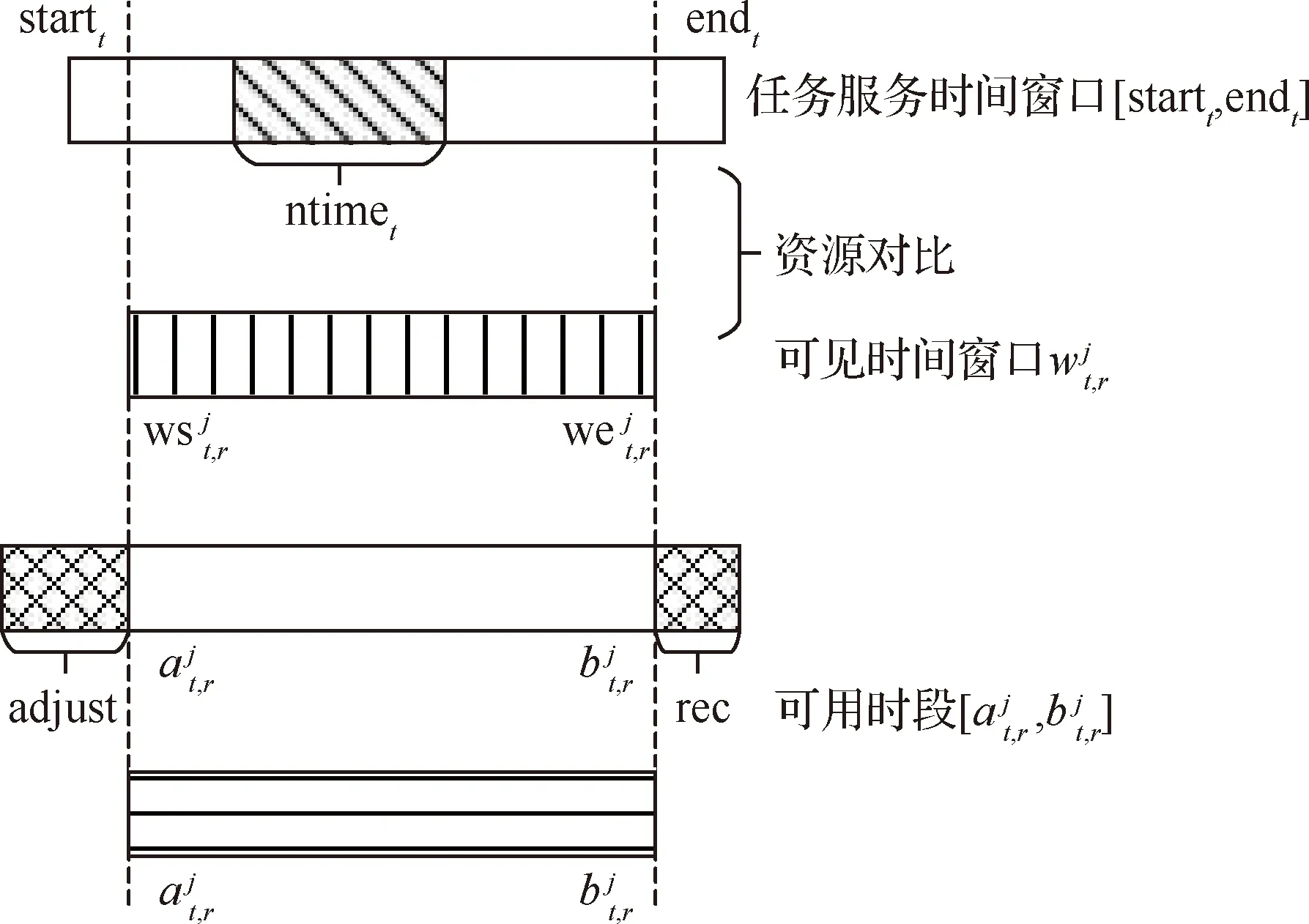
图5 任务资源匹配方法示意图Fig.5 Diagram of task resource matching method
2.2 任务拆分
针对调度过程中服务时间较长或优先级较低的任务在资源匹配阶段难以匹配到合适可用资源的问题,提出了一种考虑断点续传的任务拆分方法,该方法是在调度过程中对任务的动态处理。根据资源匹配结果,对于任务,若任务最长的可用时间窗口不满足其服务时长需求,即
(18)
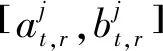
(19)
式中:ntimet1和ntimet2分别表示任务t的第1和第2个子任务的期望服务时长。任务t拆分后的子任务优先级、允许执行的最早开始时刻、最晚结束时刻、服务天线和所属用户航天器与原任务一致,子任务期望服务时长的累加和等于原任务的期望服务时长,即
ntimet1+ntimet2=ntimet
(20)
(21)
值得注意的是,当最长可见时间窗口不满足任务t1、t2的服务时长需求时,又可将t1、t2拆分成更细小的子任务,即t1、t2拆分后的子任务都可视为任务的子任务,令Tα=Tα∪{t},即
(22)
2.3 生成任务可用资源集
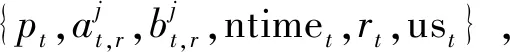
2.4 计算任务可用时段冲突度
不同任务可用时间窗口存在交叉重叠,由于任务执行时刻存在不确定性,即可视为任务服务时段可在其可用时间窗内滑动,同时受天线使用约束(同一天线同一时刻仅能执行一项任务)限制,不同任务在同一天线下的可用时间窗口可能存在冲突,如图6所示。

图6 任务可用时段冲突示意图Fig.6 Diagram of conflict at avaliable task time
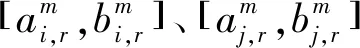

图7 冲突度计算方法示意图Fig.7 Conflict degree calculation method
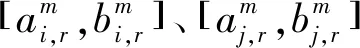
tstartj,r,n-tstarti,r,m>adjust+ntimei
(23)
tstarti,r,m-tstartj,r,n>adjust+ntimej
(24)
则任务i、j在当前可用时间窗内不冲突。当满足以下任一条件时:
tstartj,r,n-tstarti,r,m (25) tstarti,r,m-tstartj,r,n (26) (27) 式中:pi为任务i的优先级或权重。在任务调度过程中,为了提高任务调度的成功率和减小对其他任务调度的干扰和资源损耗,总是优先选择冲突度最小的可用时段作为当前任务的执行时段。 图8 任务插空策略Fig.8 Task insertion strategy 任务调度成功后,会占用任务与天线的可见时间窗口,其他用户航天器与该中继卫星的天线的可见时段可能与任务占用时段存在交集。由于同一中继卫星同一时刻仅能执行一项任务,所以需要刷新可见时间窗口。假设调度过程中任务服务时间为(T3,T4),则可根据(T3,T4)对其他任务可见时间窗口的侵占情况刷新任务资源,将各类情况总结如表1所示。 表1 不同情况下资源刷新结果Table 1 Resource refresh results in different situations 基于上述分析,考虑断点续传的两阶段调度算法如算法1所示。 算法1考虑断点续传的两阶段调度算法1.初始化Tα=∅,TaskResource1=∅,TaskResource2=∅,i=1,T为任务集,P为调度方案2.将任务按照任务优先级排序,生成任务集T=1,2,…,i,…,n{}3.完整任务分配阶段4.foreachi∈T5.进行任务资源匹配,生成任务可用资源集TaskResource1=pi,aji,r,bji,r,ntimei,ri,usi{}6.计算所有可用时段aji,r,bji,r[]冲突度cji,r7.按cji,r数值由小到大的顺序遍历aji,r,bji,r[]8.if∃bji,r-aji,r()≥ntimeii∈T()9.任务调度成功,更新TaskResource1、P10.elseif∀bji,r-aji,r() 观察上述算法流程可知,完整任务分配阶段(第4~13行)算法复杂度为O(nW+nRa),其中n为任务数,W为可见时间窗口数量,Ra为可用时间窗口数量,由于W>Ra,所以完整任务分配阶段(第4~13行)算法时间复杂度为O(nW)。同理,断点续传任务分配阶段(第15~25行)算法时间复杂度为O(|Tα|W),其中,|Tα|为需进行断点续传的任务数量。由于|Tα|≤n,即O(|Tα|W)≤O(nW)。故所提算法的时间复杂度为O(nW),所提算法可在多项式时间内执行完毕。 在任务需求仿真阶段,分别运用正态分布确定任务的期望服务时长及其服务时间窗口,即 (28) (29) startt=start+rand()×(end-start) (30) endt=startt+abs(normrnd(cmean,cstd)) (31) 假设在任务申请阶段中共收到300个任务,任务需求参数设置如表2所示。 表2 任务需求参数设置Table 2 Task requirement parameter setting 在仿真实验中构建了一个调度周期为1天,由3颗中继卫星、10个用户航天器的中继卫星应用场景,每颗中继卫星携带一副单址天线用于执行常规任务,天线对准时间为360 s,复位时间为240 s,应用场景参数设置如表3所示。 表3 应用场景参数设置Table 3 Application scenario parameter setting 实验平台为2.80 GHz Intel Core CPU、8 GB内存、Windows 10操作系统的PC机。由于考虑断点续传的中继卫星应用模式目前没有标准测试集可供调用,故首先运用STK与MATLAB软件进行资源与任务需求仿真,获取实验数据,再运用MATLAB R2016b对本文所提算法进行测试。 运用考虑断点续传的两阶段调度算法对上述实例进行测试,同时,在同一中继卫星调度场景下,将考虑断点续传的两阶段调度算法(TSCBT)与贪婪算法(Greedy Algorithm)、基于最小冲突度的启发式算法(HA-MCD)和基于任务优先级的启发式算法(HA-TP)比较。其中贪婪算法的贪婪策略为选取单位时间内权重(Wt=pt/ntimet)最大的任务,HA-MCD除了不考虑任务的断点续传,其他算法模块与TSCBT一致。HA-TP主要步骤如下: 步骤1将任务按照任务优先级排序,形成任务集T。 步骤2依次从任务集T中选取优先级最高的任务t。 步骤3遍历任务t的可用时段资源,为其安排可用资源,并将任务t从任务集T中删除。如果T=∅,算法结束;否则转步骤2。 实验结果如表4所示,结果表明,TSCBT仅用了0.218 84 s就完成了对300个任务的调度,任务完成率达到84.67%,算法整体性能较好。此外,TSCBT能显著将Greedy Algorithm、HA-MCD和HA-TP的任务完成率从分别从77.00%、78.33%和76.00%提高到84.67%,HA-MCD能分别将Greedy Algorithm和HA-TP的任务完成率从77.00%和76.00%提高到78.33%。这验证了采用断点续传机制对任务完成率的增益,同时也验证了基于最小冲突度的任务资源选择策略能够有效地实现冲突规避。 表4 不同算法运行结果Table 4 Running results of different algorithm 从TSCBT的求解结果中,选取10个任务的调度方案进行分析,如表5所示,其中调度时段为2019年5月15日0~24时,“+1”表示任务以完整任务分配方式调度(即任务不拆分),“+2”表示任务以断点续传分配方式调度。观察表5可知,不拆分方式调度的任务,任务从开始到完成的持续时间为单一的时间段。以断点续传方式调度的任务,由于任务被拆分成若干个子任务,子任务在多个可用时间段内完成,所以任务从开始到完成的持续时间由若干时间段组成。 表5 TSCBT部分调度方案Table 5 Partial scheduling plans of TSCBT 为了测试本文所提出算法的性能,同时对影响算法的参数进行分析,在3.2节构建的中继卫星调度应用场景中,依次分析不同任务规模、不同用户航天器数量、不同中继卫星数量和不同服务时长对算法的影响。分30组实验进行测试,各组实验具体参数设置如表6所示。最后分别运用TSCBT、Greedy Algorithm、HA-MCD和HA-TP算法对以上30组不同参数设置的调度场景进行测试。实验结果如图9~图14、表7~表9所示。 表6 实验参数设置Table 6 Experimental parameters setting 图9 不同任务规模下算法性能测试结果Fig.9 Algorithm performance test results for different number of tasks 图10 不同用户航天器数量下算法性能测试结果Fig.10 Algorithm performance test results for different number of spacecraft 图11 不同中继卫星数量下算法性能测试结果Fig.11 Algorithm performance test results for different number of TDRSs 图12 任务完成率提升程度对比Fig.12 Comparison of task completion rate 图13 天线利用率对比Fig.13 Comparison of antenna utilization ratios 实验结果表明,在求解中继卫星调度问题时,TSCBT算法总是优于Greedy Algorithm、HA-MCD和HA-TP算法,考虑断点续传的中继卫星应用模式对中继卫星任务完成率和资源利用率有明显的增益。算法评价指标和运行时间随用户航天器数量的波动呈现小幅度波动,可见用户航天器数量对算法性能和调度工作影响较小。 值得注意的是,4种算法的任务完成数和任务完成率均随任务规模和中继卫星数量的增大而增大,当到达一定程度之后,任务完成数和任务完成率增长速度明显减缓。前者是因为在当前算法性能下,中继卫星天线资源已接近其最大利用率,后者是因为任务可用资源已接近其最大利用率,任务完成率难以实现进一步增长[32-33]。同时,随着任务数量和中继卫星数量的增多,4种算法的任务完成数的增长速度远小于任务申请的增长速度,算法运行时间也随之增长,可见二者对调度工作和算法性能有较大影响。 观察图12~图14可知,相比于没有考虑断点续传的Greedy Algorithm、HA-MCD和HA-TP算法,TSCBT对服务时长较长的任务调度成功率有明显的增益,且其天线利用率也高于其他3种算法,波动较为平稳。 图14 不同调度方式完成任务占比Fig.14 Ratio of tasks completed for different scheduling modes 表7 不同任务规模下算法性能测试结果 实验编号任务完成数任务完成率/%算法运行时间/sTSCBTGreedyHA-MCDHA-TPTSCBTGreedyHA-MCDHA-TPTSCBTGreedyHA-MCDHA-TPC119218318618096.0091.5093.0090.000.099430.938120.103830.08472C225423123522884.6777.0078.3376.000.218840.212230.218690.20373C330824225223577.0060.5063.0058.750.468850.432730.457820.38753C431924424824063.8048.8049.6048.000.703740.684060.708750.54518C533524925624355.8341.5042.6740.501.236551.087461.153930.83385C633325025524747.5737.7136.4335.292.066361.785621.792951.26859C733825927125242.2532.3633.8831.503.004712.776253.306452.28433 表8 不同用户航天器数量下算法性能测试结果Table 8 Algorithm performance test results for different number of spacecraft 表9 不同中继卫星数量下算法性能测试结果Table 9 Algorithm performance test results for different number of TDRSs TSCBT能显著提高任务完成率的主要原因可从断点续传机制在任务规划和资源利用上的优越性来分析:① TSCBT在调度过程中应用了断点续传机制,即允许对任务进行合理拆分,使其在多个时间窗口内完成,这大大提高了任务成功调度的可能性;② 在资源利用方面,若不考虑断点续传,优先级较低或服务时长较长的任务通常面临着调度资源不足、可用资源不满足任务服务时长需求等难题,造成此类任务完成率低。而采用断点续传机制能充分利用中继卫星剩余可用资源,为任务规划提供更多可用资源,进一步提高任务成功调度的可能性。 在算法的调度开销上,可以从两方面进行讨论:① 理论上4种算法的时间复杂都为O(nW);② 仿真实验中4种算法的运行时间差距不大。实际上,TSCBT算法比Greedy Algorithm、HA-MCD和HA-TP算法增加了对断点续传任务的调度规划,而TSCBT不仅显著提高了预定任务的完成率,且运行时间与其他3种算法几乎一致,可见与传统中继卫星应用模式相比,采用断点续传机制能有效降低调度开销,提高任务完成率。 本文在分析任务拆分机制的基础上,构建了考虑断点续传的中继卫星单址天线调度模型和设计了考虑断点续传的两阶段调度算法,获得以下结论: 1) 考虑断点续传的中继卫星任务规划模型阐明了任务拆分机制,统一表征了原任务与子任务的内在联系,对创新和开发中继卫星系统应用模式具有一定的借鉴意义。 2) 基于冲突风险评估的冲突度量化方法提供了一种计算可滑动时间窗口冲突度大小的方法,根据其原理衍生的基于最小冲突度的冲突规避策略能分别将任务完成率提高1.33%和2.33%,有效地降低了资源损耗。 3) 考虑断点续传的两阶段调度算法采用基于最小冲突度和基于最小任务拆分次数的资源选择策略,能分别将任务完成率提高7.67%、6.34%和8.67%,将天线利用率提高2.00%以上,显著提升了中继系统应用效能。
2.5 任务插空策略

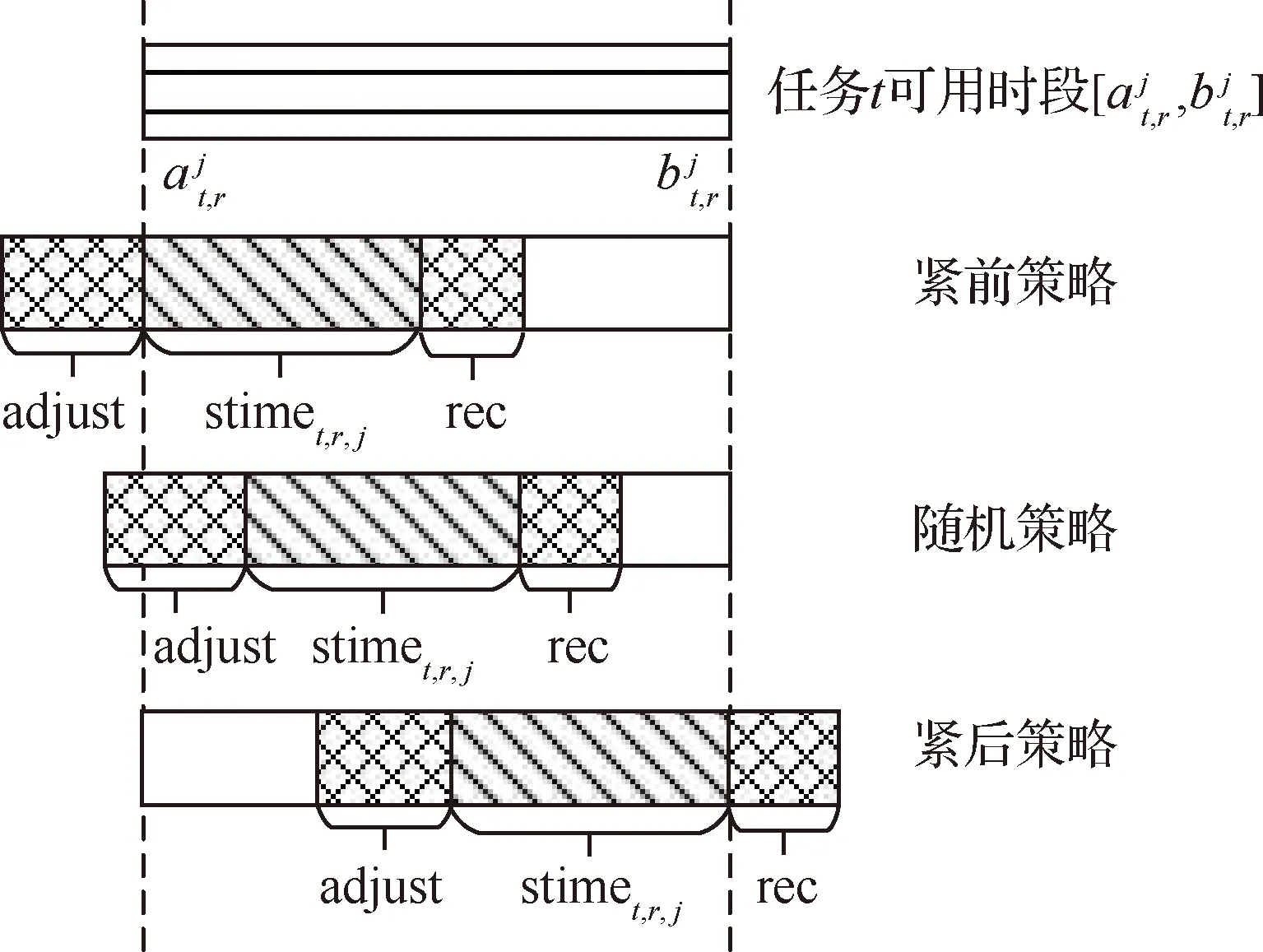
2.6 任务可用资源集更新

2.7 算法框架与流程

3 仿真实验
3.1 任务需求仿真
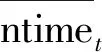
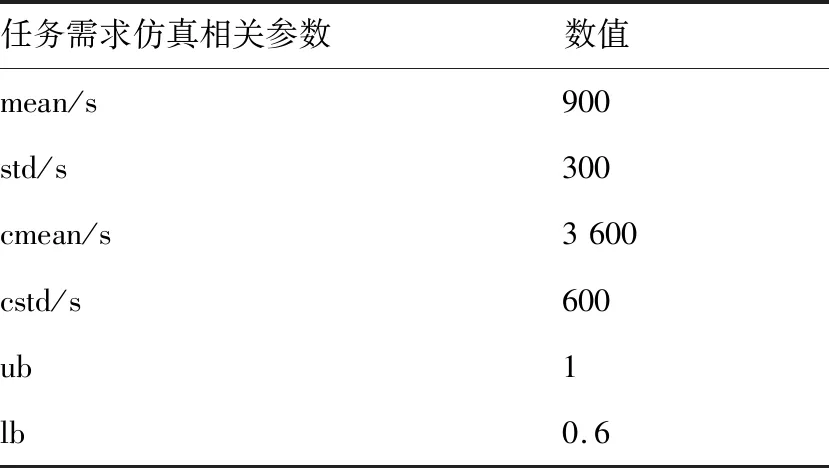
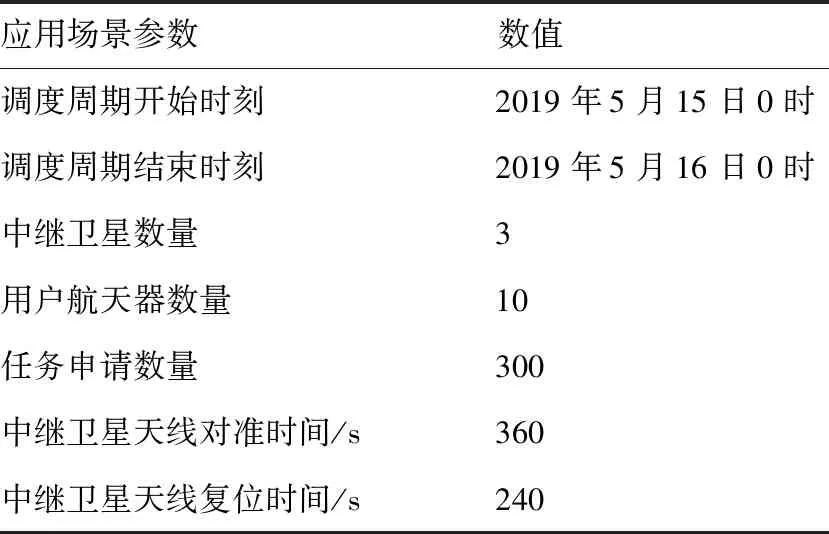
3.2 仿真场景参数设置
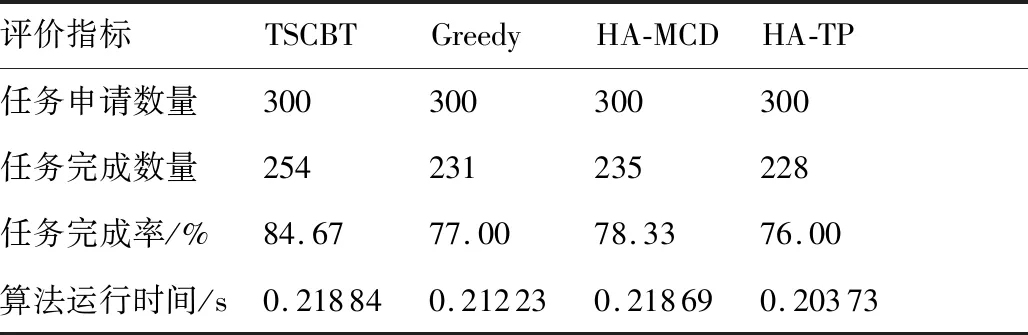
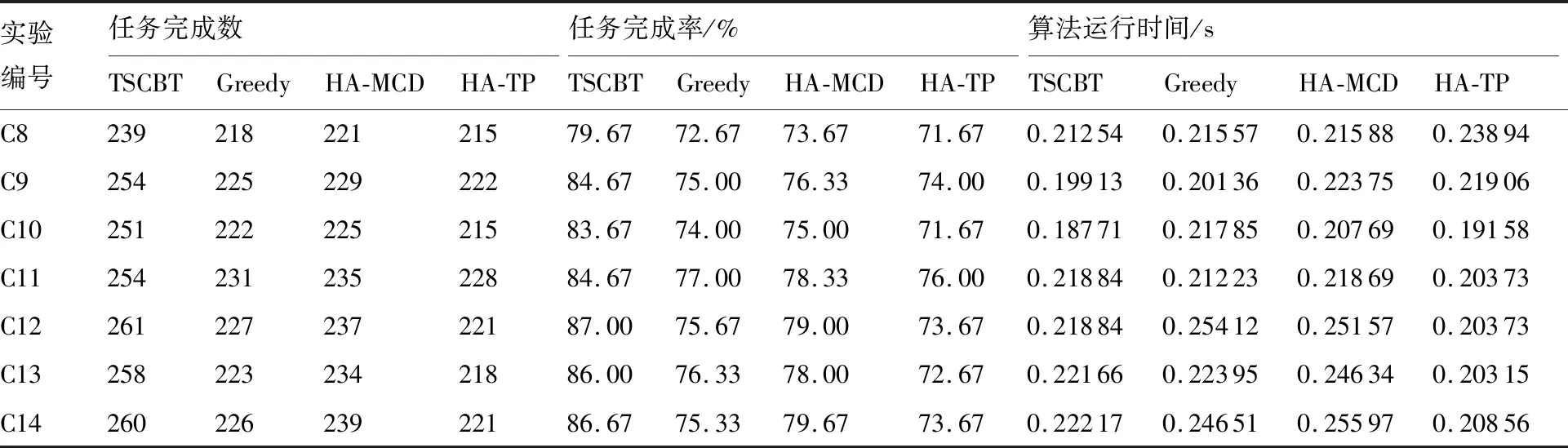
3.3 实验结果
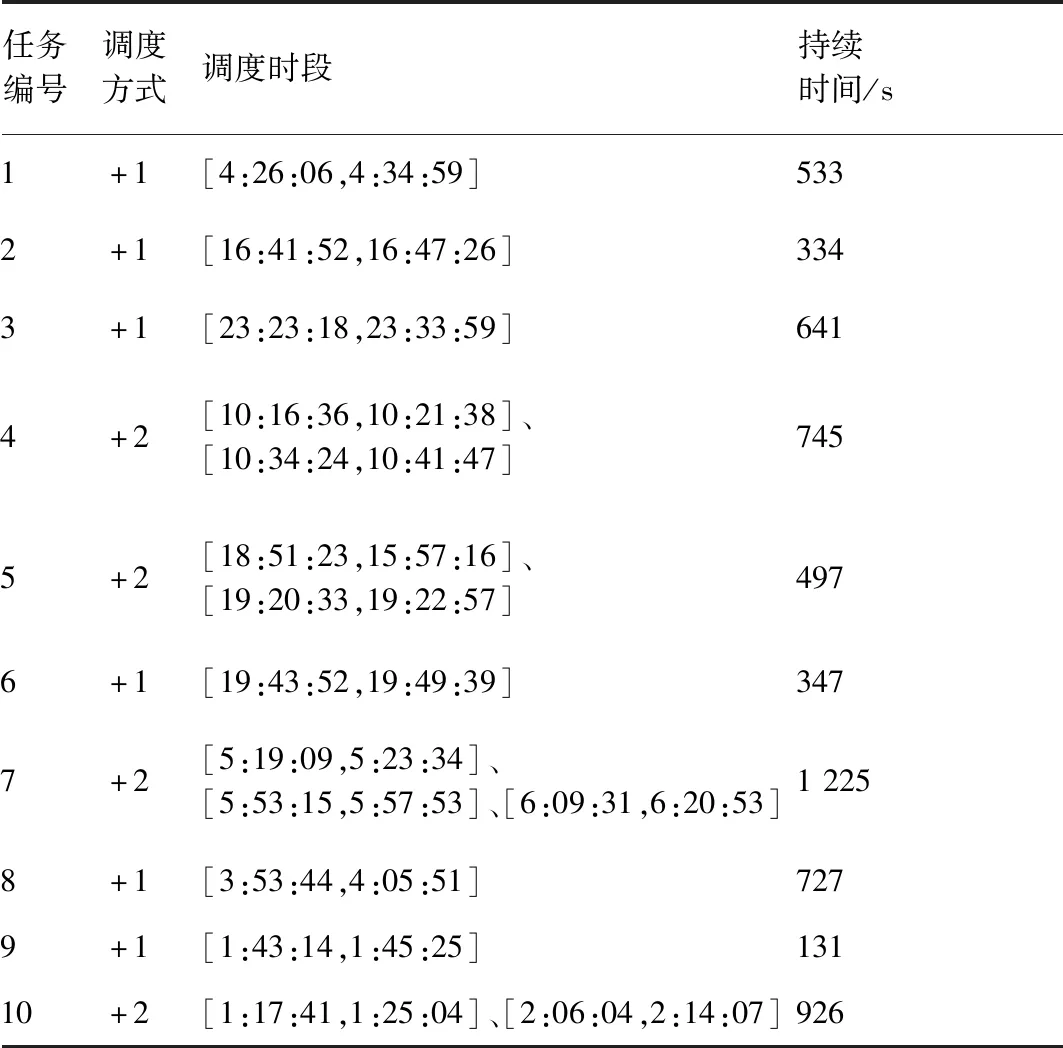
3.4 算法性能测试与参数分析
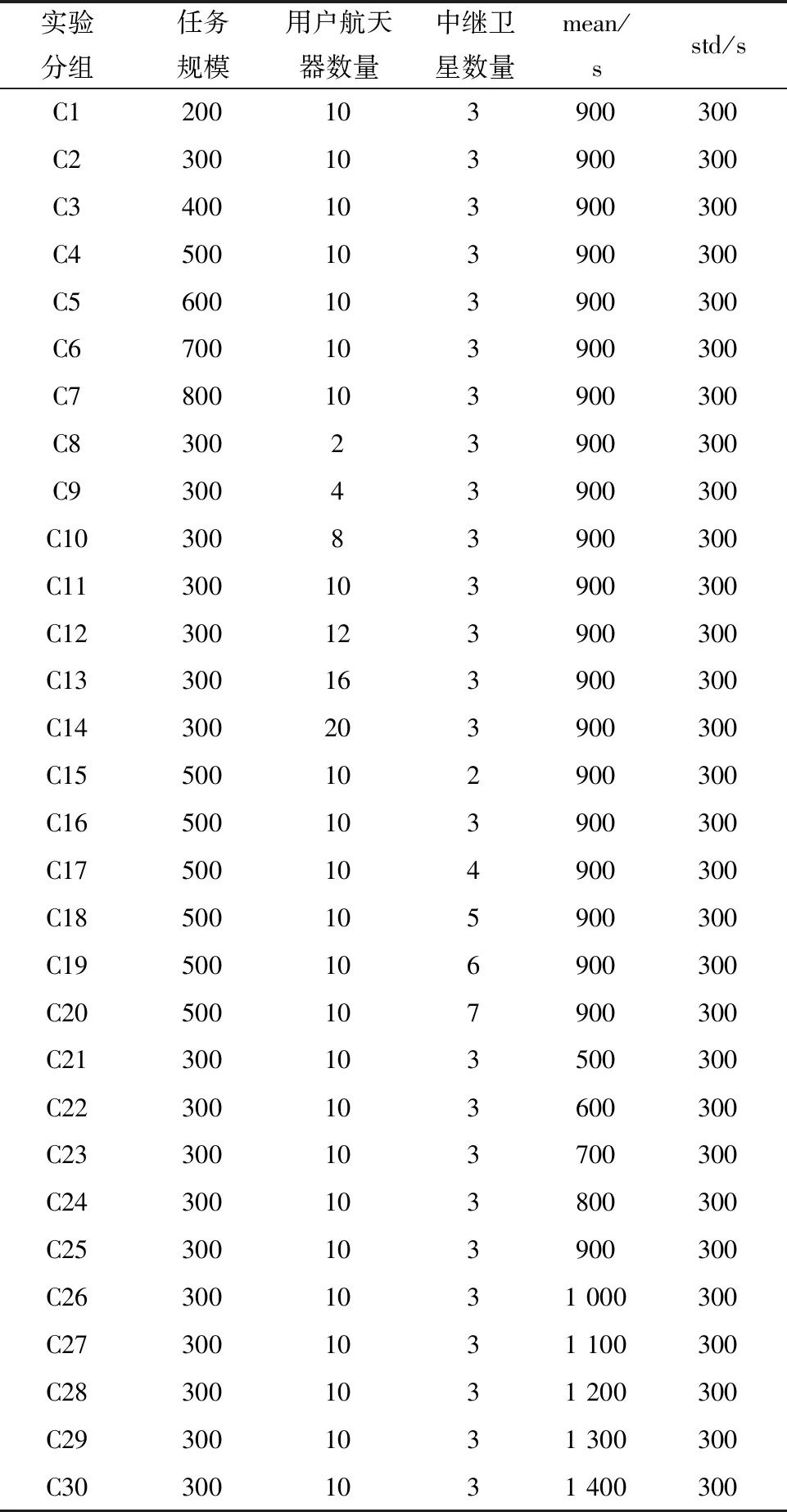
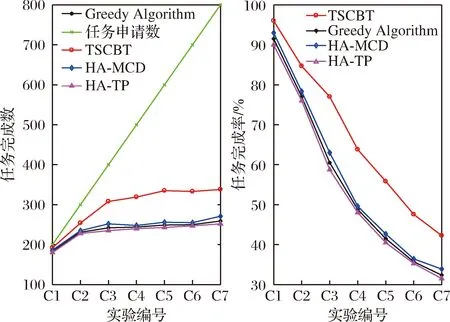

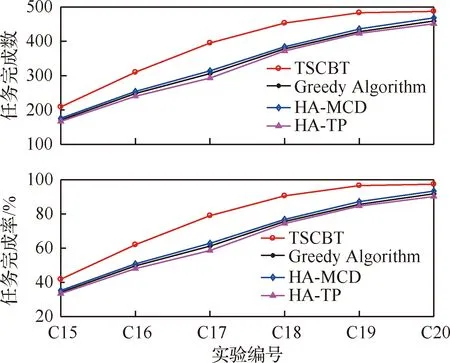


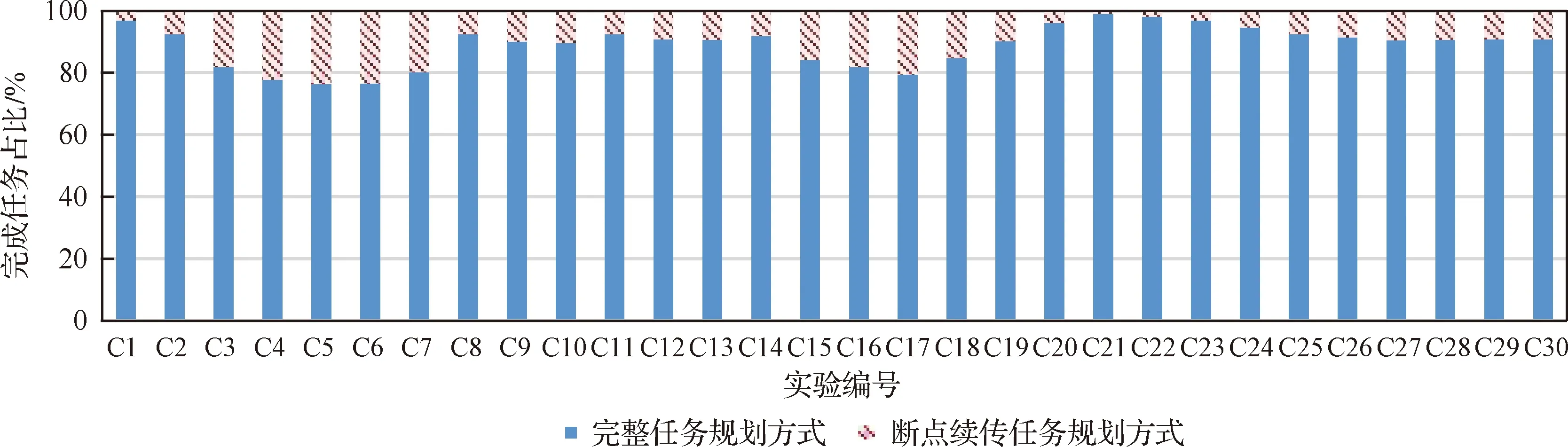
Table 7 Algorithm performance test results for different number of tasks

4 结 论

