基于多目标优化的飞防队作业调度模型研究
曹光乔 张庆凯, 陈 聪 张 萌 张进龙 黄玉祥
(1.农业农村部南京农业机械化研究所, 南京 210014; 2.西北农林科技大学机械与电子工程学院, 陕西杨凌 712100)
0 引言
近年来,无人机植保技术凭借其作业效率高、成本低等特点,发展极为迅速,国内植保无人机保有量及作业面积逐年大幅增长[1-5]。但是,农机社会化组织服务能力弱,农机主管部门对植保飞防队缺乏有效调度手段,限制了无人机植保技术的进一步推广[6]。鉴于病虫害防治的强时效性以及有限的无人机资源,建立高效的智能调度模式对于提高病虫害防治效率、降低作业成本具有重要意义。
目前,国内外对于农业领域的无人机调度研究相对较少,现有研究多集中于农田内的航线规划[7-9],相关农机调度的研究多集中于作物收获环节。在不同作业场景下,各调度模型所考虑的变量及约束条件是其主要差异。张璠等[10-11]建立了适用于机主选择的农机调配模型,以作业收益最大作为优化目标,应用基于启发式优先级规则的农机调配算法进行求解,随后针对农机应急调度场景,提出了两种基于优先策略的紧急调配算法,对以作业损失和调度成本为优化目标的调度模型进行了解算。吴才聪等[12]提出带时间窗的多目标农机调度模型,并利用动态规划的思想对模型进行了求解。EDWARDS等[13]提出了考虑农田作业条件的农机调度模型,并利用改进的禁忌搜索算法进行求解,该模型适用于多作业环节顺序执行的场景。THUANKAEWSING等[14]以产量最高为优化目标,提出了甘蔗收获机调度模型,该模型以各农田产量最高时段的收获比例作为约束。HE等[15]建立了以作业总时间为优化目标的调度模型,将各收获机收获时间差异作为约束,且考虑了不同机型、农田土壤类型对于调度的影响。与农作物收获等作业环节相比,植保作业周期更短,且农田病虫害爆发具有随机性,各个农田侵染状况也存在差异。因此,现有农机调度模型及算法不能直接应用于飞防队作业调度问题。现有研究表明,农机资源调配属于多目标优化问题[12,16],但目前研究多将农机资源调度问题转化为单目标优化问题进行求解[10, 12]。
本文以面向订单的多飞防队协同作业模式为对象,对植保飞防队调度模式进行分析,建立多目标飞防队作业调度模型,并提出订单优先级排序算法和基于NSGA-Ⅱ的作业路径规划算法,旨在提出合理的飞防队调配方案,以提高农机的利用效率和作业效益。
1 作业调度模型的建立
1.1 调度模式分析
当前,农机服务公司或农机合作社拥有的无人机数量多,是无人机植保社会化服务的主力军[17]。但受成员文化水平及技术的限制,无人机作业管理智能化水平较低,传统的人工调度经验难于满足复杂的植保作业需求。
为适应订单式、托管式、统防统治等农田作业模式,植保飞防队的作业调度需要解决多个作业订单的作业排序、作业时间安排、飞防队作业路径规划等问题。飞防队调度问题的关键在于无人机资源与订单信息的协同整合,生成最优的作业方案。在病虫害防治作业季,农户通常需预先向农机服务公司或合作社提交订单信息,通常包括作业时间窗、作业面积信息、作业价格、作业位置、农田病虫害侵染情况;调度中心通过管理端,对植保无人机位置信息、种类、作业效率等信息进行汇总;农机服务公司或合作社根据汇总的订单信息,参照历史调度经验和策略制定出调配方案,并组织飞防队按调配方案的转移路径和时间实施作业。飞防队作业调度问题属于多目标优化问题,在满足作业质量情况下,植保服务收益是各经营主体优先考虑的目标,同时更短时间完成所有订单,可以降低病虫害造成的作物产量和品质损失。因此,本文的调度目标为在满足各项约束的情况下总收益最大、作业总时长最小。
结合农业生产需求以及复杂的农田环境,本文研究基于以下假设:①在作业过程中,作业质量不随调度方案发生变化。②一个飞防队拥有一台植保无人机,若干工作人员,由车辆运载转移。③无人机作业效率恒定且作业过程中无故障。④飞防队每日可工作时长固定,开展防治作业和田间转移,其余时间为非作业时间。⑤一个飞防队可响应多个订单,一个订单亦可由多个飞防队完成,多个飞防队协同作业时,到达目标农田的时间可不同,当全部作业完成后可同时离开。⑥单个飞防队的转移路径以初始合作社位置为起点,以最后完成的订单位置为终点。⑦飞防队在订单时间窗前到达目标农田,需等待至作业订单时间窗下限方能开始作业,作业结束时间不得超过订单时间窗上限。
1.2 相关影响因素数学形式表达
(1)定义集合M={m1,m2,…,mm}表示m组无人机飞防队,每个飞防队可以表示为
mi={{xi,yi},w,v,C}
(1)
其中{xi,yi}为飞防队i的经纬度位置信息;w为飞防队生产率;v为飞防队的转移速度。C={cs,cw,ct,cd}表示飞防队作业中所产生的各项收入和成本。cs为植保无人机单位面积作业收费;cw为植保无人机单位面积的使用成本,包含机具折旧、飞防队人工费用和动力费用等;ct为飞防队单位距离的转移成本,主要为车辆燃油消耗和驾驶员人工费用;cd为飞防队单位等待时间的成本。
(2)定义集合O={o1,o2,…,on}表示n个农田订单作业信息集,单个订单信息为oj={{xj,yj},Aj,{Tsj,Tej},lj}。其中{xj,yj}为订单j的经纬度位置信息;Aj为订单j的农田作业面积;{Tsj,Tej}为订单j的时间窗,Tsj为计划开始作业时间,Tej为最晚结束作业时间;lj为农田侵染状况,其影响订单优先级顺序。
(3)定义集合Pr={Vp,dgh}表示路网中各路径节点及路径信息,其中Vp=Vf∪Vm。Vf={Vf1,Vf2,…,Vfm}为农田节点集合;Vm={Vm1,Vm2,…,Vmn} 为各飞防队初始位置节点集合;dgh为节点g、h之间的距离。
(4)定义集合Ma={pi(g,h),xij}为相关标志位符号。其中pi(g,h)为路径转移标志位,g∈Vf∪Vm,h∈Vf∪Vm, 若飞防队i经过节点g到达节点h则pi(g,h)为1,否则为0;xij为作业标志位,若飞防队i在农田j作业则xij为1,否则为0。
(5)定义Tz={ti(g,h),taij,tsij,teij,Tr}为相关时间的集合。其中ti(g,h)为飞防队i在点g、h之间转移所消耗的时间;taij为飞防队i到达农田j的时间;tsij为飞防队i在农田j的实际开始作业时间;teij为飞防队i在农田j的实际完成作业时间;Tr为整个作业进程中的非作业时间总和。
1.3 作业调度数学模型
1.3.1目标函数
(1) 作业总收益最大化

(2)
式中F——所有农机作业的总收益,元
农机作业的总收益等于作业的总收入减去总成本。作业总成本包括无人机使用成本、飞防队等待时间成本以及飞防队转移成本。其中无人机使用总成本等于单位面积的使用成本与总作业面积的乘积,等待时间总成本等于单位等待时间成本与所有飞防队各任务总等待时长的乘积,转移成本等于所有飞防队转移总路程与单位路程转移成本的乘积。其中等待时间成本及转移成本为调度相关成本,通过合理的调度方案可降低成本。
(2)作业总时长最小化
minT=maxteij-mintsij-Tr
(3)
式中T——作业总时长,h
作业总时长为最早一个订单的实际开始作业时间与最后一个订单的实际完成作业时间之间的时长,减去整个作业进程中总的非作业时间。
1.3.2约束条件
通过对无人机飞防队调度过程的分析,确定主要约束条件为
(4)
(5)
(6)
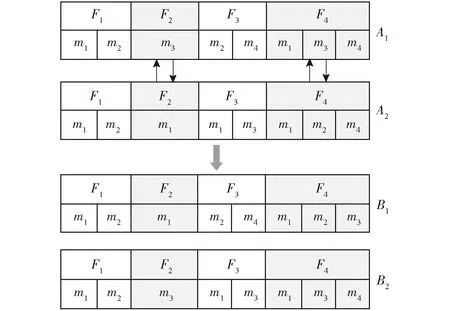
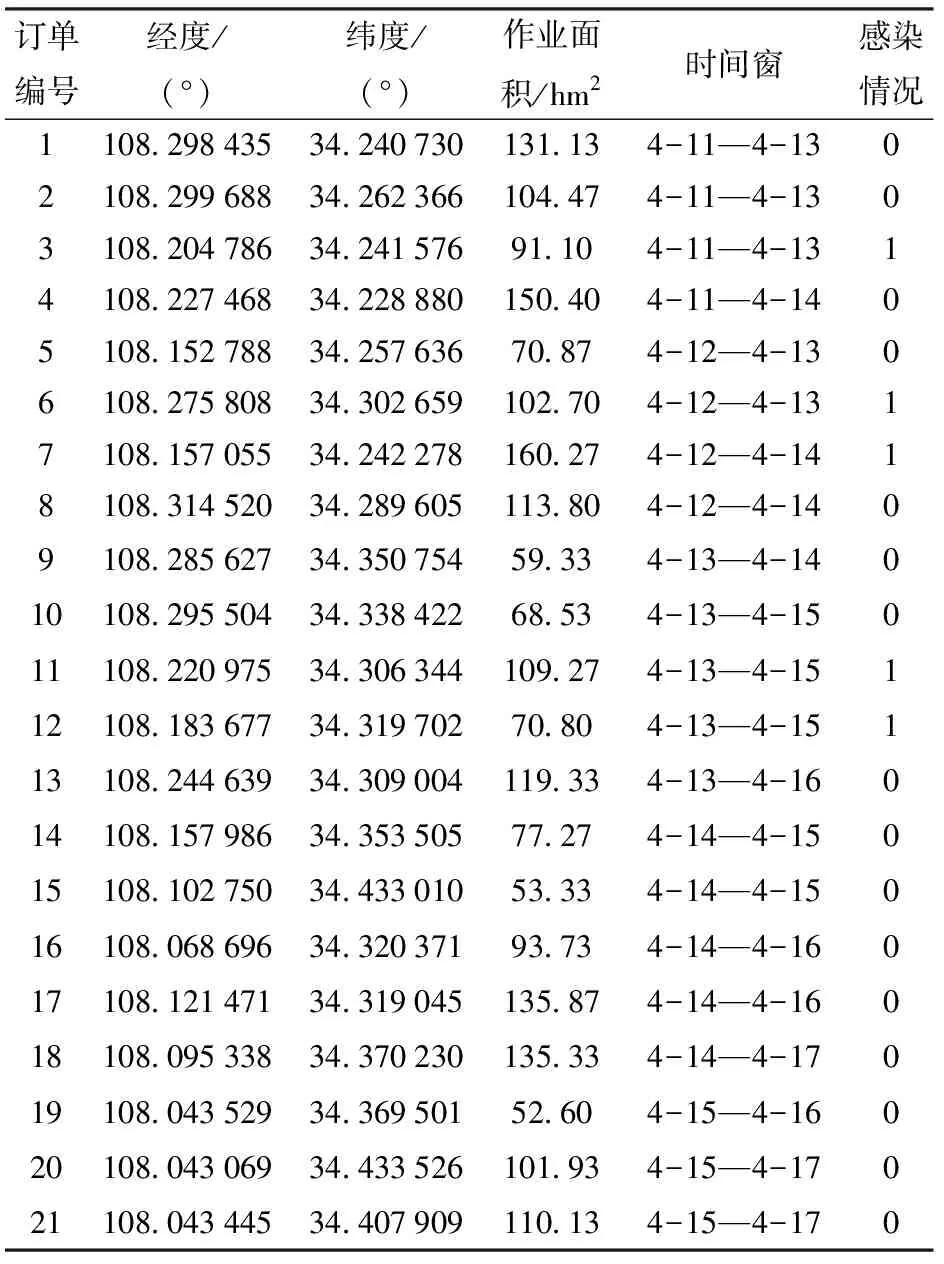
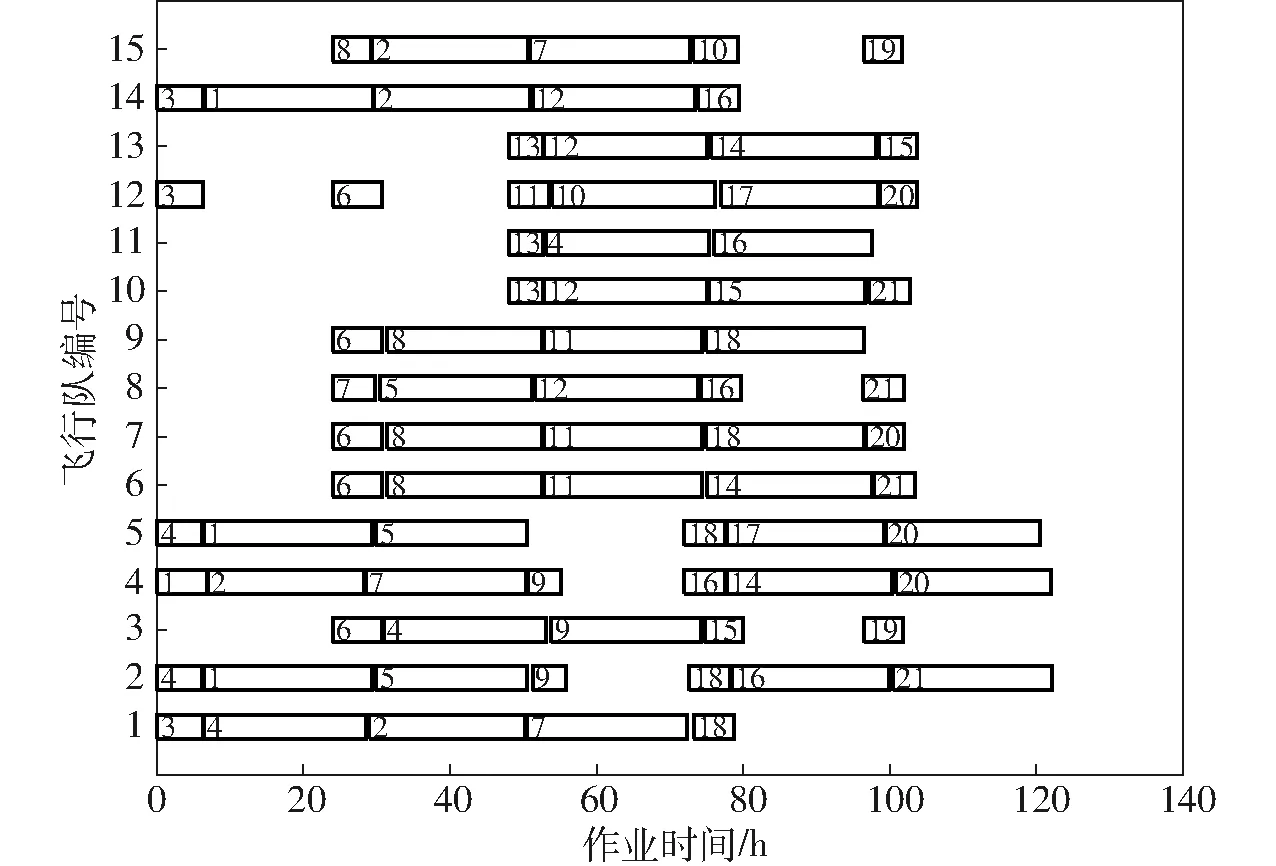
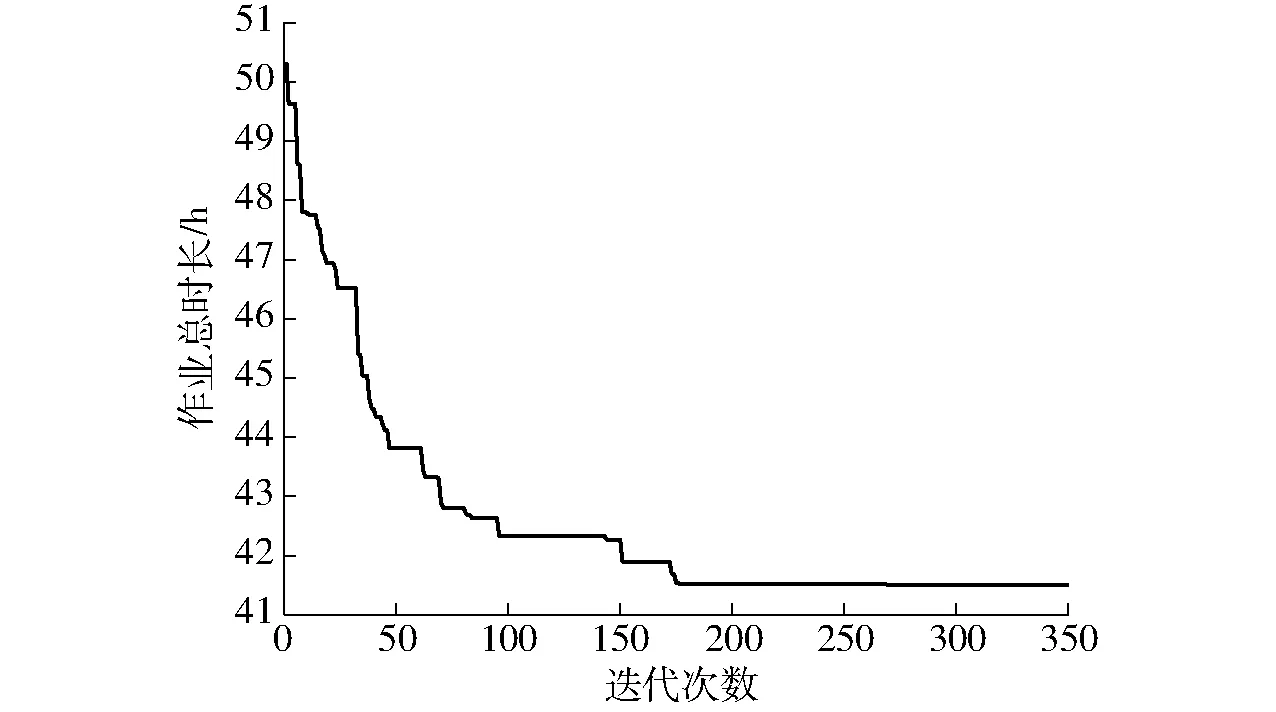
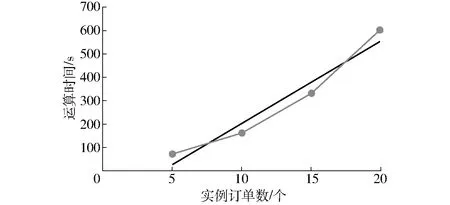
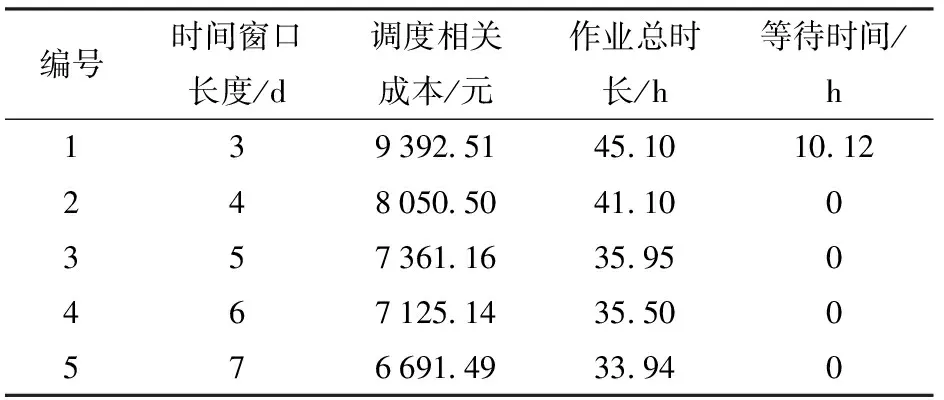
tsij (7) (8) 式(4)表示所有订单均有飞防队进行服务;式(5)~(7)为订单作业时间的相关约束,式(5)表示飞防队i经作业点g到达点h的时间等于离开点g的时间加上路程转移时间;式(6)表示飞防队i在订单g的实际完成作业时间等于飞防队i在点g的实际开始作业时间加上在点g作业的时间;式(7)表示订单的硬时间窗约束,订单的实际完成时间不得晚于订单时间窗要求;式(8)表示进入农田的飞防队和离开农田的飞防队数目相等。 飞防队作业调度算法应能为各农田订单分配合适的飞防队,同时为飞防队规划合理的转移路线,该调度方案需同时满足总收益最大、作业总时长最小两个优化目标,因此飞防队作业调度问题属于多目标优化问题。大多数情况下多目标优化问题不存在同时满足所有目标最优的解,各优化目标之间会相互冲突,只能协调各优化目标,最优解并不唯一,而是Paroto解集,需由决策者进行均衡[18-20]。针对此类复杂的优化问题,传统的方法如线性加权法、约束法等往往将多目标转化为单目标进行处理,但目标权重难以确定[21-22]。目前用于求解多目标优化问题Paroto解集的算法有:遗传算法[23-24]、禁忌搜索算法[25-26]、粒子群算法[27]、蚁群算法[28-29]等。其中Deb提出的带精英策略的非支配性排序的遗传算法(NSGA-Ⅱ)因具有良好的分布性和较快的收敛速度,被广泛应用于各类优化问题分析。本文考虑病虫害防治需求及算法求解效率,设计了考虑病虫害程度的作业排序算法和基于NSGA-Ⅱ的作业路径规划算法,分两步对飞防队作业调度模型进行求解。 病虫害防治具有强时效性,本文所设计的目标函数以及约束也与各订单的作业顺序紧密相关。在调度时,按照一定的优先级规则对订单进行排序,然后按次序进行调度作业,可获得较好的优化目标函数值,且更适应病虫害防治的实际需要。 2.1.1影响排序的相关因素 (1)病虫害侵染状况 现有研究较少涉及病虫害防治的适时性损失,较难将病虫害的爆发风险或经济损失引入调度模型,但经验表明对病虫害严重的订单优先作业,可有效降低病虫害扩散风险及经济损失。因此,本文将病虫害侵染状况作为订单作业排序的关键因素。农户在提交订单时,可按照常规观测方法,将作业订单的病虫害等级,设置为重度、中度和轻度3个等级。 (2)时间窗 农户可根据以往病虫害爆发规律、当年气候情况、病虫害扩散趋势和速度等,设置订单作业时间窗。在订单优先级排序时,订单要求的计划开始作业时间越早,时间窗长度越短,订单的优先级越高。 (3)作业面积 农业病虫害具有扩散性,对连片面积较大的订单优先作业,可以获得良好的防治效果,亦更能发挥无人机高效作业的优势。因此,农户订单作业面积越大,订单优先级越高。 2.1.2算法设计 本文所设计的订单作业排序算法分为组间排序与组内排序两个步骤。首先按照农田侵染状况对订单进行分组,然后按照订单时间窗和作业面积的优先级函数进行组内排序,该优先级函数为 p=w1Aj+w2Tsj+w3bj (9) 其中 bj=Tej-Tsj (10) 式中bj——订单j的时间窗长度,d w1——变量Aj在优先级函数中的权重 w2——变量Tsj在优先级函数中的权重 w3——变量bj在优先级函数中的权重 在计算时考虑到量纲的统一,式(9)中Aj、Tsj、bj均进行归一化处理,并有w1+w2+w3=1,各变量权重可根据实际调度需求进行调整。 综上所述,作业排序算法步骤如下: (1)取出农田作业订单集O,并建立3个订单类别子集O1、O2、O3。 (2)将所有设置为重度病虫害的农田订单添加至O1,设置为中度病虫害的农田订单添加至O2,其余订单添加至O3。 (3)在O1、O2、O3内分别计算每个订单ok的优先值pk,并按照pk大小将订单排序。 (4)将O1、O2、O3依次连接,对所有订单重新编号,完成农田作业订单集O优先级排序。 2.2.1染色体编码 染色体编码是遗传算法成功实施优化的关键。结合上文排序算法的设计,此处采用双层编码的编码方式,如图1所示。 图1 编码方式Fig.1 Coding mode 第1层为农田编码,第2层为飞防队编码,图1中第1层编码为农田F1~F4,第2层中各元素代表在上层农田中作业的飞防队编号,如在F1订单中作业的飞防队为m1、m2,同一订单中的飞防队编号不分先后顺序。 2.2.2基于贪婪思想的种群初始化 传统的遗传算法中的初始种群多通过随机生成的方法构建,对于飞防队调度问题可能会产生大量的劣质解或非法解。为避免无效解的生成以及提高算法的运算效率,本文采取以下方法产生初始种群。 定义:设Tc(i,j)为飞防队i到达农田j时的适时度,Tc(i,j)越小,适时度越高,其中 Tc(i,j)=|Tsj-taij| (11) 为农田选择适时度高的飞防队,可获得较好的两目标函数值,种群初始化流程如下: (1)导入完成排序的农田订单集O,以及飞防队集M,设置i=j=1。 (2)判断O是否为空,若为空则跳转至步骤(6),否则顺序执行。 (3)依序取出订单oj,按照公式计算所有飞防队相对于订单oj的Tc(i,j),并按照Tc(i,j)由小到大的次序将飞防队m排序。 (4)取出Tc(i,j)值最小的飞防队mi分配给oj。 (6)整理工作表,结束。 2.2.3模型约束的处理 考虑到本文使用的时间窗为单边硬时间窗,若直接采用所建模型的目标函数构建适应度函数,在进化过程中会产生较多无效解。为保证种群数量,本文采用罚函数法对时间窗约束进行处理,即通过给超出订单最晚作业时间的解的目标函数一定的惩罚值,以降低不可行解进行遗传操作的概率,可达到降低不可行解在种群中的比例[30]。在算法中需对优化目标添加惩罚项,式(3)则变为 (12) 2.2.4遗传算子 (1)选择算子 普通遗传算法可利用目标函数所构造的适应度函数进行父代种群的选取,NSGA-Ⅱ从第2代起则需将子代种群与父代种群合并,根据各染色体之间的非支配性关系,同一层级个体之间的拥挤度,选取父代种群进行杂交和变异操作。本文使用标准的快速非支配性排序算法和拥挤度计算算法。 (2)交叉算子 交叉算子影响遗传算法在解空间中的搜索能力,对于遗传算法达到全局最优起着关键作用[31]。 若对本文所设计的编码结构进行常规交叉操作,必然会出现大量非法解,增加算法的复杂度,因此本文采用变异的部分映射交叉算子(Partially mapped crossover,PMX)对所选择的父代个体进行交叉操作,以提高可行解的比例。基本操作为:在一层农田编码中随机产生两个交叉点,即交叉点 1 和 2,将两父代个体A1、A2的对应交叉点下层基因对应交换,生成新个体B1、B2。以含4个农田以及4个飞防队编码的染色体为例,F2、F4农田下的飞防队发生交叉,交叉过程如图2所示。 图2 染色体交叉过程Fig.2 Chromosome crossing process (3)变异算子 变异操作是保证种群多样性的重要手段,本文变异算子的基本操作为:在选中个体农田编码中随机产生1个变异点,对该农田编码下层农机编码片段进行随机变异,生成新个体,规定至少有一个农机编码片段发生变异,同样以含4个农田以及4个飞防队编码的染色体为例,F3农田中的m3号农机位发生变异,变异过程如图3所示。 图3 基因变异过程Fig.3 Gene mutation process 2.2.5整体算法步骤 基于NSGA-Ⅱ算法的飞防队调度算法运行流程如下: (1)读取完成排序的农田作业订单集O及飞防队集M,初始化路径节点实际行车距离矩阵D。 (2) 设置最大迭代次数gen,种群规模Size,交叉概率Pc,变异概率Pm,迭代次数i=1。 (3)按照初始解生成算法构建初始解,随机变异产生初始种群P0=(x1,x2,…,xn)。 (4)若满足i>gen,则输出当前最优Paroto解集Xi,绘制相关图表,结束程序;否则跳转至步骤(5)。 (5)按照交叉概率Pc选取进行交叉的父代个体,使用PMX算子对父代个体进行交叉操作。 (6)按照变异概率Pm选取进行变异的个体,对其中的农机编码片段进行变异操作,得到子代种群Si。 (7)将父代种群Pi-1与子代种群Si合并,构成新的规模为2Size的种群ConX,计算ConX中个体对应的作业总收益和作业总时间,并进行非支配性排序,并计算同支配序列拥挤度。 (8)将种群规模恢复为Size。若ConX中非支配序列为1的个体数大于种群规模Size,则选择拥挤度较小的个体进入新的父代种群Pi;若数量小于Size,将ConX中非支配序列为1的个体复制到Pi;对非支配序列为2及以上的个体随机进行两两比较,根据非支配等级和拥挤度选取进入种群Pi的个体,直至种群规模恢复为Size。 (9)记录当前种群Pi全局最优Paroto解集为Xi,i=i+1,跳转至步骤(4)。 以陕西省武功县小麦“一喷三防”作业为例进行实验验证。该项作业需要调度武功县及周边乾县和兴平县等3个合作社的15支飞防队,为21个基层村的小麦植保提供统防统治作业,作业时限为7 d。基层村历史订单信息通过陕西省某植保无人机调度中心信息管理平台获取,飞防队实际作业能力及各项成本信息通过调研合作社获取,各路径节点信息及实际行车距离由天地图API获取。具体作业订单信息、无人机植保飞防队信息、其他要素信息等如表1~3所示。 在IntelCorei5 CPU 3.0 GHz、内存为8.0 GB、操作系统为Windows 10的个人计算机上采用Matlab R2018a软件编程实现本文所设计的作业优先级排序算法及飞防队作业路径规划算法。实验中设置算法的相关参数为:种群规模200,最大进化代数350,交叉率0.8,变异率0.1。 通过代入实例数据,算法可求出一个Pareto最优解集,能获得各优化目标下的非支配解。表4为上文算例运行一次后的实验结果,Pareto最优解集中包括3个调度方案,各个方案中的优化目标值如表4所示,所有订单均能完成作业,同时满足单边时间窗的约束。 图4为获得最大作业总收益时的各飞防队调度甘特图,图内条块表示每个飞防队的作业计划,包括作业订单编号、作业开始时间、作业结束时间。 通过本文所设计的算法可得到每个合作社每个飞防队的转移路线。以2号农机合作社为例,图5为4个飞防队的作业转移路线图,其中农机合作社及农田位置由经纬度坐标点给出。 由图可直观看出,每个无人机所分配到的作业任务之间具有空间上的邻近性,表明了实验结果的合理性。 表1 农田作业订单信息Tab.1 Information for each job order 注:感染情况随机生成,0表示为轻度病虫害,1为中度病虫害。 表2 合作社飞防队信息Tab.2 UAV plant protection team informations of cooperatives 表3 其他相关作业信息Tab.3 Other relevant working information 注:此处作业成本仅包括机器折旧、人工成本等,不含药剂费用。 表4 Pareto最优解集目标值Tab.4 Pareto optimal solution set 图4 调度甘特图Fig.4 Scheduling Gantt chart 图5 无人机飞防队转移路线Fig.5 Roadmap of UAV teams transfer 在实际应用中,决策者可针对生产需要,从Pareto最优解集中选择最佳作业方案。 图6为Pareto解集在调度相关成本-作业总时长空间的分布情况,非支配解集中的各解相对分散,可知算法可在解空间中实现有效搜索。 图6 非支配解的分布情况Fig.6 Distribution of non-dominated solutions 运行过程中的各目标函数最优值的变化情况如图7、8所示,调度相关成本、作业总时长随迭代次数的增加而降低,且在迭代次数增加至200次左右即可收敛至稳定值。计算结果表明该算法可实现稳定收敛并具有较好的搜索性能。 图7 调度相关成本随迭代过程的变化曲线Fig.7 Changing curve of scheduling related cost with iteration process 图8 作业总时长随迭代次数的变化曲线Fig.8 Changing curve of total time of operations varied with iterative process 图9 运算时间随订单数的变化曲线Fig.9 Changing curves of operating time of each case 调研数据表明,在单次防治作业任务中,合作社收到村级订单数量一般不超过20个,单个订单作业量33.33~200.00 hm2。在实例数据中分别挑选5、10、15、20个订单数据组成4个算例,运行本文设计的飞防队调度算法,记录两目标函数值优化至稳定值时所花费的时间,如图9所示,运算时间随订单数量的增加而增大,且近似线性增长。当算例订单数量达到20个时,订单作业总面积1 976.30 hm2,运算时间为613 s,基本满足实际调度需求。在进一步的研究中,可结合其他启发式搜索策略以提高运算效率,同时通过对订单任务进行合理合并,也可降低问题规模,减少运算时间。 同时,在县域范围内,病虫害防治单次作业合理周期约为7 d左右,订单作业窗口可由农户根据实际需要以及提交订单的先后顺序进行排定。为探究时间窗长度的变化对调度结果的影响,本文设计了以下实验进行验证。 针对上述实例,保持其他数据不变,分别设置所有订单时间窗长度为3~5 d,在每个时间窗长度水平下使用本文算法分别进行5次仿真,可得时间窗长度与调度相关成本和作业总时长的关系,仿真结果如表5所示。 表5 时间窗口长度对实验结果的影响Tab.5 Effect of time window duration on experimental results 注:各项结果为5次实验的平均值。 由表5可知,在总作业周期不变的情况下,当订单时间窗口长度大于3 d时,等待时间成本消失,调度相关成本仅为转移成本,且随时间窗长度的增加,调度相关成本与作业总时长均呈下降趋势。 当总作业周期固定时,订单时间窗口越长,各订单的时间窗口重叠度增加,时间窗对飞防队作业调度的约束会降低,不需要为满足部分订单的时间窗要求而增加飞防队的转移距离;同时订单时间窗重叠度的增加,降低了因订单时间窗过于集中或分散造成飞防队不能满足订单作业需求或飞防队等待作业时间过长的风险,提高了无人机利用效率。 因此,在实际生产中,飞防队可鼓励无急迫作业需求的农户,设置较大的订单时间窗长度,以降低作业总成本和作业总时长,实现更高效合理的调度。 (1)以面向订单的多飞防队协同调度为研究对象,对飞防队作业调度的各项成本进行分析,构建了以调度总收益最大和调度总时长最小为优化目标的飞防队作业调度模型。该模型考虑了农田面积、无人机和农田位置信息、作业时间窗等因素,满足多目标调度需求以及单边硬时间窗的约束,提高了飞防队作业调度模型的准确性。 (2)通过分析对比多目标调度算法特点,结合飞防队作业调度需求,提出了考虑病虫害侵染状况的作业优先级排序算法和基于NSGA-Ⅱ的作业路径规划算法,并对飞防队作业调度模型进行了求解。 (3)通过Matlab软件进行了算例及算法运行相关实验分析,本文提出的飞防队作业调度模型及算法,求解出满足时间窗约束的Pareto解集,为决策者提供了多个备选的调度方案。2 作业调度算法设计
2.1 考虑病虫害侵染状况的订单优先级排序算法
2.2 基于NSGA-Ⅱ的作业路径规划算法



3 实例分析
3.1 算例
3.2 算法运行结果分析






4 结论

